A reaction density functional theory study of solvent effect in the nucleophilic addition reactions in aqueous solution

Cheng Ci,Weiqing Tng,Chongzhi Qio,Bo Bo,Peng Xie,Shungling Zho,,Hongli Liu

a State Key Laboratory of Chemical Engineering and School of Chemical Engineering,East China University of Science and Technology,Shanghai,200237,China

b School of Chemistry and Molecular Engineering,East China University of Science and Technology,Shanghai,200237,China

c Guangxi Key Laboratory of Petrochemical Resource Processing and Process Intensification Technology,School of Chemistry and Chemical Engineering,Guangxi University,Nanning,530004,China

Abstract Whereas the proper choice of reaction solvent constitutes the cornerstone of the green solvent concept,solvent effects on chemical reactions are not mechanistically well understood due to the lack of feasible molecular models.Herein,by taking the case study of nucleophilic addition reaction in aqueous solution,we extend the proposed multiscale reaction density functional theory(RxDFT)method to investigate the intrinsic free energy profile and total free energy profile,and study the solvent effect on the activation and reaction free energy for the nucleophilic addition reactions of hydroxide anion with methanal and carbon dioxide in aqueous solution.The predictions of the free energy profile in aqueous solution for these two nucleophilic addition reactions from RxDFT have a satisfactory agreement with the results from the RISM and MD-FEP simulation.Meanwhile,the solvent effect is successfully addressed by examining the difference of the free energy profile between the gas phase and aqueous phase.In addition,we investigate the solvent effect on the reactions occurred near solid-liquid interfaces.It is shown that the activation free energy is significantly depressed when reaction takes place in the region within 10 Å distance to the substrate surface owing to the decrease of hydration free energy at the solid-liquid interface.

Keywords: Reaction density functional theory;Nucleophilic addition;Solvent effect;Charge models

1.Introduction

Against the backdrop of growing concerns about the global crisis of chemical pollution and resource depletion,green chemistry has been proposed.The development of green chemistry aims to solve the environmental impact of chemistry,including reducing consumption of nonrenewable resources and technological approaches for preventing pollution[1-4].For guiding the practice of green chemistry,a set of principles was recently published by Anastas and Warner [5].The principles cover the following concepts as preventing waste [6],atom economy [7,8],catalysis,safer solvents and auxiliaries [9],design for energy efficiency [10] and so on.The realization of these concepts essentially lies on the improvement of reaction selectivity and efficiency,which,to a great extent,depends on the proper setup of reaction condition such as reaction solvent,catalyst,and reactor,etc.Indeed,in many liquid-phase reactions,the energy profiles including reaction free energy and activation free energy are very sensitive to the type of liquid solvent [11].The influence of solvent surroundings to chemical reactions,conventionally termed as solvent effect [12],has become a control step in chemical engineering and organic chemistry,and attracted widespread interests from both engineers and scientists.

In recent years,significant progresses have been made towards the manipulation of solvent effect [13-15].In addition to traditional chemical solvents [16],ionic liquids and supercritical fluids are regarded as promising media for enhancing chemical reactions.Prior researches on ionic liquids show that they have great potential for developing green processes of renewable energy [17],such as the convention of carbon dioxide to fuels and fuel additives [18,19],the pretreatment of biomass and its conversion to biofuels and chemicals [20].Supercritical fluids such as supercritical carbon dioxide have been widely used in polymerization reactions [21] and asymmetric catalytic hydrogenation reactions [22] since reactants in supercritical carbon dioxide have gas-like diffusivities and excellent solubility.

Despite these inspiring progresses,the solvent effects on chemical reactions are not yet mechanistically well understood.This is mainly due to the lack of feasible molecular models.Till date,several theoretical approaches have been proposed to investigate solvent effect including quantum mechanical molecular mechanical (QM/MM) [23,24],extended reference interaction site model (RISM) [25],ab-initio molecular dynamics (AIMD) [26,27],polarizable continuum models [28] and so on.These approaches are either computationally expensive and inconvenient,or not sufficiently accurate.Recently,we proposed a multiscale reaction density functional theory (RxDFT),which employs quantum density functional theory for dealing with intrinsic chemical reaction coupled with classical density functional theory for addressing solvent effect.This multiscale method has been successfully demonstrated to describe the free energy profile and address the solvent effects for the symmetric and asymmetric nucleophilic substitution (SN2) reactions in aqueous solution [29]and in acetonitrile [30].In addition,we also obtained the free energy profiles of a glycine tautomerization reaction and a derivative of 1,3,4-oxadiazole tautomerization reaction in aqueous solution [31].

Herein,to further unravel solvent effect,we extend the RxDFT to investigate the nucleophilic addition reaction of hydroxide anion nucleophilic attack on methanal and carbon dioxide in aqueous solution.The nucleophilic addition of hydroxide anion to carbonyl group is one of the most fundamental and valuable reactions,and it is widely used in organic chemistry and biology.In living systems,the nucleophilic addition reaction of hydroxide anion with carbon dioxide plays an important biological role in the transportation of carbon dioxide and blood pH regulation [32,33].Jonsson et al.[34]and Liang et al.[35]carried theoretical studies and they found that there is no reaction barrier on the gas-phase energy profile.However,experimental works showed that there is an apparent activation energy barrier of 13.25 kcal mol-1in aqueous solution [36].On this deviation,Miertuˇs et al.gave a qualitative explanation based on a continuum solvent model [37].Later on,Peng and Merz [38,39]performed quantitative calculations,and they obtained the minimum energy path(MEP)in the gas-phase by using highlevel ab-initio calculations (up to MP4/6-311++G(d,p)),and the free energy profile in aqueous solution by using molecular dynamics free energy perturbation (MD-FEP) simulations.The calculated activation free energy in aqueous solution was evaluated to be 17 ± 2 kcal mol-1,rather close to the experimental data.Recently,ab-initio molecular dynamics(AIMD) [40] and cluster approach [41] were employed to investigate the free energy profile for this reaction in both the gas phase and aqueous solution,and the activation free energy was reported to be 9.7 kcal mol-1and 8.2 kcal mol-1,respectively.

The other prototypical nucleophilic addition reaction of hydroxide anion to the carbonyl group under consideration is OH-+HCHO →HOCH2O-.On this reaction,Jorgensen et al.performed comprehensive simulations in both the gas phase and aqueous solution by using a quantum and statistical mechanical method.In their simulation,a shallow ion-dipole minimum in the gas phase was determined by utilizing abinitio calculations at HF/6-31+G(d) level,and the activation free energy and reaction free energy in aqueous solution were 24-28 kcal mol-1and 10-14 kcal mol-1,respectively [42].The same reaction was examined by using an extended reference interaction site model(RISM)[25]integral equation method.This method gave similar calculation results,but required 2 orders of magnitude less computation time than the Jorgensen's calculation [43].

In this work,both reactions in aqueous solution are reexamined within the framework of RxDFT.As many chemical reactions occur at solid-liquid or liquid-liquid interfaces,the substrate effect is usually coupled with solvent effect,causing complex influence on chemical reactions,which deserves careful theoretical attention.Herein,we further extend the RxDFT method to assess the complex solvent effect of OH-+HCHO reaction at solid-liquid interfaces and evaluate the combined effect from inhomogeneous solvent surrounding to the chemical reactions.The remainder of this work is organized as follows: the theoretical framework of RxDFT is presented in the next section,and the computational method and details are described in section III.In section IV,the calculation results and relative discussion are summarized.A brief conclusion is given in section V.

2.Theoretical framework of RxDFT

Within the theoretical framework of RxDFT [44],the reaction system can be divided into two parts: the intrinsic reaction subsystem and the solvent subsystem.The reaction free energy in solution,FR,sums up the individual contributions from these two subsystems:

where ERdenotes the intrinsic reaction free energy in solution,and ΔFsolrepresents the difference in solvation free energies of products and of reactants.Following our previous studies[29,31,44],these two contributions can be addressed by quantum DFT and classical DFT,respectively.

The solvation free energy describes the change in grand potential of the solvent system with and without the presence of the solute molecule [45],and it can be formulated as:

where ρ（r，Ω）is the density distribution of solvent,which depends on the position and orientation of the solvent molecule.Vext（r，Ω）is the external potential to the solvent molecules originated from the solute-solvent interaction.μ is the bulk chemical potential of solvent.V and T are the volume and absolute temperature of the solvent system,respectively.nbis the bulk number density of solvent.

For a given solvent system with the presence of a solute,the external potential can be determined using standard classical force field,and the solvation free energy together with the solvent density distribution at thermodynamic equilibrium can be determined by minimizing the functional of solvation free energy in eq.(2) [45,46],namely:

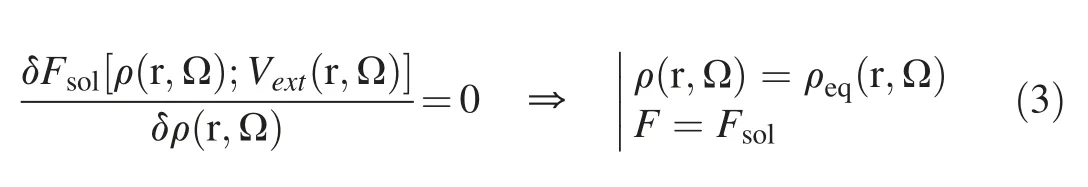
The detailed formulation and calculation of the solvation free energy are to be discussed below.

3.Computational methods and details

3.1.Intrinsic free energy calculation

The intrinsic reaction profile is carried out by using quantum DFT,and all the quantum calculations are performed with Gaussian 09 package program [47].Following the previous studies [38,39,42,43],the reaction coordinate (Rc) is defined as the distance between the oxygen atom of hydroxide ion with the carbon atom of carbon dioxide and methanal.Along the reaction coordinate,the geometries of the solute clusters,［HO…CH2O］-and ［HO…COO］-,are optimized in aqueous solution with the fixed values of Rc.All the constrained optimizations are calculated by using the Kohn-Sham DFT method at B3LYP/6-311++G(d,p) level [41] in aqueous solution with the SMD model [48,49] along the Cssymmetry axis.Meanwhile,the thermal corrections to Gibbs free energy at B3LYP/6-311++G(d,p) level are obtained.Next,single point frequency calculations of the optimized solute clusters are carried out at B2PLYPD3/def2-TZVP level[50]in the gas phase for calculating the intrinsic free energy,which sums up the thermal correction to Gibbs free energy and the singlepoint energy.The charge distribution is obtained with the same optimized geometries,and the details of the calculations will be discussed in the next subsection.

3.2.Solute–solvent interaction

To address the solvent effect and obtain the solvation free energy,a proper force field representation is required to accurately describe the interaction between the solute and solvent molecules.For a solute in aqueous solution,the external potential exerted on a water molecule with coordinate and orientation（r，Ω）contains Lennard-Jones and Coulombic contributions:

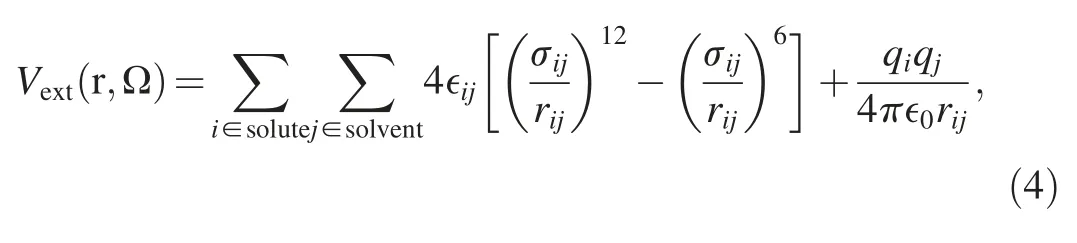
where rij,qiand qjdenote the interatomic distance and the charges on the i-th and j-th atoms,respectively.∈ijand σijare the cross-paired Lennard-Jones energy and size parameters,and are obtained from standard Lorentz-Berthelot combination rule: ∈ij=The Lennard-Jones parameters for individual atoms are obtained from the optimized potentials for liquid simulation all-atom(OPLS-AA) [51] force field.In equation (4),the Coulombic contributions totally depend on the charge distribution on solutes in solution,but the charge distribution on solutes may change during reaction process.Therefore,it is necessary to accurately describe the charge distribution of solute along the reaction coordinate [52].In quantum DFT calculations,there are many charge models to predict the charge distribution on solutes,and the predicted charge distribution may change with the reaction system.In this study,the polarity of the reactants(HCHO and CO2) is totally different,and thus would lead different behavior from the different charge models.To choose proper charge models for the OH-+HCHO reaction and the OH-+CO2reaction,several charge models are considered including Mulliken population analysis,Hirshfeld population analysis,charge model 5(CM5),M-K electrostatic potential fitting method,and natural population analysis (NPA).The computations of the charge distributions are performed with the B3LYP functional combined with the def2-TZVP basis set.

Before testing the charge models,only the intermolecular degrees of freedom between fixed solute and SPC/E water are optimized by using quantum DFT at B3LYP/6-31+G(d)level.Then,reference data of solute-solvent interaction are obtained from quantum DFT calculations at B2PLYPD3/def2-TZVP level by using optimized geometries of solute-water complexes,as shown in Fig.1.The Mulliken,Hirshfeld and CM5,M-K,and NPA charge models combining with OPLS/AA Lennard-Jones parameters for solute and the SPC/E model potential parameters for water molecule have been tested for their accuracy to reproduce the solute-solvent interactions.The correlations between the reference data and the interaction results for different types of solute-solvent interactions are shown below.

Fig.1.The optimized geometries of solute-water complexes for (a)［HO…CH2O］- cluster,Rc=2.0 Å;(b)［HO…COO］- cluster,Rc=2.0 Å.Rc is defined as the center-to-center distance between the carbon atom and the hydroxyl oxygen atom.

3.3.Solvation free energy calculation

With a given external potential,the grand potential of the solvent system can be expressed as:

where Fid［ρ（r，Ω）］ and Fexc［ρ（r，Ω）］ are the ideal free energy and excess free energy,respectively.After substituting eq.(5)into eq.(2) and carrying a few algebras,the solvation free energy functional can be formulated as [45,46]:

where Δρ（r，Ω）=ρ（r，Ω）-ρbwith ρb=nb／∫dΩ,and kBis the Boltzmann constant.c（2）（｜r-r′｜，Ω，Ω′）represents the orientation-dependent two-body direct correlation function(DCF) of the bulk water system,which can be extracted from standard molecular dynamics simulation,is prepared as an input in prior [53,54].FB［ρ（r，Ω）］,designated as bridge functional,accounts for the contribution from multi-body correlations,and following previous studies[45,46,55,56],it is assumed the repulsive interaction dominates the multi-body correlations,and thus the bridge functional can be approximated with the counterpart of the reference inhomogeneous hard-sphere system,namely:

Next,the minimization of eq.(3)gives the following Euler-Lagrange equation:

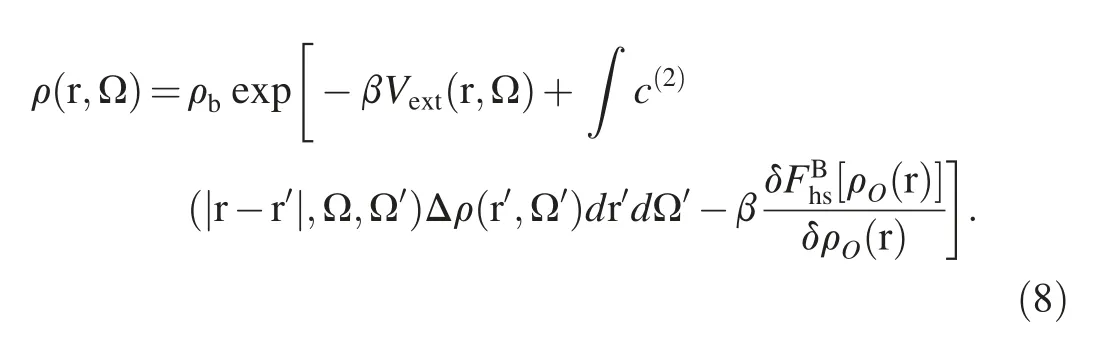
Technically,the solute is fixed at the center of a cubic grid box,and the inhomogeneous density of water molecule relative to the solute,i.e.,ρO（r）,is discretized onto the Nx×Ny×Nzposition grids with Nibeing the grid number in the i direction.To describe the spatial configuration of the water molecule,each position grid is associated with a few angular grids on which the orientation vector,Ω,is discretized.The orientation vector is composed of three Euler angles Ω=（θ，φ）.The cos θ and φ determine the dipole direction of a water molecule.The combination of position grids and angular grids gives the complete description of ρ（r，Ω）.

When calculating the interaction between the solute and water molecules,the positions of hydrogen atoms (sites)within each water molecule are needed.The position of hydrogen site j is computed as rj=r+R（Ω，φ）sj,where sjis the vector of the hydrogen site relative to the oxygen site at position r,and R（Ω，φ）is the rotation matrix with the angle φ describing the rotation of water molecule around the dipole direction [58,59].Herein,SPC/E water model is employed[60],and thus the vectors for both hydrogen sites,i.e.,sHand sH′are (0.8165,0,0.5774) and (-0.8165,0,0.5774),respectively[61].The external potential,Vext（r，Ω）,is averaged over the φ angle and stored in prior before the minimization procedure.

The system temperature is 298.15 K and the bulk water number density is nb=0.033 particles Å-3.The convolutions in eq.(8) is calculated by using fast Fourier transforms (FFT)[62],and the angular integral is performed with the Gauss-Legendre integral method with Ncosθ× Nφ=4 × 8.The box length varies slightly with the presence of different solutes,and typically it's 32～40 Å.The number of position grids is Nx×Ny×Nz=64×64×64.The minimization procedure is carried out with the help of the limited memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method [63].It is important to note that the calculation from the RxDFT method requires rather low computational cost,and typically the solvation free energy calculation for each reaction coordinate cost less than 0.5 h without parallelization.

4.Results and discussion

4.1.OH- nucleophilic attack on HCHO

Initially,we estimate the intrinsic free energy profile for the nucleophilic addition reaction of OH-nucleophilic attack on HCHO.The full reaction path in aqueous solution is determined by the constricted optimizations at B3LYP/6-311++G(d,p) level with the SMD model,and the thermal correction to Gibbs free energies,ΔGT,at the selected reaction coordinate is obtained.The single-point energies in the gas phase are calculated at the B2PLYPD3/def2-TZVP level using the optimized structures.Fig.2 shows the intrinsic free energy profile for the reaction of OH-+HCHO.

For getting reasonable solute-solvent interaction,several types of charge distributions are calculated for the optimized solute clusters at the fixed values of Rc.The optimized geometric parameters and the charge distributions from the Mulliken,Hirshfeld,CM5,M-K,NPA charge models for the selected solute clusters in aqueous solution are listed in Table S1 in theSupporting Information(SI).

As discussed above,the calculations for the solvation free energy require an accurate description of atomic charges for the solute clusters along the reaction coordinate.The selected five charge models are tested,and the test results are shown in Fig.3.

As shown in Fig.3,the solute-solvent interactions based on the M-K and NPA charge models are better than the others,which capture the results from quantum DFT calculations.To ensure the accuracy of the solvation free energy calculations,we further explore the water structure around solute clusters.The solute-solvent radial distribution functions (RDFs) of reactants,TS,and products are determined by using classical DFT based on M-K charge distributions.In Fig.4,the RDFs for the aqueous oxygen around carbon are given (the RDFs around carbonyl oxygen and hydroxyl oxygen are in SI),and the RDFs calculated by classical DFT are plotted against those obtained by MD simulations from ref.43.Despite the difference of the parameters for solute-solvent interactions,the vast majority of the predictions on the first peak positions and peak heights from RxDFT have a reasonable agreement with the results from MD simulation.Therefore,the solvation free energies are carried out by using classical DFT with the help of these two atomic charge models.

Fig.2.Intrinsic reaction energy profile along the reaction coordinate for the reaction of OH-+HCHO.

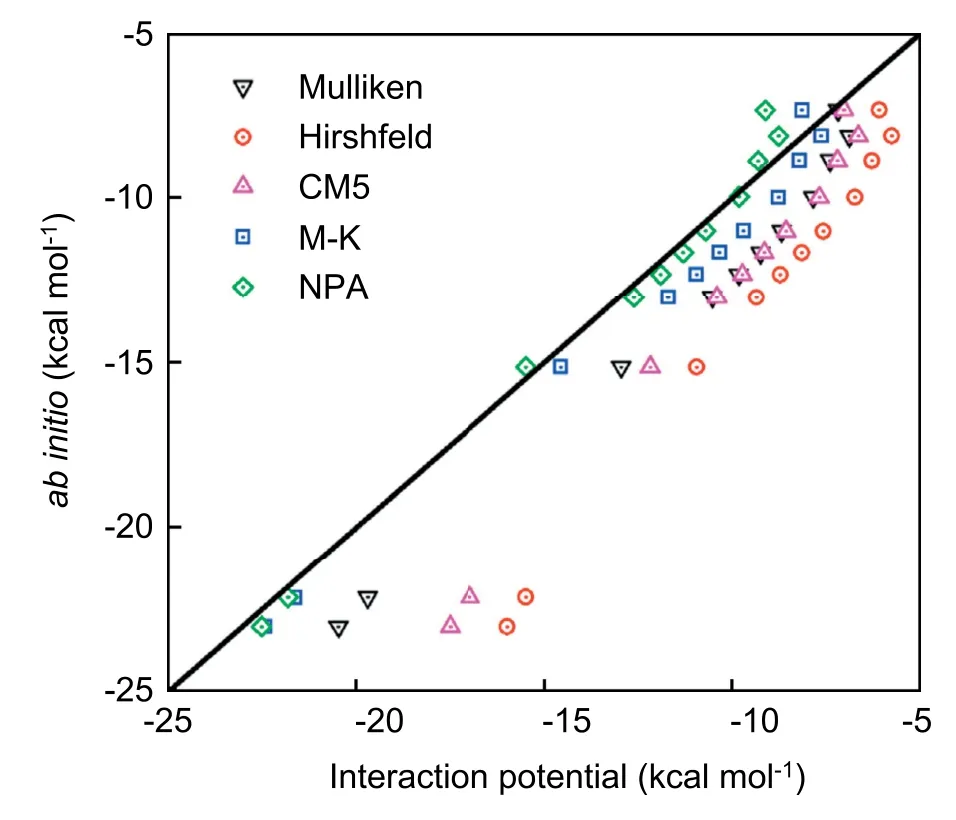
Fig.3.The correlation between quantum DFT calculations and interaction potential results for the solute-solvent interaction.

Afterwards,the free energy profile in aqueous solution is determined by using RxDFT,as shown in Fig.5.The free energy profiles in aqueous solution from RxDFT using MK(ESP) charge model (RxDFT-ESP) and NPA charge model(RxDFT-NPA) agree well with the result from the RISM method.The predictions of the reaction free energies in aqueous solution from RxDFT-ESP and RxDFT-NPA are 5.96 kcal mol-1and 7.95 kcal mol-1,respectively.These results present an excellent agreement with the results of 7.75 kcal mol-1from the RISM method.The position of the products predicted by the RxDFT,i.e.,Rc=1.49 Å,is similar to the value of Rc=1.47 Å from the RISM method.The values of the activation free energy in aqueous solution are 16.23 kcal mol-1and 16.46 kcal mol-1respectively,which are smaller than the value of 21 kcal mol-1from the RISM method but much closer to the experimental data,9 kcal mol-1[43].This discrepancy might come from the less accurate predictions of the solvation free energy for the hydroxyl by using OPLS/AA force field parameters due to the neglect of the size of hydroxyl hydrogen.The solvent effect is addressed by the comparison between the free energy profile in aqueous solution with the gas-phase free energy profile determined at HF/6-31+G(d) level from ref.42.According to the remarkable solvent effect,there is an obvious increase in the reaction barrier in aqueous solution.The shift of the transition state from Rc=2.39 Å in the gas phase to Rc=2.00 Å in aqueous solution is also captured by the RxDFT method.In addition,due to the solvent effect,the reaction becomes endothermic in the aqueous solution,rather than exothermic in the gas phase.

Fig.4.The RDFs of water molecule around the carbon atom in(a)reactant,(b)transition state,and(c)product from classical DFT(solid line)compared with MD simulations (dash-dotted line).

4.2.OH- nucleophilic attack on CO2

Similar to the reaction of OH-+HCHO,the intrinsic reaction energy profile and free energy profile in the aqueous solution are determined by RxDFT.Fig.6 shows the intrinsic reaction energy profile for the reaction of OH-+CO2.The optimized geometry parameters and the charge distributions are collected in Table S2 in the SI.

Five charge models are also tested,and the results are shown in Fig.7.The result of the solute-solvent interaction from the NPA charge model captures the result from quantum DFT calculations.Then,the classical DFT calculations of the solvation free energies are carried out with the charge distributions from the NPA charge model.Meanwhile,the solutesolvent radial distribution functions (RDFs) of reactants,TS,and products are determined.In Fig.8,the RDFs for the aqueous oxygen around carbon,carbonyl oxygen,and hydroxyl oxygen are given.

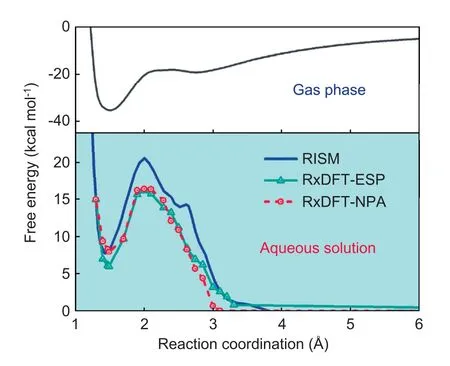
Fig.5.Reaction free energy profiles for the nucleophilic addition reaction of OH-+HCHO in aqueous solution and in the gas phase.Reaction free energy profile in aqueous solution from RISM(blue solid line)[43];RxDFT-ESP(green solid line with triangles);RxDFT-NPA (red dash line with circles) are compared.The gas-phase free energy profile determined at HF/6-31+G(d)level from ref.42,black solid line.

Fig.6.Intrinsic reaction energy profile along the reaction coordinate for the reaction of OH-+CO2.

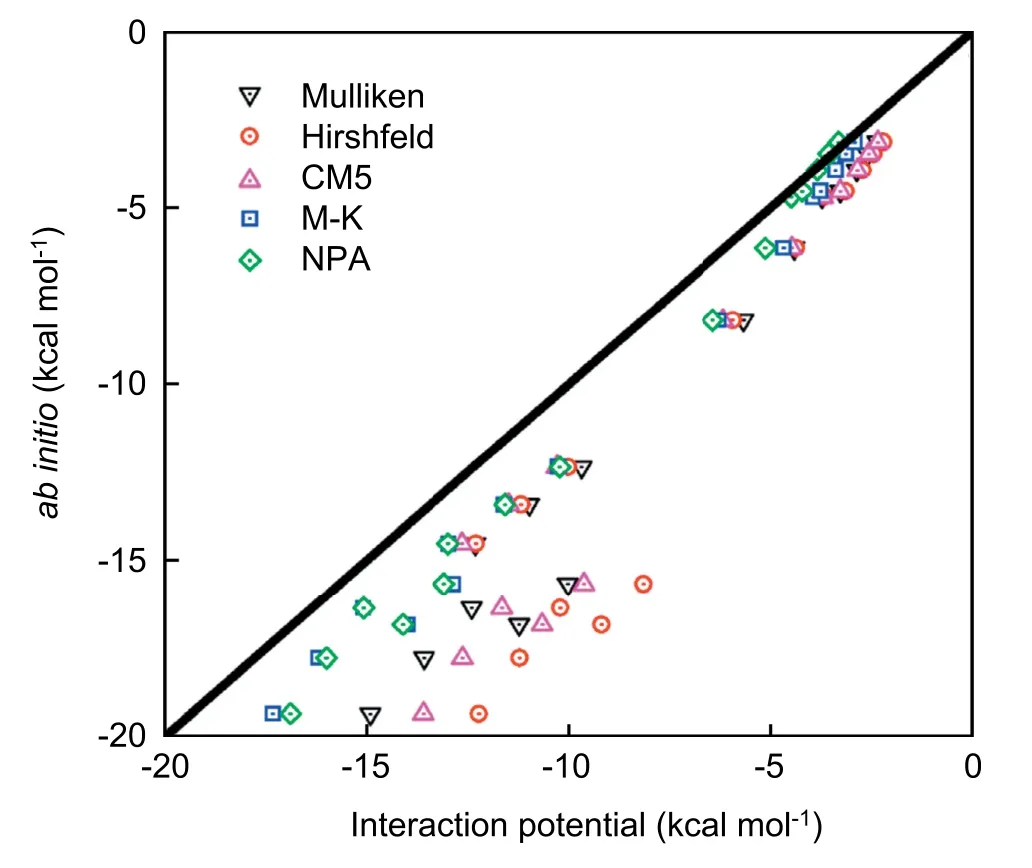
Fig.7.The correlations between quantum DFT calculations and interaction potential results for different types of solute-solvent interactions.

Fig.9 presents the free energy profile for the reaction of OH-+CO2in aqueous solution,and the prediction from the RxDFT method agrees well with the results from molecular dynamics free energy perturbation (MD-FEP) simulations.As shown in Fig.9,the free energy profile has a pure solvationinduced reaction barrier since the gas-phase free energy profile is monotonic.The activation free energy in aqueous solution from RxDFT calculations is 17.78 kcal mol-1with DHS=2.95 Å and 18.82 kcal mol-1with DHS=2.85 Å at Rc=2.0 Å,respectively.The results present an excellent agreement with those from MD-FEP calculation,17 ± 2 kcal mol-1.The reaction free energy in the aqueous solution,-5.48 kcal mol-1with DHS=2.95 Å and-4.86 kcal mol-1with DHS=2.85 Å,much larger than the value of-45.47 kcal mol-1[41]in the gas phase owing to the solvent effect.Meanwhile,there is a shift,about 0.1 Å,on the position of the reaction free energy in aqueous solution,relative to the position in the gas phase.

4.3.OH-+HCHO reaction at solid–liquid interface

In previous work [64,65],it has been found water-filled cavitands could impose significant effect on the molecular confirmation of a confined alkane chain.To explore the substrate effect on chemical reaction,here we extend the RxDFT method to an inhomogeneous system near a graphene wall for studying the complex solvent effect on the reaction of OH-+HCHO.In this study,the wall-water interaction is described by Steele's 10-4-3 potential[66],and the interaction between cluster and wall is not considered as it’s irrelevant with the reaction free energy.During the numerical calculation,the cluster is fixed with the hydroxyl and carbonyl group located on the xoy plane.The cluster-wall distance,d,is defined then as the separation of the xoy plane to the substrate surface.The DHS is chose to be 2.85 Å.Fig.10 plots the solvation free energies of the transition state (TS),product,and reactants (HCHO and OH-) at different cluster-wall distances.When the distance is less than 10 Å,the solvation free energies are depressed as decreasing the distance.This trend stemms from the alteration of local solvent structure subject to the wall-water interaction.When the distance is large than 10 Å,the solvation free energy remains unchanged and recovers to the bulk value in the aqueous solution,indicating the substrate has then little effect on the solvation free energy.For further interpret the substrate effect,the density distributions of water around solute cluster at different distance to the wall are plotted.

Figure 11 shows the density maps of water molecules around the transition state (TS) at different cluster-wall distances.The layer-by-layer water structure is found in the vicinity of the graphene-like wall and around the transition state owing to the wall-water interaction and cluster-wall interaction.As shown in Fig.11 (a) and (b),since the water density turbulence overlaps in the region between the wall and cluster,the first and second density peaks slightly rise at d=6.0 Å and d=8.0 Å,respectively,which reduce the solvation free energy of the cluster when the cluster-wall distance is less than 10 Å.When the cluster-wall distance is sufficiently large,the layerby-layer water structures around the wall and TS don't overlap as shown in Fig.11 (c) and (d),and in this case the solvation free energy of TS approaches to the value in the bulk system.

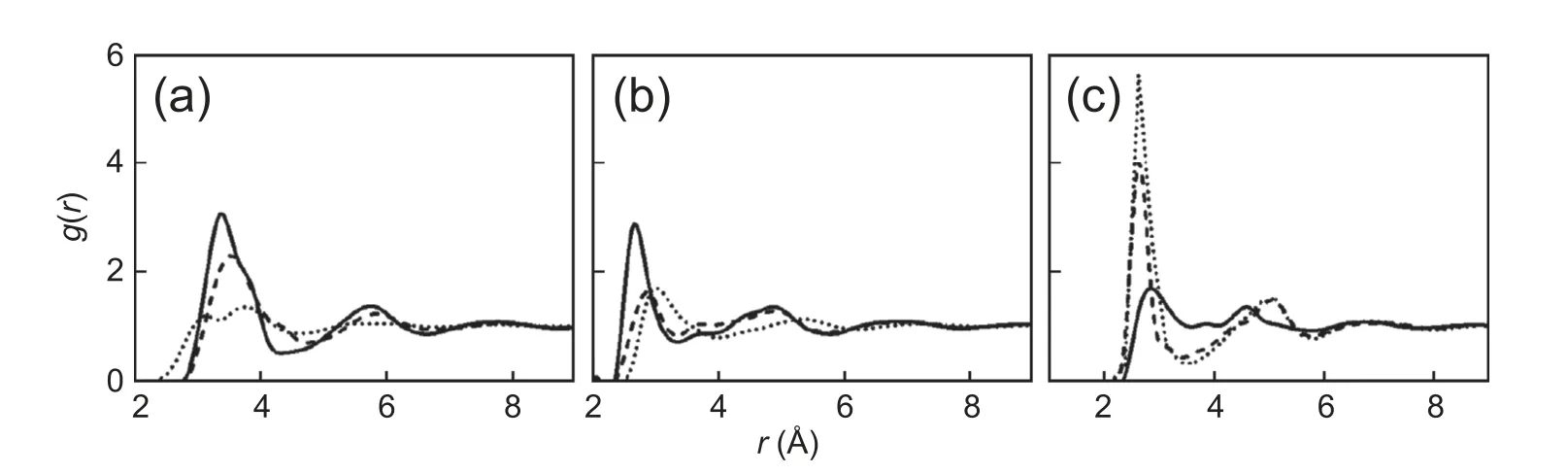
Fig.8.RDFs of aqueous oxygen around(a)carbon,(b)carbonyl oxygen,and(c)hydroxyl oxygen for the product(solid line),transition state(short-dashed line),and reactant (short-dotted line).

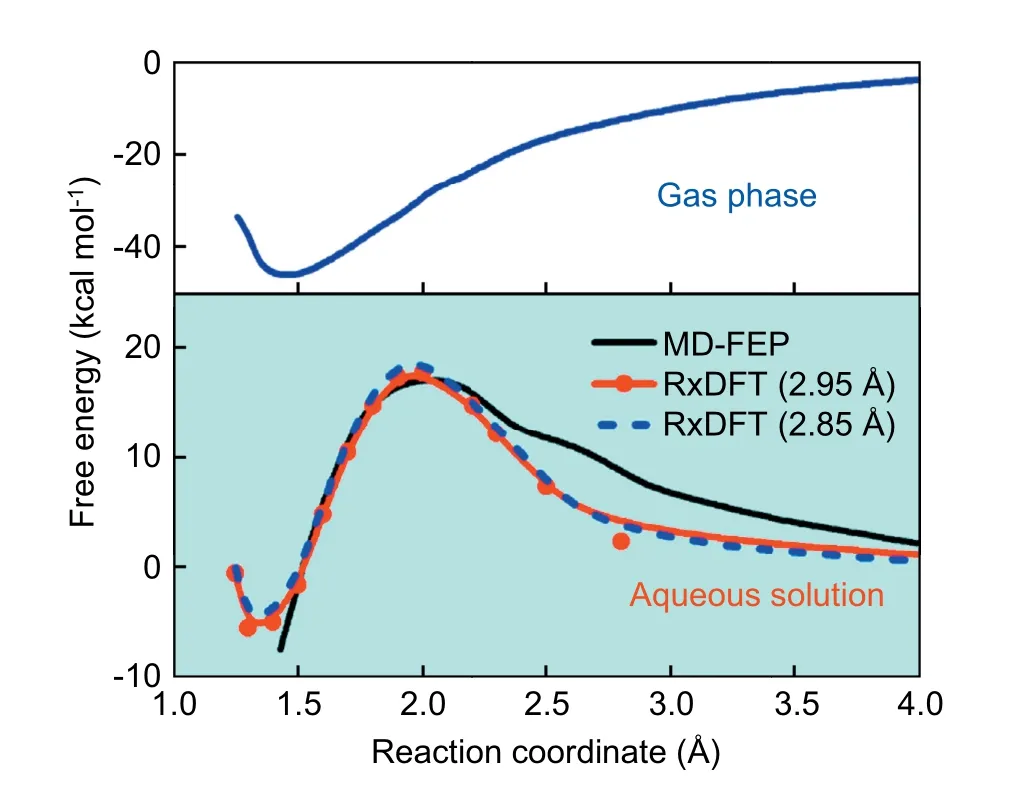
Fig.9.Reaction free energy profile for the nucleophilic addition reaction of OH-+CO2 in aqueous solution or in the gas phase.Reaction free energy profile in aqueous solution from MD-FEP (black solid line);RxDFT with DHS=2.95 Å (red solid line with circles);and RxDFT with DHS=2.85 Å(blue dashed line),respectively.The gas-phase free energy profile determined at LMP2/6-311++G(d,p) level from ref.41,blue solid line.

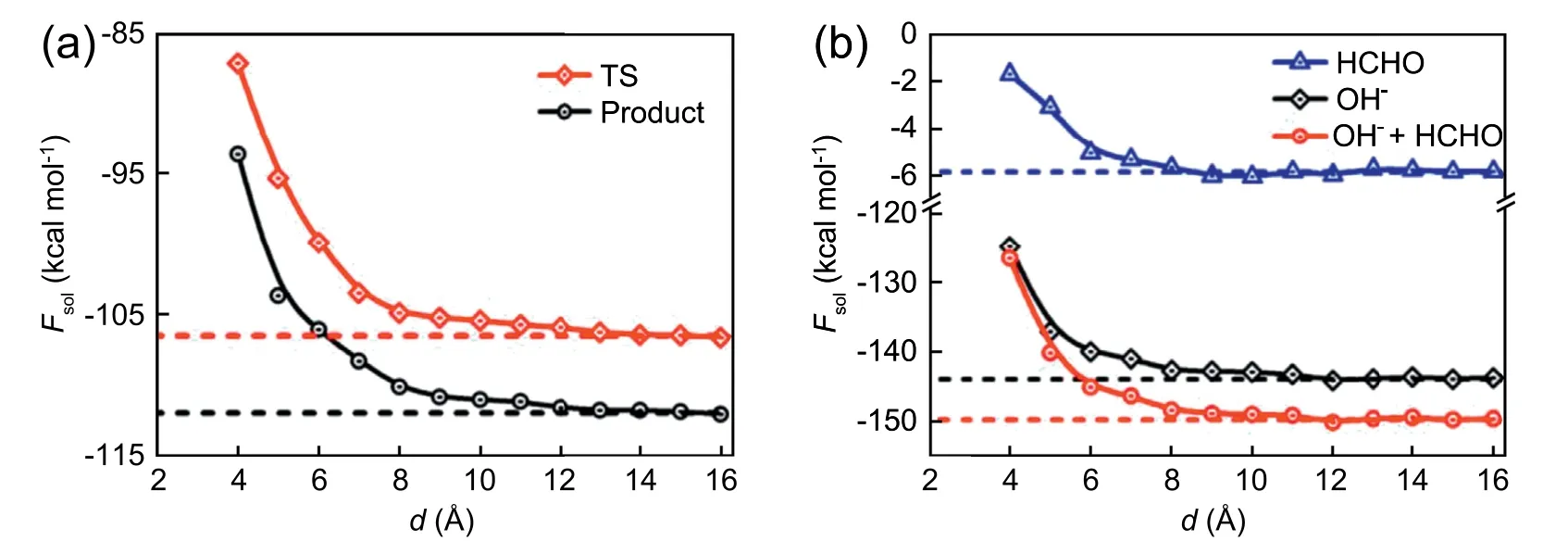
Fig.10.Solvation free energy for (a) TS,product,and (b) reactants (HCHO and OH-) as a function of the distance between clusters from the wall.

Fig.11.Density maps of water around the TS cluster at different cluster-wall distances with (a) d=6.0 Å;(b) d=8.0 Å;(c) d=11.0 Å;(d) d=15.0 Å,respectively.

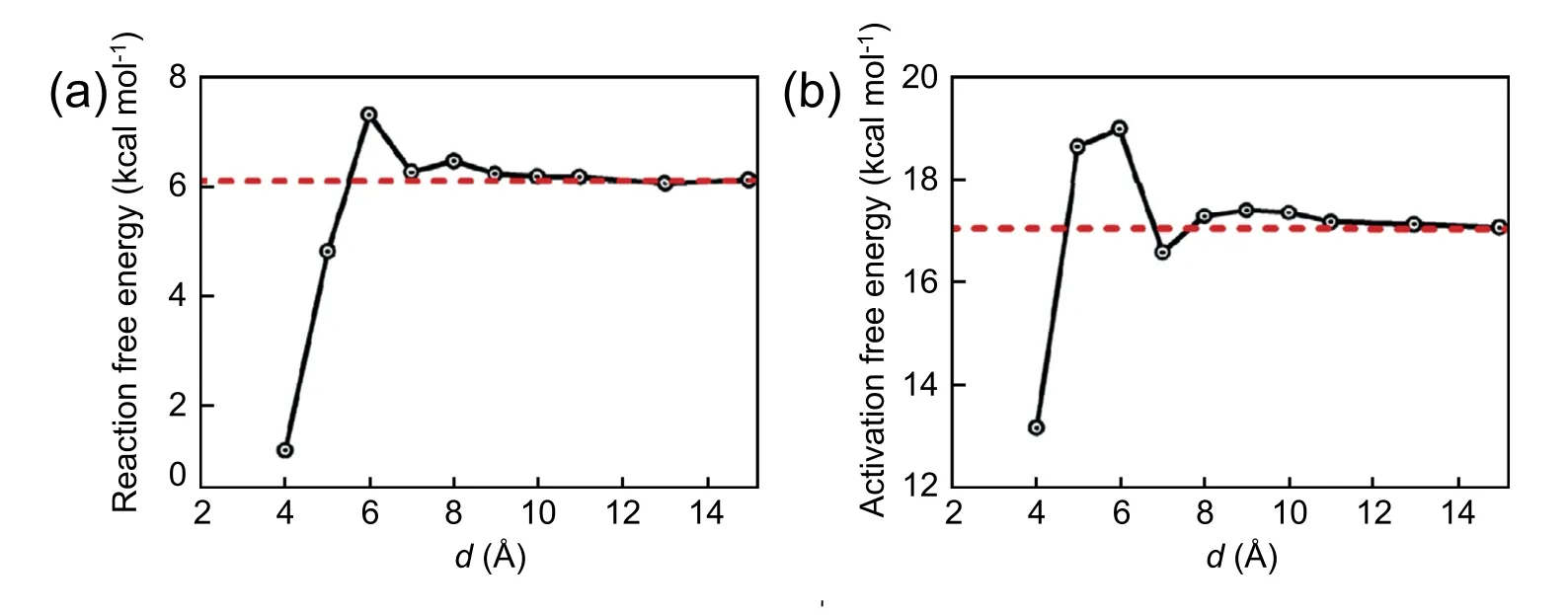
Fig.12.Reaction and activation free energy as a function of the cluster-wall distance.

The reaction free energy and activation free energy profiles varying with the cluster-wall distance are plotted in Fig.12.As discussed above,the reaction free energy and activation free energy recover to their cor111responding bulk values when the cluster is far away from the wall.In other words,when the reaction takes place in the interfacial area with cluster-wall distance exceeding about 10 Å,the presence of substrate has little effect on the reaction profile.However,when the clusterwall distance is less than 10 Å,the substrate effect on the reaction profile becomes profound.Specifically,the reaction free energy and activation free energy first increase and then decrease as decreasing the cluster-wall distance.As shown in Fig.12 (b),the activation free energy is about 4 kcal mol-1less than the barrier energy in bulk system when the reaction core is close to the wall with d=4.0 Å.It means that the noncatalytic substrate displays a catalytic effect and the reaction is more likely to occur at the graphene-water interface owing to the solvent effect combined with substrate effect.This trend generally accords with the relevant studies.For example,a recent theoretical study with the help of quantum DFT calculation shows that the reaction barrier for the Menshukin SN2 reaction between ammonia with methyl chloride is reduced by 1.5,2.2,4.0,6.4 or 5.6 kcal mol-1when the reaction occurs at the distance of 5.00,3.75,3.25,3.00,or 2.50 Å from a non-catalytic C42H18graphene sheet [67].In experiment,it is found that there is a significant enhancement of reaction rate when the nucleophilic attacking reaction of MeIm and MeSCN into [Mmim]+[SCN]-occurs in the nanoscale silica pores of MCM41.Particularly,it has been found that activation energy decreases by 5.6 kJ mol-1relative to the bulk reaction when the pore size is reduced to 2.8 nm [68].

5.Conclusions

We successfully extend the reaction density functional theory (RxDFT) to investigate the solvent effect and free energy profiles for two nucleophilic addition reactions in bulk aqueous solution,and we extend the RxDFT method to firstly study the complex solvent effect of OH-+HCHO reaction at solid-liquid interfaces.

For the nucleophilic reaction of OH-+HCHO,the remarkable solvent effect leads to an obvious increase in the activation free energy and reaction free energy,and a shift in the position of the reaction barrier.The free energy profiles in bulk aqueous solution,including the activation free energy and reaction free energy,predicted by using RxDFT are quantitatively consistent with the prediction from the RISM method.For the reaction of OH-+CO2,the solvent effect is profound since it causes a reaction barrier in the aqueous solution,relative to its monotonic gas-phase free energy.The predictions of the activation free energy and the free energy profile in bulk aqueous solution based on RxDFT present a satisfactory agreement with the results from MD-FEP simulations.

Extending the reaction of OH-+HCHO to solid-fluid interface,the reaction free energy and activation free energy profiles varying with the distance to the graphene-like substrate are observed through the RxDFT calculation.When the reaction occurs at a close distance to the substrate surface,the activation free energy is much lower than that in bulk aqueous solution.The activation free energy gradually recovers to the cor111responding value in the bulk aqueous solution when the distance increases.When the distance is beyond 10 Å,the substrate has little effect on the activation free energy.

In addition to our previous studies in which the RxDFT method was used to successfully expatiate the solvent effects of two nucleophilic addition reactions in aqueous solution,the inhomogeneous solvent effects on the OH-+HCHO reaction at solid-liquid interfaces are further explored by using the RxDFT method.Thus,this work casts helpful insights into the solvent effects on the two nucleophilic addition reactions both in bulk aqueous solution and at solid-liquid interfaces.

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Acknowledgments

This work is supported by National Natural Science Foundation of China (Nos.91934302,21878078 and 21808056).

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.gee.2020.11.028.