类Starship 飞行器大迎角动态特性数值研究

吕凡熹，赵 飞，刘 瑜，杜若凡，石 泳，张宇佳

（中国空间技术研究院钱学森空间技术实验室，北京 100094）

人类载人航天事业经历了60 多年的发展历程，形成了载人飞船和航天飞机为代表的两类天地往返载人航天运输器，此外便少有跨越性的突破。近年来，民营商用航天公司为该领域注入了新的活力，其中以SpaceX 公司研发的Starship 最为突出。有别于传统伞降和机场水平降落的回收方式，Starship 利用操纵面的气动力和火箭发动机矢量推力联合控制完成再入减速和着陆过程，从而实现了可重复使用，显著降低发射成本［1-2］。需要指出的是，再入过程的稳定飞行涉及很多关键技术，其中动态稳定性的水平将决定飞行任务的成败［3］。由于Starship 仅在着陆末端利用矢量推力进行飞行控制，要保证飞行器姿态受控，并且为乘员提供良好的生存环境，Starship 新颖气动外形的动态稳定性是否良好至关重要。

为满足快速再入减速需求，Starship 全程采用大迎角飞行，这必然带来复杂的非定常流动问题。而非定常分离、旋涡和非定常运动激波及其与附面层的干扰使其流场呈现强烈的非线性效应，致使动导数辨识也十分困难［4］。同时，Starship 再入过程中要经历宽速域、大空域的飞行条件，若通过风洞试验或者在飞行试验阶段对其动态稳定性进行研究，将导致飞行器设计周期成倍增加，设计成本大幅增长。随着近年来计算流体力学（Computational fluid dynamics，CFD）及大规模高性能计算技术的迅猛发展，国内外飞行器动态特性的研究广泛应用了非定常CFD 方法。文献［4-7］采用强迫振动法，数值模拟了弹道外形、尖锥、钝锥、导弹以及返回舱等典型飞行器的动导数，结果表明飞行器在小迎角下动导数具备一定的线性特性。文献［8］研究了弹道外形以及有翼导弹的大迎角下的动态特性，结果表明飞行器在大迎角下动导数具备非线性特性。上述主要还是针对简单外形、单一速域下的研究工作，而复杂外形飞行器大迎角、宽速域非线性动态特性研究则相对较少。因此，应该充分利用非定常CFD 方法对Starship 这类创新构型飞行器的动态特性进行详细分析，从而充分降低设计成本，尽可能减少设计风险。

非定常CFD 方法求解动导数充分评估流场的非线性特性，且能辨识更全面的动导数，主要方法有：强迫振动法［9］、自由振动法［10］、准定常法［11］和谐波平衡法［12］。强迫振动法可辨识的动导数种类较其他方法更为全面，对交叉导数、交叉耦合导数、加速度导数均能较好地开展计算评估；自由振动法的模拟过程与真实飞行情况状态吻合度更高，但对辨识方法要求高，计算工作量大，仅适用于平衡状态下的动导数计算，且动导数计算种类有限；准定常法计算精度高且速度快，但只能用于旋转导数的评估；谐波平衡法计算效率高，但是对非定常流动的计算精度远低于上述时域计算方法。

因此，本文采用基于小振幅强迫振动法的非定常CFD 方法对类Starship 飞行器宽速域、大空域、大迎角再入减速过程的动态特性进行系统评估。本文采用一种基于分区弹簧近似法动网格技术的三维非定常N-S 方程有限体积法进行了飞行器动态特性的仿真评估，经HBS 标准模型验证，计算精度满足需求。应用该方法深入评估了类Starship飞行器再入过程中的动态特性，包含不同马赫数、重心位置、操纵面偏转、迎角以及减缩频率对飞行器俯仰组合导数的影响。

1 计算方法

1.1 控制方程

本文采用有限体积法求解非定常可压缩N-S方程，其三维积分形式为

本文有限体积法在空间方上采用Piecewise Linear 方法进行变量重构，对流通量的计算选择二阶精度Roe 格式以及Venkatakrishnan 限制器，湍流模型选取SST 两方程模型。时间方向上采用基于GMRES 算法的全隐式迭代求解。

1.2 动网格方法

强迫振动方法需要使用动网格技术，而大量相关研究中强迫振动方法的数值模拟常采用刚性网格法［13］、滑移网格法［14］以及重叠网格法［15］，这3 种方法能有效保持网格品质，但刚性网格法在远场边界、滑移网格法在滑移面和重叠网格法在重叠区，均会因插值误差而导致计算误差，并将随时间累积不断放大。而强迫振动法振动幅度较小，弹簧近似法既能满足动网格的需求又可避免插值误差的产生。文献［16］中提出了线性弹簧近似法并将其应用于机翼颤振问题，但是线性弹簧模型易导致负体积现象的出现。为此，文献［17］中增加了扭转弹簧模型进行完善。此后弹簧近似法不断改进并开展了大量的应用。

但是，传统的弹簧近似法无论改进与否，对复杂问题的处理效率和稳定性仍然有限［18］。因此，本文采用一种基于分区思想的弹簧近似法动网格技术，相比传统的弹簧近似法，该方法计算量小且可保持较高网格质量，进而在避免插值误差的基础上保证数值计算的稳定性。如图1 所示，计算网格被分成刚性网格区和弹性网格区。刚性网格区是包含整个飞行器及其周边边界层网格的球形区域，区域几何中心为飞行器质心，也是强迫振动中网格的转动中心。该区域要求足够大确保该刚性网格区外边界附近的网格质量较高。刚性网格区之外其他计算区域均为弹性网格区。在强迫振动过程中，刚性网格区与飞行器固连，其网格整体随飞行器做强迫振动，从而保证壁面附近的网格质量不因边界运动而变差。弹性网格区则以刚性网格区外边界作为运动边界，该区域网格中每条边为弹簧模型，各个网格点在周围网格点的作用力下达到受力平衡，每个网格点的静态平衡方程为

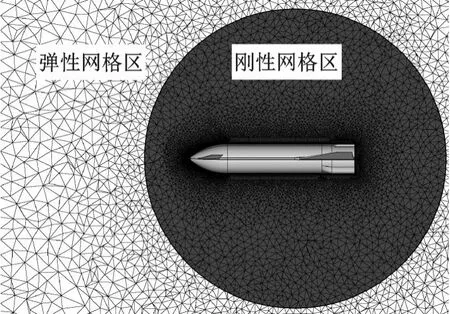
图1 基于分区弹簧近似法的计算网格Fig.1 Computational grid based on partitioned spring analogy method

图2 给出了采用分区弹簧近似法从平衡位置振动到最大振幅过程中的网格变形过程，为方便展示，图2（b）最大振幅达到了45°。由图2 可见，在网格变形过程中刚性网格区网格没有形变，有效保证了区内网格质量。弹性网格区由于本身网格质量较好，虽然在变形过程中会有所下降，但能保证非定常动态计算的鲁棒性。以图2 中展示的NACA0012 翼型的强迫振动为例，振幅达45°时不同工况的计算仍能保持时间迭代正常推进，双时间步内迭代能有效收敛，流场结构合理可信。但振幅达60°时，由于刚性区大幅度地扭转，弹性区网格质量已不能确保非定常计算的正常进行。但是，对于动导数计算所采用的小振幅强迫运动法，求解过程中振幅较小，弹性网格区的网格变形后质量不会出现显著下降，更不会出现负体积等极端情况，本文方法能充分满足强迫振动法的网格变形需求。

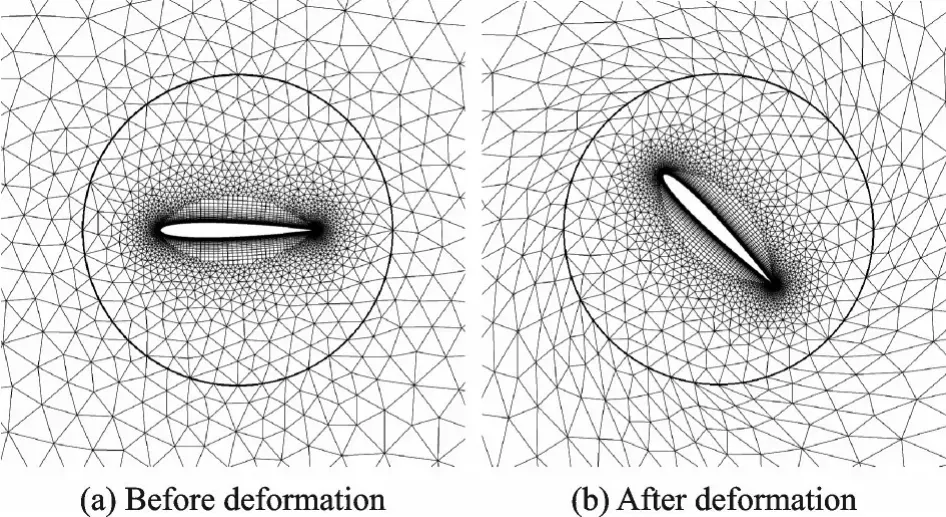
图2 网格变形过程Fig.2 Mesh deformation process

1.3 动导数辨识

本文采用小振幅强迫振动法辨识飞行器动导数。以俯仰动导数为例，在体轴坐标系下，给定绕质心的强迫运动形式（无量纲形式）为

2 算例验证

为了验证数值方法的准确性，选取高超声速弹道外形（Hyper ballistic shape，HBS）来作为验证算例。HBS 由1 个半球柱和2 段扩张尾裙组成，该外形有较为精确的试验结果［19］，常被用作验证标模。

验证算例的流动条件为：Ma=6.85，基于底部直径的Red=0.72×106，纵向质心位置Xcg/L=0.72。数值计算时取流动条件为：压力461.51 Pa，密度0.005 545 kg/m3，温度290 K，计算时参考长度取头部直径d=1 m，参考面积为0.785 498 m2，几何外形如图3 所示。迎角分别取α0=0°、3.068 9°、6.443 7°、9.054 5°、13.388 1°、15°、20°，振幅取αm=1°，减缩频率k=0.01。

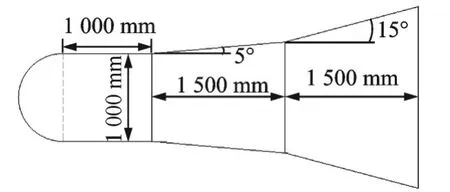
图3 HBS 几何外形Fig.3 HBS geometry

图4 给出了本文计算结果和试验数据以及文献［15］中的CFD 计算结果的对比。结果可见，所有计算工况动导数均为负值。当迎角小于13°俯仰动导数变化相对较小，当迎角大于13°俯仰动导数迅速减小，俯仰动稳定性增加。本文结果与试验数据吻合度较好，误差小于9%，同时对于缺少试验数据的20°迎角工况，本文结果与文献CFD 结果也误差也较小，证明本文方法对于求解飞行器动导数的有效性。

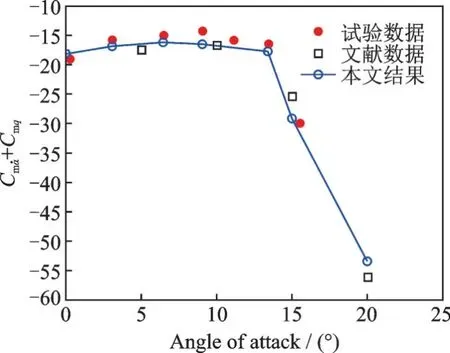
图4 HBS 动导数计算结果对比Fig.4 Comparison of HBS dynamic derivative calculation results

3 类Starship 动态特性分析

3.1 几何外形

本文研究的类Starship飞行器根据SpaceX 官网公布的Starship尺寸信息进行三维建模［20］，飞行器总长50 m，直径d=9 m，如图5 所示。前翼展长15 m，后翼展长18 m，前后翼舵偏范围均为向上偏转0°～60°。考虑大迎角再入过程中，前后翼在避免承受过大的力、热载荷的同时，均需保留足够舵效。因此，除下文分析前后翼偏转对动态特性影响的工况，其他计算工况中使用的模型前后翼均向上偏转30°。

图5 类Starship 飞行器三维模型Fig.5 Starship-like spacecraft 3-D model

3.2 计算网格

本文计算网格采用非结构混合网格，总网格量1 200 万个，物面网格和边界层网格如图6 所示。如无特别说明，下文计算工况质心位于纵向质心位置Xcg/L=0.6，强迫振动的减缩频率k=ωd/2u∞取0.05，振幅取αm=1°。飞行器采用高空高速大迎角的再入方式，故迎角α0取70°，侧滑角β取0°。

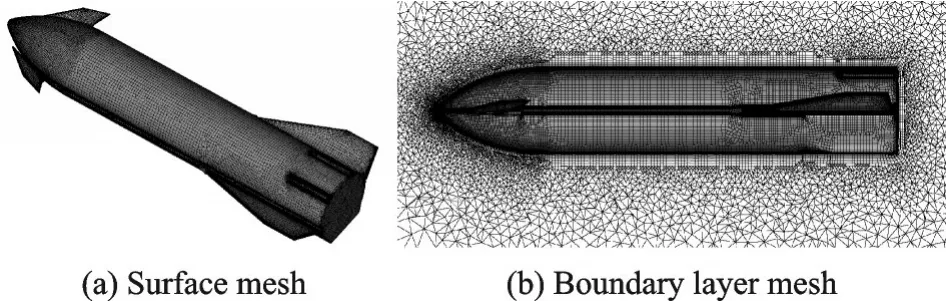
图6 表面网格及边界层网格Fig.6 Surface and boundary layer meshes

3.3 马赫数

类Starship 飞行器再入过程是一个高度和马赫数逐渐减小的过程，参考有翼再入飞行器典型再入弹道，选取不同高度下，70°迎角、0°侧滑、前后翼操纵面偏角均为30°，Ma范围为0.3～10 的计算工况，如表1 所示。

表1 计算工况Table 1 Computation cases

图7 给出了Ma=0.3、0.9、1.5、5.0 时，1 个周期初始时刻的计算流场，图中展示了飞行器表面和流场对称面的压力分布及马赫数等值线的分布情况，迎风面整体高压、背风面低压，背风面尾部存在大分离区，从高速结果中可以清晰识别流场中的波系，仿真结果的流动结构合理可信。图8（a）给出了Ma=5.0 工况俯仰力矩系数的迟滞环曲线。迟滞环形状饱满展示了非定常运动时物体表面气动力的作用和物体运动之间存在较强的时间延迟和滞后效应，并在计算开始后1 个周期内即进入迟滞环。从时间历程上看非定常气动力矩系数随时间步的增长很快按周期规律达到谐振状态，如图8（b）所示。

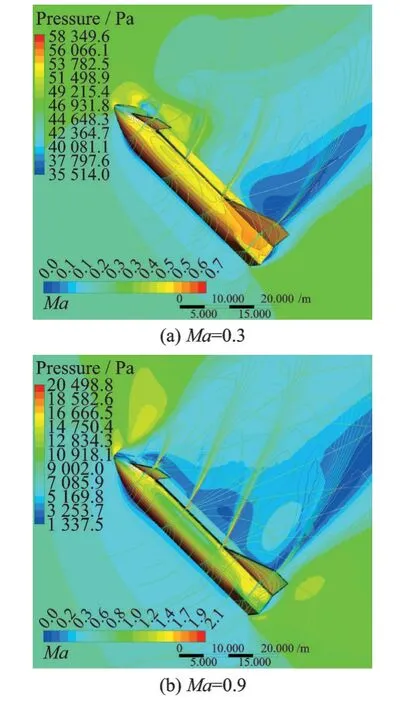
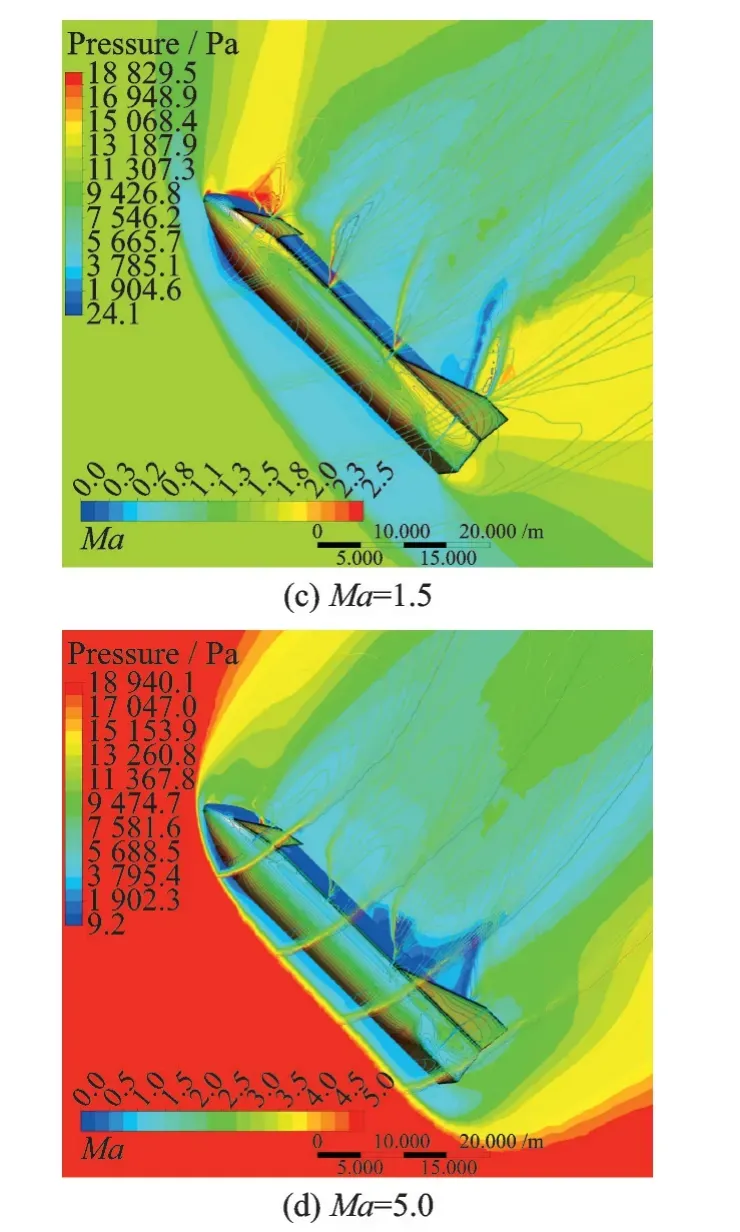
图7 1 个周期初始时刻表面压力和流场马赫数云图Fig.7 Surface pressure and flow field Mach number contour at initial moment in one period

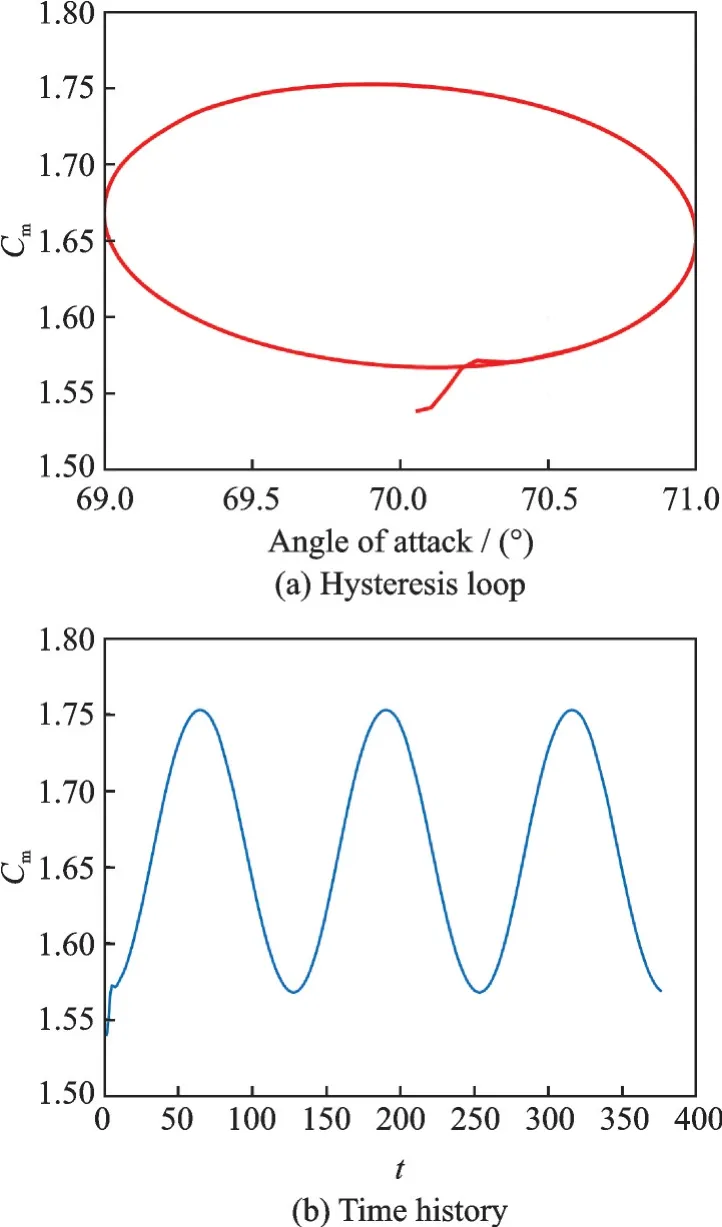
图8 俯仰力矩系数的迟滞环和时间历程(Ma=5.0)Fig.8 Hysteresis loop and time history of pitching moment coefficient(Ma=5.0)

图9 给出了计算得到的飞行器俯仰组合导数随飞行马赫数的变化，可见再入过程中飞行器从高超声速逐渐减速至Ma=2.0 时，其俯仰组合导数均为负值且变化较小，非定常气动力对飞行器俯仰振动运动起阻尼作用。当Ma＜2.0 飞行器减速进入跨声速区，俯仰组合导数开始增大，在Ma=0.8 附近由负值变为正值，Ma=0.6 附近达到峰值。飞行器进一步减速进入亚声速区域，俯仰组合导数由峰值开始减小但仍为正值。

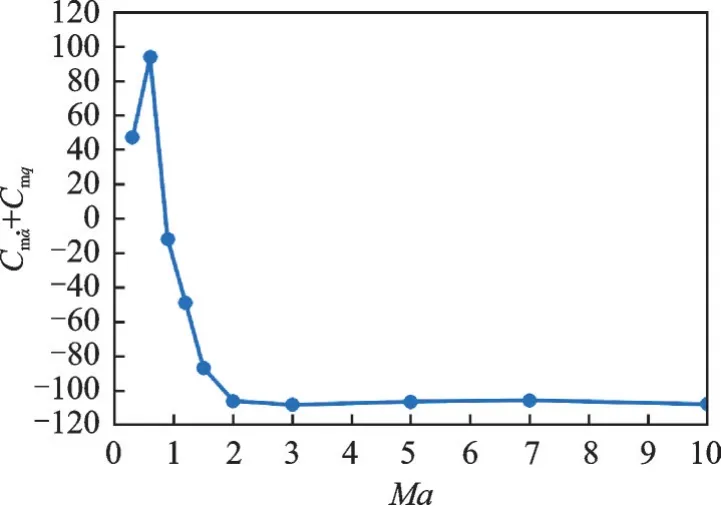
图9 大迎角俯仰动导数随不同马赫数的变化Fig.9 Variation of pitch dynamic derivative with different Mach number at high angle of attack

3.4 重心位置

在飞行器飞行过程中，随着推进剂的消耗，重心会随之变化。为了研究重心位置对飞行器俯仰动导数的影响，选取来流马赫数Ma=0.3 和5.0，迎角α0=70°，纵 向 质 心 相 对 位 置Xcg/L=0.3、0.45、0.6、0.75 进行俯仰组合导数辨识，如图10所示。

图10 不同质心位置Fig.10 Different centroid positions

图11 给出了Ma=0.3 工况不同质心位置时俯仰力矩系数的迟滞环曲线和时间历程，力矩系数经过了大约1 个周期后才呈现稳定的周期振荡。同时强迫振动过程中初始迎角位置处的力矩系数大幅度偏离定常解，表明低速流动下气动力的非定常效应对气动特性影响极为显著。

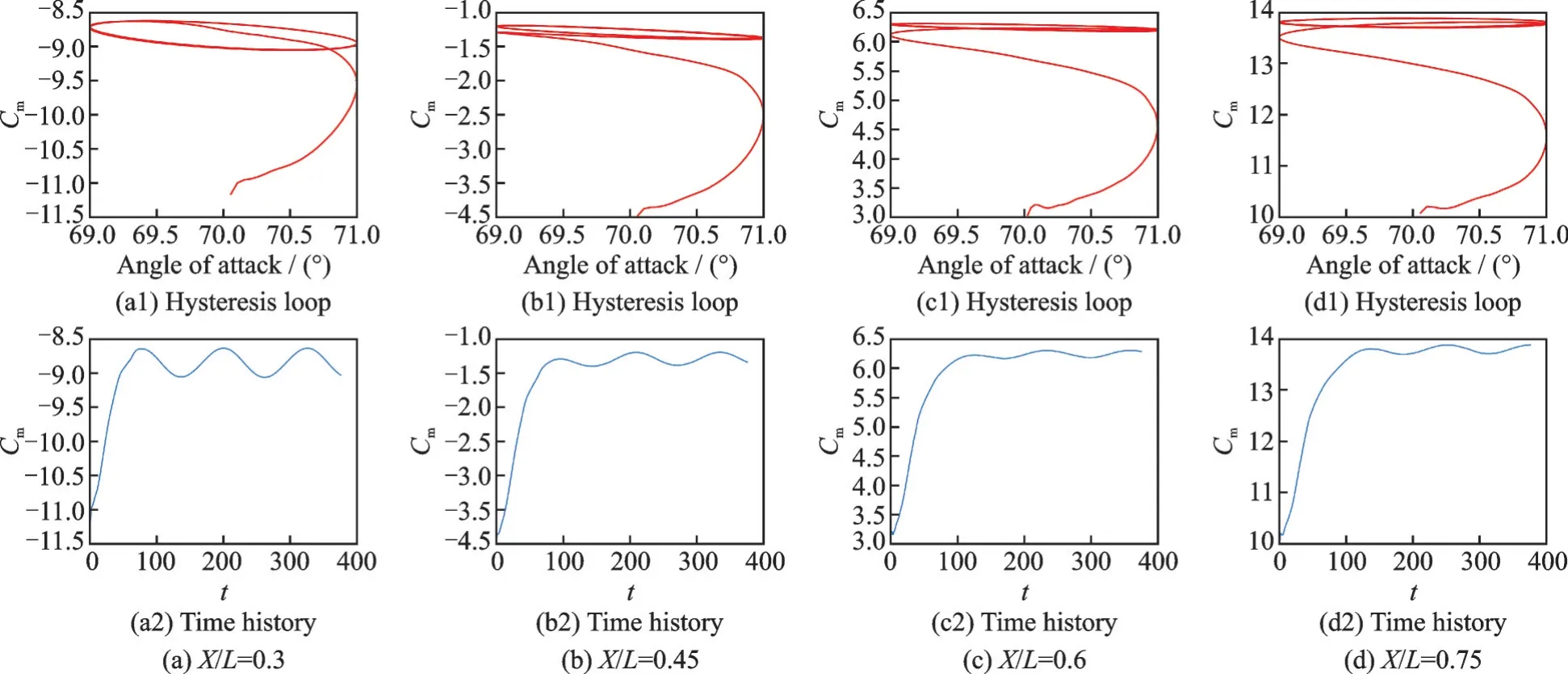
图11 不同质心位置俯仰力矩系数的迟滞环和时间历程（Ma=0.3）Fig.11 Hysteresis loop and time history of pitching moment coefficient at different centroid positions（Ma=0.3）

图12 给出了Ma=5.0 工况不同质心位置时俯仰力矩系数的结果，其力矩系数经历不到半个周期即发展成稳定的周期振荡，初始迎角位置处的力矩系数偏离定常解的幅度相比Ma=0.3 工况结果要小很多，高速流动下非定常效应的影响要小于低速流动。

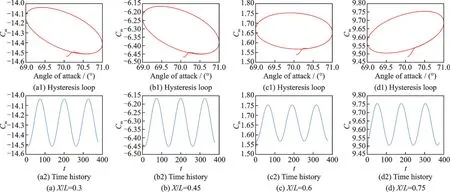
图12 不同质心位置俯仰力矩系数的迟滞环和时间历程（Ma=5.0）Fig.12 Hysteresis loop and time history of pitching moment coefficient at different centroid positions（Ma=5.0）

图13 给出了不同质心位置对俯仰组合导数的计算结果。对于Ma=0.3，随着质心位置后移，俯仰动导数逐渐增大，当质心位于Xcg/L=0.53 之后，俯仰动导数变为正值，呈动态不稳定状态。对于Ma=5.0，随着质心位置后移，俯仰动导数先增大后减小，最大值出现在质心位于Xcg/L=0.6 左右，俯仰动导数均为负值，呈动态稳定状态。

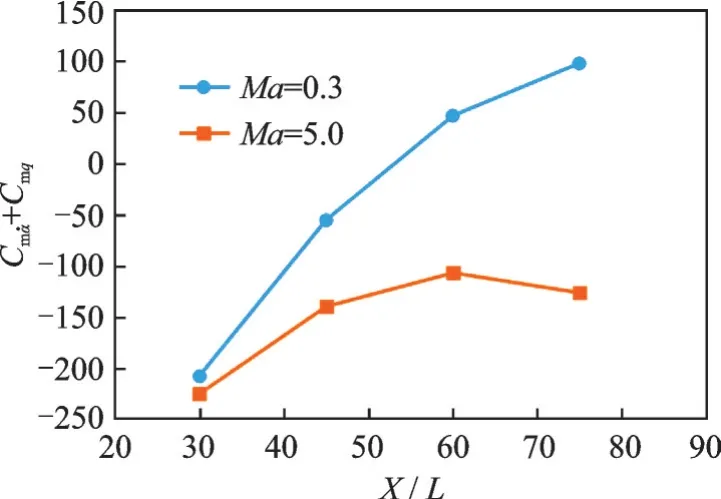
图13 大迎角下质心位置对俯仰动导数的影响Fig.13 Effect of centroid positions on pitch dynamic derivative at high angle of attack

3.5 操纵面偏转角

为评估飞行器高速再入过程中前后翼操纵面偏转对俯仰动导数的影响，选取马赫数Ma=5，迎角α0=70°，选取前翼、后翼、前后翼同步3 种模式，按0°、30°、60°的舵偏状态进行评估，动导数计算结果如图14 所示。可见，随着前/后翼偏转角逐渐增大，俯仰动导数呈单调上升的趋势，前/后翼舵偏均将导致飞行器俯仰动稳定性减弱。对比前/后翼偏转的两种模式，前翼偏转对俯仰动导数的影响相对较小，而后翼偏转则影响更为显著。同时，前后翼同步偏转对俯仰动导数的影响与后翼偏转相当，并没有呈现出前后翼偏转作用累加的现象。主要原因是前翼投影面积明显小于后翼，因此前翼对动导数的影响较后翼会小很多。同时大迎角高超声速流场非线性程度大，激波和分离同时存在，动导数不会随前后翼大幅度偏转呈现简单的线性变化特征。

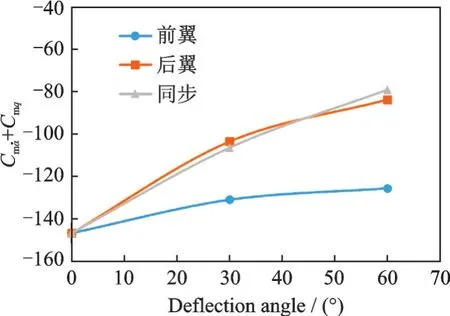
图14 大迎角下俯仰动导数随操纵面偏转的变化Fig.14 Variations of pitch dynamic derivative with deflection angle of control surface at high angle of attack

3.6 迎 角

为了研究不同迎角对该类飞行器俯仰动导数的影响，根据不同速度下再入过程可能的迎角范围，评估了Ma=0.3、迎角α0=0°～180°和Ma=5.0、迎角α0=0°～90°下的俯仰动导数，其中计算工况的纵向质心位置位于Xcg/L=0.6。图15（a）为Ma=0.3 时，不同迎角俯仰动导数的计算结果。当迎角α0=0°时，俯仰动导数为负值，后随迎角增大，俯仰动导数先后在65°、125°、170°迎角附近经历了3 次变号，动导数为负值的迎角范围 分 布 在0°～65°和125°～170°之 间。图15（b）为Ma=5.0 时，俯仰动导数随迎角的变化曲线。当迎角α0=0°时，俯仰动导数为负值，后随迎角增大，俯仰动导数逐渐减小，在70°迎角附近达到最小值。对于Ma=5.0 所评估的不同迎角的工况，俯仰动导数均为负值，气动力对飞行器俯仰动起阻尼效果。

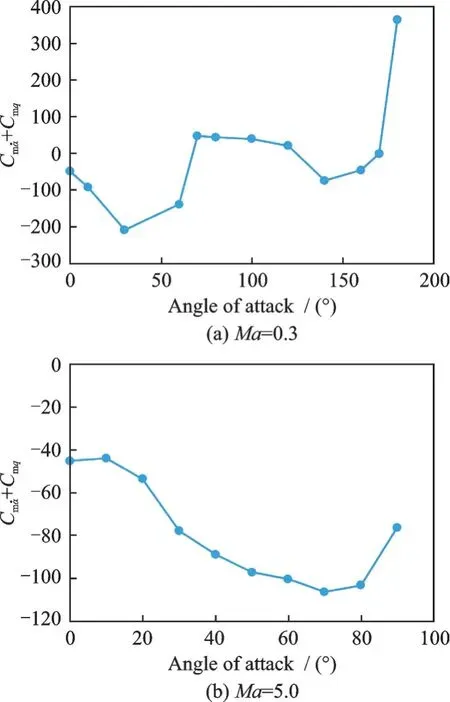
图15 迎角对俯仰动导数的影响Fig.15 Effect of angle of attack on pitch dynamic derivative

3.7 减缩频率

本节评估了不同减缩频率K对大迎角再入过程中俯仰动导数的影响。针对Ma=0.3、5.0，迎角70°，纵向质心位置X/L=0.6，减缩频率分别选择0.01、0.05、0.25、0.50、1.00 开展动导数计算。如图16 所示，对Ma=0.3 的计算工况，动导数在高频不敏感，但在低频时，动导数随减缩频率的降低迅速增大，飞行器从负值转变为正值。对Ma=5.0 的计算工况，动导数对减缩频率的变化不敏感，结果符合对高速飞行器动态特性的经验认识。需要指出的是，减缩频率是影响动导数计算结果的重要因素，适当的减缩频率才能得到正确的计算结果，而减缩频率应由典型飞行状态的气动特性和质量特性估算给出。本文目标是研究类Starship 外形飞行器的动态特性，而通常飞行器超声速下的动态特性动导数随频率变化不大，图16 中，Ma=5.0时的仿真结果也验证了该经验认识。因此在质量特性未知的前提下，上文在减缩频率的常用取值范围内采用0.05 开展了动导数评估，这也是大量研究任务和文献资料中所采取的相对适中的减缩频率。

图16 减缩频率对动导数预测结果的影响Fig.16 Effect of reduced frequency on dynamic derivative prediction result

图17 为不同减缩频率下俯仰运动对应力矩系数的迟滞环曲线的计算结果。当强迫振动过程中力矩系数达到谐振解时，振动频率越高，其迟滞环越饱满，其力矩系数的峰值也越大。同时在相同迎角下，由于运动方向的不同，对应有2 个不同的力矩系数。减缩频率的越小，迟滞环越逼近定常解。而减缩频率的越大，2 个力矩系数的差值也增大，呈现了流场迟滞效应对气动力的影响。对比Ma=0.3 和Ma=5.0 的迟滞环结果，Ma=0.3 迟滞环的长轴会随减缩频率的增大而偏转。减缩频率的物理含义可以理解为在自由来流运动参考长度的时间内物体做简谐振动位置的相位角变化率，因此相同减缩频率下低速结果迟滞环长轴的更强偏转也体现了低速扰动波传播速度更慢，偏离稳态解更显著的流动特征。

图17 减缩频率对迟滞环的影响Fig.17 Effect of reduced frequency on hysteresis loop

4 结 论

本文采用基于分区弹簧近似法动网格技术的强迫振动方法计算研究了类Starship 飞行器在典型大迎角再入飞行状态下（相对质心位置0.6，前后翼向上偏转30°，迎角70°，减缩频率0.05）不同飞行马赫数、重心位置、操纵面偏转角、迎角、减缩频率的俯仰动态特性变化规律，结果表明：

（1）采用典型再入飞行状态时，飞行器超声速的俯仰动导数均为负值，而Ma＜0.9 时的结果则转变为正值。

（2）在相对质心位置0.3～0.75 的变化范围内，随着质心后移，Ma=0.3 时俯仰动导数由负值变为正值，而Ma=5.0 时俯仰动导数则均为负值。

（3）对于Ma=5.0 工况，随操纵面上偏，俯仰动导数逐渐增大，阻尼效应随之减小，且后翼偏转的影响相比于前翼更显著。

（4）Ma=5.0、迎角0°～90°范围内俯仰动导数均为负值，Ma=0.3 时俯仰动导数为负值的迎角范围分布在0°～65°和125°～170°之间。

（5）Ma=0.3 时俯仰动导数的大小与减缩频率密切相关，Ma=5.0 时俯仰动导数则对减缩频率不敏感。

本文研究系统掌握了类Starship 飞行器典型大迎角再入飞行状态下的俯仰动态特性，动导数计算方法适合应用于各类宽速域大空域复杂外形飞行器的动态特性数值仿真。