高速铁路桥梁箱梁温度场有限元分析
汪 禹
(中铁第四勘察设计院集团有限公司 武汉 430063)
桥梁在我国高速铁路中所占比例较大,混凝土箱梁受季节交替、日照作用等因素引起的温度应力与变形,是桥梁耐久性研究中的重要课题。
国内外学者对混凝土箱梁温度场进行了较为广泛的研究,如美国Zuk等[1]分析了太阳辐射、大气温度、风速等气候因素对桥梁结构温度分布的影响。进入20世纪90年代后,随着有限元软件的发展成熟,桥梁结构温度场问题也得到了更全面的研究。刘兴法等[2-8]通过现场实测数据,结合有限元数值模拟,归纳总结了桥梁温度分布特征。目前我国TB 10002-2017《铁路桥涵设计规范》采用沿梁高、梁宽指数分布的温度梯度模式,该模式是否适合我国高速铁路桥梁实际情况,还需进一步的探讨;同时铺设轨道结构及附属设施对高速铁路箱梁的温度场影响较大,不同阶段的箱梁温度分布也有较大区别,故有必要对高速铁路箱梁的温度场做进一步的研究与探讨。
本文以合福高速铁路某32 m简支箱梁为工程背景,利用有限元仿真技术,对高速铁路箱梁日照温度场进行数值模拟,研究箱梁-轨道系统的温度分布特征,探讨高速铁路箱梁及CRTSⅠ型单元双块式轨道的温度梯度模式。
1 箱梁温度场基本理论
桥梁结构发生的热交换主要为太阳辐射、辐射换热及对流换热,具体热交换示意见图1。对于太阳辐射强度,任意表面太阳附属能qs的计算方法见式(1)。
qs=at(Iθ+Iβ+If)
(1)
式中:at为结构表面的太阳辐射吸收率;Iθ、Iβ、If依次代表太阳直接辐射强度、大气散射辐射强度和地表反射辐射强度。

图1 桥梁结构与外界环境的热交换示意图
考虑到对流换热速率与结构表面温度有关,采用Jurges-Nusselt公式[9]计算。
qc=hc(Ta-T)
(2)
(3)
式中:qc为热流密度,W/m2;hc为对流换热系数,m2·h·℃;Ta为大气温度,℃;T为桥梁结构表面温度,℃;v为结构表面风速,m/s。
桥梁结构的辐射换热按来源可分为吸收、反射两部分,吸收大气及地表辐射的热量,并向外辐射放热[10],总量可表示为
qr=al(Gαβ+Uαβ)-El
(4)
式中:qr为辐射换热总量,kJ;al为混凝土辐射吸收率;Gab为大气辐射热量,kJ;Uαβ为地表辐射热量,kJ;El为混凝土反射放热量,kJ。
2 工程实例与有限元模型
2.1 工程实例
本项目选取合福高铁上饶境内某32 m简支箱梁作为试验对象,该桥位于东经118°、北纬28°,桥梁方位角约9.5°。在箱梁与轨道结构中预埋了40个温度传感器,对该箱梁-轨道系统的温度场进行了2年以上的连续观测。温度数据采集利用预埋BGK-3700温度计作为测量元件,箱梁截面测点布置见图2。

图2 现场温度测点布置图(单位:cm)
2.2 有限元模型建立
利用有限元软件ANSYS的四边形单元PLANE55,对高速铁路箱梁温度场建模分析,模型参数取值见表1。

表1 箱梁温度场的有限元模型参数取值
箱梁温度场计算时间选取2020年12月27日-2021年1月1日,根据有限元软件分析,可得到1 d内不同时刻的箱梁温度场云图。以2021年1月1日为例,部分典型时刻的温度场分布云图见图3。


图3 2021年1月1日温度场云图(单位:℃)
2.3 模型验证
为验证该有限元模型的计算精度,以2020年12月27日-2021年1月1日为计算时间,选取代表性测点进行比较,对比结果如下。
图4为箱梁顶板测点的实测值与计算值对比,可以看出,两者峰值时刻吻合较好,变化趋势一致,最大差值均在2 ℃左右;19号测点的实测最高温度为13.8 ℃,计算最高温度为14.7 ℃,两者相差仅0.9 ℃。

图4 箱梁顶板19号测点计算值与实测值
由图4可见,有限元计算值的波动周期与实测值一致,发生时刻相同,温度场计算的渡越时间约为72 h,最大误差为1 ℃。本文建立的高速铁路箱梁日照温度场有限元模型可很好地模拟实际变化,计算精度可满足工程应用需要。
3 不同阶段的高速铁路箱梁温度场
3.1 裸梁阶段的箱梁温度场
建立裸梁阶段的箱梁日照温度场模型,相关参数取值同上,截面单元网格划分结果见图5。计算时间选取太阳辐射强且天气晴好的2021年8月1-6日,各关键点的温度-时间变化曲线见图6。

图5 裸梁阶段的箱梁温度场有限元模型

图6 裸梁阶段的箱梁顶板竖向温差
以顶板下缘为参考点的箱梁顶板存在较大的竖向温差,最大正温差出现在14:00附近,其值可达12 ℃,最大负温差为-6.9 ℃。对于裸梁阶段的箱梁顶板,顶板表面150 mm范围内,其传热现象较明显,温度变化较大。
3.2 铺设轨道后的箱梁温度场
合福高铁的轨道结构采用CRTS I型单元双块式轨道,单元式轨道可解决高温、严寒和大温差环境下轨道结构应力较高等问题,在我国武广客专、郑西客专、兰新客专、合福高铁等客运专线上得到广泛应用。铺设轨道后的箱梁温度场有限元模型见图7。

图7 铺设轨道后的箱梁温度场有限元模型
图8为受太阳直接辐射的箱梁顶板竖向温差。
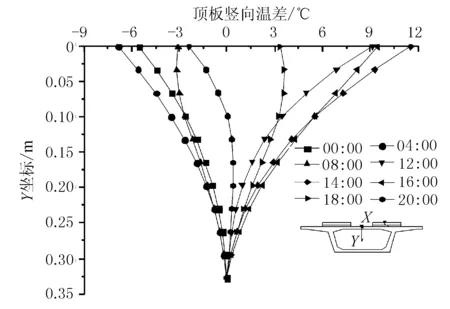
图8 受太阳直接辐射的箱梁顶板竖向温差
由图8可见,以顶板下缘为参考点的受太阳直接辐射的箱梁顶板存在较大的竖向温差,最大正温差出现在14:00附近,其值可达12 ℃,最大负温差为-6.9 ℃。
受轨道结构遮盖的箱梁顶板竖向温差较小,见图9,最大正温差出现在凌晨00:00附近,最大正温差仅为2.3 ℃;在14:00附近,受轨道遮盖的箱梁顶板竖向温度分布趋于一致。

图9 受轨道遮盖的箱梁顶板竖向温差
CRTS I型单元双块式轨道结构存在较大的竖向温差(见图10),最大正温差出现在14:00附近,最大值可达13 ℃以上,最大负温差为-5.3 ℃。在CRTS I型轨道结构表面150 mm范围内,轨道结构传热现象较明显,温度变化较大。

图10 轨道结构竖向温差
3.3 运营阶段的箱梁温度场
与铺设轨道阶段不同,运营阶段的高速铁路箱梁上建有防护墙、人行道板、栏杆、接触网立柱等附属设施,箱梁截面的温度分布规律也随之改变,运营阶段的箱梁温度场有限元模型及受附属设施遮盖的箱梁顶板竖向温差依次见图11、图12。

图11 运营阶段的箱梁温度场有限元模型

图12 受附属设施遮盖的箱梁顶板竖向温差
由图12可见,以顶板下缘为参考点的受附属设施遮盖的箱梁顶板竖向温差较小,最大正温差出现在凌晨04:00附近,其值可达2.8 ℃;最大负温差为-3.6 ℃,出现在16:00附近。附属设施遮盖对箱梁顶板的竖向温差影响较明显。

图13 受防护墙影响的轨道结构竖向温差
由图13可见,受防护墙影响的轨道结构存在较大的竖向温差,最大正温差出现在14:00附近,最大值可达11.3 ℃,最大负温差为-4.3 ℃。与轨道结构中心截面相比,受防护墙影响的轨道结构竖向温差较小。
4 不同阶段的箱梁温度梯度分布规律
4.1 箱梁的竖向温度梯度
根据上文所示的不同阶段箱梁顶板竖向温差图,以计算日(2021年8月6日)数据为研究对象,分析受太阳直接辐射、受轨道及附属设施遮盖的箱梁截面竖向温度梯度规律。选取箱梁截面正温差最大时刻,采用现有规范曲线:ty=t0eay对数据进行拟合,结果见图14。
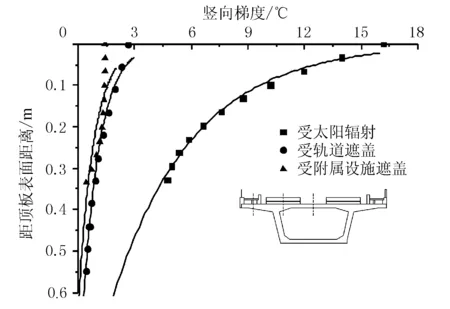
图14 箱梁不同截面的竖向温度梯度(升温)
升温模式下箱梁不同截面的竖向温度梯度与指数曲线的相关系数均大于0.9,箱梁截面的竖向温度梯度符合ty=t0eay指数规律,不同阶段箱梁截面的竖向梯度拟合系数(升温)见表2。
“部门联动”“一呼百应”“执法统一”……吴建生直言这三个词是“平安西江”建设中令他感到最欣喜的。“虽然广东海事局有统一的执法标准和规定,但是以前辖区各分支局在实际执法时的标准、执法力度各不相同,而且各分支局之间合作机制不完善,一旦发生事故,分支局与分支局的沟通交流也存在一定的障碍,通过共建‘平安西江’行动,这些问题统统都被解决了。”

表2 箱梁截面的竖向梯度拟合系数(升温)
由表2可见,升温模式下受太阳直接辐射的箱梁截面,其竖向温差t0达到16.48 ℃,远大于受遮盖的箱梁截面;随着受遮盖程度的增强,箱梁截面竖向温差t0逐渐降低,变化幅度较大。
同理选取箱梁截面负温差最大时刻,同样采用现有规范曲线ty=t0eay对数据进行拟合;由于被轨道遮盖的箱梁截面并不出现负温差,在此选取受太阳直接辐射、受附属设施遮盖的箱梁截面进行对比,结果见图15。

图15 箱梁不同截面的竖向温度梯度(降温)
由图15可见,降温模式下受太阳直接辐射的箱梁截面竖向温度梯度符合ty=t0eay指数规律;与升温模式相比,箱梁截面的竖向负温差在正温差基础上乘以-0.5,与JTG D60-2004 《中国公路桥涵设计通用规范》规定一致,箱梁截面的竖向梯度拟合系数(降温)见表3。

表3 箱梁截面的竖向梯度拟合系数(降温)
由表3可见,箱梁截面的竖向温度梯度满足:升温模式下,ty=16.48e-4.25y;降温模式下,ty=-7.92e-6.63y。
4.2 轨道结构的竖向温度梯度
根据上文所示的不同时刻轨道结构竖向温差图,以计算日(2021年8月6日)数据为研究对象,分析轨道结构竖向温度梯度规律,选取温差最大时刻,采用现有规范曲线ty=t0eay及双折线ty=t0+ay,对升温及降温数据进行拟合,结果见图16。

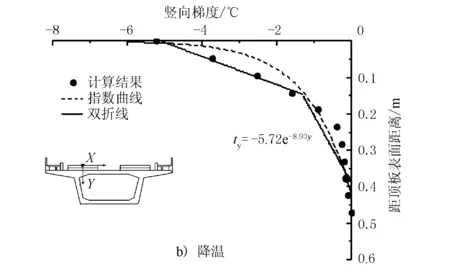
图16 轨道结构的竖向温度梯度
由图16可见,CRTS I型单元双块式轨道结构的竖向温度梯度满足:升温模式下,ty=14.26·e-7.72y;降温模式下,ty=-5.72e-8.93y。
4.3 箱梁的横向温度梯度
考虑到不同阶段轨道及附属设施对箱梁表面的遮盖效应,箱梁横向温度梯度主要体现在顶板表面。以计算日(2021年8月6日)数据为研究对象,分析不同阶段的箱梁顶板表面横向温度梯度,选取顶板表面横向温差最大时刻,结果见图17。

图17 箱梁顶板的横向温度梯度对比
由图17b)可见,裸梁阶段的箱梁顶板最大横向负温差仅为-1.5 ℃;对于铺设轨道及运营阶段的顶板表面,其最大负温差则均为-6.5 ℃。
对箱梁顶板的横向温度梯度进行多折线拟合,从偏安全角度出发,铺设轨道及运营阶段的顶板横向温差均取15.5 ℃,结果见图18。
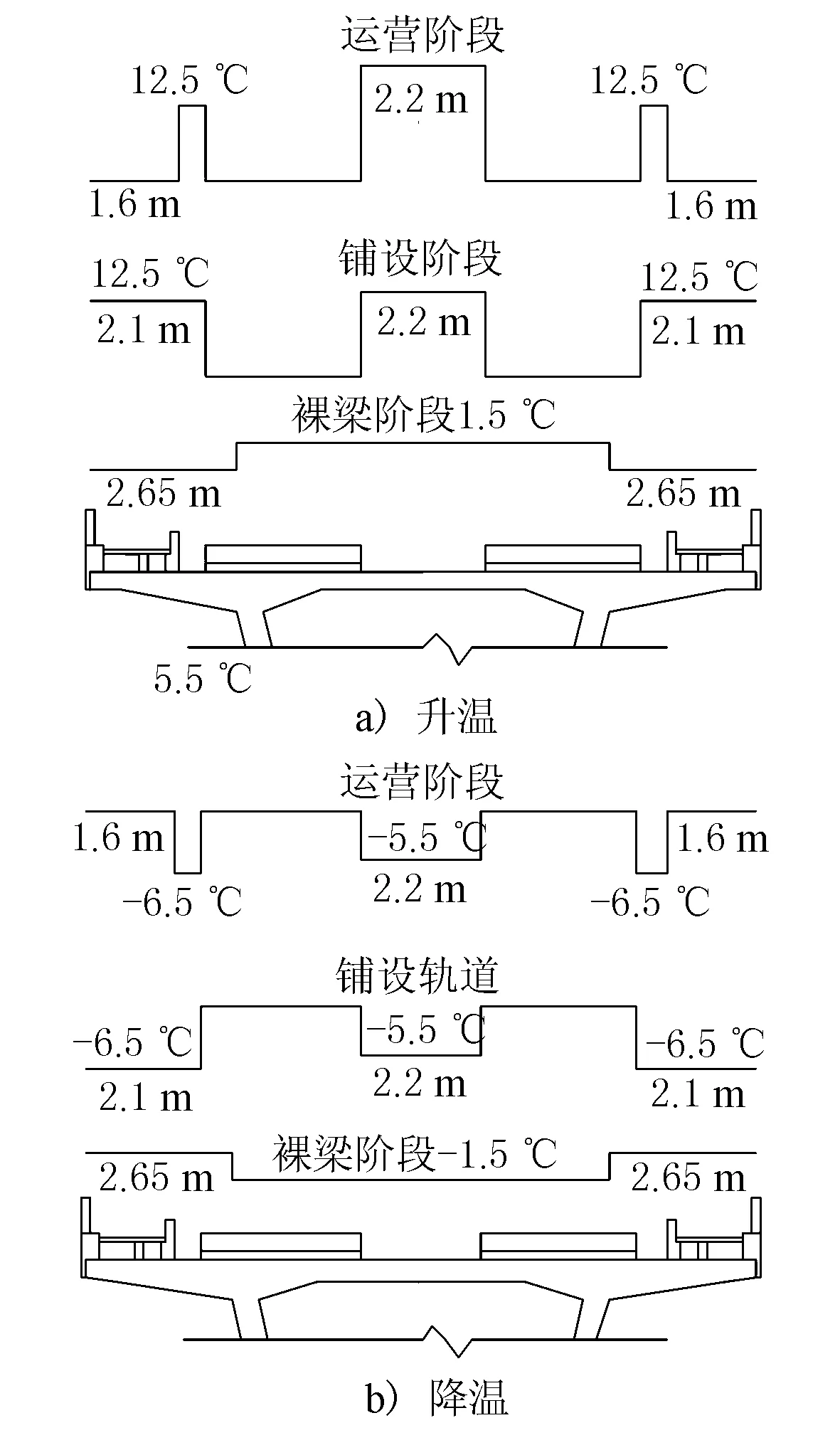
图18 箱梁顶板的横向温度梯度
5 结论
本文以合福高铁上饶32 m简支箱梁为工程背景,利用有限元仿真技术对高速铁路箱梁日照温度场进行数值模拟,得到以下主要结论。
1) 基于通用软件ANSYS平台,建立了高速铁路箱梁日照温度场有限元模型;通过与实测数据对比验证,指出箱梁温度场计算的渡越时间约为72 h,最大误差约为1 ℃,计算精度可满足工程应用需要。
2) 分别建立裸梁、铺设轨道及运营阶段的高速铁路箱梁日照温度场模型,计算结果表明:距离箱梁顶板表面150 mm范围内,其传热现象较明显;顶板最大正温差可达12 ℃以上,底板最大正温差仅为3.6 ℃;受太阳直接辐射的19号测点与受轨道及附属设施遮盖的16号、12号测点的最大温差分别可达11 ℃与13 ℃。
3) 总结不同阶段箱梁温度梯度分布规律,箱梁截面的竖向温度梯度满足:升温模式下,ty=16.48e-4.25y;降温模式下,ty=-7.92e-6.63y。考虑到轨道及附属设施对箱梁顶板表面的遮盖效应,分阶段提出箱梁顶板的横向温度梯度分布规律。

