永翠河流域1995—2014年降水对径流变化的影响

申智鹏，孙颖娜，胡金辉，姚 浩

(1.黑龙江大学水利电力学院;2.中俄寒区水文水利工程联合实验室，黑龙江 哈尔滨 150080)

在气候变化和人类经济活动的共同相互作用下，河川中的径流受到影响[1]。河川径流量决定了可用水资源的数量，河川径流和降水量变化决定了各个可用流域水资源的平均数量，近50年和100年的平均降水量周期变化不显著，但是不同年代际水量波动较大[2]。对人类的生活生产也带来了不同程度的影响，如农业灌溉、工业用水、居民用水等[3]，严重限制了社会和经济的发展。从水资源利用的角度来说，势必会影响永翠河流域的引水、用水，给下游居民带来不可避免的困扰。

针对上述问题，本文以永翠河1995—2014年的降水、径流资料，就降水对径流影响的贡献率和影响程度进行定量的分析计算，旨在为永翠河流域水资源的合理开发利用提供参考，为研究降水对径流的影响提供一种新的计算方式。

1 研究区概况

永翠河属山溪性河流，发源于寒月林场的翠源沟，属黑龙江，汤旺河水系，汇水面积677.0km2。其流域出口控制断面的水文测站为带岭(二)站，本文主要以带岭(二)站控制范围为典型区域，该站降水年内分配不均，多年平均降水为605.21mm，多年平均径流为323.99mm。

2 数据与方法

2.1 数据来源

主要数据分析摘自《黑龙江省水文年鉴》中国一带岭(二)观测站的逐日统计降水、径流观测资料，对数据进行规范、整理、计算得到时间序列为1995—2014年的20a资料。

2.2 研究方法

本文采用Mann-Kendall非参数检验法、累计距平法、积累曲线法、滑动平均法。利用M-K检验对降水和径流逐年进行α=0.05临界值显著水平检验，若UF曲线大于0，则表明序列呈上升趋势，若UF曲线小于0，则表明序列呈下降趋势。其中，α=0.05对应的统计量为正负1.96，称这个区间为置信区间。若序列统计量超过置信区间，表明序列变化显著。当UF与UB两条线的交点交于置信区间内，则该点对应的年份为突变的起始点。

累计距平法是判断序列的离散程度，通过观察曲线即可直接反映不同时期的径流与降水的变化情况。可用来检验M-K检验得到的突变年的准确性。确定突变年后可将时间分成2个时间序列，突变点前的时间称为基准年，突变点后的时间称为措施年[4]。

累积量斜率变化比较法[5]是根据累积曲线法进一步完善得到的方法，它可用于定量分析突变点前后对径流的贡献率。假设拐点年前径流为SRb，降水为SPb，拐点年后径流为SRa，降水为SPa，则降水对径流的贡献率可以表示为：

CP=(SPa/SPb-1)/(SRa/SRb-1)

(1)

3 降水、径流的变化特征及变化特征与突变

3.1 降水的年代际变化

研究区1995—2014年多年平均降雨量605.2mm，变差系数0.22。图1为用于研究该地区年内的降水距平及3a径流滑动平均线的变化幅度曲线。由图1可知，永翠河流域降水量有明显的年际变化周期特征。年平均降水量最大值出现在2012年，为828.1mm；最小值出现在2001年，为326.5mm。可看出降水年代际波动较大，1995—2014年呈现小幅上升趋势。

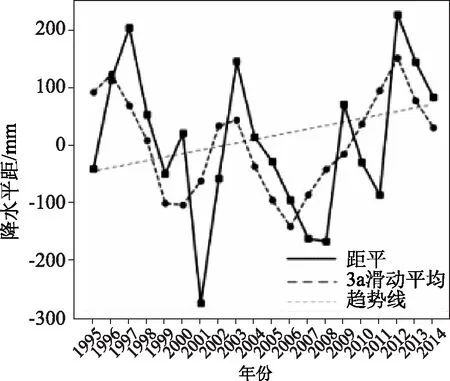
图1 降水距平与3a滑动平均图

3.2 径流的年代际变化

研究区1995—2014年多年平均径流深323.9mm，变差系数0.46。图2所示为用于研究该地区年内的径流深距平及3a径流滑动平均线的变化幅度曲线。由图2可知，永翠河流域径流量有明显的年际变化周期特征。年平均径流降水量最大出现在2013年，为631.3mm；最小最则出现在2001年，为126.2mm。可看出径流的年代际波动较同期降水波动更大，上升趋势较降水更显著，降水与径流的最大值出现的时间不同，可能存在流域调蓄作用，使径流的峰值出现滞后。

图2 径流距平与3a滑动平均图

3.3 降水与径流的突变

对永翠河流域进行降水-径流的相关分析，发现降水、径流在同步期内有着良好的一致性。由径流累积距平曲线图3所示，径流在1995—2014年有大幅波动，其中在2000—2002、2006—2008年间显著下降趋势；2008—2009、2012—2014年间有显著上升趋势。该时间段内最大值、最小值分别出现在2013年和2008年。且从2011年开始，呈现大幅度增长。拐点出现在1998年和2011年。用Man-Kendall法对永翠河1995—2014年平均径流进行突变检验分析，如图4所示。由图4可以看出，UF波动曲线在1995—1997、2002—2006、2008—2014三个时间段内主要呈波动上升的趋势。在1997—2002、2006—2008二个时间段内主要呈下降趋势，其中2个UF波动曲线在2011—2012年与UB曲线在置信区间内出现1个相交点(2011—2012年)。由此判断，径流在2011—2012年发生了由枯水到丰水的突变。

图3 永翠河1995—2014年年降雨量和径流累积距平曲线

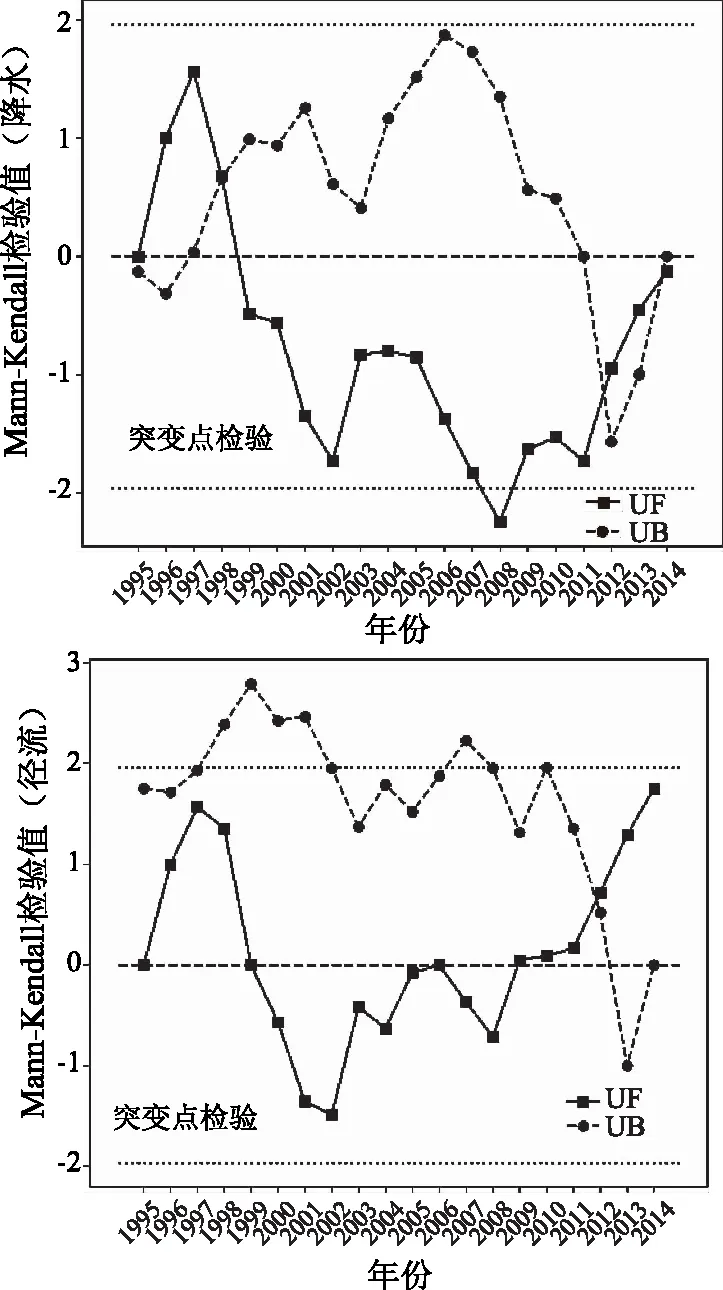
图4 永翠河年年降雨量和径流M-K法统计量(临界值显著性水平a=0.05)

降水累积距平曲线和Man-Kendall法对降水进行分析，UF和UB曲线在1995—2014年出现3个交点(1998年，2011—2012年，2013—2014年3个交点)，峰值出现在2013年，2011—2013年降水呈现增加趋势，则降水的突变发生在2011—2012年，降水由枯到丰的转变。

降水-径流双积累曲线图在突变点前后拟合度高，如图5所示。由图5可知，1998—1999和2010—2011年的左右拟合度最高，可得出径流的拐点年出现在1998—1999年和2011—2014年，又由降水和径流的M-K图可知，突变年为2011—1994年。基准年1995—2010年相关系数R2为0.994，突变年2011—2014年R2为0.992。基准年中人类活动影响较轻，因此影响径流的主要因素为气候变化;在措施年中，人类经济活动对其影响再度加剧，在气候变化和其他人类经济活动的共同影响下严重影响径流的变化[6]。

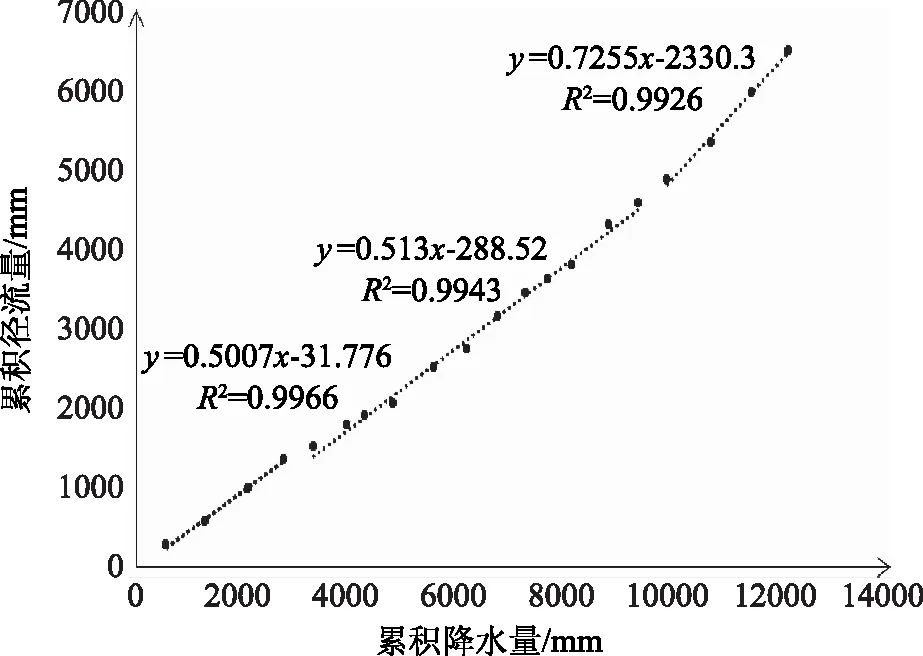
图5 降水-径流双积累曲线图

综上分析，永翠河流域1995—2014年中，基准年为1995—2010年，突变年为2011—2014年。

3.4 贡献率的分析计算

由降水、径流突变分析，确定2个拐点(其中1个拐点为突变点)，将累积降水、累积径流划分为3个时期1995—1998年，1999—2010年，2011—2014年分别命名为T1、T2、T3时期，如图6—7所示。

图6 降雨积累曲线

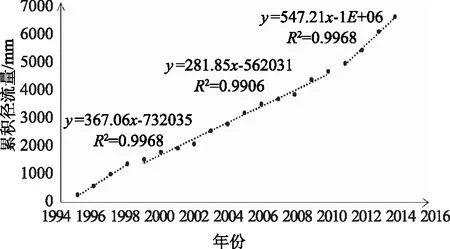
图7 径流积累曲线

T2与T1时期相比，累积径流斜率减少85.21mm/a，减小率为23.21%。同期累积降水斜率减少182.78mm/a，减小率为24.95%，见表1—2。这段时期对径流影响的因素为降水、蒸散发等气候变化。根据式(1)计算T2对T1时期降水对径流影响的贡献率超过100%，可能由于永翠河流域T1—T2时期中的部分流量来自融雪[6]，亦或存在地下水的补给，多种原因使得径流的来源不全为降水，导致T2对T1时期降水对径流的贡献率超过100%。

T3与T1时期相比，累积径流斜率增加180.15mm/a，增加率为49.08%。同期累积降水斜率增加19.46mm/a，增加率为2.66%，见表1—2。此时期对径流影响的因素为降水和人类活动影响。根据式(1)计算计算T3对T1时期降水对径流影响的贡献率为5.42%，T3时期处于突变年后，此时期人类活动逐渐加剧，降水对径流影响的比重降低。

T3与T2时期相比，累积径流斜率增加265.36mm/a，增加率为94.15%。同期累积降水斜率增加202.24mm/a，增加率为36.79%，见表1—2。根据式(1)计算T3对T1时期降水对径流影响的贡献率为39.08%。此时期为拐点与突变点的过度时期，降水对径流的影响较T1—T2时期小，较T1—T3时期大；人类活动影响较T1—T2时期小，较T1—T3时期大。

表1 累积降水斜率及变化率

表2 累积径流斜率及变化率

表3 回归模型(2)参数及检验结果

4 降水-径流多元逐步回归模型

4.1 逐步回归模型的建立

通过上述的突变分析，得到了基准年和突变年，分别建立回归模[7]。河道中的径流理论上全部来自降水，但是由于永翠河流域是典型的寒区，流域本身的调蓄作用使得河道中的径流存在一定的滞时，给方程的建立带来一定的困难。此次回归分析采用逐步回归模型，逐步回归模型是在回归模型的基础上，自动剔除不具显著性的自变量。当自变量较多，会按照自变量的显著性大小逐一引入模型，在进行回归分析，以提高模型的精确度。

4.2 逐步回归方程参数确定

本文尝试将资料划分为丰、平、枯3个时段，但由于资料序列长度无法满足建模需求，且划分时丰、平、枯时间序列会出现不连续的情况，改进后按水文年简单的将资料划分为丰、枯2个序列进行回归分析[8]。枯水期为11—4月，丰水期为5—12月。按照水文年划分后，将每年的枯水年与丰水年的径流、降水取平均值，作为因变量、自变量。为了充分利用资料，自变量中加入上年的降水，枯水年对应上年的丰水降水，丰水年对应上年的枯水降水。以P丰t、P枯t-1为自变量，R丰t为因变量建立丰水期的回归方程，以P枯t、P丰t-1为自变量，R枯t为因变量建立枯水期的回归方程，方程如下：

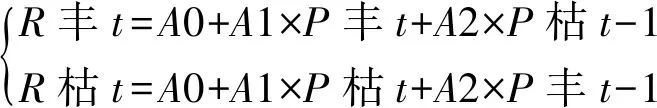
(2)

R2为相关系数，P为拒绝原假设的值，用以判断自变量的显著性。回归方程(2)中，时期1枯水期的R2小于0.5，拟合效果较差，无法满足拟合要求。丰水期加入上年的丰水降水P丰t-1，枯水期加入上一年的枯水降水P枯t-1，建立方程如下：

(3)

回归方程(3)中，时期1中的回归模型参数与方程(2)相同，但时期2中加入上述自变量后回归模型拟合度达到最佳。影响回归模型的因素很多，不能完全否定在时期1中加入1个自变量对模型没有影响，可能存在蒸发、下渗的因素影响使得模型前后的参数并没有发生变化。基于此情况，考虑永翠河流域的降水集中在6—8月，求得6—8月的平均值作为汛期，在丰水期加入P汛t-1，在枯水期加入P汛t作为第4个自变量，方程如下：

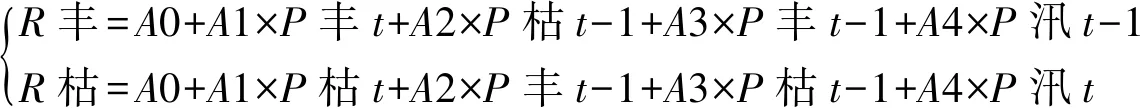
(4)

回归方程(4)中时期1的枯水年R2增大，时期2中的R2拟合度仍然最好，且所有R2>0.55，模型拟合度良好，方程(4)则为本流域的降水-径流多元逐步回归模型。

4.3 径流影响的定量分析

时期1为基础年，时期2为措施年。时期1的降水为P1丰、P1枯。时期2的降水为P2丰、P2枯。

将时期2中的降水P2丰、P2枯代入时期1的丰枯回归方程中，可以得到时期2的降水在时期1人类活动条件下的径流，与时期1的实测径流相比可以得到时期2条件下人类活动对径流的影响。2010—2011年丰、枯、汛期实测数据见表6，变化率见表7。

径流突变年前后(2010—2011年)，径流丰水期增长15.79%，枯水期减少28.84%。

表4 回归模型(3)参数及检验结果

表5 回归模型(4)参数及检验结果

表6 2010—2011年丰、枯、汛期实测数据 单位：mm

表7 丰、枯径流变化率

本文中，丰水期、枯水期方程中出现的时间角标不同是为了保证时间序列的连续；径流突变点后实测资料时间序列短，使得回归系数得1，会存在一定的误差。

5 结论与讨论

付军、冯平[8]使用动态回归模型，通过阈值确定丰、枯等自变量使模型拟合达到最优。以前人成果作为理论依据，提出将动态回归模型改进为逐步回归模型。逐步回归模型在动态回归模型的基础上增加了剔除不显著自变量的过程，在自变量的选择上通过不断尝试加入对径流有影响的雨期，用以提高模型的精度。

1995—2014年永翠河流域径流与降水均为增大趋势，趋势分析得到拐点年出现在1998年和2001年，突变检验确定突变年为2001年。逐步回归模型以本年的丰、枯水期、上年丰、枯水期，本年、上年的汛期做自变量逐一引入对应的方程发现精度在提高，但本文因资料缺突变年后的数据量较少，存在一定误差，且资料划分与自变量的确定过程较为繁琐，简化计算需要进一步讨论。