基于MIMO阵列的混合波束赋形算法
郑文逸,吴广富,李 云
(重庆邮电大学 通信与信息工程学院,重庆 400065)
0 引 言
低轨(low earth orbit,LEO)卫星通信系统具有传输链路损耗小、通信时延短、通信终端小、发射难度低等优点,被认为是最具潜力的卫星通信系统。在LEO互联网通信系统中使用频率为26.5~40 GHz的Ka波段,容易出现雨衰、阴影效应和多径效应[1]等现象,如图1所示。通过调整大规模多输入多输出(multiple input multiple output,MIMO)天线阵列中每根天线的加权系数,可产生具有指向性的波束,波束赋形可以补偿无线信号的衰落与失真,有效地提升通信系统的质量[2]。
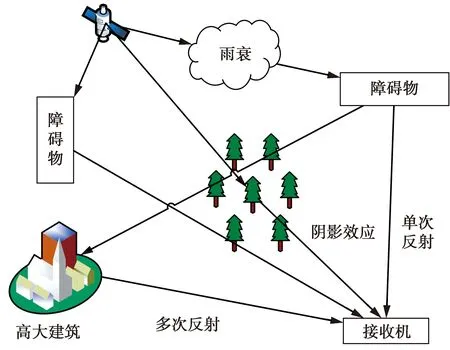
图1 低轨卫星信道传播图
波束赋形技术是一种基于大规模MIMO天线阵列的信号预处理技术,分为数字波束赋形(digital beamforming,DBF)[3]、模拟波束赋形(analog beamforming,ABF)[4]以及混合波束赋形(hybrid beamforming,HBF)[5]这3种架构。DBF架构通过处理数字信号调整发射信号的幅度和相位的权值,每一条射频(radio frequency,RF)链路需要一套独立的数模转换器、混频器、滤波器等器件,而每一条RF链路都需要和一根天线连接,因此,卫星通信中的发射天线数量会逐步增多,为了优化系统结构,减少硬件复杂度是有必要的;ABF架构则是对模拟信号进行处理,不要求RF链路与天线一一对应,但在通信性能方面会差于纯DBF架构;文献[5]结合DBF架构和ABF架构提出HBF架构,即在RF链路和天线阵列之间插入一个额外的模拟波束信号处理层,通过适当设计模拟波束矩阵减少RF链的数量。
基于上述HBF架构的算法需要在不同场景进行设计,通过与DBF算法的用户和速率进行对比来不断优化,达到更加接近DBF算法性能的目标。文献[6]基于DBF架构采用正则迫零波束赋形(regularized zero forcing beamforming,RZFB)在多用户通信系统中通过减少用户间的干扰来提升用户和速率、能耗效率等性能;文献[7]基于HBF架构提出模拟和数字混合编码方案,以用户和速率最大化、能耗效率最大化等为目标进行数学建模,通过少量迭代以提高用户和速率、能耗效率;对波束赋形的研究离不开信道状态信息,文献[8-9]利用非完善信道状态信息(imperfect channel state information,ICSI)进行卫星通信系统下的波束赋形研究,减轻信号干扰、降低噪声比,并最大程度降低发射功率消耗;文献[10]在已知全信道状态信息的情况下(channel state information,CSI),基于HBF架构采用广义正交匹配追踪算法,降低传统正交匹配追踪(orthogonal matching pursuit,OMP)算法的实现复杂度。
基于上述研究,本文提出了一种适用于LEO通信系统下HBF架构的串行遗传算法[11]。算法主要有种群模块、选择模块、交叉模块和变异模块。本文在已知CSI的基础上首先对LEO通信系统进行数学建模,对模拟域和数字域分别进行算法设计,然后在系统模型下对ABF矩阵和DBF矩阵串行迭代,得到最优HBF矩阵,使用户和速率、能耗效率最大化。与DBF架构下的算法和传统混合波束赋形架构下的OMP算法进行性能对比,结果表明,所提算法能更接近DBF的仿真性能,且硬件复杂度更低。
1 基于MIMO阵列的DBF系统
基于MIMO无线通信的DBF架构如图2所示,其中,H为信道信息。假设发射端有Nat根天线,与之配套的也有Nat根RF射频链路,LEO通信系统天线数量的增加导致发射硬件复杂度增高,使LEO通信系统中DBF架构的应用受到了限制。

图2 DBF架构图
假设接收天线数为Nar根,发送信号矩阵S为NS维的信息矩阵,NS为发送数据流个数,n表示Nar维的加性高斯白噪声,且服从方差为0、均值为σ2的噪声特征,则接收信号y为Nar维的信息矩阵,表示为
y=HS+n
(1)
在LEO通信场景中使用的频段为Ka波段,频谱为26.5~40 GHz,毫米波的频谱为30~300 GHz。Ka波段与毫米波有较多的交集,因此,本文基于Saleh-Valenzudel模型建立毫米波信道模型[12]。假设发射端与接收端之间存在Nd个散射器,信道模型表示为
(2)

(3)
(3)式中:λ是信号的波长;δ是相邻天线之间的间隔大小。
2 基于MIMO阵列的混合波束赋形算法
2.1 问题分析
基于MIMO阵列的下行HBF架构如图3所示。

图3 HBF架构图
相对于DBF架构,HBF架构在RF射频链路与天线阵列之间插入了一个额外的模拟信号处理层。图3中,NRF为RF射频链路的数量,Nat为发射天线的数量,NRF≤Nat,RF射频链路与发射天线数量不再要求一一对应。针对硬件上的改变,需要增加一个Nat×NRF维的模拟波束赋形矩阵FABF,同时FDBF矩阵也变成了NRF×NS维的矩阵,其接收信号表示为
y=HFABFFDBFS+n
(4)
通过对ABF矩阵和DBF矩阵的设计,能使LEO卫星通信在信噪比(signal to noise ratio,SNR)或信干噪比(signal to interference noise ratio,SINR)的约束下降低系统的能量消耗,或者在固定的功率下最大化用户和速率。在LEO卫星通信系统中,数字域可以通过波束赋形对矢量进行调整,达到幅度优化的目的;模拟部分则能使用放大器和移相器来调整矢量,提取幅度为系数,进行归一化处理,减少了放大器的使用,在一定程度上降低了开销。在单用户系统中用户和速率表示为
(5)
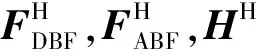
(6)
第k个用户的SINR表示为
(7)
用户和速率表示为
(8)
最大化用户和速率与ABF矩阵和DBF矩阵成正相关,因此,最大化用户和速率的问题转换为最大化FABF矩阵和FDBF矩阵,适应度函数为所设计算法的关键,恒模约束条件下适应度函数表示为
s.t. ‖FABFFDBF‖2=NS
(9)
LEO卫星通信系统中,一方面,需要提升用户和速率;另一方面,需要在有限的能耗中提升能耗效率。因此,能耗效率也是性能的重要体现,表示为
(10)
2.2 混合波束赋形算法
基于HBF架构下的波束赋形算法,采用启发式算法中的遗传算法,包含种群模块、选择模块、交叉模块以及变异模块;对ABF矩阵和DBF矩阵分别进行独立的迭代寻优,与二维的遗传算法相比,降低了算法复杂度;同时,又能通过相同的目标函数进行迭代联合。

在选择模块中采用轮盘赌算法。轮盘赌算法类似于俄罗斯轮盘赌游戏,在均匀的俄罗斯转盘随机选取获得一个数字,通过适应度值构成一个非均匀的轮盘,适应度值大则被选取的概率更大,适应度值由(9)式计算得出,然后根据概率统计公式统计出每个个体遗传到下一代群体中的概率,根据累积概率公式计算出每个个体的累积概率。随机生成M个随机数r∈[0,1],通过M次选择后得到新的群体。概率统计公式和累积概率公式分别表示为
(11)
Q(i)=Q(i-1)+P(i)
(12)

(13)
(13)式中,a,b∈[0,1]。进行多次重复交叉操作,获得交叉模块后新的群体。
在数字域中的交叉模块与模拟域的交叉模块在数学建模时会有所差别,分别表示为
(14)
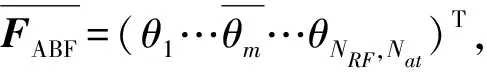
(15)

(16)
(16)式中,wUm和wLm分别是模值的最大值和最小值。
2.3 具体执行算法
串行遗传算法流程如图4所示。详细执行步骤如算法1所示。

图4 串行遗传算法流程图
算法1基于HBF的串行遗传算法
1)初始化仿真参数。终止代数T=40,迭代次数t=1,种群大小M=200,交叉概率P1=0.5,变异概率P2=0.1。
3)模拟域。
A:固定一组DBF矩阵FDBF=[w1,1…wn,m…wNRF,NS]T
B:根据FABFn,m=exp(jθn,m)计算FABF矩阵
C:轮盘赌选择模块
a)根据适应度函数(7)式和(9)式计算适应度值f(i),其中i=1,2,…,M;
b)根据适应度值f(i)以及统计函数(11)式计算存活概率P(i);
c)根据存活概率P(i)以及累积概率(12)式构建线性矩阵Q=[q1…qn…qM];
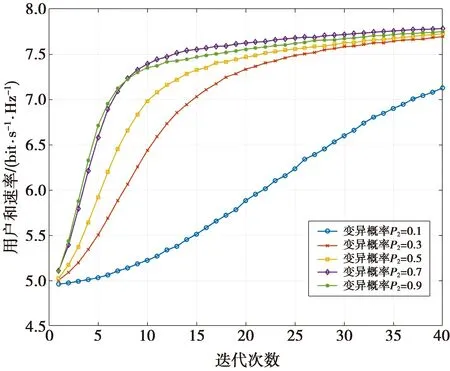
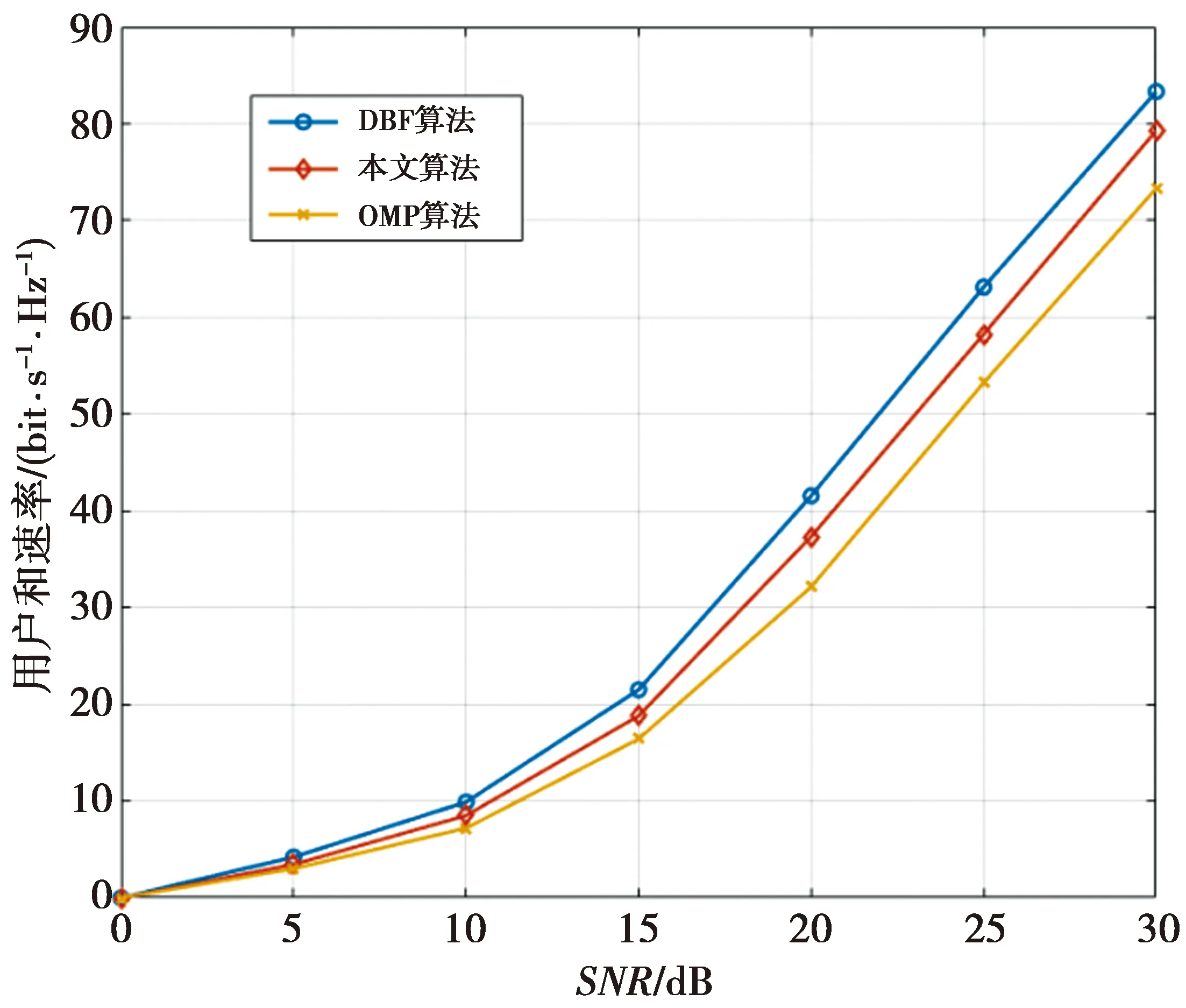
d)随机生成M个r∈[0,1],根据q[m-1] D:交叉模块 b)生成随机数r∈[0,1],判断r≤P1还是r>P1; d)若r>P1,rt=rt+1; E:变异模块 b)生成随机数r∈[0,1],判断r≤P2还是r>P2; c)若r≤P2,随机选择一个FABF,同时生成一个随机数v,根据(15)式进行计算,rt=rt+1; d)若r>P2,rt=rt+1; 4)数字域。 A:固定一组ABF矩阵FABF; B:同模拟域一样进行轮盘赌选择; C:类似于模拟域进行交叉算法; D:类似于模拟域进行变异算法。 5)通过适应度函数计算得出当代最优矩阵。 6)迭代次数t=t+1,若迭代次数等于终止代数终止循环,否则重复步骤3)、4)、5)。 设置系统仿真参数如表1所示。此外,RF射频链路数为8,发射数据流数为8,接收端为单天线用户。算法中设置初始种群规模大小为200,终止代数为40,交叉概率设置为0~1的常数,变异概率设置为0~1的常数。接下来在不同的天线数、交叉概率、变异概率下验证与对比研究算法的性能。从固定信噪比下最大化用户和速率、降低通信系统的能耗这2个维度进行性能验证。 表1 系统仿真参数 串行遗传算法中的交叉概率性能分析如图5所示。对发射天线数为128、接收天线数为1且用户数为1的单用户卫星通信系统,以用户和速率为目标函数的系统进行仿真。设置交叉概率分别为0.1、0.3、0.5、0.7、0.9且变异概率为0.1进行系统仿真,通过获得不同的收敛曲线找出其中的规律。从图5可以看出,随着交叉概率的增大,用户和速率逐渐收敛,增长速率越来越小。随着迭代次数的增加,用户和速率也在增加。前15次迭代后,用户和速率增长较快,到第25次迭代时趋于缓慢增长;在交叉概率为0.5时,用户和速率相对于初始状态提升了50.87%。除此之外,仿真系统的性能随着交叉概率的增长而提升;单独看第20次迭代时,随着交叉概率的增长,用户和速率的增长速率逐渐衰减。 图5 交叉概率性能分析图 对串行遗传算法中的变异概率性能分析如图6所示。对发射天线数为128、接收天线数为1、用户数为1的单用户卫星通信系统,以用户和速率为目标函数的系统进行仿真。设置变异概率分别为0.1、0.3、0.5、0.7、0.9且交叉概率为0.5进行系统的仿真,通过获得不同的收敛曲线找出其中的规律。随着变异概率的增大,用户和速率逐渐收敛,增长速率越来越小。随着迭代次数的增加,用户和速率也在增加。前10次迭代后,用户和速率增长较快,到第15次迭代时趋于缓慢增长。当变异概率为0.1时,在40次的迭代周期内不能达到收敛。同时变异概率与收敛速度并不是线性相关,此次仿真中,变异概率为0.7时性能最好。当变异概率为0.7时,在第15次迭代之前收敛速度较快,到第15次迭代时曲线缓慢增长,最终的用户和速率相对于初始状态提升52.37%。 图6 变异概率性能分析图 对LEO卫星通信系统中的能耗效率性能分析如图7所示。将变异概率设置为0.1,交叉概率为0.5,对接收天线数为1、用户数为1的单用户卫星通信系统,以能耗效率为目标函数的系统进行仿真。在相同的RF射频链路数和SNR为20 dB时,通过设置128、64、32这3种不同的发射天线数量,能耗效率通过串行遗传算法得到有效的增长。天线数量越多,能耗效率越大。随着迭代次数的增加,能耗效率也逐渐增长,但是其增长速率逐渐降低,趋近于0。在第25次迭代的时候趋于稳定。在发射天线数为128时,能耗效率相对于初始状态提升了53.57%。 图7 能耗效率性能分析图 基于串行遗传算法的第25次迭代结果,在不同的信噪比下,以用户和速率为目标函数进行仿真,结果如图8所示。图8中,变异概率设置为0.1,交叉概率为0.5,采用接收天线数为1且用户数为16的单用户卫星通信系统。由图8可见,无论何种算法,用户和速率都随着SNR增大而增大,且当SNR较小时区别较小。当SNR=30 dB时,所有算法性能均到达当前最优,且DBF算法性能最优,而本文所提算法相对于传统的OMP算法用户和速率提升了6.61%。 图8 信噪比和用户和速率 本文是基于大规模MIMO天线阵列的HBF算法研究,通过在不同的收发天线数和用户数的通信系统下进行仿真,验证了本文算法的用户和速率以及能耗效率性能。本文算法采用HBF的硬件架构,减少了RF射频链路,降低了硬件复杂度,其性能更接近于纯DBF的性能,相对于传统的OMP算法,用户和速率提升了6.61%。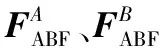


3 仿真分析



4 结束语

