一类带时滞的计算机病毒模型的最优控制

李小妮

（陕西国际商贸学院 通识学院，陕西 西安 712046）

0 引 言

病毒编制者将破坏计算机功能的数据、代码插入计算机内，从而构成了计算机病毒。与生物学中的病毒一样，计算机病毒在计算机内具有繁殖性、传染性、破坏性、潜伏性、隐蔽性、可激活再生性，计算机病毒的复制能力非常强大，是由如果计算机感染计算机病毒后，计算机能够快速地从一个用户到另一个用户蔓延开来，再加上计算机的迅速普及，这样更提高了计算机病毒传播能力，计算机病毒的爆发，对社会造成了负担，进而对人们的经济造成了巨大的影响，及时有效的防控措施显得尤为重要，近年来，许多学者建立数学模型对疾病传播规律进行研究，在预防、控制病毒传播方面发挥了重要作用。

计算机病毒传播规律与生物数学中流行病的传播类似，在生物数学中，政府、公共卫生机构鼓励民众进行相应的预防（如戴口罩、消毒、自我隔离等）是一种及时、低成本的防控措施，信息干预可以使疫情规模变小，降低流行病爆发的峰值，因此，在计算机病毒防护中，前期的宣传、提高人们的防护意识尤为重要。

另一方面，杀毒软件的应用也是一种直接有效的干预措施，有助于减轻人们的负担，控制病毒的传播.因此，杀毒措施可以更大程度地抑制病毒传播。

对于有关部门来说，适宜的实施计算机信息安全方面的宣传报道与杀毒软件的应用非常必要，将多种防控措施作为决策变量，联合起来效果更好，因此，许多学者将宣传报道、杀毒软件的应用等作为控制变量，研究计算机病毒模型，由于计算机病毒有相应的潜伏期，会出现各种形式的延迟，将时滞引入模型会更贴合实际，因此，越来越多的学者研究带时滞的计算机病毒模型。

因此，本文考虑将两种控制变量（计算机信息安全方面的宣传报道、杀毒软件的应用）和时滞引入计算机病毒模型中，研究带时滞的计算机病毒模型的最优控制问题，得到最优的控制策略。

1 模型的建立

计算机网络是由若干个计算机节点构成的，我们将这些计算机节点分为五类，分别是容易感染病毒的节点、暴露在外面的节点、已感染病毒但还未表现出来的节点、已感染病毒并表现出来的节点、应用计算机杀毒软件的节点、恢复到健康的节点，所有的计算机节点（包括容易感染病毒的节点、暴露在外面的节点）都会或多或少的受到恶意软件的攻击，当计算机感染病毒时，感染病毒的计算机节点会传染给其他健康的计算机节点，使得计算机病毒节点增加，进而形成计算机病毒。

为了描述计算机病毒的动力学行为，我们提出如下的计算机病毒传播模型：

其中，，I，I，I，分别代表易感节点、暴露节点、已感染病毒但还未表现出来的节点、已感染病毒并表现出来的节点、应用计算机杀毒软件的节点、恢复到健康的节点，模型（1）中所有非负参数的生物学意义为：，，，分别表示计算机的输入率、被病毒感染无法工作的比率、病毒感染系数、病毒感染的恢复率；β，β，β表示被病毒感染的比率；γ，γ，γ表示传染节点恢复到健康的比率；表示已表现出来症状节点与未表现出来症状的比率（0 ≤≤1）。

由于现实生活中，所有病毒都有潜伏期，所以我们将控制变量与时滞引入模型（1），得到带时滞的计算机病毒的最优控制模型：

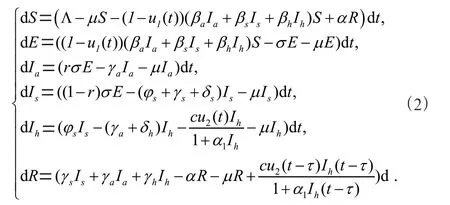
其中，（），（）分别表示宣传强度、杀毒强度；为饱和常数。

2 最优控制的存在性

本小节给出最优控制存在性的结果。

定理1：对系统（2），存在最优控制对=（，）∈及相关联的最优状态（，，I，I，I，），使得：

证明：

（1）控制变量（，）与控制状态变量非负；

（2）为凸紧集，（，，，，）为凸函数；

（3）最优系统是有界的；

（4）存在常数，，使得：

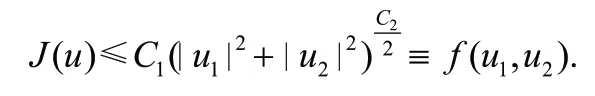
3 最优控制的刻画

本小节，首先构建 Hamilton 函数、利用 Pontryagins 最大值原理研究系统（2）的最优控制问题。

定理2：令，满足最优控制系统（2）的控制变量，，，I，I，I，为最优状态量，（）表示区间[，]上的示性函数，则存在伴随量（）=（，，，，，）∈R，满足如下伴随方程：

其中，λ（）=0（=1，2，3），相应的最优控制为：

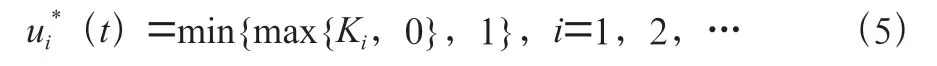
其中：

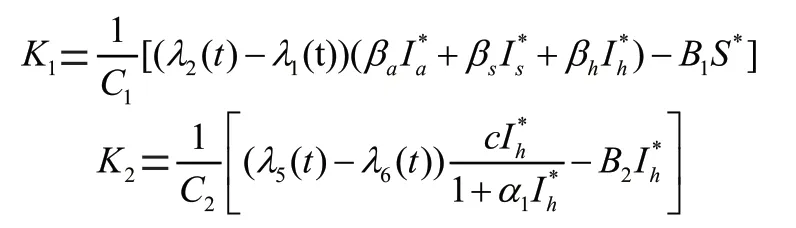
证明：为方便起见，令=（，，I，I，I，），（）=（，）且（）=（，，，，，），χ（）=（-），Hamilton 函数为：

令=（，）为系统（2）的最优控制，（）=（，，I，I，I，）T 为其相应的最优状态，由Pontryagins 最大值原理可知，存在（）∈R，使得最优控制存在的一阶必要条件可以表示为如下三部分：

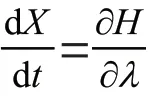
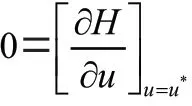
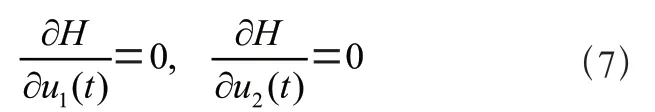
则由Hamilton 函数的表达式可得：

化简方程（8）可得：

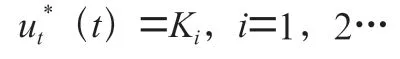
由控制变量u（）（=1，2）的有界性，可得方程（5）成立；

（3）伴随方程为

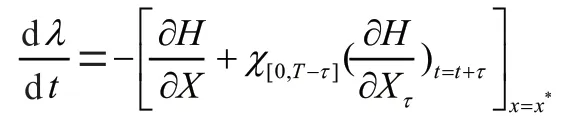
将（6）代入上式得到：

其中，λ（）=0（=1，2）为横截条件，证毕。

4 数值模拟

本节，我们对模型（2）进行数值模拟，模型（2）的参数取值如下：=100；Δ=0.01；=3.1；=5.48×10；β=0.761 1，β=0.192 5，β=0.016 7；=0.3；=1/5.1；=0.48；γ=1/5.1；γ=，φ=0.022 1；γ=1/10；δ=0.015；=；δ=0.04；=0.1，权重=0.15，=0.025，=0.01，=0.031，=0.01，=0.01，初始值=1 000，=50，I=10，I=10，I=10，=1。

数值模拟结果如图1所示。

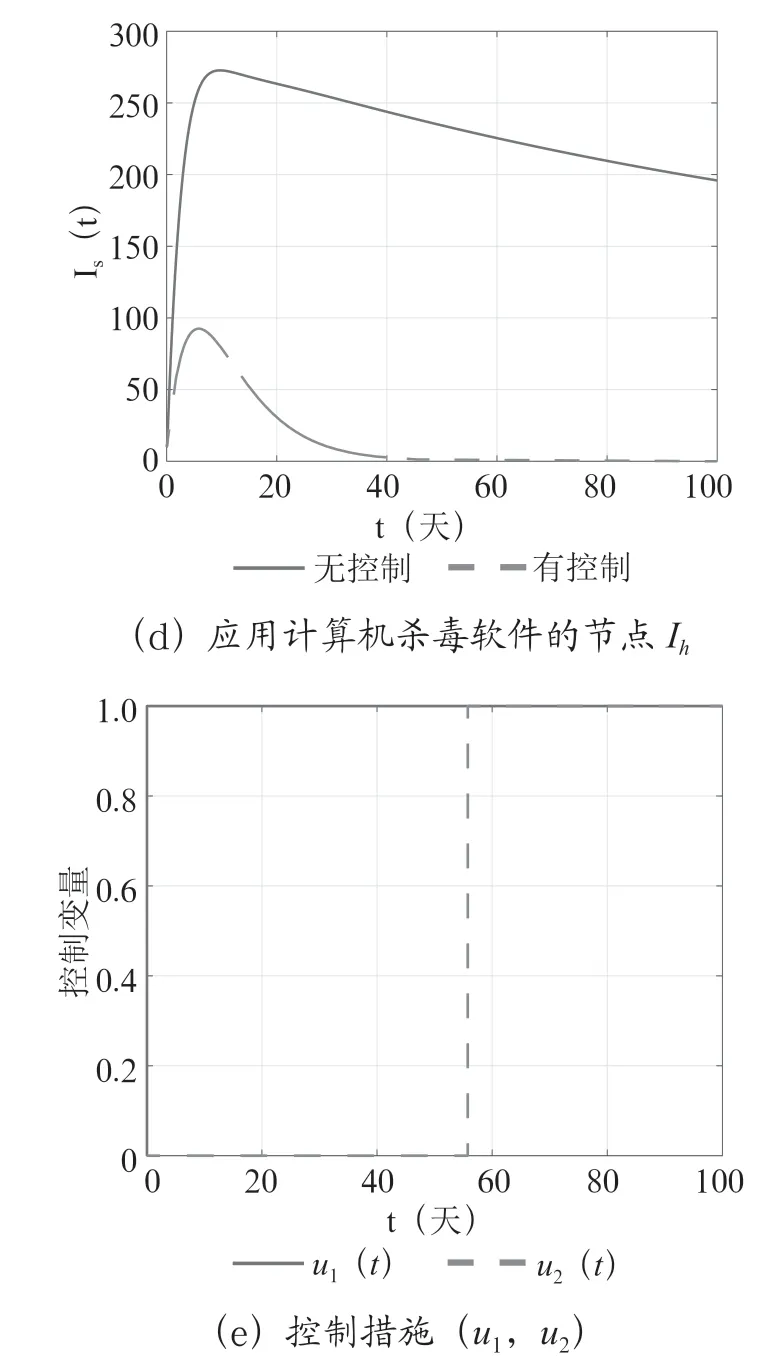
图1 最优控制与最优状态

图1给出了有无控制措施两种状态下的时间序列图，图1（a）给出了有控制措施、无控制措施两种情况下，计算机病毒的暴露节点的时间序列灭绝图。由图1（a）可以看出，实施控制措施后，能使暴露节点迅速减少半数以上。图1（b）给出了有控制措施、无控制措施两种情况下，计算机病毒的已感染病毒还未表现出来的节点I的时间序列灭绝图，由图1（b）可以看出，实施控制措施后，虽然在时间段0 ≤≤20 有一个小的上升，但在上升之后迅速减少，在30天前后，已感染病毒还未表现出来的节点I灭绝。图1（c）给出了有控制措施、无控制措施两种情况下，计算机病毒的已感染病毒且已表现出来的节点I的时间序列灭绝图，由图1（c）可以看出，实施控制措施后，在第10 天左右有一个小的波动，但在波动之后迅速减少，在40 天前后，已感染病毒且已表现出来的节点I灭绝。图1（d）给出了有控制措施、无控制措施两种情况下，计算机病毒的应用计算机杀毒软件的节点I的时间序列灭绝图.由图1（d）可以看出，实施控制措施后，虽然在时间段0 ≤≤5 呈现上升趋势，但在第5天左右迅速递减，在40 天前后，应用计算机杀毒软件的节点I灭绝。 图1（e）给出了两种控制措施，的取值情况。

综上所述，由图1可以看出，实施控制措施后，暴露节点、已感染病毒还未表现出来的节点I、已感染病毒且已表现出来的节点I、应用计算机杀毒软件的节点I都在时间段0 ≤≤20 之间存在拐点，并有着明显的下降，由此可以断定，两种控制措施对计算机病毒模型的防控具有重要的意义。

5 结 论

计算机病毒的传播、爆发给社会公民造成了困扰，增强人民计算机安全意识与杀毒软件的正确使用是抑制计算机病毒传播的重要措施。因此，本文主要研究的是一类带时滞的计算机病毒模型的最优控制问题。首先，我们对计算机病毒模型引入决策变量和时滞，建立了新的带时滞的计算机病毒模型的最优控制模型；其次，对该控制问题进行理论分析，给出了最优控制存在的一阶必要条件。最后，对理论结果进行数值模拟，数值模拟结果可以看出，同时采取宣传报道、杀毒软件的使用对抑制计算机病毒有更好的效果。