连续变量量子计算和量子纠错研究进展*
王美红 郝树宏 秦忠忠 苏晓龙†
1)(山西大学光电研究所,量子光学与光量子器件国家重点实验室,极端光学协同创新中心,太原 030006)
2)(安徽工业大学数理科学与工程学院,马鞍山 243000)
量子计算机在解决某些复杂问题方面具有经典计算机无法比拟的优势.实现大规模量子计算需建立具有通用性、可扩展性和容错性的硬件平台.连续变量光学系统具有独特的优势,是实现大规模量子计算的一种可行途径,近年来受到了广泛关注.基于测量的连续变量量子计算通过对大规模高斯簇态(cluster 态)的测量和测量结果的前馈来实现计算,为实现量子计算提供了一条可行的途径.量子纠错是量子计算和量子通信中保护量子信息的重要环节.本文简要介绍了基于cluster 态的单向量子计算、基于光学薛定谔猫态的量子计算和连续变量量子纠错的基本原理和研究进展,并讨论了连续变量量子计算面临的问题和挑战.
1 引言
量子计算机有望解决经典计算机无法完成的计算任务,在解决某些复杂问题方面(如大数分解[1]、量子模拟[2]等)相比经典计算机实现指数级别的加速.相比于经典计算机,量子计算机主要有并行性[3,4]和随机性[5]两大特点.鉴于量子计算的巨大潜在价值,世界各国积极整合研究力量和资源,开展了相关研究;同时,大型高科技公司如谷歌、微软、IBM等也纷纷介入量子计算研究.
研究表明,量子计算机的研制需要七个阶段[6]:1)对单个量子比特的运算;2)多量子比特的算法;3)用于纠错和控制的量子非破坏(quantum nondemolition,QND)测量;4)存储时间比量子比特退相干时间更长的逻辑存储器;5)对单个逻辑量子比特的运算;6)多个逻辑量子比特的算法;7)容错量子计算.完成这七个研究阶段,将实现具有通用性、可扩展性和容错性的大规模量子计算机.
目前,超导系统[7-10]、离子阱系统[11,12]、半导体量子点[13,14]和集成光学芯片[15,16]等不同系统在量子计算方面取得了极大的研究进展.例如,在超导系统中,2019 年,谷歌公开报道利用可编程超导量子比特的处理器制备了包含53 个量子比特量子计算原型机“悬铃木(Sycamore)”,其处理“量子随机线路取样”问题比经典超算快2 个数量级[17].2019 年初,中国科学技术大学潘建伟教授研究组[18]将一维阵列中的12 个超导量子比特应用到量子行走研究,为多体现象的模拟以及通用量子计算的研究奠定了基础.2021 年,该研究组先后成功构建了包含62 个量子比特和66 个量子比特的可编程超导量子计算原型机“祖冲之号”[9]和“祖冲之二号”[19],并分别演示了二维可编程量子行走和“量子随机线路取样”任务的快速求解.在光学系统中,中国科学技术大学潘建伟教授研究组[20]于2020 年构建了“九章”量子计算原型机,实现了“高斯玻色取样”任务的快速求解.根据现有理论,该量子计算系统处理高斯玻色采样的速度比目前最快的超级计算机快一百万亿倍.随后,该研究组构建了113 个光子144 模式的“九章二号”量子计算原型机[21].
然而,目前实际量子算法的执行仍然具有挑战性.实现大规模量子计算机需要实现通用、可扩展和容错的量子计算.由于光学系统不需要低温或真空环境,且具有与环境的相互作用较弱等优势,因此具有良好的可扩展性和容错性.量子信息科学根据所采用的量子系统本征态具有分离谱或是连续谱结构而划分为离散变量(describe variables,DV)与连续变量(continuous variables,CV)两类.离散变量编码在有限维希尔伯特空间,连续变量编码在无限维希尔伯特空间.基于DV和CV 系统的光量子信息处理各有优缺点,正在并行发展[22,23].离散变量系统使用光子的偏振和原子的自旋等编码信息,可以获得最大纠缠度,但纠缠的产生通常是概率性的.而连续变量系统通常使用光场的正交振幅和正交位相编码,其纠缠的产生是确定性的,但无法获得完美的纠缠[24,25].
鉴于连续变量在无限维空间编码信息的独特优势,近年来基于连续变量的量子计算引起了越来越多关注,如高斯玻色采样及其相关算法[26-29]、基于连续变量的量子机器学习[30-32]、和其他连续变量量子算法和模拟[33,34].本文简要介绍基于光场的连续变量量子计算和量子纠错的基本原理和研究进展.
2 连续变量量子逻辑门
2.1 连续变量


基于光场的连续变量量子信息处理通常将信息编码到光场的正交分量,通过对其进行操控和测量实现量子信息处理.光场的正交振幅和正交位相分量可以通过平衡零拍探测系统进行测量,其示意图如图1 所示.在平衡零拍测量中,待测信号光场和本地振荡光场在一个50∶50 分束器上耦合,然后将耦合后的两束光进入光电管进行测量.输出光场表示为

图1 平衡零拍探测系统示意图[36]Fig.1.Schematic of balance homodyne detection[36] .

其中第一项和第二项为光电流的直流部分.当本地光的能量足够大时,方程(5)的第三、四项可以忽略,输出光电流的起伏为
因此,通过改变相对位相ϕ,可以实现信号光场不同正交分量的测量.当ϕ0和ϕπ/2,光电流差分别表示为和即分别对应待测光场的正交振幅和正交位相分量.如果我们所测量的信号光为压缩光,为了测定压缩度,则需要确定与之相应的散粒噪声极限(shot noise limit,SNL).为此,实验中可以挡住信号光场(相当于输入真空场),则此时平衡零拍探测系统输出的光电流为真空场的噪声,即SNL.
2.2 量子逻辑门
量子逻辑门是实现量子计算的核心.离散变量量子计算以|0〉和|1〉作为计算基矢实现量子信息处理,其基本信息单元是量子比特(qubits);而连续变量量子计算将无限维希尔伯特空间的{|s〉x}s∈R作为计算基矢,其基本信息单元是量子模式(qumodes).表1 总结了离散变量和连续变量量子逻辑门的比较.连续变量量子逻辑门根据其哈密顿量的不同分为高斯量子逻辑门和非高斯量子逻辑门.哈密顿量为2 阶及其以下的为高斯量子逻辑门,反之则为非高斯量子逻辑门.高斯量子逻辑门将输入的高斯态变换为另一个高斯态.在高斯量子逻辑门的基础上至少增加一个非高斯操作即可实现通用量子计算.下面是几种典型的连续变量量子逻辑门.



图2 平移算符对量子态的作用效果[39]Fig.2.Effect of displacement operation on quantum state[39].


表1 离散变量和连续变量量子逻辑门的比较[37]Table 1.Comparison between quantum logical gates with describe variables and continuous variables[37].
当θπ 时,输入态变换为


单模和双模高斯门可以组合成任意多模高斯门.经过高斯逻辑门操作,输入态的正交分量呈现线性变换.然而高斯量子逻辑门仅能实现高斯运算,无法完成任意的幺正量子逻辑门操作.
8)非高斯量子逻辑门在任意高斯操作的基础上,至少增加一个非高斯操作即可实现通用量子计算,因此非高斯逻辑门是连续变量量子计算的一个关键组成部分[40,41].典型的非高斯逻辑门通常表示为,其中n≥3,t表示非线性相互作用.经过非高斯逻辑门操作后,输出态正交分量变换为

3 基于cluster 态的连续变量量子计算
3.1 基于测量的连续变量量子计算
量子计算有两种模型: 一种是量子线路模型,另一种是基于测量的量子计算模型,也被称为单向量子计算[42].单向量子计算基于大规模簇态(cluster态)执行测量,通过测量结果的前馈来实现量子计算.在光学系统中,量子比特的测量通常比基于量子线路模型的量子门更容易,并在特定cluster 态下仅使用单个量子比特测量可实现通用量子计算[43].因此,单向量子计算已经成为实现大规模光量子计算的一种重要模型.
Cluster 态是一种具有相邻相互作用的多体纠缠态[38,44],是单向量子计算[43,45,46]和量子网络[47-49]的基本量子资源.连续变量cluster 态的纠缠结构示意图如图3 所示,图中每个节点代表一个qumode,节点间的连接代表相邻节点相互作用.

图3 多组份cluster 态示意图 (a)四组份线性cluster态[45];(b)二维cluster态[45];(c)三维cluster态[45]Fig.3.Schematic of multipartite cluster entangled states:(a)Linear four-mode cluster state[45];(b)two-dimensional cluster state[45];(c)three-dimensional cluster state[45].
连续变量cluster 态的量子关联形式为[38,44]

式中,a∈G表示cluster 态所代表的图G(graphG)的节点[50],而模式b∈Na是与模式相连的邻点,表示额外噪声.具有方程(16)形式的多体纠缠态被称为连续变量cluster 态,方程(16)被称为nullifier.在理想压缩情况下,N模连续变量cluster态是各个模式正交分量线性叠加算符的零本征值态,即0 .由于一次测量仅破坏与其相邻节点间的相互作用,而其余模式间的纠缠仍然存在,因此cluster 态具有良好的纠缠保持特性.
利用光场不同自由度的复用技术可实现不同尺度cluster 态的实验制备.目前发展的复用技术主要包括空间、时间和频率复用技术.将实验获得的压缩态光场经过特定的分束器网络结构耦合,可以实现空间复用cluster 态的制备[51-54].山西大学在国际上首次实验制备了空间分离的连续变量四组份Greenberger-Horne-Zeilinger(GHZ)态和cluster态[51],进一步实验制备了空间分离的连续变量八组份cluster 态光场[54],扩展了连续变量cluster 态的尺度.空间复用可以方便的将本地操作作用到每个模式上,然而随着纠缠模式数目的增加,分束器网络结构将会越来越复杂.
光频梳技术被应用于制备频率复用连续变量cluster态[55].该方法通过光学参量放大器的共振频率模式实现频率复用.2014 年,Chen等[56]实现了最多60 个频率模式的cluster 态.Roslund等[57]和Cai等[58]分别制备了10 个和13 个独立频率模式的cluster 态.由于受到位相匹配带宽的影响,该方法产生的最大频率梳数目受到限制,且纠缠模式不易分离.
制备大尺度纠缠态的另一种方法是时间复用.2011 年,Menicucci[59]提出了利用时间复用制备任意尺度连续变量cluster 态的方法.2013 年,Yokoyama等[60]实验上实现了10000 个模式cluster 态的制备.随后扩展到100 万个光学模式的纠缠态[61].2019 年,日本Furusawa 研究组[62]和丹麦Anderson 研究组[63]分别在实验上成功制备了二维cluster 态.三维cluster 态是实现容错量子计算的一种重要量子资源[64,65].2020 年,Fukui等[66]提出了一种三维cluster态的产生方案,并展示该纠缠态对基于拓扑保护测量的量子计算中有限压缩度产生的模拟误差具有鲁棒性.
3.2 基于测量的连续变量量子计算研究进展
光量子计算的主要挑战是实现可以对量子态进行任意幺正变换的通用量子逻辑门.在实验中,高斯量子逻辑门的实现较为简单,如平移操作可以通过将输入态和有调制信号的辅助态在分束器上耦合实现,旋转操作和分束器操作可以仅通过使用线性光学元件实现.而非高斯量子逻辑门的实现较为复杂.
日本Furusawa 教授研究组实现了基于测量的压缩门[67]、QND门[68]、单向二次位相门[69]和可控位相门操作[70],并提出了利用四组份cluster态实现任意压缩操作的方案[71].我们基于连续变量四组份cluster 态,通过平衡零拍探测和电子学前馈系统,实验实现了连续变量可控X 量子逻辑操作[72].2014 年,我们实验演示了基于两组份纠缠光场的单模压缩操作和傅里叶变换,实现了基本的量子逻辑门单元,简化了实验方案、节省了量子资源[73].仅仅一个量子逻辑门无法实现真正的量子算法.一般,需要连续执行一系列量子逻辑门操作,才能实现量子算法.我们以连续变量六组份cluster 态光场为资源,实验实现了一个包含单模压缩门和可控位相门的连续变量量子逻辑门序列,展现了连续变量量子计算的可行性[74].
近年来,基于时间复用cluster 态的连续变量量子计算取得了重要进展.2021 年,Asavanant等[75]使用时间复用cluster 态实现了旋转和shear 等量子逻辑操作.同年,Larsen等[76]基于二维cluster态实验实现了一组量子逻辑门.
3.3 连续变量量子计算的通用性
1999 年,Lloyd和Braunstein[40]提出了用连续变量构建通用量子计算机的充要条件.2006 年,Menicucci等[43]提出在实现任意的多模高斯操作(Clifford 群的操作)的基础上,至少增加一个非高斯操作(非Clifford 操作)就可以实现通用量子计算.立方位相门是一种典型的非高斯门.2001 年,Gottesman等[77]提出了基于双模压缩真空和光子数分辨探测器实现立方位相门的方案,如图4(a)所示.首先,输入态|ψ 〉和三阶位相辅助态|γ 〉执行可控X操作后对量子态|γ 〉的正交振幅分量进行测量.然后,将测量的反馈到输入态的正交位相分量上最后,通过前馈shear 操作(-2mγ)和平移操作Z(-m2γ)消除 2和m2γ项.因此输出态表示为

非高斯辅助态对立方位相门的实现非常重要.2016 年,Miyata等[78]提出通过自适应非高斯测量实现量子立方门,该方法需要制备立方位相态(cubic phase state).2018 年,Sabapathy和Weedbrook[79]提出通过使用压缩态、分束器耦合BS、平移操作Z和依赖于单光子计数结果的压缩操作,可实现三阶立方位相门辅助态|γ 〉的制备,其制备线路图如图4(b)所示.然而,该方案对压缩度提出较高的要求.而Fock 态的叠加可以被看作是立方位相态.目前,弱立方位相态|0〉+c|1&3〉已经被实验制备[80].
3.4 连续变量量子计算的可扩展性
构建量子计算机需要扩展量子计算机的规模,大规模量子计算机的实现需要有效增加量子比特数.增加量子比特数目的一种方法是基于时间复用连续变量cluster 态实现量子计算.目前,采用该方法已经能够产生纠缠模式大于10000 的连续变量cluster态[60-63],并且正在开展量子逻辑门研究[75,76].
增加量子比特数目的另一种方法是采用集成光学芯片实现大规模量子计算.目前实现的连续变量集成光学芯片主要基于氧化硅、氮化硅和铌酸锂(lithium niobate,LiNbO3)三种材料.在氧化硅集成光学芯片方面,Furusawa 研究组[81]实现了芯片上连续变量两组份纠缠态的制备.最近,美国弗吉尼亚大学实现了压缩态光场和20 对双模压缩态光场的制备[82].在氮化硅集成光学芯片方面,已经实现了最高—1.70 dB 压缩态光场的制备[83-85].2021 年,加拿大Zhang等[86]将微环腔和线路集成在一起,实现了片上的高斯玻色采样、分子振动光谱和图形相似性的计算[15].在铌酸锂集成光学芯片方面,已经实验实现了压缩态光场[87,88]和双模纠缠态的产生和表征[89].2020 年,Yi等[90]和Chen等[91]基于LiNbO3的集成光学芯片实现了量子态的产生和操控.
4 基于光学猫态的量子计算
4.1 基本原理
在量子计算中,量子态的叠加原理使得量子计算机在处理某些复杂问题时能够具有经典计算机无法替代的优势.薛定谔猫态不仅可以用于探索经典和量子物理的边界[92-94],还可以用于量子计算、量子隐形传态和精密测量[95-98].光学薛定谔猫态是两个幅度相同、位相相反相干态的叠加,被定义为其中N±ϕ0 对应于偶猫态,仅包含偶数项光子.ϕπ 对应于奇猫态仅含有奇数项光子.两个相干态的重叠度为|〈α|-α〉|2光学薛定谔猫态是一种非高斯态,可以通过对一个高斯态作用非高斯操作实现.实验上可以通过从压缩真空态中减去光子产生,减去奇数个光子制备奇猫态,或者减去偶数个光子制备偶猫态[99].国际上已经有多个研究组基于此方案成功的产生了尺度较小的光学薛定谔猫态[100-103].
光学薛定谔猫态是相干叠加态,可以做为量子比特应用于量子计算中.当以相干态为基矢来编码qubit 时,光学薛定谔猫态中的|-α〉被编码为|0〉L,|α〉被编码为|1〉L.基于光学猫态的量子计算要求两个相干态几乎正交,即重叠部分几乎为零.当|α|2 时,两个相干态的重叠部分≈10-7,也就是说|〈α|-α〉|2≈0 .所以产生α≥2 的光学薛定谔猫态在连续变量量子信息处理中有重要意义[95].下面我们介绍基于光学猫态的几种典型量子逻辑门.
1)Bit-flip门也称为X门.Bit-flip 门表示为它的作用效果为X(µ|-α〉+v|α〉)µ|α〉+ν|-α〉.该逻辑门可以通过将输入态相对于本地振荡延迟半个周期来翻转实现[95].
2)Phase-flip门也称为Z门.Phase-flip 门的作用效果为对输入比特进行位相反转操作Z(µ|-α〉+v|α〉)µ|-α〉-v|α〉.实现phaseflip 门的方案如下[95].将输入态µ|-α〉+v|α〉和Bell 纠缠猫态 (|-α,-α〉+|α,α〉)/一个模式耦合后进行Bell 态测量,并将测量结果反馈至Bell纠缠猫态的另一个模式,得到四种输出结果: 1)µ|-α 〉+ν|α 〉; 2)µ|-α 〉-v|α 〉;3)µ|α 〉+ν|-α 〉;4)µ|α〉-v|-α 〉.通过使用bit-flip 操作可将3)和4)的错误反转纠正为3)µ|-α 〉+ν|α 〉,4)µ|-α〉-v|α 〉.因此,在纠正错误后,得到两种输出结果:1)和3)情况下输入结果不变,2)和4)情况下输入比特发生位相反转操作.
3)Hadamard门相干态|±α〉经过Hadamard门操作后转换为.实现Hadamard 门的方案如图5 所示[104].经过平移操作的输入态和辅助态分别经过低反射率分束器 B Su后,反射部分在分束器BSΓ实现不可区分的减光子操作当输入态的透射部分在单光子探测器有响应时,即可实现Hadamard 门变换.

图5 基于光学猫态的Hadamard 门方案示意图[104]Fig.5.Schematic of Hadamard gate based on optical cat state[104].
4)Phase rotation gate门实现位相旋转门(phase rotation gate)的方案如图6 所示[95].首先将输入态沿着相空间的虚轴(正交位相方向)做微小平移其输入态变换为

图6 基于光学猫态的位相旋转门方案示意图[95]Fig.6.Schematic of phase rotation gate based on optical cat state[95].

然后将平移后的量子态和Bell 猫态的一个模式进行联合测量,并将测量结果经过X门操作和Z操作纠正后,得到的输出态为
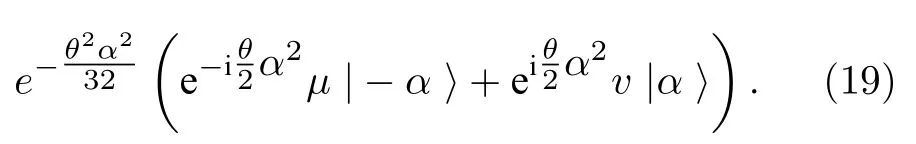
其效果为围绕Z轴旋转θ.
5)可控位相门可控位相门是一种重要的两比特量子逻辑门.基于光学猫态实现可控位相门的原理图如图7 所示[95].首先将输入的两个量子态:

图7 基于光学猫态的可控位相门方案示意图[95]Fig.7.Schematic of controlled phase gate based on optical cat state[95].
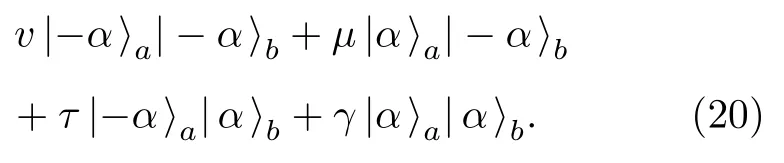
在分束器上耦合,然后分束器的两个输出态分别和纠缠猫态的一个模式进行Bell 测量,并将测量的结果经过X操作和Z操作进行错误纠正后得到最终的输出态

输出态的正负号由Bell 测量的输出结果决定.如果选择ϕ2θα2π/2,该方案即可实现等价于可控X量子逻辑门.
4.2 研究进展
2003 年,Ralph等[95]理论上提出了利用相干叠加态实现单模和双模量子逻辑门的方案.随后,研究表明相干叠加态可以实现容错量子计算[97],并进一步提出了单模位相门、双模位相门、双模受控位相门以及单模Hadamard 逻辑门的实验方案[104].2011 年,丹麦Andersen 研究组[105]利用相干叠加态作为量子比特,实现了Hadamard 量子逻辑门.2012 年,法国Grangier 研究组[106]利用减光子操作将一个奇猫态转化为偶猫态,实现了π相移的量子逻辑门.
目前,实验中实现的基于光学猫态的量子逻辑门局限于单模逻辑门,双模量子逻辑门的实现仍然具有挑战性.要想实现双模逻辑门,首先需要制备纠缠猫态(Bell-cat).实验上制备光学Bell 猫态的方法有两种: 1)将两个压缩真空态在减光子部分建立纠缠,对其中一束光进行光子计数.Grangier研究组[107]和Lvovsky 研究组[108]通过该方法分别制备了Bell 猫态.2)直接将薛定谔猫态与真空态在50:50 分束器上耦合,产生Bell 猫态.此方案中Bell 猫态的产率仅取决于薛定谔猫态本身的产率,但对应Bell 猫态的尺度将会降低倍.
5 连续变量量子纠错
量子态受到环境中损耗和噪声等因素的影响会导致退相干效应,从而使得最终输出态和输入态之前存在误差.这些误差会破坏相干性,降低量子计算的计算能力.因此,量子纠错是实现高保真度量子信息处理的一个关键环节.
5.1 玻色子码
在连续变量量子纠错中,玻色子码(Bosonic code)是常用的一种纠错码.玻色子码将离散的量子信息编码到玻色子模式[37],它能够纠正由于环境损耗引入的误差,从而保护量子信息.连续变量量子纠错码有多种玻色子码,包括九波包编码[109,110]、五波包编码[111,112]、Gottesman Kitaev Preskil(GKP)码[77]、纠缠辅助编码[113]和量子擦除(quantum erasure)方案[114]等.
研究表明高斯误差是不能通过纯高斯操作来实现量子纠错[115].然而,对于非高斯类型的误差,可以利用分束器网络的结构对输入模式进行编码,通过耦合适当的辅助模式来实现纠错[112].在连续变量量子纠错中,多种不同结构的纠正单一非高斯误差的九波包编码连续变量量子纠错[116]、量子擦除纠错方案[114]、关联信道纠错方案[117]和五波包编码量子纠错[118]已经被实验实现.研究表明对于高斯噪声引入的误差可以通过光子计数进行非高斯操作来实现量子纠错[119].
5.1.1 五波包编码量子纠错
与九波包编码量子纠错相比,五波包编码量子纠错能够节省量子资源,高效的实现量子纠错.1998 年 Braunstein[111]提出了利用五波包结构高效地实现量子纠错编码的方案.2010 年,Walker和Braunstein[112]通过使用新的数学算法演示了一种可用于五波包量子纠错编码的线性光学网络结构.2015 年,Hao 等实现了纠正单一随机误差的五波包编码连续变量量子纠错[118].在该编码方案中,采用五模连续变量的纠缠态光场进行编码.值得注意的是,输入态的信息仅仅被编码在五个传输信道的其中三个信道,剩余的两个信道引入的误差不会影响输出态的结果,即输出量子态对这两个信道上的误差有免疫功能.其实验装置图如图8 所示,采用了真空态和压缩态光场作为输入信号,验证了任意的单一误差的量子纠错过程,而且输出态的保真度高于相应的经典极限.

图8 基于五波包部分编码方式的连续变量量子纠错方案[118]Fig.8.Scheme of CV quantum error correction with five-wave-packet code [118].
5.1.2 GKP码
2001 年,Gottesman等[77]提出一种GKP 码的编码方式,可用于实现通用和容错连续变量量子计算.随后,研究表明GKP 魔术态结合高斯操作和高斯测量可以实现通用量子计算[37].因此GKP编码提供了一种实现通用量子计算的有效途径.当正交振幅和正交位相分量发生小于纠错阈值的平移误差时,采用GKP 码作为纠错量子线路的辅助态,结合可控X门可分别实现对正交振幅和正交位相分量的量子纠错[120].此外,相比于基于猫态的量子计算,GKP 编码具有良好的容错性和对抗噪声能力[121].
通过将连续变量无限维希尔伯特空间转换为有限维的编码空间,产生GKP 量子比特.具体而言,GKP 码将量子比特编码到谐振子的正交振幅和正交位相分量,如图9 所示.理想情况下(无限压缩),GKP 码的逻辑和逻辑分别表示为
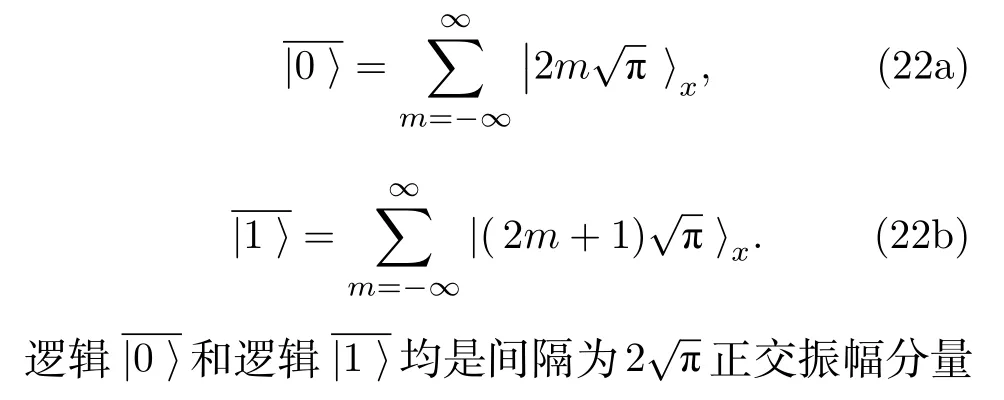

图9 GKP 量子比特的编码方式[77]Fig.9.The codeword for the GKP qubit[77].

目前,超导系统[122]和离子阱系统[123]已经实现了GKP 量子比特的制备.在光学系统中,几种GKP 码的制备方案已经被提出,例如迭代方法[124]和基于可分辨光子数探测器的高斯玻色采样[125,126]等.在迭代方案中,两个压缩猫态在一个分束器上耦合,并对一个输出端口的正交位相分量进行平衡零拍测量.当测量结果接近0 时,另一个端口为近似的GKP 量子比特.重复以上迭代过程可以不断增加GKP 量子比特中的高斯峰的数目[124].在基于可分辨光子数探测器的高斯玻色采样方案中,首先对输入的真空态分别进行平移和压缩操作,然后通过分束器网络干涉,最后对输出态进行可分辨光子数测量[126].迄今为止,光学系统GKP 量子比特的实验实现仍是一个挑战性问题.
5.2 拓扑码
拓扑纠错可以有效地修正量子计算中的误差,使得量子计算可以在高误差阈值和高容错率前提下被执行.研究表明,在量子纠错和容错量子计算中,对三维cluster 态进行适当的操控就能实现量子算法[64,65,127].基于cluster 态的拓扑性质,可以实现拓扑量子计算和拓扑误差修正[127-129].2020 年,Fukui等[66]提出了对有限压缩度产生的模拟误差具有鲁棒性的三维cluster 态产生方案.
近年来,一些与连续变量拓扑量子计算有关的基本概念已经被提出,例如任意子统计[130]、图形演化[50]、拓扑码[131]及其在量子通信中的应用[132]、基于任意子的连续变量量子计算[133]和容错量子计算[97,134].2021 年,Hao等[135]提出了基于八组份高斯cluster 态的连续变量拓扑纠错方案,方案如图10所示.首先,该方案提出了拓扑结构连续变量八组份纠缠态的产生方案,然后设计了连续变量拓扑纠错方案.当单个平移误差发生在任意一个模式和某两个模式时,双模的拓扑量子关联可以纠正误差.更有趣的是,与离散变量的拓扑纠错方案不同,当特定组合的三个模式发生相同的误差时,该方案仍可以有效地识别和纠正这些误差.

图10 基于cluster 态的连续变量拓扑误差修正方案 (a)八组份拓扑结构连续变量cluster 纠缠态的图态表示[135];(b)产生八组份连续变量cluster 纠缠态的分束器网络[135]Fig.10.Scheme of topological error correction with CV a Gaussian cluster state: (a)The graph structure of the topological eightpartite CV cluster state;(b)the beam-splitter network for the preparation of the cluster state[135].
6 总结讨论
综上所述,连续变量量子计算以其独特的优势为实现可扩展、通用和容错的量子计算机提供了一条可行途径.经过多年的发展,已经实现了大尺度cluster 态的实验制备和一系列高斯量子逻辑门,展现了连续变量量子计算的可行性.然而,面向可实用的大规模量子计算,仍然有一系列挑战性问题需要解决.在量子计算的通用性方面,非高斯量子逻辑门是通用量子计算的重要组成部分.目前光学系统中制备非高斯量子逻辑门的理论方案已经被提出,但非高斯量子逻辑门的实验实现仍然是连续变量量子计算的挑战之一.在量子计算的可扩展性方面,纠缠模式大于10000 的连续变量cluster 态已经被制备,为实现大规模量子计算提供了量子资源.然而,随着光学模式数和操作步骤的增加,需要的光学元件数目和占用的空间增加,因此急需发展连续变量集成光学芯片.目前已经实现了基于集成光学芯片压缩态和纠缠态的制备和操控,但基于集成光学芯片的量子逻辑门是实现可扩展量子计算的一个挑战.在量子计算的容错性方面,玻色子码和拓扑码是最常用的量子纠错码.GKP 码是一种较有优势的玻色子码,但光学系统GKP 码的制备和容错量子计算仍然具有挑战性.
本文简要介绍了近年来基于cluster 态的连续变量量子计算、基于光学薛定谔猫态的量子计算和连续变量量子纠错的基本原理和研究进展,并分析了实现大规模容错连续变量量子计算所面临的挑战.时间复用技术提供了连续变量量子计算所需的大尺度量子资源,为解决可扩展性问题提供了一条有效途径.集成光学芯片可以解决自由空间尺寸限制的问题,为连续变量量子计算的可扩展性提供了另一条可行途径,是发展实用化量子计算的必然趋势.GKP 码为实现通用性和容错性量子计算提供了可行的解决方案.虽然仍有一系列挑战性问题亟待解决,连续变量量子计算已经展现了独特的优势,例如“九章”量子计算原型机展示了解决高斯玻色采样难题的优势,具有广阔的发展前景.

