基于级联四波混频过程产生四模簇态*
董安琪 张凯† 荆杰泰2)3)‡ 刘伍明
1)(华东师范大学,精密光谱科学与技术国家重点实验室,上海 200062)
2)(中国科学院超强激光科学卓越创新中心,上海 201800)
3)(山西大学,极端光学协同创新中心,太原 030006)
4)(中国科学院物理研究所,北京凝聚态物理国家研究中心,北京 100190)
5)(中国科学院大学物理科学学院,北京 100190)
6)(松山湖材料实验室,东莞 523808)
簇态是量子计算和量子信息处理的重要资源,因其具有独特的纠缠性质和丰富的结构而受到广泛的关注.本文从理论上提出一种基于级联四波混频过程产生四模纠缠态的方案,利用部分转置正定判据和本征模分解研究其内部纠缠特性.此外,通过调控平衡零拍探测的相对相位和后处理噪声信号,将输出的纠缠态重构优化,最终生成三种不同结构的四模簇态.该方法可以有效地减少在有限的压缩条件下产生簇态而引入的额外噪声.本文理论结果为基于原子系综四波混频过程产生可扩展的连续变量簇态提供可靠方案.
1 引言
连续变量簇态作为一种重要的物理资源,在基于测量的量子计算和量子信息处理领域起着至关重要的作用[1].为了在真实物理系统中实现可扩展的量子计算,研究者们已经在理论上提出多种方案,并且在不同系统中进行了实验,其中单向量子计算机是基于测量的量子计算的重要理论框架[2],因此,簇态作为单向量子计算的基本资源而得到广泛的关注.依据特定的顺序和测量基矢对簇态做单模测量就可以实现量子计算[3].在连续变量系统中,通常使用线性分束器网络耦合多个独立的单模压缩态来构造连续变量簇态[4,5].然而,随着纠缠模式数的增加系统的复杂性也急剧增加.目前最新研究趋势是通过空间[6]、时间[7-9]和频率[10,11]复用多个非线性过程形成量子网络,这些方法产生的簇态适用于量子计算,但是由于产生的光束不易空间分离,所以很难应用在量子通信网络.因此,需要一种可扩展的确定性产生的方法生成空间分离的簇态.
基于热铷原子系综的四波混频(four-wave mixing,FWM)过程由于其独特的优势,已经证明是量子信息处理的重要资源[12-16].该系统由于原子相干特性而具有很强的非线性效应,使系统不需要借助光学腔而具有空间多模性,因此产生空间分离的非经典光束[17].利用四波混频的空间多模特性[18-19],可以将相互正交的轨道角动量模式引入产生多组并行的连续变量纠缠[20-22],利用轨道角动量模式匹配的参量放大器实现多通道量子隐形传态[23].四波混频因空间多模特性而成为高容量连续变量量子信息处理的重要资源.这些特点使得基于原子系综的四波混频过程取得一系列重要的研究进展,例如实现全光量子隐形传态[23]、可控的量子态延迟[24]、量子密集编码[25]以及量子克隆等[26].基于该系统的独特优势,本文理论上提出一种基于级联四波混频过程产生四模纠缠态的方案,通过非对称结构级联三个热铷原子池确定性地产生空间分离的四模纠缠态.然后,通过优化算法后处理从一组初始的正交振幅和正交相位压缩态重构出多模簇态,这种方法可以减小在有限压缩的条件下产生簇态而引入的额外噪声[27-29].该方法通过调控平衡零拍探测的本振光和信号光的相对相位和利用实数正交矩阵来重组优化结果以生成不同结构的簇态.
2 基于级联四波混频过程产生四模纠缠态
2.1 理论模型


图1 通过非对称结构级联三个四波混频过程产生四模纠缠态的示意图.,和是四波混频过程FWM1,FWM2和FWM3 的信号光;,和是真空输入模式;,,和是最终输出的四个模式;Pump1,Pump2和Pump3 表示三个四波混频过程的泵浦光;LO 表示用于平衡零拍探测(HD)的本振光场Fig.1.Schematic diagram of four-mode entangled states generated by cascading three four-wave mixing processes with asymmetric structure., and are seed beams of FWM1,FWM2 and FWM3,respectively., and are vacuum input modes.,, and are the final four output modes.Pump1,pump2 and pump3 denote the pump light of three fourwave mixing processes.LO denotes the local oscillator for balanced homodyne detection (HD).

2.2 四模量子纠缠特性
为了检验基于级联四波混频过程产生的四模态纠缠情况,利用部分转置正定判据来判断该体系产生的四模态是否纠缠[31,32].部分转置是反转正交相位算符的符号,即转置为,k是被转置的光束.因此,部分转置的协方差矩阵可以表示为:σ′T2NσT2N,其中T2N表示 2N维的对角矩阵,并且除了T2k,2k-1 以外的所有对角元素均为1.通过转置部分协方差矩阵把体系分成两部分,从而判断这两部分的纠缠情况.对于N模系统,需要验证 2N-1-1 种可能的两分情况,如果所有的两分情况均不可分,就可以证明产生了真正的N模纠缠态.这里协方差矩阵的表达式定义为σ〈ζζT〉,可以将四个模式的正交分量的对易关系写为,其中1和-1 分别表示对角元素为1和—1 的对角矩阵.对于高斯态的协方差矩阵必须满足不确定性关系:σ+iΩ≥0,这意味着σ≥0,即协方差矩阵的所有最小辛本征值应大于等于1.部分转置后的协方差矩阵最小辛本征值可以通过求解 iΩσ的本征值得到,当最小辛本征值小于1 时证明存在纠缠.对于四模态系统有两种两分情况需要分析,即4 种1×3和3 种2×2,共7 种情况.图3 展示了不同强度增益下7 个最小辛本征值的计算结果,结果表明7 种情况的最小辛本征值均小于1,并且随着强度增益的增加最小辛本征值逐渐减小,说明产生真正的四模纠缠态.

图2 当 G1=G2=G3=1.2 时四模态系统的协方差矩阵 (a)正交振幅的协方差矩阵 〈〉;(b)正交相位的协方差矩阵〈〉Fig.2.The covariance matrix of the four-mode state int he caseof G1=G2=G3=1.2 : (a)The covariance of amplitude quad-ratures 〈〉;(b)the covariance of phase quadratures 〈〉.
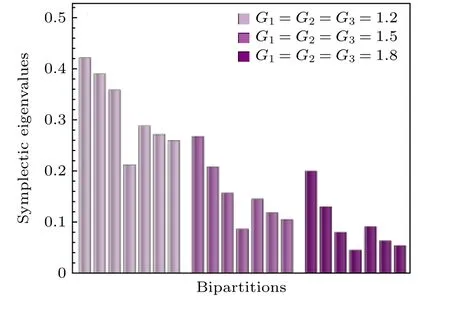
图3 不同强度增益情况下,四模态的最小辛本征值.不同颜色的条形图分别表示强度增益为1.2,1.5和1.8 时的最小辛本征值Fig.3.The smallest symplectic eigenvalues of four-mode state for different gains.Bar chart with different colors represent the smallest symplectic eigenvalues at gains of 1.2,1.5 and 1.8,respectively.
2.3 本征模
为进一步研究四模态系统内部的纠缠结构,还分析了系统中的本征模.多模高斯态经过Bloch Messiah 分解可以得到一组相互正交的单模压缩态和线性分束器网络[33].分解过程可表示为σXX其中Kdiag(η1,η2,···)是由本征分解协方差矩阵得到的特征值组成的对角矩阵,其值在对数空间代表单模压缩态的压缩度,U0是本征分解协方差矩阵得到的本征向量,其可以用线性分束器网络实现.这里我们分解协方差矩阵中与正交振幅相关的部分(分解协方差矩阵的正交相位部分和正交振幅部分结果相似),选择强度增益G为1.2,1.5和8,分别得到本征值和对应的本征向量如图4 所示.通过对本征模进行分析,发现经过级联四波混频过程产生的四模纠缠态可以等价为两个单模压缩态和两个真空态经过线性分束器网络得到.同时发现压缩值随着强度增益G的增加而变大,这意味着纠缠度增强.值得注意的是随着强度增益G的增加,压缩模和反压缩模中的和在四个模中占的相对权重变低,使得相应模式对整体的纠缠影响逐渐变小,这是由于系统的非对称结构导致的.

图4 对于不同强度增益 G,基于级联四波混频过程生成的四模纠缠态的本征模及其相应的压缩值.每幅图中的条形柱分别表示模,,和 的相对权重,图上面的数字代表压缩值.图(a)—(d),图(e)—(h)和图(i)—(l)分别对应强度增益 G 为1.2,1.5和8 时的本征模分解情况Fig.4.The supermodes of the four-mode entangled state generated based on the cascade four-wave mixing process and their corresponding squeezing levels for different gain values G.The bars represent the relative weight of the modes,,and,respectively.The number above the figure represents the squeezing levels.Figures (a)—(d),Figures (e)—(h)and Figures (i)—(l)correspond to the eigenmode decomposition when the gain values G are 1.2,1.5 and 8,respectively.
3 基于级联四波混频过程产生四模簇态
多模纠缠态作为量子信息技术的重要资源,不仅是基础量子理论领域[34],也是量子计算和量子信息处理应用领域的重要研究课题[35-41].簇态是具有很强的纠缠保持特性和丰富结构的多模纠缠态,作为量子计算的重要平台而得到广泛研究.第二节已经证明基于级联四波混频过程的输出态是四模纠缠态,本节通过操纵这些输出态生成连续变量簇态.
簇态的相互作用仅局限于相邻模式之间,各结点通过纠缠连接.在理想压缩的情况下,连续变量簇态定义为


根据簇态的定义,构造簇态的光学网络可以通过一个酉矩阵UV描述.文献[45]中已表明矩阵UV可分解为

其中XVRe[UV],为矩阵UV的实数部分;YVIm[UV],为矩阵UV的虚数部分.设此簇态在理想情况下对应的邻接矩阵为V,该簇态的正交分量满足(3)式,所以XV,YV和V之间满足如下关系:

在四波混频系统中可以从一组初始的正交相位压缩态经过后处理变换得到簇态.首先引入对角移相矩阵D,通过对输入态进行 π /2相移使正交振幅压缩变为正交相位压缩,从而使得所有输入模式均处于正交相位压缩态.在第二节将正交振幅的协方差矩阵进行本征模分解得到一个正交相位压缩态、两个真空态和一个正交振幅压缩态,因此移相矩阵的具体形式为Ddiag(1,1,1,I).在四波混频系统中酉矩阵UFWM可以表示为UFWMU0D,其中U0是第二节中本征分解协方差矩阵得到的本征向量[46].然后,根据文献[29],引入两个变换对输出的纠缠态优化后处理得到满足条件的簇态.总的变换结果U可表示为
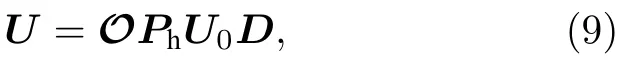
其中Phdiag(eiϕ1···eiϕN)是对本振光和信号光之间的相对相位进行相移的对角矩阵.实验上通过控制每个平衡零拍探测本振光和信号光的相对相位来实现.实数正交矩阵O可以通过调节噪声信号的增益或衰减来优化重构结果.此时得到的簇态的每个结点不是空间分离的单一模式,而是多模纠缠态的叠加[10].将变换的结果与给定的簇态转换矩阵UV作比较,可以找到一组参数满足如下关系:
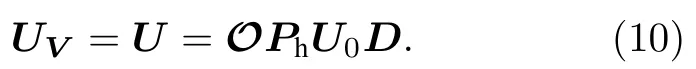
那么就实现了从四波混频系统生成的纠缠态经过平衡零拍探测的相位调控和输出信号的后处理到连续变量簇态网络的转变.这种变换存在一些特征,定义矩阵,其中是对角矩阵,并且是(10)式成立的充分必要条件.整理替换以上方程式可以得到:
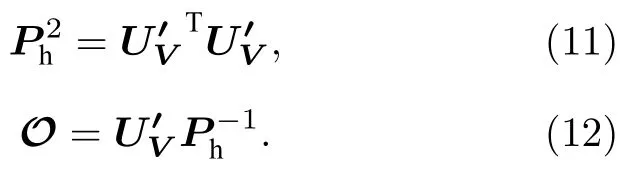
接下来将说明如何通过优化后处理,以邻接矩阵V给定的簇态UV为目标,将本文提出的基于级联四波混频系统生成的四模纠缠态优化重构,最终生成三种不同结构的四模簇态.实数正交矩阵O(θ)有N(N-1)/2 个自由度可以选择[46].特别地,对于四模态存在六个自由度.同时对角矩阵Ph有四个自由度.为了得到最优的正交矩阵O和对角矩阵Ph,用搜索算法寻找使矩阵O(θ)和Ph满足簇态条件的最小nullifiers值[41],该算法特别适用于高维参数搜索.当nullifiers 值均低于散粒噪声极限时,意味着四个输出态存在量子关联.然后根据van Loock和Furusawa[47]提出的连续变量多组份纠缠态的不可分判据,推导出满足连续变量四模线型簇态的条件为


其中,这些不等式的左侧和右侧分别是nullifiers方差的组合和边界条件.当左侧的所有方差组合都小于 4 时,说明重构出连续变量四模簇态.该方法可以减小在有限的压缩条件下生成簇态而引起的额外噪声.如果所有的输入模的压缩值不相等,则此方法可以以最佳的方式重新分配模式之间的相关性.
对于四模纠缠态存在三种簇态结构,即线型、T-型和方型簇态.首先研究线型结构的簇态.令三个级联四波混频的强度增益相等,即G1.2,进而可以得到实际的压缩值和反压缩值: {—6.7 db,0 db,0 db,6.7 db}.利用优化算法找到满足条件的正交矩阵O和Ph,实现线型簇态,结果如下:

经验证结果满足(8)式、(11)式和(12)式.Nullifiers的值分别为{1.174,1.87,1.783,1.386}.对于线型簇态,对应的散粒噪声极限为{2,3,3,2}.因此归一化后的Nullifiers 方差为{0.59,0.62,0.59,0.69},数值结果都小于1,说明低于散粒噪声极限.根据Nullifiers 的结果,可以计算出不等式(13)式—(15)式左侧方差的组合分别为: {3.04,3.63,3.15}.所有的组合结果都小于4,这意味着四模线型簇态可以由四波混频系统生成的纠缠态通过优化后处理得到.同时研究了不同强度增益时的Nullifiers 值,结果列在表1 中.对于强度增益较小时,不同的强度增益应用优化算法均找到最优值使得Nullifiers的归一化方差小于1,当强度增益为1.5和1.8 时,不等式(13)式—(15)式左侧方差的组合分别为{3.04,3.12,2.42}和{2.58,2.97,2.09},Nullifiers 的方差组合都小于4,满足van Loock-Furusawa 判据.
同样的方法也可以研究T-型和方型簇态的变换情况,满足连续变量四模T-型簇态的条件为

T-型簇态的散粒噪声极限为{2,4,2,2},归一化后的Nullifiers 方差如表2 所列.当强度增益为1.2,1.5和1.8 时,不等式(16)式—(18)式左侧方差的组合分别为{2.42,2.5,1.96},{1.76,1.84,1.6}和{1.52,1.52,1.44},Nullifiers 的方差组合都小于4,满足van Loock-Furusawa 判据.满足连续变量四模方型簇态的条件为

方型簇态的散粒噪声极限为{3,3,3,3},归一化后的Nullifiers 方差如表3 所列.当强度增益为1.2,1.5和1.8 时,不等式(19)式—(21)式左侧方差的组合分别为{2.7,2.7,2.1},{1.65,1.65,1.86}和{2.34,1.74,3.06},Nullifiers 的方差组合都小于4,满足van Loock-Furusawa 判据.结果表明当强度增益较小时,对于不同的强度增益,不同结构的簇态均可以找到相应的优化矩阵满足簇态条件.这意味着基于级联四波混频过程生成的四模纠缠态,可以通过调控输出光场的相位和后处理得到三种不同结构的簇态.但是对于强度增益较大时,应用此方法很难找到最优的变换矩阵使Nullifiers的归一化方差小于1,结果如表1、表2和表3 中的最后一行所示.这与非对称的级联四波混频系统输出端的模式结构有关,强度增益很大时和在四个输出模中占的相对权重逐渐变小并趋于0,和的相对权重逐渐变大并趋于1,这导致无法通过后处理转换为簇态.

表1 对于不同的强度增益,四模线型簇态Nullifier 的归一化方差Table 1.Normalized variances of the four-mode linear cluster state nullifiers for different intensity gains.

表2 对于不同的强度增益,四模T-型簇态Nullifier 的归一化方差Table 2.Normalized variances of the four-mode Ttype cluster state nullifiers for different intensity gains.
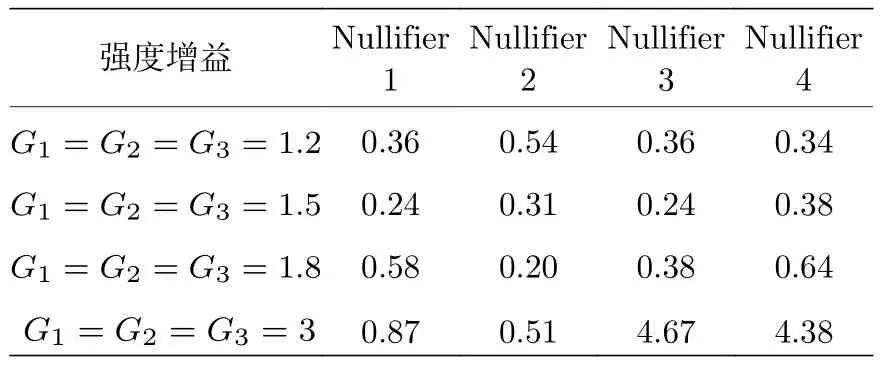
表3 对于不同的强度增益,四模方型簇态Nullifier 的归一化方差Table 3.Normalized variances of the four-mode square cluster state nullifiers for different intensity gains.
4 结论
本文提出基于级联四波混频系统产生四模纠缠态的方案,并调控输出态的相位和对噪声信号后处理重构出三种不同结构的簇态.首先利用部分转置正定判据证明该体系可以产生真正的四模纠缠态.然后分析四模纠缠态的本征模,发现该系统可分解为两个单模压缩态和两个真空态.最后研究了不同强度增益下基于优化算法重构簇态的情况,并利用van Loock-Furusawa 判据判断重构的态是否为簇态.结果表明在强度增益较小时,可以重构出线型、T-型和方型结构的四模簇态,强度增益很大时系统输出端的双模式结构影响生成四模簇态.这种基于级联四波混频过程重构不同结构簇态的多功能量子网络平台在量子计算和量子信息处理中存在潜在的应用.

