基于GM（1，1）模型和NAR神经网络的城市热水供热能力预测

刘双

（山东华宇工学院，山东 德州 253034）

0 引 言

近由于冬季时间较长，北方冬季温度低，因而，供暖是人们保持室内温度从而不影响正常生活的必要条件。而随着社会的进步、科技的发展以及国家环保政策的要求，人们的居住环境发生了巨大的改变，已由原来的平房小院变为了现在的住宅楼，因而，人们在冬天时的取暖方式也已由各家独自烧煤取暖改为了城市集中供暖，而居民住宅楼作为民用建筑，采用了城市热水供热的集中供暖系统。而为了满足城市居民的供暖需求，每个城市都被分为几个区域，由几家供热公司对所属区域的民用建筑进行供热，这就需要各供热公司的城市热水供热能力能够满足居民供暖的需求。为此，就需要对供热公司未来城市热水供热能力进行预测，针对此，本文通过查阅相关数据，获取了2001—2019年我国每年的城市热水供热能力数据，由于该样本数据为小样本数据，因而本文选用了灰色系统中的灰色预测模型对城市热水供热能力进行预测。灰色系统理论研究的是贫信息建模，它提供了在贫信息情况下解决系统问题的新途径。在灰色系统中，灰色预测是其很重要的一个部分，其优点在于对于“小样本，贫信息”的数据具有较好的预测效果，因而被广泛地应用于医学、工程技术、计算机等多个领域来预测各类数据。

本文运用灰色预测系统中的原始差分GM（1，1）模型（ODGM）对未来四年的城市热水供热能力进行预测，同时，为了验证灰色预测模型更适合用来预测小样本数据，本文还选取了NAR 神经网络预测模型对样本数据进行预测，通过对比两种模型模拟值的平均相对误差，最终得出未来四年的城市热水供热能力预测值。

1 我国城市热水供热能力现状分析

通过查阅国家统计局统计年鉴，本文得到了2001—2019年我国每年的城市热水供热能力数据，并绘制折线图，如图1所示。

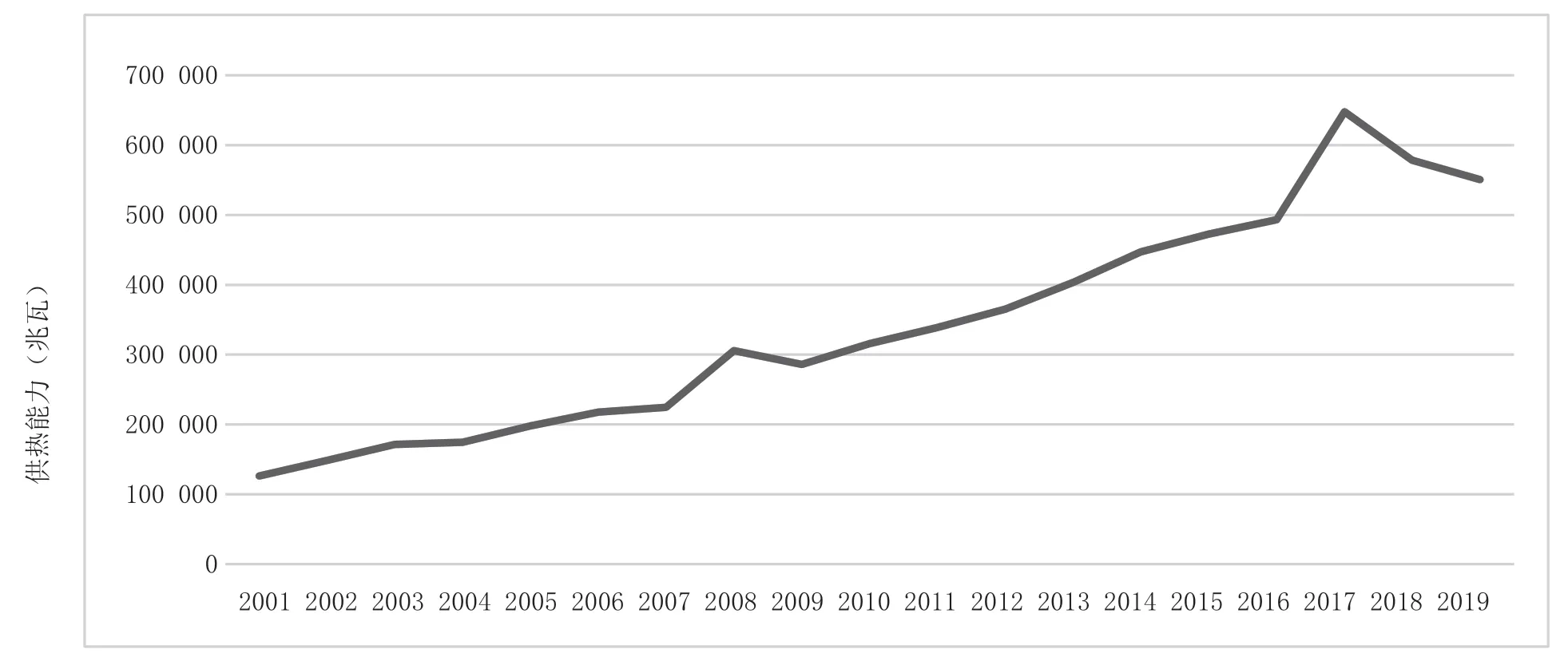
图1 2001—2019年城市热水供热能力

可以看出，从2001—2019年，城市热水供热能力虽然个别年份有所回落，但总体呈增长趋势，因而可以看成是接近齐次指数序列的非指数增长序列。2017年的城市热水供热能力达到最高值，为647 827 兆瓦，之后2018年、2019年有所回落，分别为578 244 兆瓦和550 530 兆瓦，较2017年分别回落了10.74%和15.02%，可见受各种外界因素的影响，我国每年的城市热水供热能力在保证总体增长的趋势下，也会有所不同，产生一定回落。

2 灰色预测模型原理及建模步骤

2.1 灰色预测模型原理

灰色预测是基于人们对系统演化不确定性特征的认识，运用序列算子对原始数据进行累加或累减生成，进而挖掘系统的演化规律，以此为基础建立灰色预测模型，从而对系统的未来状态做出定量预测。灰色预测模型包含均值GM（1，1）模型（EGM）、原始差分GM（1，1）模型（ODGM）、均值差分GM（1，1）模型（EDGM）和离散GM（1，1）模型（DGM）四种，本文选用了原始差分GM（1，1）模型（ODGM）对文中数据进行定量预测。

原始差分GM（1，1）模型（ODGM）是基于GM（1，1）模型的原始形式和运用最小二乘法估计出的原始形式中的模型参数，直接以原始差分方程的解作为1-AGO 序列的时间响应式所得到的模型。进而通过类减的方式，还原得到原始序列的时间响应式，该时间响应式就是所需的原始序列的预测模型，通过该预测模型，得出所要预测的数据。

2.2 灰色预测模型建模步骤[3]

第一步：设原始序列为：

=（(1)，(2)，…，(n)）

对其进行一次累加生成，得到的1-AGO 序列：

=（(1)，(2)，…，(n)）

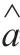
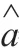
其中，分别为：

第二步：以（1）式的解作为时间响应式所得模型称为GM（1，1）模型的原始差分形式，求解得该时间响应式为：

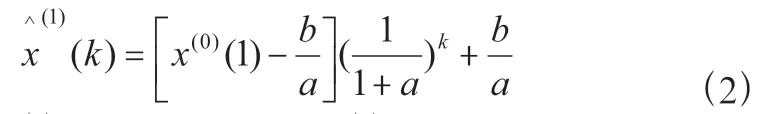
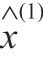
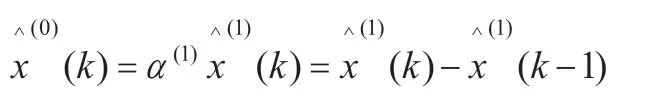
进而得出原始序列的预测模型为：

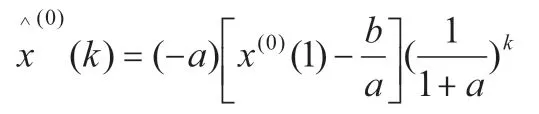
2.3 灰色预测模型精度检验[4]

为检验预测结果的准确性，还需对模型预测的精度进行检验，精度检验标准，如表1所示。

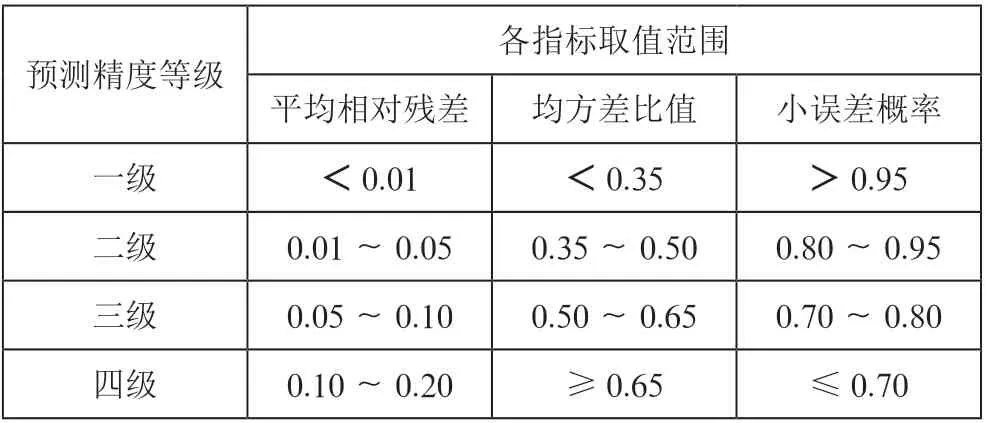
表1 精度检验等级参照表

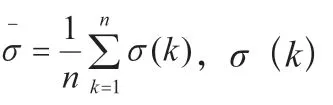
均方差比值为残差序列的均方差与原始序列的均方差之比。其中，和分别为：

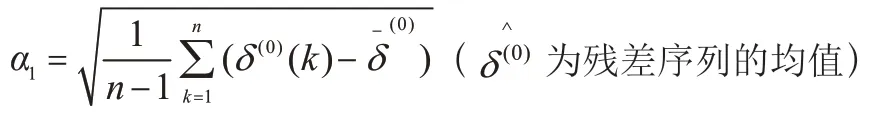
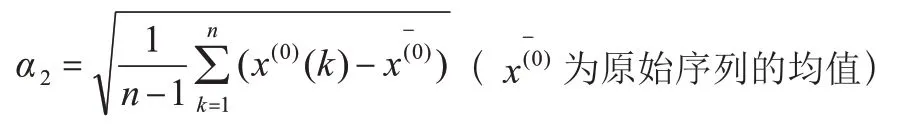
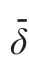
3 NAR 神经网络预测模型原理及步骤

3.1 NAR 神经网络预测模型原理

非线性自回归（Nonlinear Auto Regressive, NAR）神经网络模型是一种用于分析时间序列的动态神经网络模型，是由静态神经元与网络的输出反馈构成的回归神经网络。NAR动态神经网络本质上是静态神经网络结合输出反馈，由输入层、隐藏层、输入延迟层与输出层构成，是一个自回归过程，输出值取决于之前的值，而输入值为前一次的输出值。

3.2 NAR 神经网络预测模型步骤

NAR 神经网络的数学模型为：

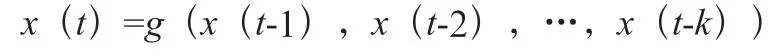
其中，为延时阶数，即时刻之前的数据期数，一般延时阶数的确定要根据所预测量的实际情况来确定；( )为NAR 神经网络所拟合出的非线性回归函数。

该模型是采用了递归预测方法，其特点为对1 步向前预测值进行循环使用，时刻的输出值由前期（-1），（-2），（-3），…，（-）的值所确定，而预测+1 时刻的输出值时，则由（），（-1），（-2），…，（-+1）的值所确定，以此循环，得出所需要的预测值，该方法由于不断地更换旧信息，代入新信息，因而预测精度相对更高一些。

NAR 神经网络的预测流程为：导入所需预测的样本数据—训练数据划分—确定延时阶数—确定各参数值—选择训练方法进行训练—残差检验—训练结束并保存网络—数据预测。

4 我国城市热水供热能力预测

4.1 灰色预测模型预测结果

本文以我国2001—2019年我国城市热水供热能力数据为原始序列，首先对该原始序列进行一次累加生成，得到的1-AGO 序列，和的数据如表1所示，然后建立原始差分GM（1，1）模型（ODGM），运用该模型对我国城市热水供热能力进行预测。

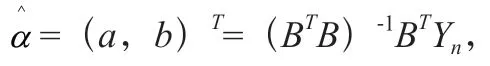
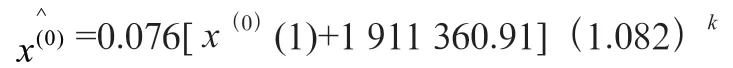
其中，的模拟值数据如表2所示。

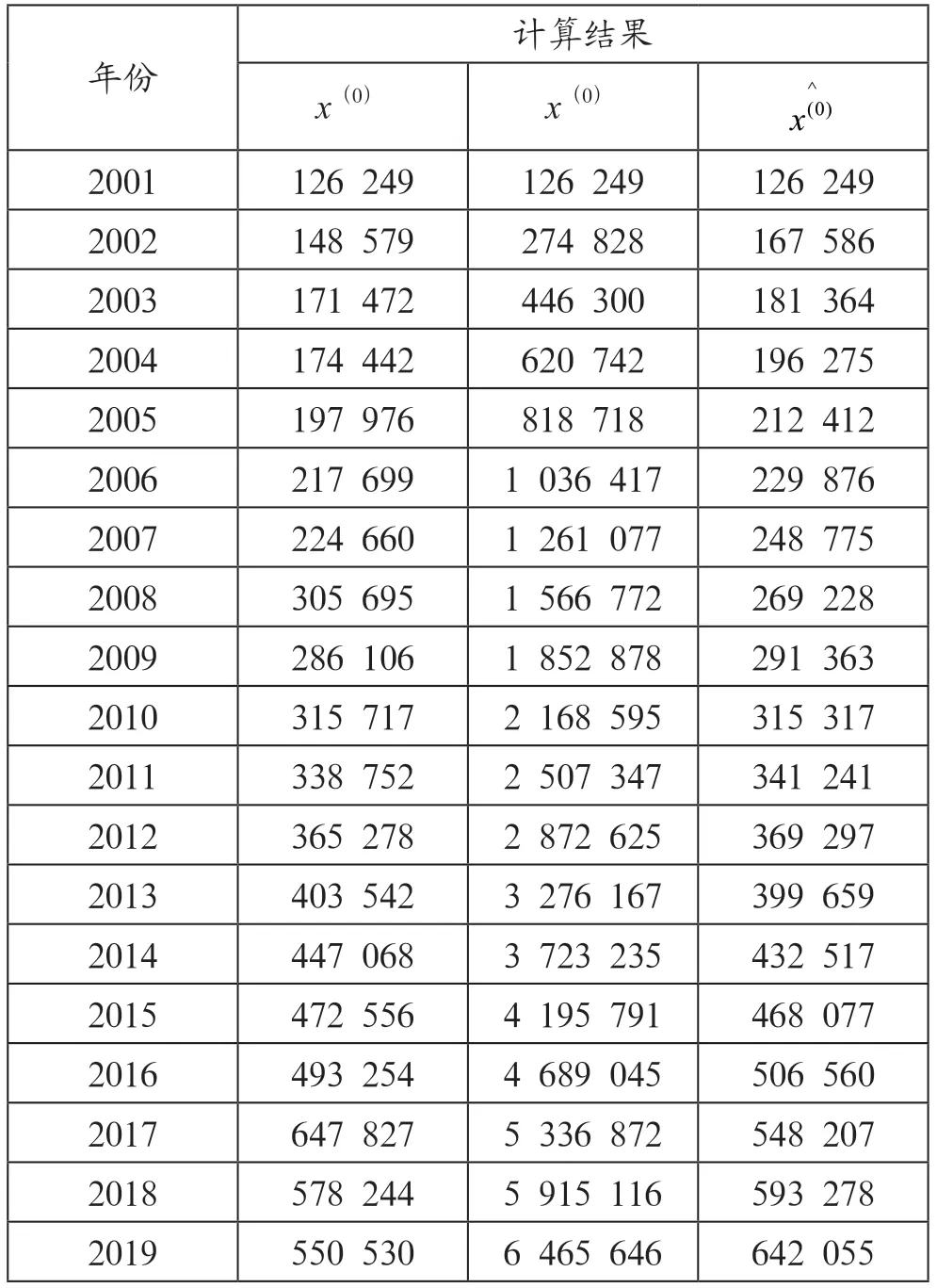
表2 实际值和模拟值计算结果

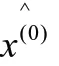
本文利用该预测模型预测得出了2020—2023年的城市热水供热能力预测值，结果如表3所示。

表3 我国热水供热能力预测值

4.2 NAR 神经网络模型预测结果

本文中2001—2019年我国城市热水供热能力数据为时间序列，设为（）={126 249，148 579，171 472，174 442，197 976，217 699，224 660，305 695，286 106，315 717，338 752，365 278，403 542，447 068，472 556，493 254，647 827，578 244，550 530}。

针对延时阶数的确定：若阶数过少，会造成历史数据的应用不完全；阶数过多，就会受到历史数据中畸形数据的干扰。因而为了避免产生上述影响，提高预测的精度，经过多次运行，最终延时阶数确定为3。

本文运用MATLBA 软件，选取前14 个数据作为训练集，后5 个数据作为测试集，对所建立的模型进行训练，经过多次训练后，最终确定了该样本数据的NAR 神经网络预测模型，并对未来四年的城市热水供热能力进行预测，结果如表4所示。

表4 我国热水供热能力预测值

根据原式序列与预测序列，计算得到平均相对残差为6.89%，该值大于运用灰色预测模型所得出的平均相对残差，说明运用灰色预测模型的稳定性和准确定都要好于NAR 神经网络预测模型，可见，灰色预测模型更适用于对“小样本，贫信息”的数据进行预测。

5 结 论

城市热水供热能力的大小影响着我国城市居民的日常生活，伴随着我国城市人口的不断增多，居民对生活质量的要求不断提升，越来越多的居民对于冬季室内供暖情况提出了更高的需求，因而，为了满足居民的需求，就必须制定相应的措施。具体措施如下：一是适当增加城市供热公司的数量以及相应的工作人员，保证在供暖日各居民住宅楼能够及时供暖，同时，如有居民家里存在暖气不热等问题时，能够有工作人员及时跟踪解决；二是完善居民住宅楼的供热系统，目前，仍有部分住宅小区，存在供热系统不完善或是年久失修等情况，导致在冬天来临时，不能做到及时供暖，为此，应在供暖日前，提前完善供热系统，对于存在问题需要维修的，应及时进行维修；三是政府部门应加大对于供热公司及各住宅小区供热系统的监管力度，切实保证居民的切身利益。

本文运用了灰色预测模型对我国城市热水供热能力进行预测，并通过与NAR 神经网络预测模型的预测结果进行对比发现，灰色预测模型更适合预测，预测精度更高，这是因为灰色预测模型更适合用来预测“小样本，贫信息”的数据，而本文中的数据恰好符合这一特点，因而通过本文可以得出，今后针对“小样本，贫信息”的数据，应尽量选用灰色预测模型进行预测。