基于神经网络的ZigBee通信抗干扰的研究
刘盛尧,高淑春,于海霞
(合肥职业技术学院 信息工程与传媒学院,安徽 合肥 230013)
0 引 言
ZigBee 网络是一个基于IEEE 802.15.4 规范的通信协议,用于家庭自动化、工业设备控制、医疗数据采集和其他低带宽需求的无线局域网。随着物联网设备以及网络的普及,设备在物联网中的部署不断增加,ZigBee 网络中出现了与其他网络之间的干扰问题。
目前很多研究在讨论增强ZigBee 的安全性,缓解干扰的解决方法,一般分为避免和共存两种。文献研究了ZigBee 网络在受到无线Wi-Fi 网络干扰时,单个网络中的节点通过信道分配来避免干扰。Kho等人提出了一种基于信道跳变的干扰避免方法,来提高 ZigBee 网络通信的包接受率。Huang等人利用Pareto 模型来预测Wi-Fi 信号的分组间隙,然后去动态的调整ZigBee 数据包的分组长度,在Wi-Fi 分组的间隙发送ZigBee 的分组,使两个不同网络数据包相互交替发送,达到共存。张招亮等提出了一种基于干扰强度和活跃比率干扰特征模型的信道分配机制,利用信道分配算法使得环境中所有无线网络通信质量最优,实现相互共存。但是以上方法多为单一的Wi-Fi 干扰研究,在强干扰时,抗干扰效果还有待改善,以往研究很多通过调整合适的距离,或者频偏来指导ZigBee 网络的部署,但这在宿舍,家庭等人们居住的生活场景下不太适用。
本文,为了在干扰信号的情况下解码ZigBee 信号,提出了一种基于学习的干扰抑制方法,该方法在物理层使用神经网络,此神经网络作为一个线性空间滤波器来抑制干扰,而不需要对干扰有任何了解。需要解决的是如何训练神经网络,使其能够实时解码数据包。为了解决这一问题,采用了一个小型的没有隐藏层的神经网络,并利用内在关系对其进行了优化。
1 问题描述
ZigBee 无线个域网络的构成,一般由一个ZigBee 网关服务于一个或多个ZigBee 设备,在这个网络中有一些其他的无线信号形成了干扰源,干扰了ZigBee 的无线通信,对这些干扰源有以下假设:
(1)ZigBee 的接收设备不知道干扰信号的带宽、波形和帧格式;
(2)干扰信号的带宽可以大于、等于或小于ZigBee 信号的带宽;
(3)干扰信号的波形可能会随时间变化。
对于这些干扰信号,其目标是确保ZigBee 设备的无线通信不受无线电干扰攻击,本文设计了一种神经网络过滤干扰信号,在存在未知干扰的情况下解码数据包,而不需要任何干扰知识。
2 基于神经网络学习的干扰缓解方法
2.1 ZigBee 物理层规范
ZigBee 是基于IEEE 802.15.4 标准的,工作在免许可的2.4 ~2.483 5 GHz(全球),902 ~928 MHz(北美和澳大利亚),868 ~868.6 MHz(欧洲)频段.我国使用2.4 GHz频段,段内分配了16 个信道,每个信道使用2 MHz 带宽每个信道间隔5 MHz。无线电使用直接序列扩频编码(DSSS)以及偏移正交相移键控调制(O-QPSK),如图1所示为2.4 GHz 调制和扩展功能。每4 个bit 流数据映射成一个符号,共2=16 种不同的符号,接着每个符号映射成32 个码片组成的一个PN 序列。PN 序列中的码片被看成是半正弦脉冲,并通过O-QPSK 整形后调制到载波上,并分别将下标为奇数的调制到Q 路正交支路上,将下标为偶数的调制到I 路同相支路上。

图1 2.4 GHz 调制和扩展功能图
2.2 信号传输公式化
如图2,按照信号处理流程,在传统的ZigBee 接收机物理框架中设计添加神经网络,在信号流经过频偏、相偏补偿后送入神经网络,缓解干扰信号,恢复ZigBee 信号。( 表示两个信号流,一个是干扰信号,一个是ZigBee 的有用信号, 表示ZigBee 的有用信号)

图2 ZigBee 接收机在面临干扰信号时解码ZigBee 数据包优化图
由于ZigBee 通常用于短程通信,因此,假设ZigBee 通信的无线电信号在视距和非视距下都是平坦信号。在此假设的基础上,将干扰缓解问题表述为一个数学问题。(n)∈C为图1中神经网络模块的两个输入信号流,其中为ZigBee 帧的样本数量。(n)∈C为ZigBee 信号,(n)∈C为干扰信号。那么,接收到的信号()可以表示为:

其中=[]是ZigBee 发射机与接收机之间的信道系数,=[]为干扰设备与ZigBee 接收机之间的信道系数,()为ZigBee 接收器的噪声。
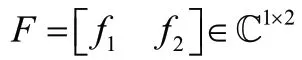
2.3 缓解干扰的神经网络优化
这时,采用一个小型的没有隐藏层的神经网络来替代滤波器,实时解码ZigBee 数据包,神经网络的输入向量为ZigBee 信号以及干扰信号(即()=[(),()])的实部和虚部,输出是ZigBee 有用信号流(即())的实 部和虚部,用R 和I 表示实部和虚部。
利用网络权重的内在关系,有:
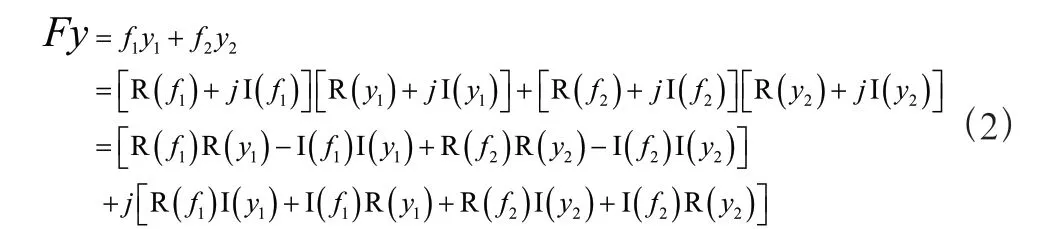
为了实现实时数据包检测,提出了一种加速训练过程的方法。根据(2)式,优化神经网络权重参数,定义=R(),=I(),=R(),=I(),故上式可以表示为:
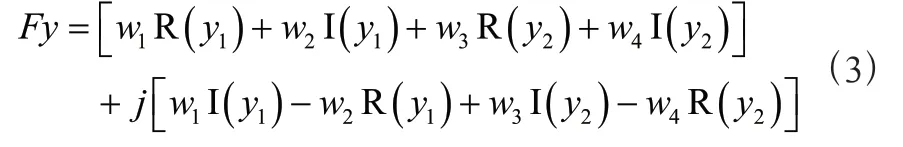
其中R()+I()+R()+I ()可映射为输出信号流实部 R(),I()-R()+I()-R()可映射为输出信号流虚部I()。此时仅有四个权重数,训练次数大大降低。用于缓解干扰信号的神经网络以及优化的神经网络如图3所示。
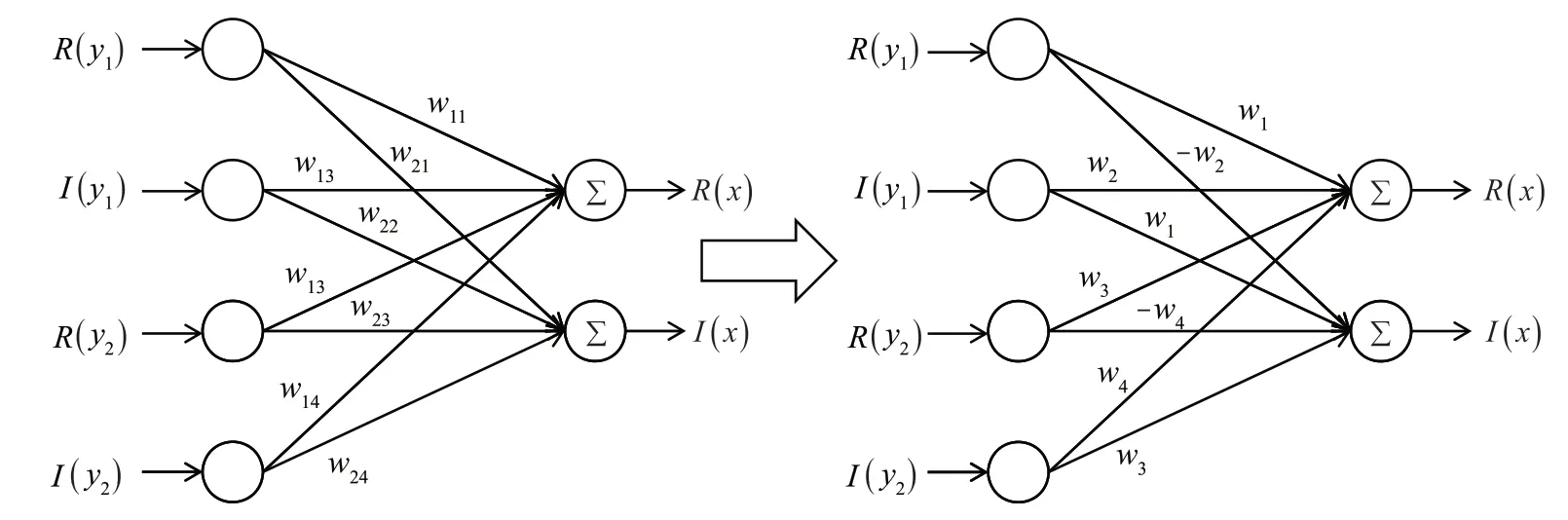
图3 缓解干扰信号的神经网络图
2.4 神经网络的权重训练
ZigBee 物理层帧结构中的前导域共4 个字节(32 bit)。对于这32 bit,每4 个bit 被调制成32 个码片组成的一个PN 序列。前导域中包含8 个Q/I 路的PN 序列,共256个码片。故选择一个总数256×4×2=2 048 个样本来更新神经网络的四个权重,根据(3)式,按图4的模型训练网络。其中256 是前导域码片数,4 为过采样率,2 为复数的分量数。如图所示,前1 024 个样本对应帧前导域中256 个码片的实部,后1 024 个样本对应帧前导域中256 个码片的虚部。
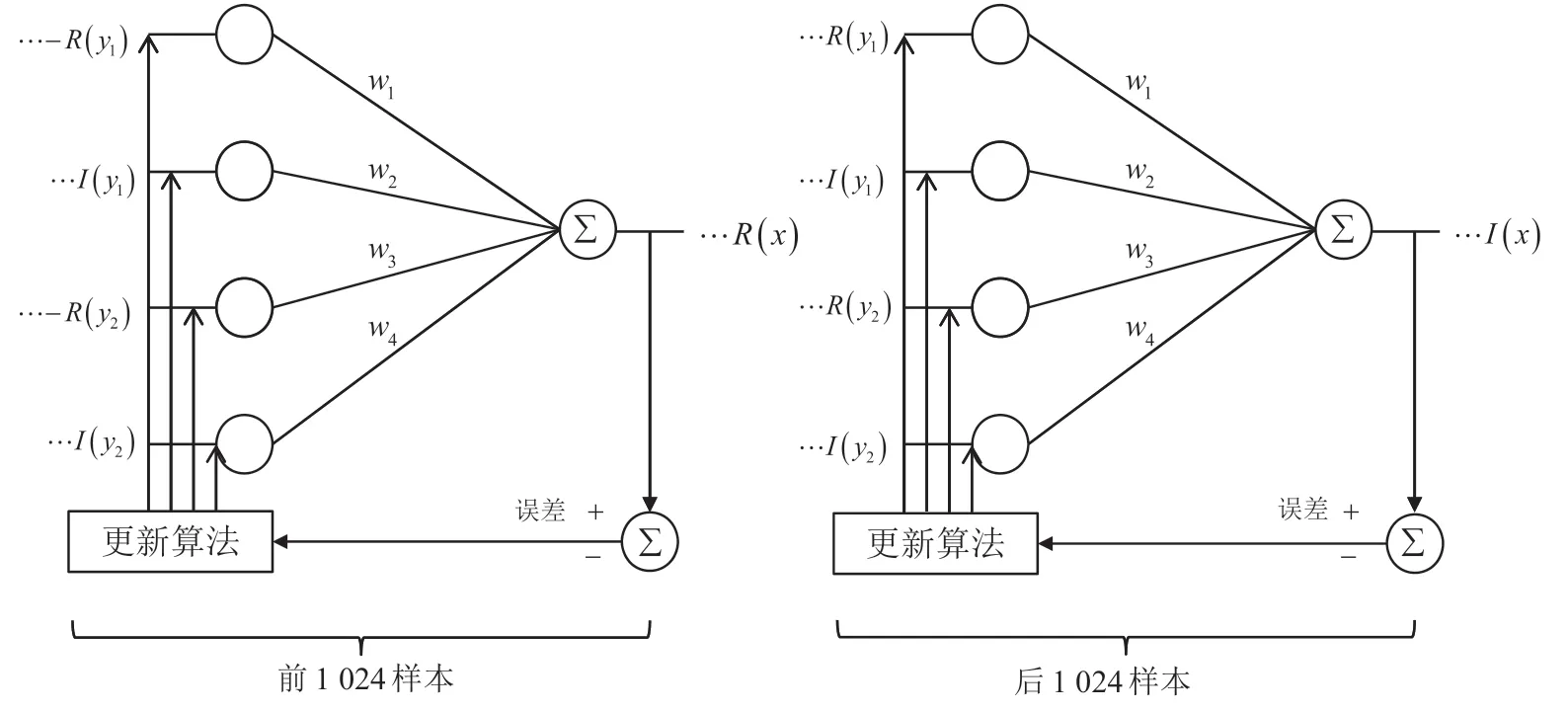
图4 神经网络的权重训练图
在该算法中,使用反向传播训练神经网络的权重,并将平方误差作为神经网络的代价函数。在训练过程中,使用自适应步长来更新权重。其中,对于图2中前1 024 个样本数据集,更新权重为:

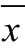
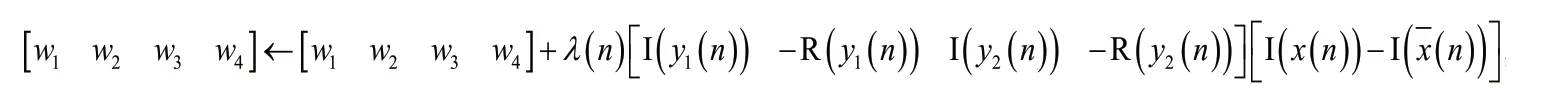

3 仿真结果与性能分析
3.1 ZigBee 接收器的性能指标
首先定义一些指标来评估ZigBee 接收器的性能.
干扰信号比ISR:针对ZigBee 接收机在干扰前后接收到的无线电信号,定义ISR 为:

其中,y()为关闭ZigBee 发射机,ZigBee 接收机接收到的干扰信号,y()为关闭干扰设备,ZigBee 接收机接收到的ZigBee 信号,N为被测信号采样数.
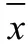

包接收率PRR:报文接收率是指解码成功的包占总发送包数的比例。
3.2 仿真分析
由于仅考虑ZigBee 的前导域,它是ZigBee 信号到达事件检测的关键问题。其他信号干扰前导域即会导致ZigBee样本存在较大失真。发射的ZigBee 信号的Q/I 路采样流都由多个正、负半正弦脉冲组成,故通过MATLAB 仿真ZigBee 半正弦脉冲信号模型和ISR 值不同的干扰信号,ISR 从-10 dB 到20 dB,对 MSE 以及PRR 进行相关分析。
图5为本文提出的神经网络对不同ISR 值的解码MSE.可以看出,当ISR 为20 dB 时,MSE 小于3.5%。这意味着即使干扰信号比ZigBee 信号强20 dB,所提出的基于神经网络学习的方法也可以在零噪声情况下解码ZigBee 数据包。表1为使用本文算法以及未使用本文算法传统接收机对不同ISR 值时的平均包接受率PRR,可以看到,提出的ZigBee 接收器达到了平均98%的PRR,而传统接收器的平均PRR 仅为49.34%,且在ISR 即干扰信号越大,对包接受率影响越大。
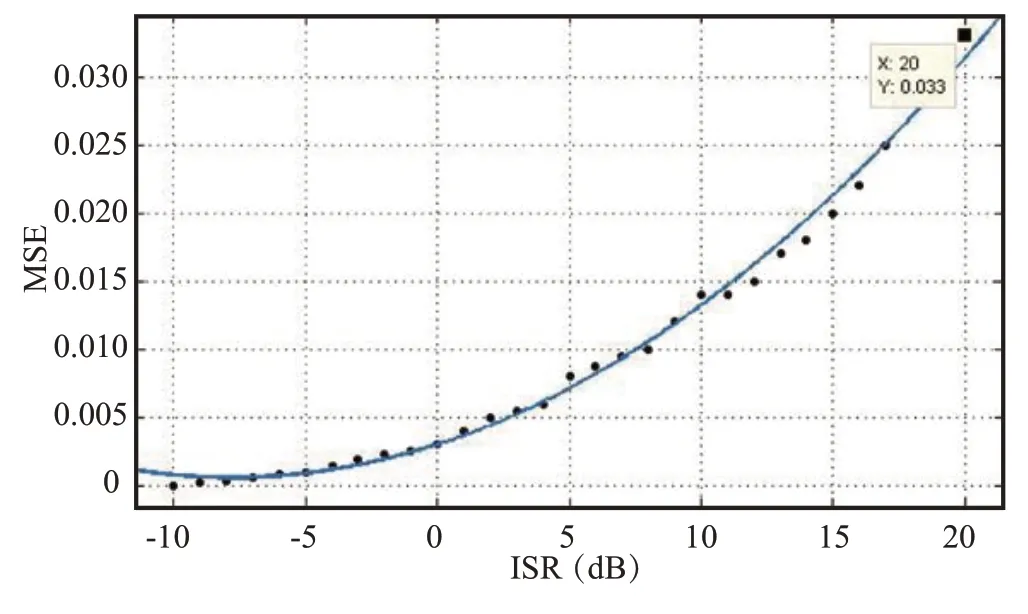
图5 不同ISR 下的MSE 图示

表1 包接受率随JSR 值不同的变化
4 结 论
在本文中,提出了一种无隐藏层的神经网络解码有干扰信号的ZigBee 数据包,并用ZigBee 包的帧前导域进行训练。仿真结果表明,在干扰信号下可以解码ZigBee 信号,整个传输过程没有出现丢包现象,而且采集到的数据值准确,表明系统具有较好的可靠性和稳定性,对今后ZigBee 接收机的设计有一定的理论意义。

