基于Smoothieware的双臂SCARA型3D打印机设计

毕忠梁，单家正，赵夫超

(安庆职业技术学院 机电工程学院，安徽 安庆 246003)

0 引言

以增材制造为背景的3D打印技术目前已经广泛运用在智能制造行业中，3D 打印机种类很多，主要分为桌面级和工业级两大类。其中桌面级3D打印机主要以笛卡尔坐标系XYZ机型为主，控制部分大多采用源代码开放的Marlin固件。而采用双臂结构的3D打印机还是较为少见[1]。

0.1 研究目的

桌面级3D打印机如果采用XYZ结构则一般体积较大，结构呆板，不便于移动和携带。机械臂型3D打印机具有体积小以及移动速度快等优点，但是一般SCARA型机械臂为单臂结构，末端承载能力不强，不便于安装3D打印喷嘴。本文设计一种双臂结构打印机，增加末端刚性，提高打印精度，同时双臂可折叠，便于设备携带，此改进不失为一种创新。

0.2 研究内容

由于双臂SCARA运动轨迹规划算法比较复杂，目前市面上3D打印机固件多为AVR开发，其运算能力无法满足要求。本设计采用Smoothieware固件控制，32位ARM处理器，将双臂SCARA型机械臂运动轨迹算法融入固件中，使其能够满足打印需求[2]。

1 双臂SCARA机械臂结构

双臂SCARA型机械结构不同于单臂SCARA，单臂SCARA的大臂和小臂分别由一个电机驱动，两个臂分别绕大臂的两个端点旋转运动。双臂SCARA机械臂两个电机分别驱动左右两组大臂，而小臂在末端铰链，实现机械臂的末端执行器在XY二维平面内定位，双臂SCARA比单臂SCARA的刚性更好，控制精度更高。

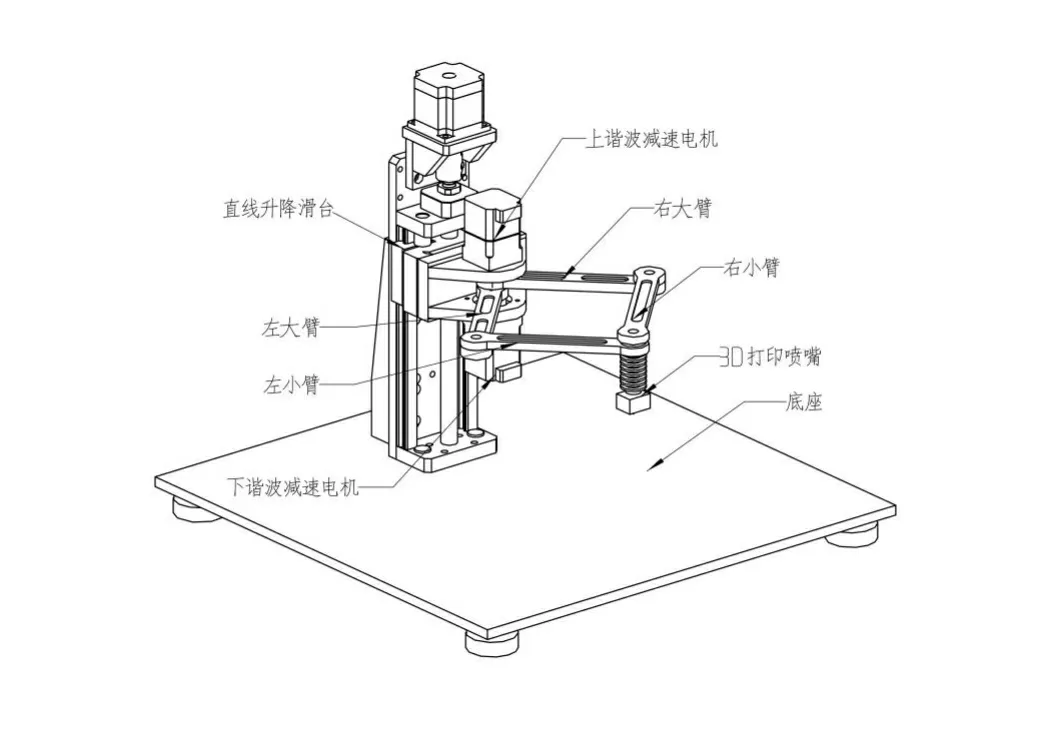
图1 双臂SCARA型机械臂结构示意图

如图1所示，双臂SCARA型机械臂在水平面上只有两个自由度，采用四杆等臂长结构关节臂。其主要机构由底座，左大臂、左小臂、右大臂、右小臂，直线升降滑台，3D打印喷头等部分组成。底座固定支撑整个机构，底座的下方安装打印热床。直线升降滑台竖直安装，可带动整个机械臂沿着Z方向做升降的直线运动。左右两组关节臂分别由上下两个精密谐波减速电机驱动，左右两组机械臂均绕同一个枢轴做旋转运动，两组关节臂在末端铰连合成运动[3]。不用的时候打印臂可以折叠向后收起，减少空间占用。

2 双臂SCARA型机构运动学分析

要研究双臂SCARA的控制系统，并修改Smoothieware固件轨迹规划算法，就必须先建立双臂SCARA的运动学模型，求出运动学正解和逆解。运动学正解是将各个关节之间角度转化为末端的笛卡尔直角坐标系的坐标值，运动学逆解是已知末端的笛卡尔直角坐标系的坐标值，求解各个关节的角度，从而驱动电机旋转。单臂SCARA的机械臂是由两个连杆通过旋转的关节串联而成，大臂与小臂的夹角决定了末端的位置，双臂SCARA不同的是由两组4个等臂连杆并联组成，两组大臂的夹角决定末端位置，情况比单臂SCARA要复杂很多。

2.1 双臂SCARA运动学正解

双臂SCARA的运动学正解是在已知所有连杆臂长和驱动电机关节角度的情况下，计算出机械臂末端的位置和姿态。双臂SCARA的平面运动如图2所示，在平面直角坐标系XOY下，两组机械臂四杆采用等臂长连杆，左右两组机械臂OB和OD均绕O点旋转，由上下两个谐波减速电机驱动，将O点设置为坐标系原点。左大臂、左小臂、右大臂和右小臂设计为等臂长结构，长度均为L，左大臂OB由上谐波电机驱动，与基础坐标系夹角为α2，右大臂OD由下谐波电机驱动，与基础坐标系的夹角为α1。左小臂和右小臂在A点铰链，A点即为末端执行器位置，其在平面坐标系中坐标设置为(Xa，Ya)。

通过简单的平面几何计算得到，末端A的X坐标为向量OB与向量AB在X轴上投影之和，末端A的Y坐标为向量OB与向量AB在Y轴上投影之和[4]，所以末端A点在平面坐标系中的位置坐标表达式为：

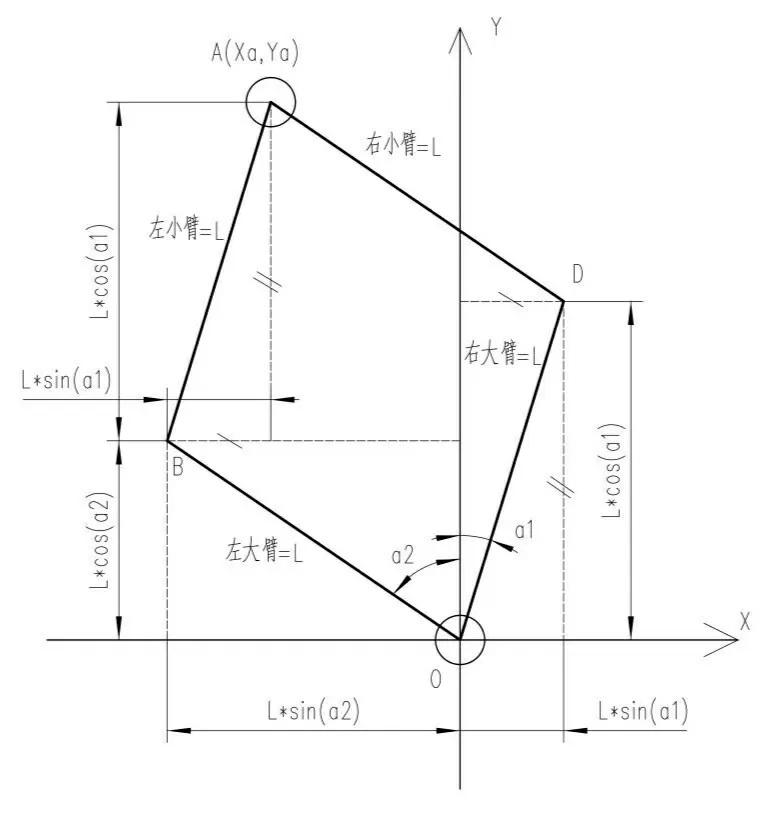
图2 运动学正解示意图

2.2 双臂SCARA运动学逆解

双臂SCARA的运动学逆解是在已知机械臂末端A点在平面坐标系中的位置坐标(Xa，Ya)和四杆等臂长L，计算出左大臂OB和右大臂OD的关节角度α1、α2。由于双臂SCARA的运动学逆解不是唯一的，因此求解比正解要复杂。如图3所示，同样是等臂长四杆结构臂长为L，连接OA过A点做OC垂直OB相交与C点。对于三角形ΔOBA，由余弦定理可得：

设k1=cosβ2，式(1)可写成：

设k2=sinβ2，由式⑵可得，k2有两个解：

当K2为正值时，机械臂处于一二象限，打印区间为机器正面区域；当K2为负值时，机械臂处于三四象限，运动方向为机器背面区域，由于机器设计时打印区间均在机器正面，所以K2始终为正。当K2=0时，机械臂处于奇异点，即末端位置在机械臂伸长最远端和机械臂收缩的最近端，当处于奇异点时β1=kπ(K∈Z)[5]。由于大臂小臂设计时无法重叠，因此K2不能为0，综上K2∈(0,1]。

由式⑵和⑶可得：

对于ΔOAE，可得：

对于ΔOAC，设|OA|=R，则：

由式(6)和(7)可得：

至此分别求出左大臂OB和右大臂OD的关节角度α1、α2：

在这里，无论是求解α1还是α2，均采用双变量反正切函数atan2计算，而没有采用反正/余弦函数asin/acos，这是因为atan2(Y，X)的值域为[-π，π]，双臂SCARA机械臂无论是左大臂OB还是右大臂OD，其关节角的取值范围也都在此之间，因此采用atan2(Y，X)更加的直观和方便，也避免了额外的角度范围判断。另一方面atan2(Y，X)相对于asin(X)或者acos(X)而言，计算精度也更高。因为实际机器人的臂长、零点、减速比等运动学参数有误差，asin(X)或者acos(X)会使误差放大，逆解精度均匀性比atan2(Y，X)差，综上所述在求解机器人运动学逆解时采用atan2(Y，X)来计算[6]。

3 基于Smoothieware系统软件设计

目前市面上的桌面级3D打印机大多采用的是基于AVR开发的Marlin固件，双臂SCARA机型不同于普通笛卡尔坐标系结构，其运动轨迹算法计算复杂，而且采用谐波减速电机驱动，为满足定位精度，电机步距角选择很小，脉冲的细分倍数较高，对处理器性能要求比较高，使用Marlin固件存在卡顿现象[7]。因此为了满足使用的要求，本设计采用Smoothieware固件。Smoothieware是一款面向LPC17xx微控制器(ARM Cortex M3体系结构)的基于C++编写的开源固件，可以在mBed、LPCXpresso、SmoothieBoard、R2C2或任何其他基于LPC17xx的控制卡上运行。采用的是32位Cortex M3主控芯片，100MHZ的主频，运算能力很强，完全可以满足双臂SCARA机型的性能要求。Smoothieware固件已经集成了单臂SCARA的算法，要使其能控制双臂SCARA需要编写其运动控制部分算法，其运动学逆解部分程序代码如下：

void dual_armSCARASolution::cartesian_to_actuator( float cartesian_mm[], float actuator_mm[] ) ∥笛卡尔坐标转换为关节坐标

{

float SCARA[X_AXIS],SCARA[Y_AXIS]；∥末端喷头的平面坐标系坐标值

SCARA_COS；∥cosβ2值

SCARA_SIN；∥cosβ2值

SCARA_T1；∥|OC|值

SCARA_T2；∥|AC|值

SCARA_a2；∥左关节OB与基础坐标系夹角为α2

SCARA_a1；∥右关节OD与基础坐标系夹角为α1

SCARA_COS=(SQ(SCARA[X_AXIS])+SQ(SCARA[Y_AXIS])-2.0f*SQ(this->arm_length)) / (2.0f * SQ(this->arm_length));∥arm_length为配置文件中设置机械臂的臂长

if (SCARA_COS > 0.99f)

SCARA_COS = 0.99f；∥避开机械臂处于奇异点的位置

else if (SCARA_COS <-0.99f)

SCARA_COS = -0.99f；∥避开机械臂处于奇异点的位置

SCARA_SIN = sqrtf(1.0f-SQ(SCARA_COS ));

SCARA_T1 = this->arm_length+this->arm_length*SCARA_COS;

SCARA_T2 = this->arm_length*SCARA_SIN；

SCARA_a2 = (atan2f(SCARA_T1, SCARA_T2)+atan2f(SCARA[X_AXIS],SCARA[Y_AXIS]));

SCARA_a1= (atan2f(SCARA_T1,SCARA_T2))-(atan2f(SCARA[X_AXIS],SCARA[Y_AXIS]);

actuator_mm[ALPHA_STEPPER] = to_degrees(SCARA_a2)；∥将α2弧度换算为上电机角度

actuator_mm[BETA_STEPPER ] = to_degrees(SCARA_a1)； ∥将α1弧度换算为下电机角度

}

将修改好的固件重新刷入控制卡，经过调试系统运行正常，测试打印精度较高。

4 结论

本文设计并试制出的这种具有双臂机构的SCARA3D打印机，相比于传统的桌面级3D打印机具有体积小、刚性好以及移动速度快等优点。但是此结构3D打印机也存在一些不足，主要是连杆的加工装配精度对机械臂运行轨迹的影响较大，同时原点的初始角度值也会影响打印精度，后期还需要进一步优化。