基于ANSYS的某电站压力钢管失稳破坏原因分析
涂从刚,孔垂雨,杜蔚琼
(水利部水工金属结构质量检验测试中心,河南 郑州 450044)
1 项目概况
四川凉山彝族自治州境内某电站,从山顶的前池引水,除部分管段为埋管外,其余压力钢管为沿山体布置的明管段,钢管两端由镇墩固定,下方由多个支墩支撑。钢管伸缩节采用复式波纹补偿器来进行轴向和径向位移补偿,补偿器两端的波纹管为8层06Cr19Ni10不锈钢板压制而成,单层板厚1.5mm,总厚度12mm,设计内压10.6MPa,波纹补偿器的短套筒、连接套筒为WDB620高强钢,导流筒、加强铠等其余部件为Q235B。
根据电站试验记录,压力钢管共进行两次静载水压试验,第一次静载水压试验时8#波纹补偿器损坏并导致7#镇墩至8#镇墩间压力钢管全部脱墩,管理方在未确定故障原因的情况下,对8#波纹补偿器进行更换处理;3个月后进行第二次静载水压试验,在充水过程中,10#波纹管开始缓慢变形,连接的钢管也随之上翘,降低水压后变形消失,施工人员用钢缆约束变形位置的钢管后继续缓慢增加水压,直至达到设计水压钢管未出现异常,随后进行24h静置试验。静置试验结束后8#波纹补偿器和10#波纹补偿器均出现不同程度破坏。根据现场勘察,两组波纹补偿器的失稳特征基本相同,均出现单侧膨胀,中间连接套筒整体偏离轴线,整个波纹补偿器变形呈现“Z”状,因支墩缺少对压力钢管的径向的约束,变形的波纹补偿器将连接的钢管局部抬起或水平偏移导致脱离支墩。
事故造成该电站不能按期交付,对业主、施工单位等均造成了不同程度的损失,也加剧了电站所在地电力供应紧张的局面。
本文以损坏的8#波纹补偿器为研究对象分析钢管失稳原因。为业主及施工单位后续整改处理提供依据,也为同类型电站的压力钢管安装施工提供借鉴。
2 波纹补偿器取样分析
波纹补偿器是利用波纹管弹性元件的有效伸缩变形来吸收管道变形的一种补偿装置。近年来,一些新设计施工的引水式水电站的压力钢管均采用波纹补偿器进行钢管的轴向、径向与小角度位移的补偿。
根据第一次静载水压试验破坏的8#波纹补偿器波纹管切割取样结果,该波纹管不锈钢板共有5层,单层厚度1.4mm,实际总厚度7mm,与设计图纸规定的12mm不符。从取样结果分析波纹管厚度不足会导致其刚度降低,可能诱发失稳破坏。
3 基于ANSYS失稳原因分析
3.1 有限元模型的建立
波纹补偿器的前后连接套筒、短套筒、波纹管及加强铠为主要受力构件,使用四节点壳单元SHELL181构建有限单元模型。波纹补偿器在静水压工况下,前后短套筒与压力钢管连接,因而承受钢管的轴向力和弯矩。为方便计算轴力和弯矩,将整段钢管含波纹补偿器简化成梁单元模型,根据压力钢管设计图纸,8#波纹补偿器上游端距镇墩5.839m,下游端距镇墩114.385m,波纹补偿器自身长度2m,支墩间距10m,依照图纸尺寸分别建立2段钢管的梁单元模型,梁单元取Beam189,单元截面取钢管实际内外径尺寸。8#波纹补偿器波纹管壁厚度12mm,波纹管所用06Cr19Ni10不锈钢材料属性采用如下值:弹性模量193000MPa,泊松比0.31,密度7750kg/m3;连接套筒、短套筒所用WDB620高强钢材料属性采用如下值:弹性模量206000MPa,泊松比0.30,密度7850kg/m3。
3.2 载荷及约束边界条件设定
波纹补偿器在静水压工况下,其承受的载荷包括温度变化引起的载荷、管内水压力、管内水自重、结构自重以及轴力与弯矩。其中温度载荷参照电站所在地11月份温差变化较大的11月14日(7~21℃)作为温度载荷。钢管内水重根据两段钢管的长度和管径来确定;在设定重力加速度9.806m/s2后,波纹补偿器和钢管的结构自重通过ANSYS Workbench自动计算并施加;波纹补偿器两端的轴力与弯矩使用梁单元有限元模型计算而得到,经计算,作用在8#波纹补偿器两端的轴力为5.47×105N,上游端弯矩为20389N·m,下游端弯矩为33331N·m。波纹补偿器内压均设置为1.0MPa,以便于临界载荷计算。波纹补偿器的约束边界条件的参考坐标系采用柱坐标系,补偿器上游侧短接管端部约束其径向、环向及轴向,下游侧短接管端部约束其环向,释放径向及轴向自由度。
3.3 线性屈曲分析
线性屈曲分析除了得到结构的临界载荷特征值外,也提供了结构模型在临界载荷下的屈曲失稳模态。波纹补偿器静力学计算完成后,直接用静力学分析与特征值屈曲分析耦合的方式进行线性屈曲计算,计算完成后提取其前6阶的特征值与模态。特征值屈曲分析第1、2阶的特征值和屈曲模态相对其他阶更能准确的反映结构的失稳形式,因此重点研究结构的第1、2阶屈曲模态,第1、2阶屈曲模态如图1—2所示。
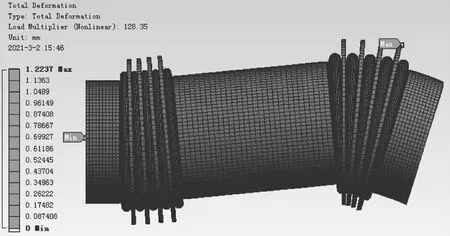
图1 波纹补偿器的1阶线性屈曲模态

图2 波纹补偿器的2阶线性屈曲模态
从提取的第1、2阶特征值和屈曲模态来看,波纹补偿器在达到临界载荷下的1阶屈曲失稳形态同现场实际情况完全一致,下游端的波纹管12点钟方向局部膨胀导致补偿器整体呈“Z”字形扭曲,第2阶屈曲模态为下游端的波纹管9点钟方向局部膨胀。结构屈曲模态变形的最大值通常在结构薄弱部位出现,根据1阶和2阶屈曲模态的特征,初步认为该波纹补偿器波纹管的径向结构刚度偏弱,第1阶的屈曲模态即出现波纹管径向弯曲导致波纹补偿器“Z”字形扭曲。第1阶屈曲的特征值λ=128.4,结构出现屈曲失稳的临界载荷为128.4MPa。该载荷明显偏高,可将其作为非线性屈曲内压的上限。
3.4 非线性屈曲分析
非线性屈曲分析是一种基于线性屈曲分析模态的非线性静力学分析,该分析过程一直持续到结构出现失稳的临界载荷为止[3]。结构非线性屈曲分析包括特征值屈曲和非线性静力分析两个步骤。特征值屈曲用于预测一个理想结构的理论屈曲强度(临界载荷),即计算造成结构负刚度的应力刚度矩阵的比例因子λ(特征值),给定载荷的λ倍就是临界载荷。特征值屈曲可初步预测临界载荷的上限,其屈曲失稳模型可作为非线性计算的基础[4]。非线性分析是对屈曲失稳模型进行的非线性静力分析,ANSYS中采用Newton-Rolfson迭代算法进行非线性计算,并判断迭代残差是否收敛,若收敛则继续计算直到迭代次数满足要求时结束,若不收敛则当迭代残差大于ANSYS阈值时终止计算,其迭代过程中考虑了材料的非线性弹塑变形特性及结构变形,在结构塑性变形阶段计算更为准确[5]。
3.4.1材料的非线性特性
波纹补偿器的波纹管出现局部塑性变形,因此非线性计算须考虑材料的非线性特性(线弹性本构关系)。ANSYS Workbench中通常采用双线性随动强化模型(BISO)来描述塑性材料在弹塑性阶段的本构关系,即在指定正切模量(Tangent Modulus)后,用双线性曲线分别描述材料在线弹性和塑性区间的应力与应变关系曲线。波纹管不锈钢的线弹性本构关系采用ANSYS Workbench自带的不锈钢BISO曲线,如图3所示。

图3 波纹管不锈钢的材料线弹性本构关系曲线图
3.4.2含初始缺陷的模型及缺陷比例因子
结构的失稳是逐渐累积的过程,在接近临界载荷时,结构局部开始出现微小的变形缺陷,在达到临界载荷时,缺陷逐渐变大,结构承载能力变弱直至突然失稳或溃塌。ANSYS中建立的初始有限元计算模型是没有缺陷的理想几何体,因此需要人为给模型施加一个初始缺陷,才能有效发生屈曲失稳,最直接的方式为参考特征值屈曲分析的模态形式,通常提取第1阶屈曲模态的模型作为含初始缺陷的模型[6],非线性屈曲分析对含初始缺陷的结构模型以逐渐增加载荷的方式进行非线性迭代计算,直到结构在某一载荷处突然出现明显的大变形(即局部失稳),非线性迭代无法收敛为止。在调用含初始缺陷的模型时需指定缺陷比例因子,即屈曲模态模型在失稳状态下变形部位位移量的放大倍数。缺陷比例因子根据模型大小而定,因为波纹补偿器总长2000mm尺寸较小,缺陷比例因子设为2.0较合理。
3.4.3含初始缺陷模型的非线性计算
非线性屈曲分析的核心是基于载荷累积方式的对含初始缺陷模型非线性迭代计算,设置数量合理的载荷步(Load Step)能细化载荷累积的步长,可更为精确的计算出模型出现失稳时的临界载荷[5]。该波纹补偿器壳单元模型单元数较少,载荷步设置为初始值210,最小200,最大240,系统根据计算量动态调整。内压载荷设置为18.0MPa,其余边界条件同线性屈曲相同,计算开始后至非线性迭代发散,并在迭代发散前收敛的最后一个载荷步时计算终止。提取最后一个载荷步下的模型最大位移,建立载荷增长同结构最大位移的对应关系曲线图。模型非线性屈曲失稳形态如图4所示,内压-位移变化曲线如图5所示,原设计波纹补偿器内压-位移变化计算结果见表1。

图4 原设计波纹补偿器非线性屈曲失稳形态

图5 原设计波纹补偿器内压-位移变化曲线
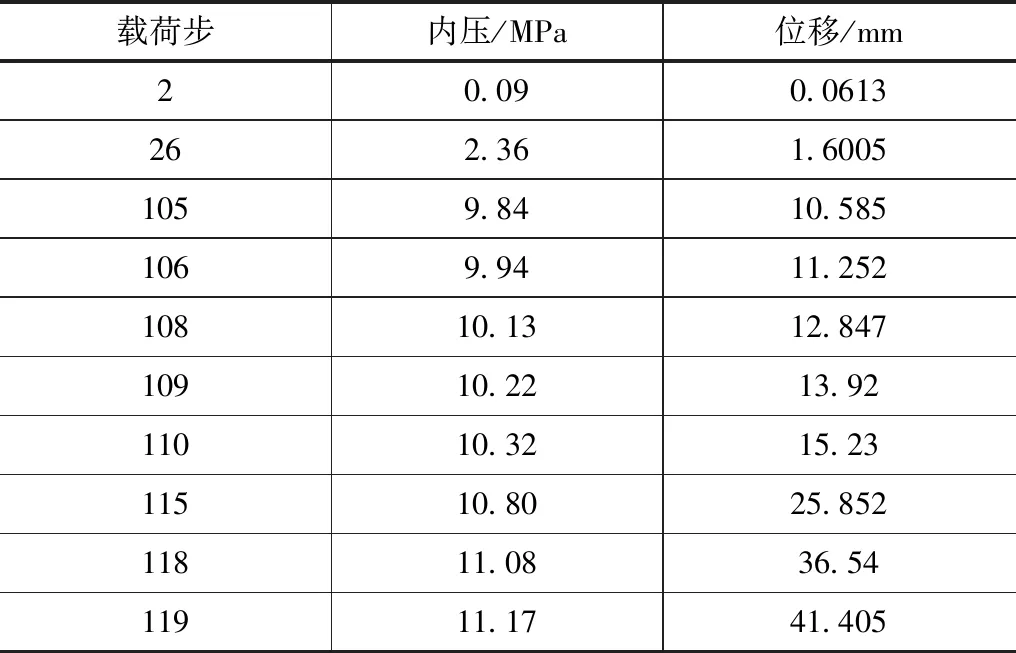
表1 原设计波纹补偿器内压-位移变化计算结果数据表
根据图5所示,内压力从0MPa开始逐渐增加时,波纹补偿器结构的位移随着载荷增加,在内压0~8.0MPa之间位移呈线性变化,结合表1的数据,内压力达到9.94MPa后,位移增长幅度随着载荷的线性增加逐渐变大,当内压达到10.32MPa时,位移增长幅度突然加快,结构开始失稳,内压在11.17MPa左右时非线性迭代结束,位移达到最大值。通过图4可见其屈曲失稳形态同现场实际情况完全相同,出现失稳的临界载荷为10.32MPa,小于其设计内压力10.6MPa。结果表明波纹补偿器原设计厚度的波纹管在未达到其设计压力时即出现屈曲变形,原设计存在缺陷,且径向缺少强化部件及约束,导致补偿器的结构径向刚度不足,致使结构在临界载荷下,波纹管径向弯曲使波纹补偿器整体出现“Z”字型扭曲。
再用取样实测厚度7mm的波纹补偿器结构进行非线性屈曲分析,约束边界条件相同,因8#波纹补偿器出现失稳时内压小于设计压力,因此内压载荷设置为10.6MPa,计算结果见表2,表明当波纹补偿器内压达到5.40MPa的临界载荷时波纹补偿器即出现径向变形屈曲如图6所示。由于壁厚的减薄,加剧了波纹补偿器其径向刚度偏弱的特性,钢管在静水压试验时内部缓慢充水,波纹补偿器内部的压力也随之缓慢增加,当钢管内部达到设计高度921m保压时,因波纹补偿器缺少径向约束部件,径向刚度不足,加之波纹管壁厚小于设计厚度,波纹管受内压力和其他载荷达到某一临界值时突然出现单侧膨胀变形失稳,且钢管在支墩安装槽内缺乏向上的约束,导致波纹补偿器失稳变形时“拉着”钢管的一端使钢管出现脱墩和上拱的现象。结合现场实际情况,试验时充水至设计高度921m时,8#波纹补偿器内静水头为539m内压5.39MPa,在该水头下出现了失稳破坏,与非线性屈曲计算出的临界载荷基本吻合。

图6 实测厚度波纹补偿器内压-位移变化曲线
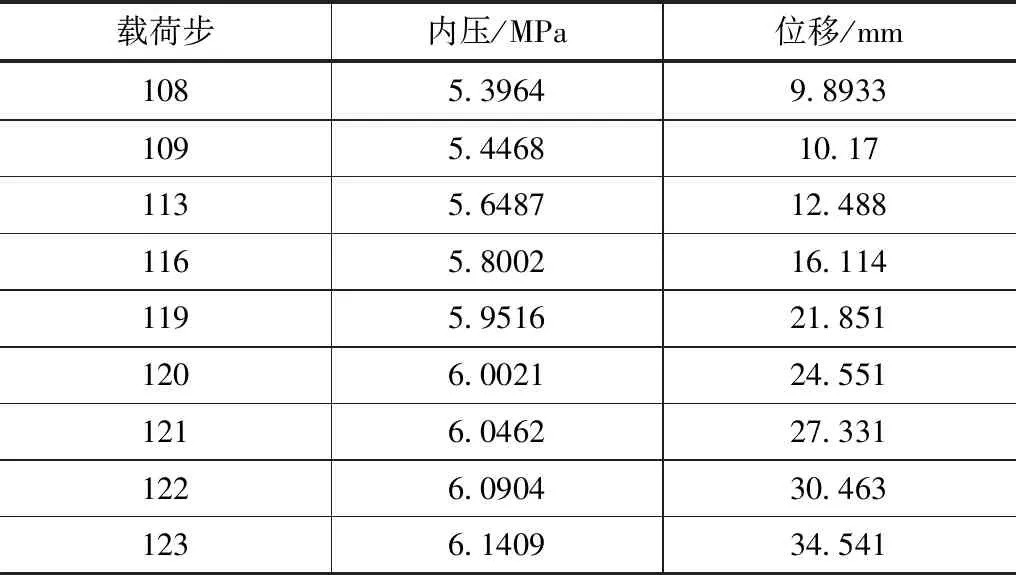
表2 实测厚度波纹补偿器内压-位移变化计算结果数据表
综上所述,波纹补偿器失稳破坏的主要原因是波纹管径向刚度偏弱,影响其承载能力。
4 结语
针对该电站压力钢管波纹补偿器在静载水压试验中失稳破坏并导致钢管脱墩现象,使用基于ANSYS非线性屈曲分析结果表明径向刚度不足是引发事故的主要原因,鉴于此对于引水式电站在波纹补偿器选型时宜优先选用具有径向刚度加强部件的产品,并建议在波纹补偿器与钢管的连接处设置凑合节,以保证其径向刚度。该分析方法成果与现场实际情况吻合,具有显著的工程实用价值,同时对于有限元分析法与工程实际应用结合的理论研究有一定的指导意义。但是压力钢管安装时的轴线偏差、支墩的轴向错位是否也是影响波纹补偿器在内压下失稳破坏的因素,需在后续工作中进一步研究。

