潜深艉轴机械密封热固耦合变形特性分析

王刚伟，王娟，田佳彬，卢明剑，欧阳武，汤敏

(1.武汉第二船舶设计研究所，武汉 430205；2.武汉理工大学 a.智能交通系统研究中心；b.交通与物流工程学院，武汉 430063)

机械密封具有可靠性高、泄露少、功耗低，以及自动补偿等诸多的优点，目前已经在船舶和潜器的轴系密封结构中得到广泛的应用。机械密封的摩擦副之间存在着一层薄薄的介质液膜，动环和静环之间相对旋转形成的动压效应实现动密封。机械密封通过介质压力及补偿机构(通常是弹簧)的弹性力来保持动环和静环间的端面贴合。在理想的工作模式下，机械密封的摩擦副之间充满着一层薄薄的介质液膜，不存在端面的直接接触，这样不仅可以避免或减少密封端面的磨损，同时能够显著减小泄漏量。但是由于介质压力和弹簧力的共同作用，密封端面上会产生机械变形，从而导致端面上的局部接触。在机械密封工作时，端面间的接触摩擦和端面对介质液膜的黏性剪切作用都会产生热量，从而引起密封的热变形；端面上的热变形又通常会导致接触区域的进一步减小，使得密封端面的局部产生高温及高应力的工作状态，进而影响密封的效果和工作寿命。

近年来随着机械密封向高压、高速、高温，以及大尺寸等工作环境拓展其应用领域，上述端面变形和温度之间互相影响和促进的问题愈加严重。对于潜器艉轴机械密封，工作环境更加严苛，其介质压力可达2～10 MPa，摩擦副的热固耦合变形更加显著，是其主要失效形式。相关的研究有通过有限元法对某一型号艉轴密封分别进行了力和热变形分析,结果发现热变形在整体变形中占主导地位。在此基础上进一步的研究表明，受力引起的变形与热变形趋势相反，在内径处产生最大压缩位移，外径处产生最大拉伸位移，而热力耦合变形介于两者之间。有学者考虑了密封在运转前由介质压力导致的端面初始变形，分析端面的温度分布规律，发现初始变形对机械密封最高温度和接触位置均产生一定的影响。有学者通过有限元模型分析了密封摩擦副温度和变形规律及对密封性能的影响，给出了密封摩擦副材料选取的建议。有学者研究动环转速对端面温度的影响，结果表明，转速越高，温度越高；而选取导热系数高的摩擦副材料可有效降低最高温度。有学者针对不同工况下的机械密封进行热固耦合分析得到了摩擦副的变形情况。此外，相关学者针对不同摩擦副材料和摩擦副表面织构对密封温度、变形，以及性能的影响进行了相关研究，比如以合金与青铜材料为密封擦副进行密封性能试验，测试密封端面温度和泄漏量等性能参数；研究摩擦副表面织构对密封变形和性能的影响。

以上研究都主要是针对浅水或轻载工况下的密封变形及性能，而对于深海环境高介质压力下机械密封热固耦合变形的研究相对较少。为此，建立高分子材料/硬质合金为摩擦副材料的某潜器艉轴机械密封的二维热固耦合有限元模型，分析介质压力、摩擦系数、弹簧比压对机械密封温度场和变形的影响。

1 机械密封摩擦副热固耦合模型

1.1 传热模型

机械密封的实际工况通常较为复杂，如果考虑所有的因素进行数值建模往往是不现实的，不仅会增加运算量，有时甚至导致无法进行求解。这里建模基于以下假设。

1)机械密封的结构和载荷均为轴对称。

2)忽略端面对介质液膜黏性剪切作用产生的热量。

3)传热为稳态传热。

4)忽略由于过盈配合产生的附加应力、变形和接触热阻。

根据以上假设和热力学理论，采用柱坐标，机械密封的轴对称稳态热传导微分方程为

(1)

式中：为温度；、分别为轴向和径向坐标。

本模型需满足传热学的三类边界条件。

1.2 热流密度

机械密封的温度升高和热变形通常主要来自端面接触的摩擦热。从数量级来看，接触面微凸体层的厚度与密封的尺寸相差交大，因此可以忽略，故本研究中摩擦热加载采用表面热，即施加第二类热边界条件。在机械密封实际工作时，摩擦热同时产生于密封的静环和动环端面，其总的热流密度可通过下式进行计算。

()=()

(2)

式中：()为半径处的总热流密度；为摩擦系数；()为半径处的接触压力；为动环旋转角速度。

摩擦热在动环和静环间的分配往往较为复杂，受到材料、结构等诸多因素的综合影响。在稳态工作时，密封端面间能够充分进行热传导，且本文忽略接触热阻的影响，故认为接触区域的温度基本相等。通过有限元法进行模拟时，可以通过在接触面上施加极大的接触导热率来实现，将接触导热率设置为109·W/(m·K)数量级。

1.3 对流换热系数

介质与密封间的对流传热会带走一部分热量，因此需要在模型中施加第三类边界条件。介质相对于动环的流动主要包括旋转流动和轴向流动，其间的对流换热系数可按下式计算。

(3)

静环与介质间的对流换热系数可按下式计算。

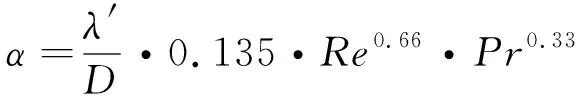
(4)

1.4 热固耦合计算

根据式(2)，计算密封静环和动环端面上的热流密度需要已知接触应力。因此，热固耦合计算按如下。

1)不加热流密度，通过模型计算端面接触应力。

2)根据式(2)计算各节点的热流密度并施加到模型上，重新计算温度场和应力场。

3)检查两次计算得到的接触应力，若满足式(5)则为收敛，停止计算。

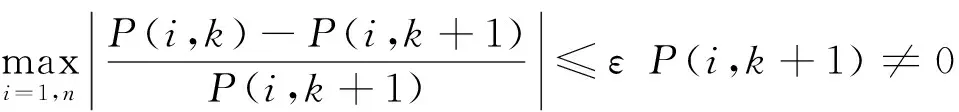
(5)

式中：为密封端面上节点个数；(,)为在第次计算后端面上第个节点的接触压力；(,+1)为在第+1次计算后端面上第个节点的接触压力；为给定的精度值，通常取0.001。

4)如不满足收敛条件，则根据本次得到的接触应力按照式(2)重新计算热流密度，并重复步骤2)和3)。

以上计算过程，第一次求解是为了获得接触应力来计算所需的热流密度，后面的求解过程则是为了提高接触应力和热流密度的计算精度。

2 有限元模型

根据上述的假设和建模思路，通过软件ANSYS建立机械密封环的轴对称热固耦合有限元模型，见图1。

图1 机械密封环有限元模型

其中左侧为动环，右侧为静环。模型中，静环和动环均采用热-结构耦合单元PLANE223。对于端面间的接触，静环接触面采用接触单元CONTA172，动环接触面采用目标单元TARGE169。为提高计算精度，将接触附近的网格相对细化。通过网格无关性验证，并综合考略计算效率，确定单元数为4 150。

机械密封环的主要尺寸见图2和表1。

图2 机械密封环主要尺寸

表1 密封结构尺寸 mm

摩擦副材料和介质的物性参数见表2和表3。

表2 摩擦副物性参数

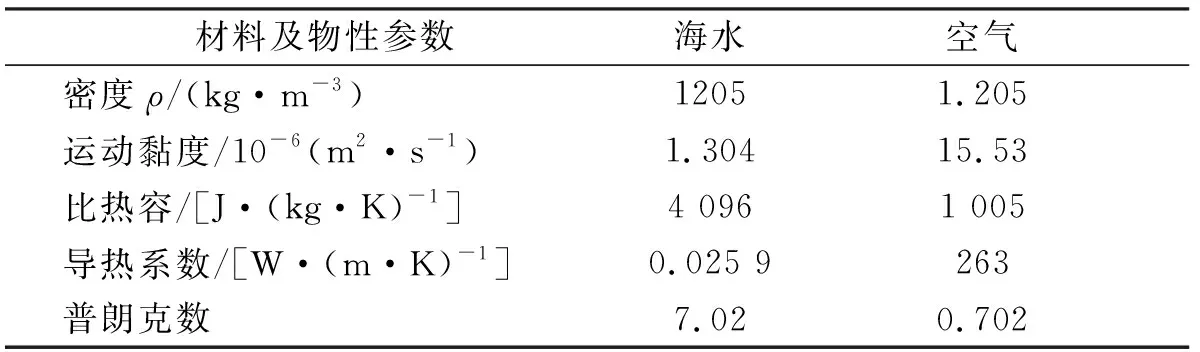
表3 海水和空气物性参数

其中，静环采用高分子材料飞龙T12，海水温度为4 ℃，密封侧空气温度为25 ℃。

边界条件的设置见表4,其中边界的符号见图2。接触面间的液膜压力近似为斜坡载荷，即按介质的压力线性施加在接触面上。

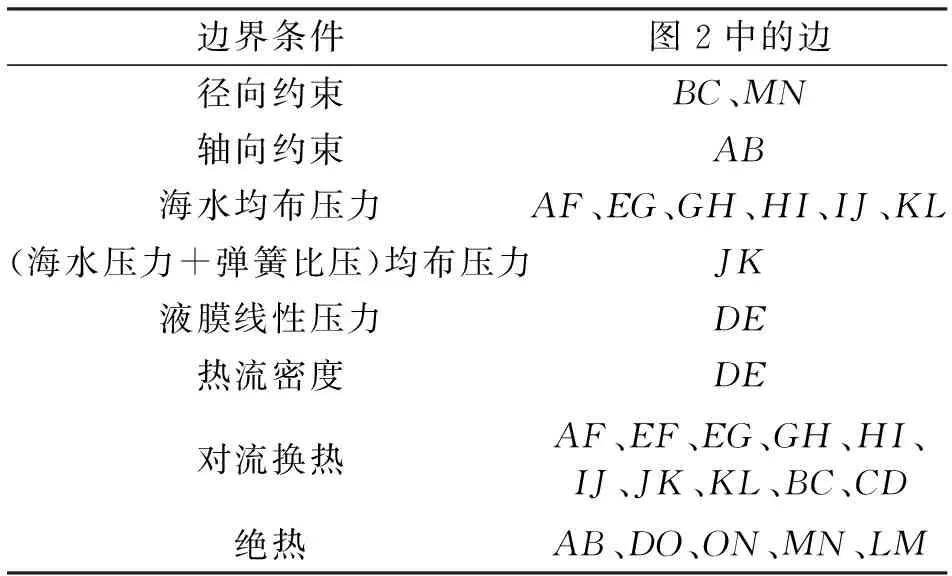
表4 边界条件

3 计算结果及讨论

为了方便比较和研究介质压力、摩擦系数等参数对机械密封温度和热变形的影响，选取介质压力4 MPa、摩擦系数0.1、弹簧比压0.2 MPa、转速200 r/min为参考工况。分析每一种参数的影响时只改变所研究的参数，且保持其他参数不变。

3.1 介质压力的影响

本文研究的机械密封工作在深水的海水中，对应的介质压力较高，因此对密封性能的要求也必然较高。通过以上热固耦合模型计算，密封环在参考工况下的温度云图见图3。

图3 温度云图

由图3可见，密封环的最高温度为92 ℃，发生在接触面靠近内径位置处。动环整体的温度均有显著的升高，而静环仅在接触端面附近有局部的温升，这主要是由于动环的导热系数较大的缘故。变形云图见图4。

由图4可见，最大变形发生在静环接触面内径边缘处，与产生最高温度的位置对应。动环与静环接触面呈锥形，仅靠近内径附近存在接触。

图4 变形云图

静环和动环接触面上轴向位移随介质压力的变化见图5，其中节点号是按接触面外径向内径的顺序。

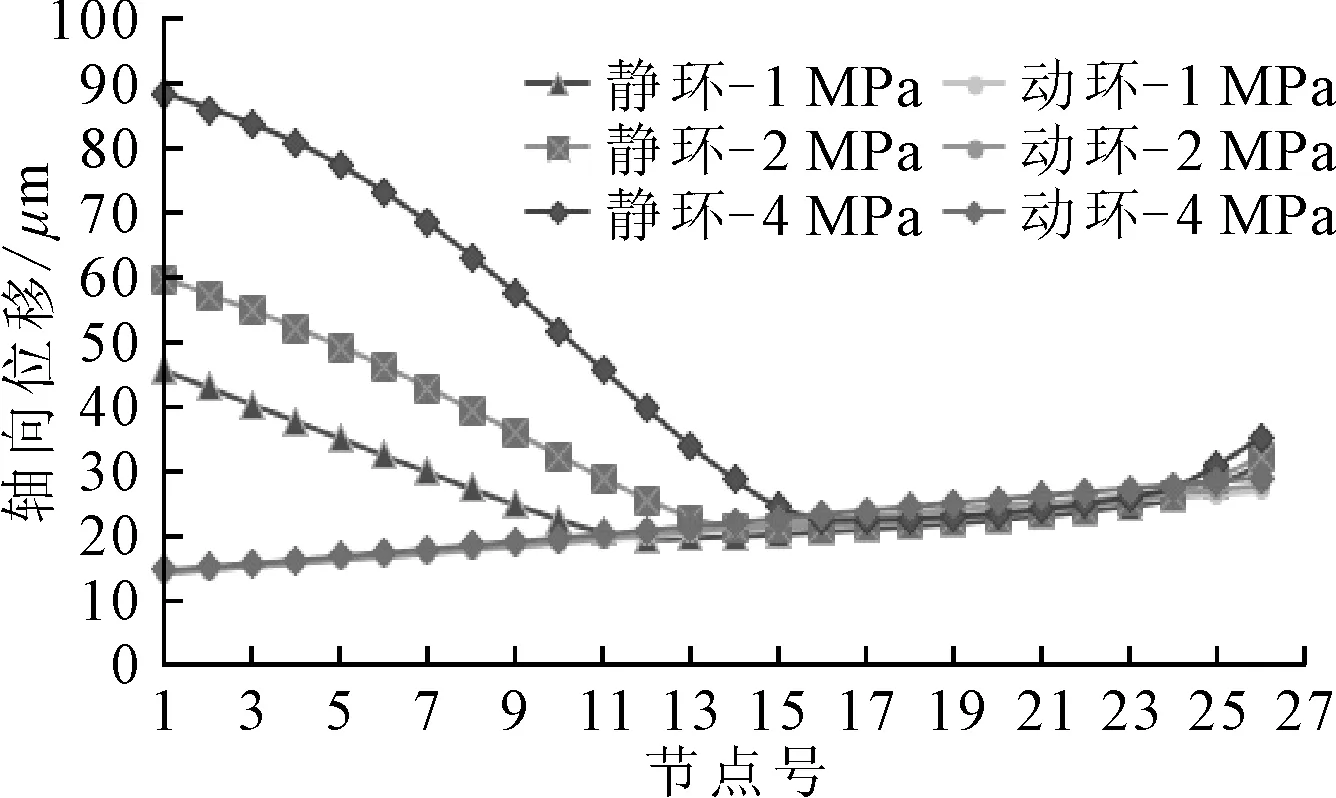
图5 接触面轴向位移随介质压力的变化

由图5可见，在特定的介质压力下，静环接触面的轴向变形沿着外径到内径方向上先逐渐减小，然后再逐渐增大；在转折点处以前的变形大于动环对应位置的变形，这是由于静环的弹性模量较小的缘故；动环接触面的轴向变形近似呈线性逐渐增大。在转折点以后，动环与静环的轴向变形基本相等，即端面相接触。随着介质压力的升高，静环端面未接触区域的轴向变形逐渐增大，而动环的轴向变形则基本不变，即端面锥形开口显著增大，密封的性能下降。

摩擦副上的接触应力随着介质压力的变化见图6。

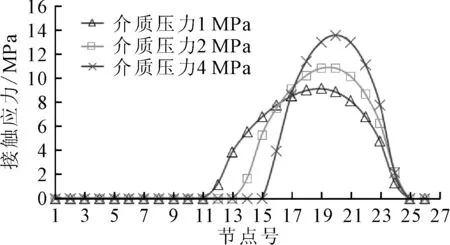
图6 接触应力随介质压力的变化

由图6可见，在特定的介质压力下，接触应力最大值发生在接触区域的中间部位。随着介质压力的增大，最大接触应力也随之增大，但接触面积逐渐减小。

不同介质压力下最高温度见表5。由表5可见，随着介质压力的增高，机械密封的最高温度逐渐增大，但增幅不大。这是因为虽然介质压力增大导致接触应力增大，但接触面积的减小导致产生的总热量并没有显著增大。

表5 最高温度随介质压力的变化

3.2 摩擦系数的影响

高分子材料T12的摩擦系数在0.04～0.16之间，计算不同摩擦系数下机械密封的温度和变形。接触面轴向位移随摩擦系数的变化见图7。

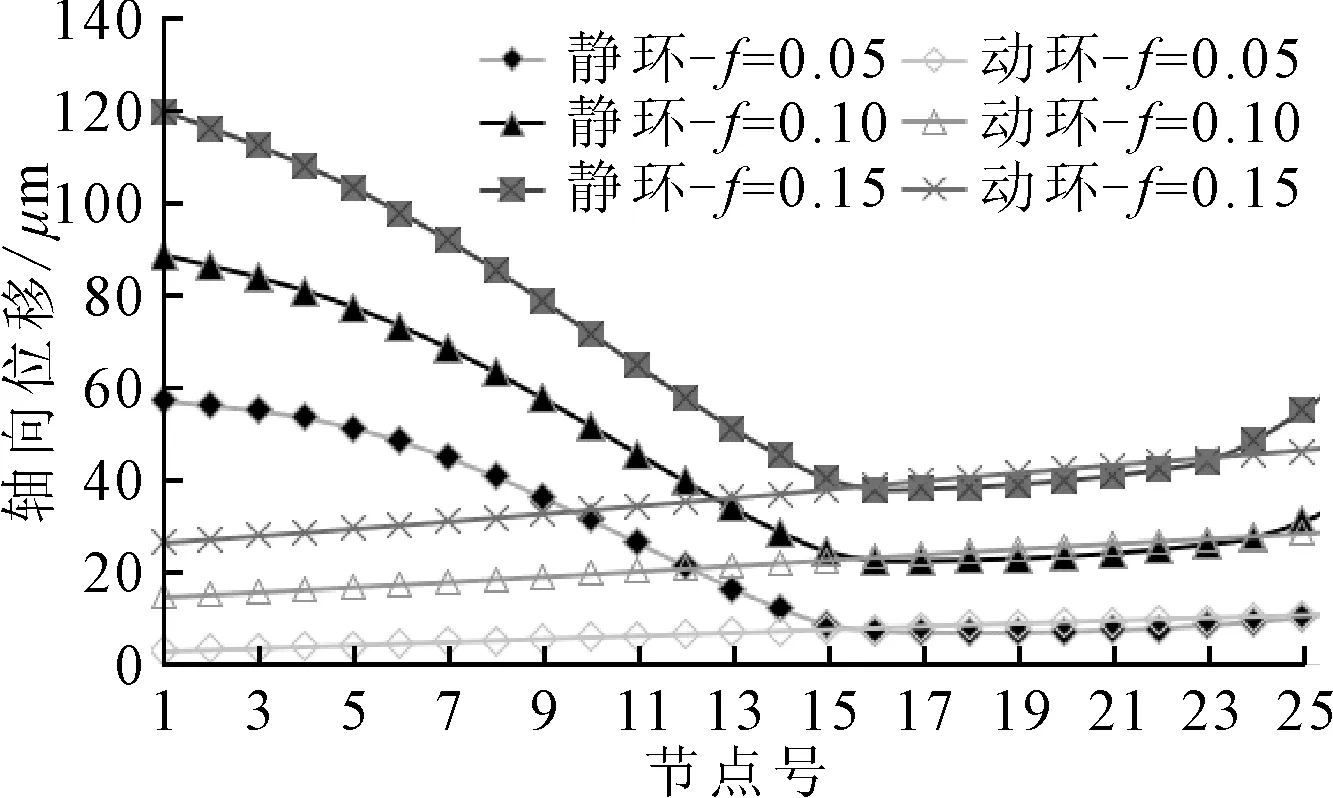
图7 接触面轴向位移随摩擦系数的变化

由图7可见，在特定的摩擦系数下，动环和静环接触面上的轴向位移变化趋势同图5。随摩擦系数的增大，动环和静环接触面上的轴向位移均增大。这是由于摩擦系数增大导致摩擦热增加，从而导致静环和动环较大的热变形。

接触应力随着摩擦系数的变化见图8。

图8 接触应力随摩擦系数的变化

由图8可见，在特定摩擦系数下，接触应力最大值发生在接触区域的中间部位。随着摩擦系数的增大，最大应力发生的位置逐渐向趋向外径；此外，最大接触应力逐渐增大，接触面积虽略有减小，但大体保持不变。

机械密封最高温度随摩擦系数的变化见表6。

表6 最高温度随摩擦系数的变化

同表5相比，随着摩擦系数的增大，最高温度显著增大。这是由于随着摩擦系数增大，热流密度增大，而接触面积基本不变，导致产生的摩擦热显著增加。在摩擦系数为0.15时，接触面上最高温度达到138.2 ℃，会造成端面间的液膜汽化，从而引起密封稳定性降低，泄漏量增加。

3.3 弹簧比压的影响

轴向位移随弹簧比压的变化见图9。

图9 轴向位移随弹簧比压的变化

与图5和图7进行对比，轴向位移随弹簧比压的变化规律与随摩擦系数的变化规律更相似。

不同比压下接触应力的变化见图10。

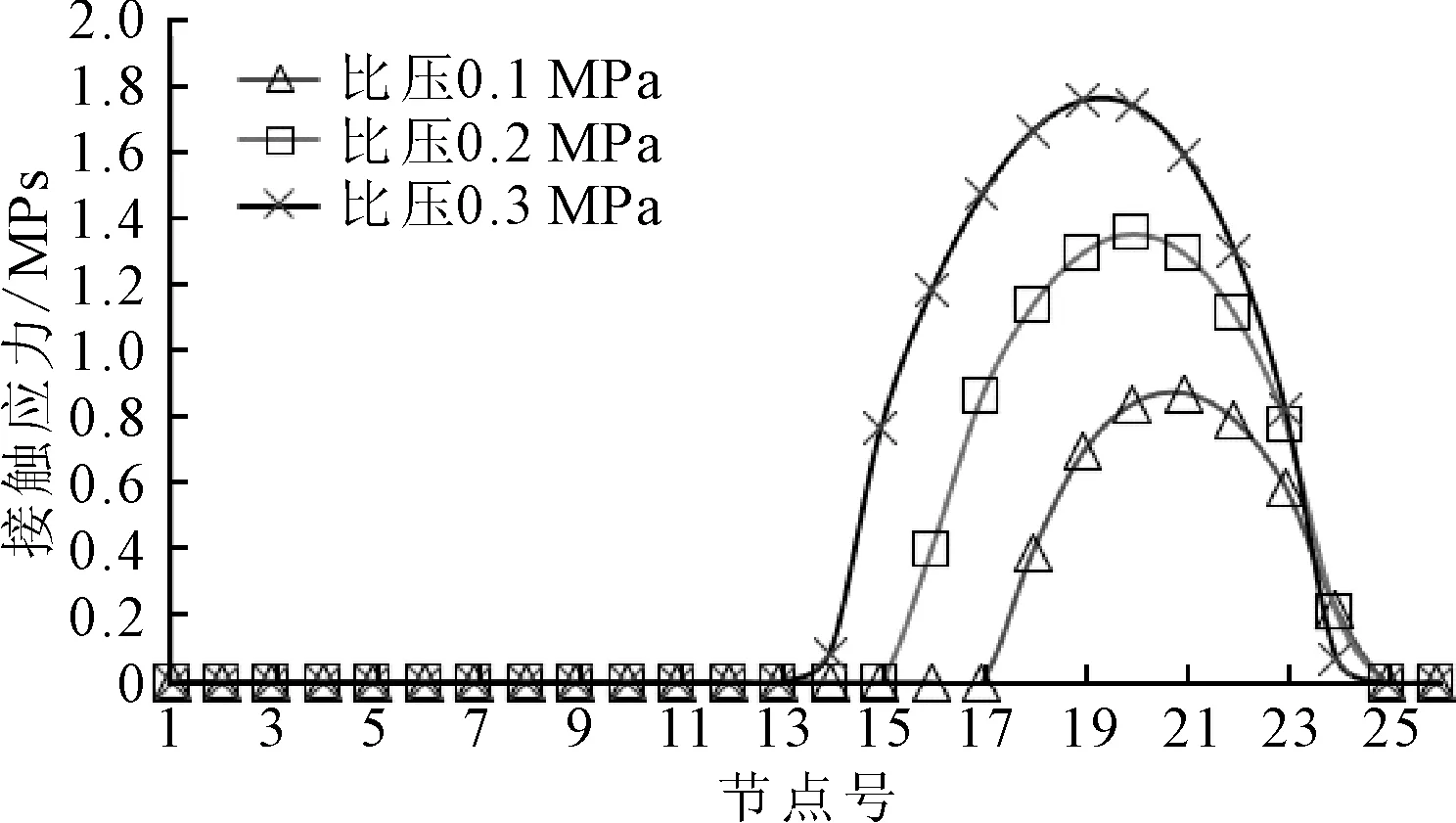
图10 接触应力随弹簧比压的变化

由10图可见，接触压力随着弹簧比压的增大而增大，且最大应力发生的位置逐渐向趋向外径；接触面积也随之略有增大。对比图6和图10可见，同样是施加在机械密封上的均匀压力载荷，介质压力和弹簧比压对机械密封接触的效果显著不同。

不同弹簧比压下机械密封的最高温度见表7。

表7 最高温度随介质压力的变化

由表7可见，随着弹簧比压的增大，机械密封的最高温度也逐渐升高。这是由于随着弹簧比压的增大，接触应力和接触面积均增大，因此导致摩擦热增加。其中比压为0.3时，接触面的高温会造成端面间的液膜汽化。

4 结论

1)最大接触应力发生在接触部位的中间部位，且随着介质压力、摩擦系数和弹簧比压的增大而增大；但介质压力、摩擦系数和弹簧比压对接触面积的影响不同，因而摩擦热不同，导致热变形规律上的差异。

2)机械密封最高温度发生在端面内径附近；随着介质压力、摩擦系数和弹簧比压的增大，机械密封的最高温度也随之增大，但摩擦系数和弹簧比压引起温升相对更大，这是由于接触部位热流密度相对更大的缘故。

3)由于静环弹性模量较小，介质压力的增大导致静环未接触部位的轴向变形增大，但对动环的轴向变形基本没有影响；随着摩擦系数和弹簧比压的增大，静环和动环的轴向变形均随之增大。综合分析结果可见，在潜深艉轴密封的设计中必须尽量降低摩擦副的摩擦系数并选取适当的弹簧比压。