基于有限元网格的液货体积计算方法

李洛东，刘成名

(中国船级社 海洋工程技术中心，天津 300457)

在对船舶海工浮式结构物进行有限元分析时，常常会利用面压力来模拟液舱的装载和外壳的浮力。但由于有限元网格与常规的液舱舱容计算软件的几何信息不能完全匹配，压力合力产生的液货质量和浮力均与装载手册存在较大的差异，从而导致力不平衡现象，影响结构分析结果的准确性。在舱容研究方面，张俊研究了板架变形导致液舱变化后船舶液货舱舱容修正技术。陶美金等研究了拱垂度舱容货舱舱容体积修正的关联关系，提出液货船结构变形曲线快速计算方法。项勇等研究了用全站仪对船舱进行分段精确测量，建立舱室数学模型，采用B样条方法拟合，形成数学舱图，利用Matlab计算液货舱容。胡敏捷等提出了一种基于地面三维激光扫描测量，重建舱室三维模型来实现舱室容量计量的新方法。以上舱容的计算方法均是基于舱容计算软件或通过对大型的曲面进行积分的计算方法。而有限元的几何信息不同于舱容计算软件，其几何信息是离散的三角形或四边形网格。对于基于网格的液体体积计算，需要对于网格单元法向的判断和分析，明确单元的两种法向的，即朝外和朝内。胡毕等提出了通过拓扑信息和两个网格单元在公共边上的首末顶点编号相反的原则，对网格单元顶点在单元中重新编号的方法，将所有单元的法向调整一致。该方法也可用于对于网格单元的法向判断。综合以上研究，提出基于有限元网格的舱容计算方法，通过对液舱表面的网格单元及关联节点的几何拓扑信息分析、向量运算等手段，计算得到液舱的舱容表，为有限元分析中液舱压力精确模拟、船舶浮态调整、静力平衡等提供数据基础。

1 基于网格的液货体积计算方法

1.1 方法描述

对于任何连续湿表面网格的液舱单元，其在液舱装载情况下的体积均可通过面积和距液面高度的积分获得。

对于距液面高度的计算，当船舶处于正浮状态下，其距离液面的位置可以通过单元的坐标值进行计算。一旦船舶发生纵倾、横倾时，则距离液面的距离就不能单纯通过其坐标位置判断，需要通过液面所在的平面的垂向距离进行判断。针对于所有状态下的液货体积或排水量的计算，则可通过引入相对高程来进行估计。此相对高程为舱室内任意参考点的指定倾斜或非倾斜液面下的垂直于液面的单位向量，通过向量计算获得到液面的距离。

对于面积计算，可通过计算单元的面积，计算单元的法向以及垂直于液面的单位向量进行向量计算，获得在垂直于液面的单位向量下的投影面积。

此方法仅适用于所有网格单元法向一致的情况，即液舱/外壳网格单元的法向均朝外或朝内。但有限元网格一般多个液舱相邻，其网格单元的法向不一致。

综上所述，若计算液舱的液货体积或外壳的排水量，需要完成如下步骤。

1)液舱/外壳网格单元的法向分析。

2)网格单元的相对高程计算。

3)网格单元投影面积计算。

4)液货体积/排水量及重心计算。

计算流程见图1。

图1 计算流程

1.2 网格单元法向几何拓扑分析

对于任何连续的网格单元，其法向均遵循右手定则，可以通过其节点顺序和其相邻单元的节点顺序对网格单元的法向进行判断。其几何拓扑结构比较简单，但是需要对大量的网格拓扑信息进行分析。

可设定任意1个网格单元的法向已知为朝外或者朝内，搜索其相邻的单元，如其共边的单元节点的顺序为相反，则法向一致，反之亦然。通过逐步扩散的方法直至得到所有单元的法向信息。网格单元的法向及其搜索方法见图2。

图2 网格法向搜索方法示意

图2中虚线框为起始网格，2表示第2次搜索获得的网格，3表示第三次搜索得到的网格，以此类推。灰色填充表示与起始网格的法向相反，无填充表示与起始单元的法向相同。如采用程序对单元的法向进行分析，其程序流程见图3。

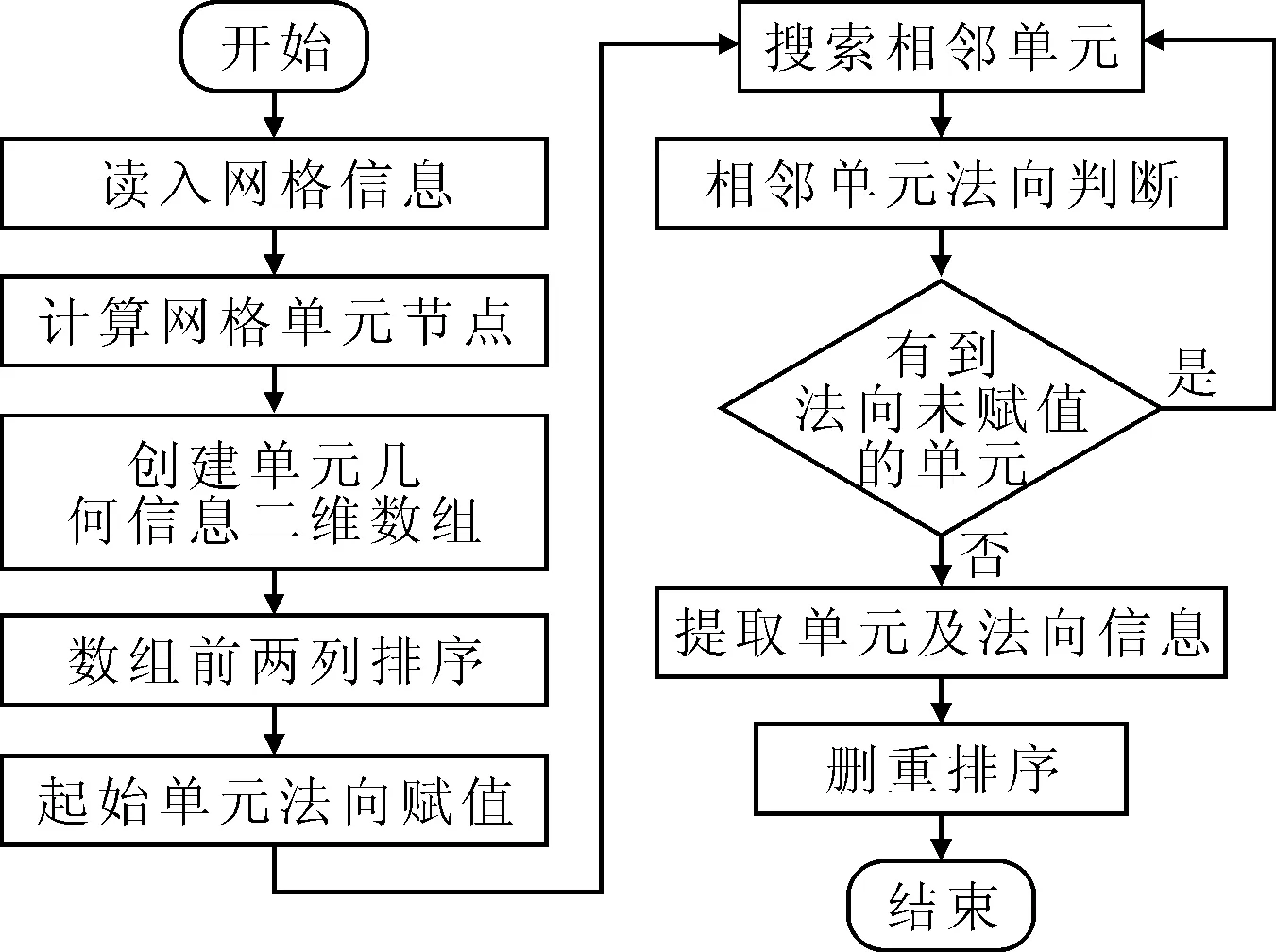
图3 网格法向搜索流程

1.3 相对高程hi的计算方法

相对高程为网格至参考点所在液面的距离，该量为标量。其计算步骤如下。

1)选择任意一点作为参考点。

2)计算液面向量。

垂直于液面向下的向量可以通过液面平面内的3点的坐标计算。

=×

(1)

式中：为点到的向量；为点到的向量。

对向量进行归一化，计算得到标准化垂直于液面向量。

=||

(2)

式中：为垂直于液面向量；||为向量的模，如果船舶处于正浮状态，=(0,0,-1)。

3)计算液舱参考点到网格单元的向量，按照下式计算。

=((1)，(2)，(3))

(3)

式中：为参考点到单元的向量；为网格单元中心的坐标值，m；为参考点的坐标值，m。

4)计算液舱的值，等于2个向量的点乘值。

=·

(4)

式中：为参考点到单元的向量；为标准化的垂直于液面向量；

根据向量点乘的物理意义可知，2个向量点乘，如果一个向量的模为1.0，点乘后的值就为另1个向量到单位向量的投影长度。从4图示可见：长度正好等于。该公式可应用于三维空间，不受任何限制。的计算见图4。

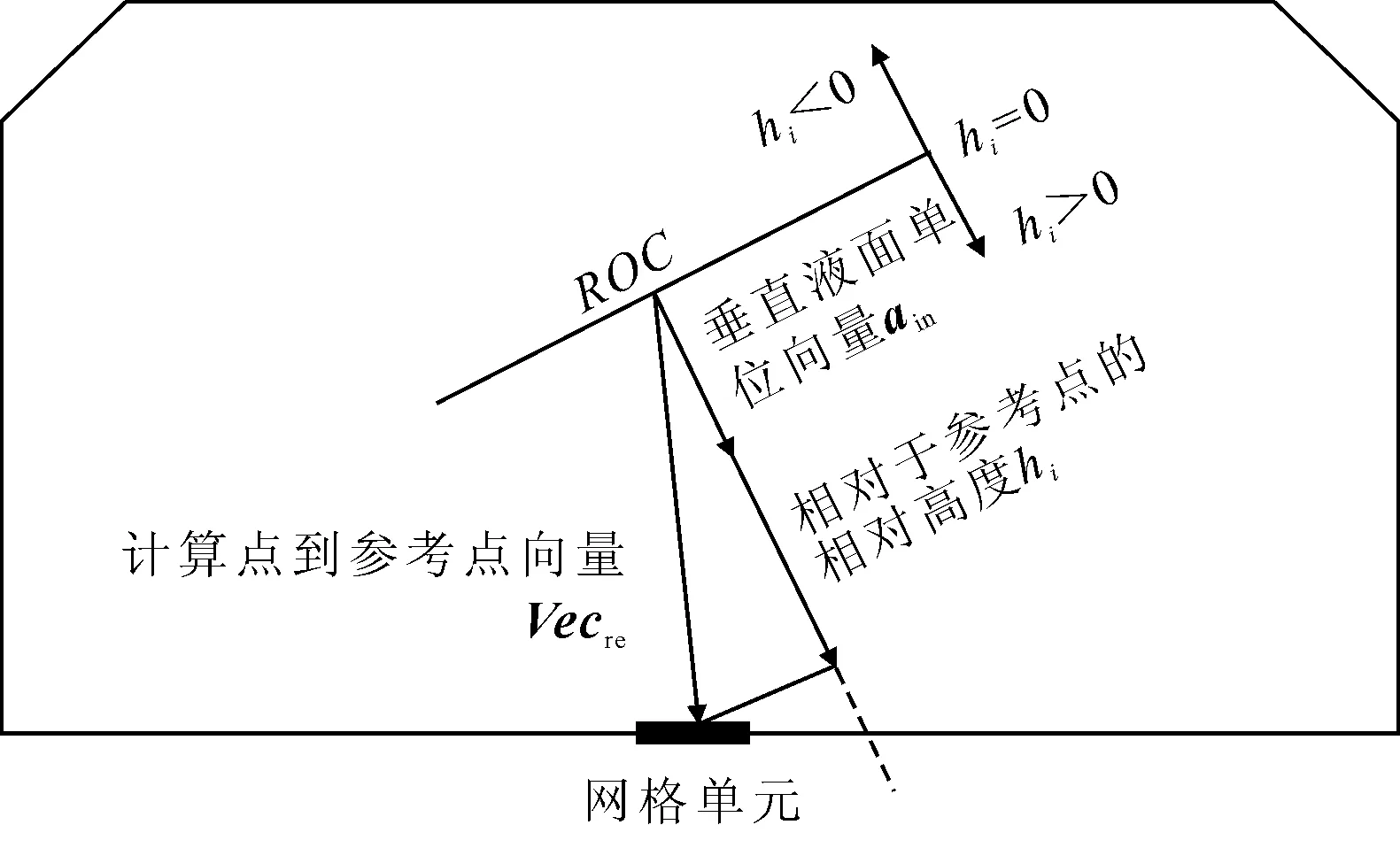
图4 网格单元相对高程hi的计算方法示意

满载情况下应从倾斜后的液面最顶点计算，而对于不规则舱室对顶点的位置未知。历遍舱室组的所有网格单元，找到最的最小值，在之后的计算中减去最小值即是到顶点的距离。

1.4 网格投影面积As的计算方法

网格投影面积需要根据其法向与液面向量的运算进行计算获得。假定液舱/外壳的单元均朝外。那么当网格单元的法向与液面的向量夹角大于90°时，计算获得的面积为负值，计算得到的体积也为负值。从物理意义上讲，部分液舱边界的顶部在液面以下，则需要扣除其体积，最终计算的液货体积值为所有网格单元体积之和，投影面积的计算见图5。

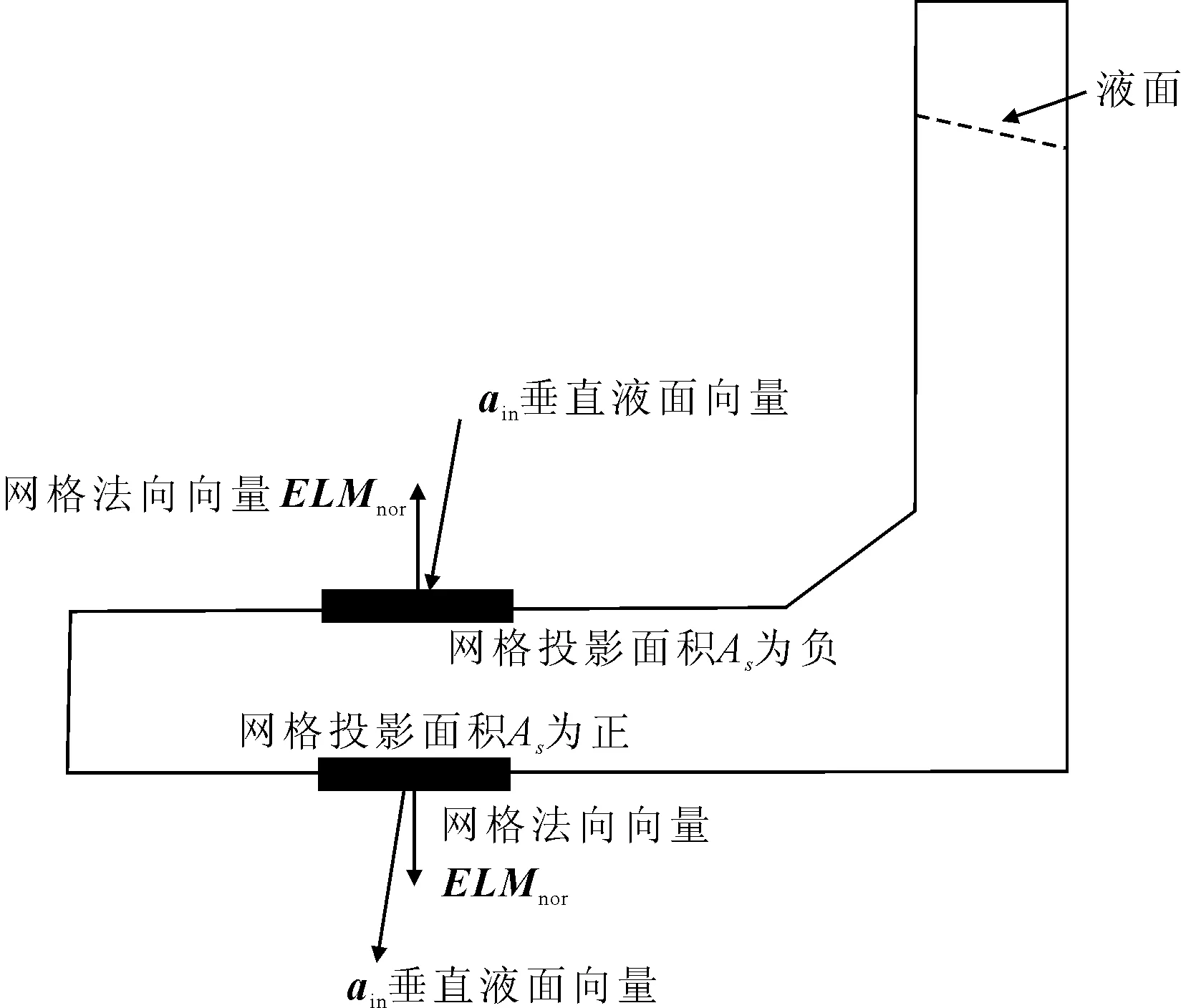
图5 网格投影面积As计算方法示意

1)计算单元的法向向量，可以通过两个向量叉乘的方式计算。

=×

(5)

式中：为网格单元第一条边的向量；为网格单元第二条边的向量。

2)对单元法向向量进行标准化处理，计算得到。

3)计算矢量面积值。

=A··

(6)

式中：为单元的面积，m；为标准化法向向量；为标准化的垂直于液面向量；为单元朝向因子，法向朝外取1.0，朝内取-1.0，根据.单元法向分析结果确定。

1.5 设定不同液面位置的计算步骤

1)获得所有单元最大、最小的。

2)从最小到100等份；最小值在为舱顶的位置，为负值。

3)计算不同的液位下的液货体积。

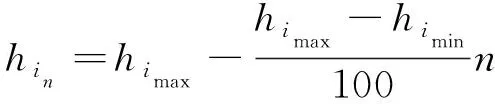
(7)

式中:为所有网格单元的最大值，m；为所有网格单元的最小值，m；为1～100的正整数。

1.6 计算不同的hin液位下的液货体积计算步骤

1)根据获得所有单元的有效面积、有效距离进行历遍。

2)如果单元的大于，该单元为液面下单元。

3)计算单元积分的体积值elm，由于的影响，elm可能为负值。

elm=(-)

(8)

式中：为单元标量面积，m；为单元的相对高程，m；为设定的液面高程，m；为标准化的垂直于液面的向量。

4)液货体积为所有的网格单元体积的和。

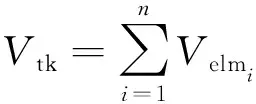
(9)

式中：elm为第个网格单元的体积，m。

1.7 不同的hin液位下的舱室重心计算方法

计算在不同液位下的舱室重心有效容积，按如下步骤计算：

1)根据获得所有单元的有效面积、有效距离进行历遍。

2)如果网格单元的大于，该单元为液面下单元。

3)计算网格单元积分的体积值elm，见.。

4)计算每个网格单元液体的重心位置。

(,,)=

(,,)-(-)·/2

(10)

式中：()，()，()为单元的中心处的坐标，可通过3个节点求和平均，m；为单元的相对高程，m；为设定的液面高程，m；为标准化的垂直于液面的向量。

5)计算液货体积，见1.6。

6)计算当前液位下的舱室重心：

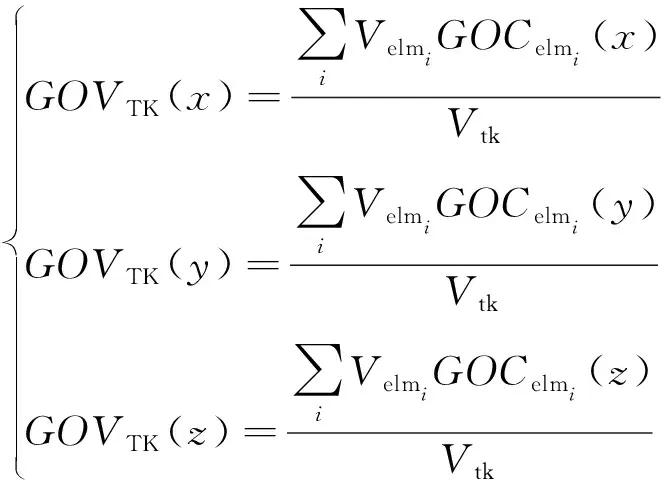
(11)

式中：为第个单元的体积，m；为单元液体重心位置坐标，m；为液面位置下的液货体积，m。

2 计算实例

2.1 液舱液货体积计算

以某油船大型液舱为例，计算其液货体积。目标舱为货油舱，舱容为10 645.29 m网格模型见图6。

图6 液舱网格模型

计算得到满载舱容为10 643.64 m，与装载手册的误差为0.016%。计算不同液位下的舱容，与装载手册中的舱容对比，误差均在0.02%之内，两者舱容对比见图7，重心位置对比见图8。对比结果表明，该算法可行，计算结果准确。

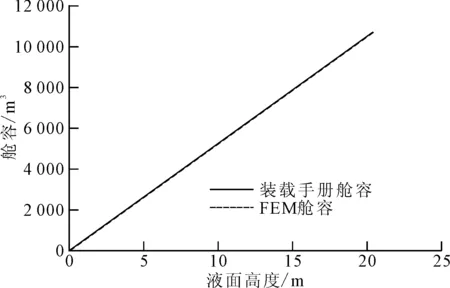
图7 液货体积对比

图8 计算重心位置与装载手册数据对比

2.2 排水量计算

以某油船的外壳网格为例，计算其舱容。该船满载排水量为127 616.99 m，目标外壳湿表面网格见图9，计算多个液位下的液货体积和液舱重心位置。

图9 外壳湿表面网格模型

计算得到的满载排水量为127 365.6 m，与装载手册的误差为0.20%。将计算所得不同吃水、正浮状态下的舱容与装载手册的舱容进行对比，误差均在1%之内。两者排水量对比见图10。重心位置对比情况见图11。

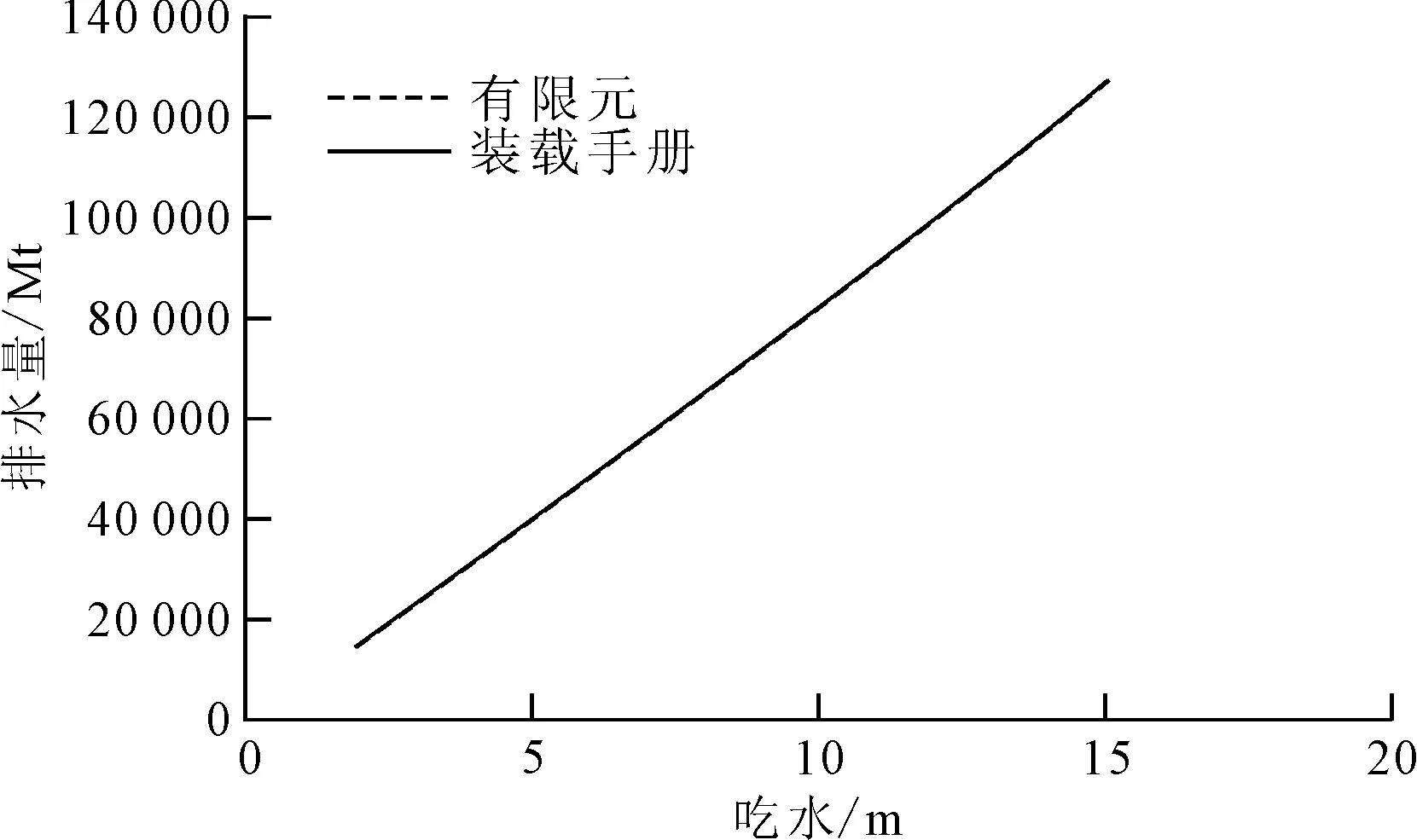
图10 排水量对比

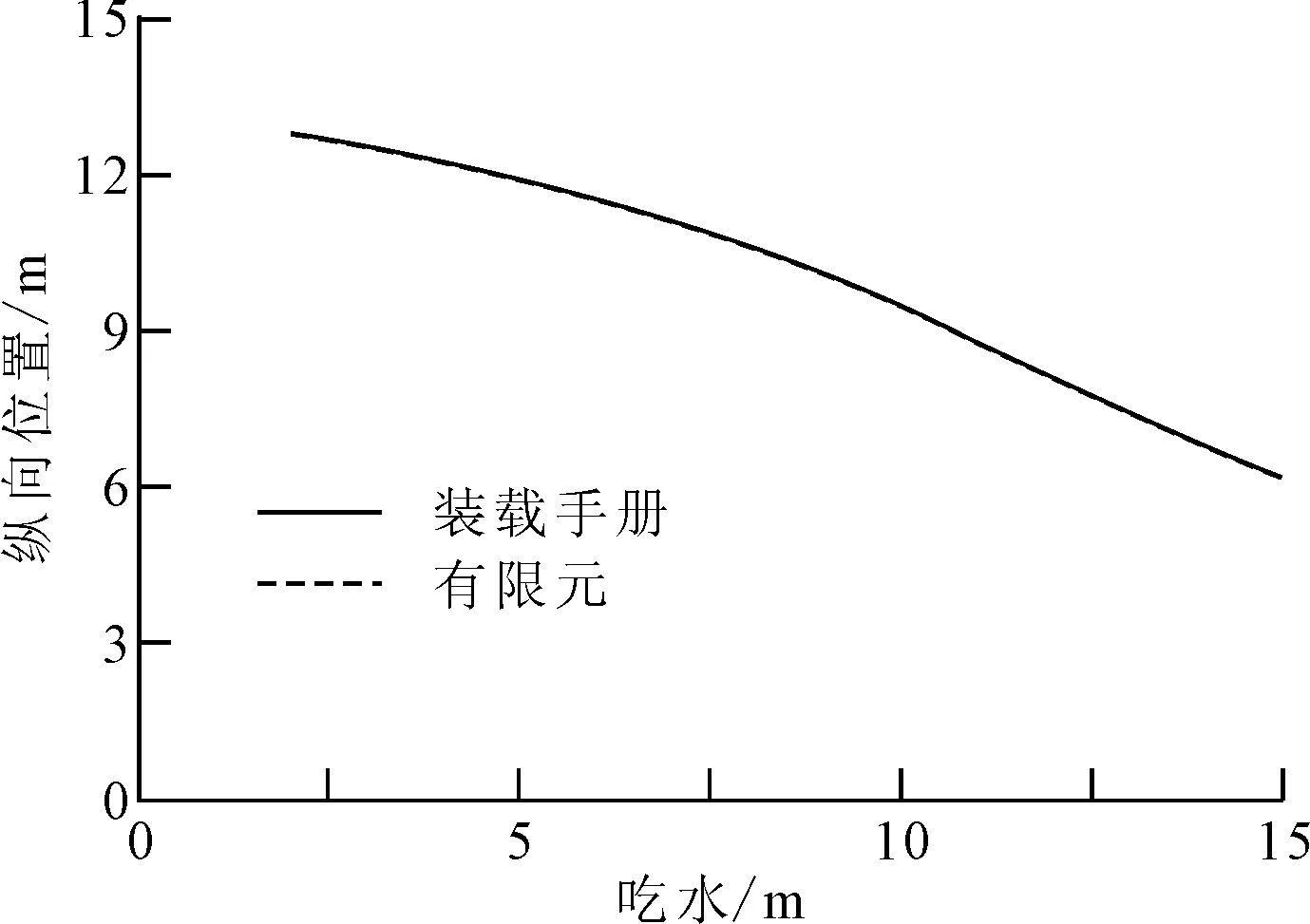
图11 浮心纵向位置对比

利用该算法计算艏倾状态下的排水量，该工况艉部吃水14.731 m、艏部吃水15.172 m，得到排水量为127 378.78 m，装载手册的排水量为 127 603.61 m，误差为0.177%。

以上数据表明该算法可行，计算结果准确，计算得到的不同吃水的排水量误差在2‰之内，完全符合有限元分析的要求。

3 结论

1)基于有限元网格的容积计算方法可行，计算结果准确。

2)该方法可扩展用于所有的水密舱室在任何倾斜状态下的液货体积计算。

3)通过该方法可以对有限元舱室和排水量进行分析，校准有限元在几何尺度上的误差，相关数据可用于后续的静力平衡分析。

4)目前规范的压力计算均针对于满舱的计算，对于其他装载形式如FPSO液舱长期处于半载状态，该算法可通过等体积法确定在运动状态下的压力载荷分布。