风险相依、风险溢出与保险机构系统重要性评估
陈奇柏 雷振华
(中国联通智能城市研究院,河北保定 557707;南华大学经济管理与法学学院,河北保定 557707)
一、引言
在金融中的保险往往是受到忽视的,但保险业的保障功能够有效地推进“六稳六保”,对金融市场的稳定和社会经济的发展具有重要的意义。相对其他金融机构而言,传统意义上保险机构的系统性风险相对较低,但同时保险机构作为资本市场中的重要投资者,近年来不断涉及非保险业务,这提高了保险机构和其他金融机构和金融市场的业务关联度,导致保险机构面临着潜在的自身风险和风险传染问题。因此,保险机构和保险业作为重要的主体,同时存在金融风险的现状,本文从保险机构和保险行业的视角,分别分析保险机构和保险业之间的风险相依和风险溢出,以期挖掘其风险特征,进而实现风险防控的目的。
对于风险相依结构,相比于网络分析、Granger因果检验、DCC-GARCH模型和Pearson相关系数等相关性方法,Copula模型能够描述序列间非线性和非对称的相关性。等(2014)认为尾部相依度对极端风险事件和状况的刻画更加精准,而Copula函数能够较为准确地去度量包括上尾和下尾的尾部相依度。王培辉(2016)使用Markov时变Copula研究了我国银行业、保险业、证券业和信托业之间的尾部动态依存结构,综合运用混合Copula和时变Copula,以反映金融市场时变性、厚尾性和非对称性等复杂特征。Mejdoub和Arab(2018)使用D-Vine-Copula模型来分析保险机构四种非寿险损失的相依结构,认为Vine-Copula模型能够准确地刻画高维金融变量之间的相依性。综上所述,对于风险相依,Copula模型能够准确刻画和捕捉序列间的尖峰厚尾、波动聚集、有偏非对称依存结构等金融特征,特别是极端事件下的尾部依赖。
对于风险溢出效应,国内外学者主要使用CoVaR、MES、SRISK和CCA等模型。其中,CoVaR是系统性金融风险的主要模型,主要研究当某个金融机构陷入危机时,整个金融市场面临的风险水平。王周伟等(2014)指出CoVaR模型的估计方法主要包括分位数回归、DCC-GARCH和Copula等,并分析了各个估计方法的优缺点。欧阳资生和莫廷程(2017)通过分位数回归来估计改进的CoVaR模型,研究了上市商业银行之间的风险溢出效应。严伟祥等(2017)使用DCC-GARCHCoVaR模型,研究了银行业、证券业、保险业、信托业以及金融期货之间的风险溢出效应。翟永会(2019)使用时变t-Copula-CoVaR模型,分析了我国各个实体行业与银行业之间的动态风险溢出效应,考虑了各个市场之间时变性、非线性和波动聚集性。综上所述,DCC模型综合考虑了金融时间序列之间的非线性、时变性、聚集性和联动性等复杂的风险相关关系。
二、模型构建
(一)GJR模型
研究保险机构和保险业的风险相依性,以及保险机构对保险业的风险溢出效应的前提是选择合适和准确的边际分布模型。大量的历史数据和经验表明,金融时间序列存在有偏、尖峰、非正态和非线性等特征,不适合普通的回归模型。GJR模型能够较好地解决金融时间序列中的自回归、波动聚集和非对称效应等问题,故本文使用GJR模型来拟合和刻画各个收益率序列的边际分布,该模型主要包括均值方程模型、方差方程模型和残差分布模型。
(二)Copula模型
相比于Pearson相关系数,Copula能够刻画序列之间的非线性、非对称性和厚尾性等复杂特征,且不需要考虑边际分布的各种形式,故本文选择Copula模型来描述各个保险机构和保险业之间的风险相依结构。
Copula函数能够将联合分布和其对应的边际分布连接起来,故Copula模型的重点在于最优Copula函数和边际分布模型的选取,其中常见的Copula函数主要有Gaussian Copula、Student's t Copula、Gumbel Copula、Frank Copula、Clayton Copula和SJC Copula等。
(三)DCC-CoVaR模型
CoVaR模型的估计方法主要有分位数回归、DCC-GARCH模型和Copula模型等,相比于其他估计方法,DCC-CoVaR模型能够准确地描述各个保险机构和保险业之间的非线性和时变性等风险特征,强调风险波动的聚集性,故本文选择GJRDCC模型来估计CoVaR模型。
为了准确地刻画保险机构发生的极端事件,本文参照Girardi和Ergün(2013),对保险机构的危机条件进行了改进,以反映其尾部特征。改进的CoVaR模型定义如下:
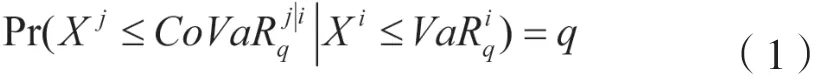
对于DCC-CoVaR模型,本文对式(1)进行转化可以得到:
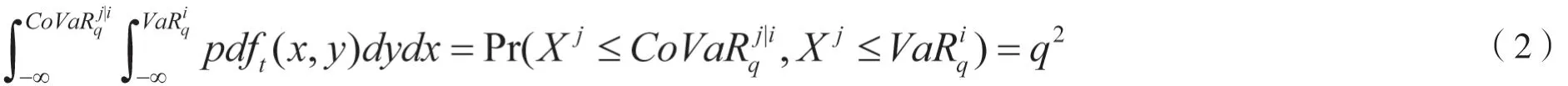

三、实证结果与分析
本文主要研究保险机构和保险业之间的相依程度以及保险机构对保险业的风险溢出效应,研究对象主要是各个保险机构和保险业。对于保险机构数据的选取,本文考虑数据的可获性和完整性,使用A股上市的保险公司来代表保险机构,主要包括中国人寿、中国平安、中国太保和新华保险,这四家保险公司构成了我国保险机构的主体,均入选国内系统重要性保险机构(D-SII)。对于保险业,目前国内学者还未形成统一和科学的数据标准,本文考虑数据的关联性和代表性,通过中国人寿、中国平安、中国太保和新华保险等4家保险公司的加权平均来计算保险业指数,以此衡量保险业的整体市场状况。本文的保险机构数据来源于Wind数据库,以新华保险较晚交易时间为基期时间,样本期为2011年12月16日至2022年1月28日,样本量为2461个,主要使用S-Plus和Matlab软件工具进行数据分析。保险机构和保险业指数收益率序列的计算公式如下:
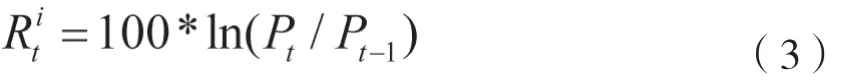

本文根据AIC准则确定保险机构和保险业收益率序列的最优边际分布模型,具体而言,均值模型形式为ARFIMA(1,0,0),方差模型形式为GJR(1,1),残差分布模型形式为有偏学生 分布,即AR(1)-GJR(1,1)-有偏模型能够较好地处理各个收益率序列中的自回归、波动聚集和杠杆效应问题。GJR模型的参数估计和拟合结果如下:
表1主要包括参数估计和模型拟合效果检验两个部分。具体而言,根据ARCH项参数可知,中国人寿对市场信息的反应最为敏感,其次为中国平安和中国太保,新华保险的反应最为迟缓。根据GARCH项参数可知,中国平安和中国太保对市场波动有较强的记忆性,而中国人寿和新华保险的记忆性较弱。根据非对称项系数的正负方向可知,各个保险机构和保险业在面对外部信息冲击时存在非对称效应,新华保险受到利空消息的影响更大,而中国人寿、中国平安、中国太保和保险业更容易受利好消息的影响。根据尺度参数和形状参数可知,各个保险机构和保险业的残差序列分布具有非对称性和厚尾性特征。根据LB检验可知,各个保险机构和保险业的残差序列不存在自相关,根据ARCH检验可知,各个保险机构和保险业的残差序列不存在ARCH效应,表明GJR模型已消除其条件异方差。

表1 边际分布模型的参数估计和拟合结果
在确定边际分布模型之后,提取各个保险机构和保险业的标准残差序列,通过概率积分变换为均匀分布形式的数据,以此构建Copula模型,进而计算相依系数。基于Copula模型的相依结构关键在于最优Copula的选取,本文选择Gaussian Copula、Student's t Copula、Gumbel Copula、Frank Copula、Clayton Copula和SJC Copula等常用Copula函数,使用LogLike、AIC和BIC准则来确定最优Copula,在既定的最优Copula函数和参数估计下,进而可以计算各个保险机构和保险业之间的Kendall相关系数、Spearman相关系数和尾部相关系数。
根据表2可知,存在如下特征:(1) 根据最优Copula可知,各个保险机构和保险业连接的最优Copula函数均为SJC Copula,该函数具有非线性、非对称性和厚尾性等特征;(2) 根据上尾相关系数和下尾相关系数可知,各个保险机构和保险业之间的下尾相关系数均大于上尾相关系数,如中国人寿和保险业的上尾相关系数为0.4460,下尾相关系数为0.5947,表明相对于利好消息,中国人寿和保险业对利空消息更为敏感;(3) 根据Kendall相关系数和Spearman相关系数可知,各个保险机构和保险业之间存在较强的正向相依关系,表明当保险机构或者保险业发生风险时,通过相关的风险传导和溢出机制,则保险业或者保险机构也会面临相关风险的概率,这对政策的启示在于“太关联而不能倒”;(4) 中国人寿和保险业的相依程度最大,反映中国人寿在保险业的主导地位,其次为中国太保和保险业、中国平安和保险业,相依程度最弱的是新华保险和保险业,这对政策的启示在于“太大而不能倒”。

表2 保险机构和保险业的相依结构
风险相依度是一种互相关性,而风险溢出具有明确的方向性。本文基于边际分布模型AR(1)-GJR(1,1)-有偏 模型,使用DCC-CoVaR模型,测度各个保险机构对保险业的动态风险溢出效应,对我国上市保险机构的系统重要性进行评估。图1从左至右、从上至下分别为中国人寿、中国平安、中国太保和新华保险对保险业的动态风险溢出效应。存在如下特征:(1) 从绝对值来看,各个保险机构对保险业的均值风险溢出效应分别为2.8335、2.5573、2.8052和2.4259,表明中国人寿对保险业的风险溢出效应最大,其次为中国太保对保险业、中国平安对保险业,而新华保险对保险业的风险溢出效应最小。总体而言,由于中国人寿的保险业务广泛、营业收入多、规模大以及与其他保险机构业务往来密切,因此中国人寿一旦发生风险和危机,将迅速传染至其他的保险机构,进而对整个保险行业产生相对应的风险影响;(2) 从相对变化趋势来看,各个保险机构对保险业的动态风险溢出效应的趋势基本一致,在2015-2016年的时间区间内,各个保险机构对保险业的风险溢出效应较大,且波动程度较大,这主要是由于股票市场的剧烈波动带来的风险影响到各个保险机构的收益和投资决策,导致各个保险机构的风险急剧增加,这表明保险机构除了要防范自身风险外,还要抵御来自资本市场和宏观经济的风险波动和危机传染。

图1 各个保险机构对保险业的动态风险溢出效应时序图
四、结论与政策建议
本文基于AR(1)-GJR(1,1)-有偏 模型,对中国人寿、中国平安、中国太保、新华保险和保险业收益率序列的边际分布进行了拟合,使用GJRSJC-Copula模型来分析了4家保险机构和保险业之间的风险相依关系,使用DCC-CoVaR模型测度了4家保险机构对保险业的动态风险溢出效应。结果表明:第一,各个保险机构和保险业之间具有较强的风险相依度,且存在下尾相关的非对称效应,更容易受到利空消息的冲击和影响,下跌的可能性大于上行的可能性;第二,对于风险溢出效应而言,中国人寿对保险业的风险溢出效应是最大的,变化波动程度也是最为显著的,其次为中国太保和保险业、中国平安和保险业,而新华保险对保险业的风险溢出值最小;第三,在动态风险溢出效应的变化趋势中,容易受到某个危机或者极端事件的影响,当危机或者风险事件出现时,各个保险机构对保险业的风险溢出效应均会有显著的增加。为了加强对保险机构的风险防控,本文提出以下建议:
第一,完善保险机构的风险防控和监管体系,健全重大风险应急机制。从系统性风险的角度来看,要提高对保险机构的监管要求,加强在非保险业务方面的审批和监管,完善保险机构的信息披露,坚持宏观审慎监管和微观审慎监管相结合的监管理念,以避免保险机构在规模和业务等方面的盲目扩张而发生重大风险隐患,降低风险外溢能力和水平。同时,极端事件的爆发对保险机构的风险具有较大的影响,因此要通过设置系统的风险预警和评估机制,对保险机构在系统性金融风险方面进行科学的识别和预测,制定系统和有效的重大风险应急机制,以确保保险机构在发生重大风险时能够得到快速、安全和有效的应对处置。
第二,健全财政在保险机构危机救助的机制。财政的危机救助有利于恢复保险市场秩序,稳定风险预期,提升保险机构的市场竞争力。一方面,要明确财政救助在系统性风险中的基本职能和监管责任,做到财政救助的有度和有效,不能盲目的财政救助和行政干预,防止出现“太大而不能倒”的道德风险,让保险机构的业务经营和风险管理均处于健康发展和良好循环之中。另一方面,在确定对保险机构进行财政救助后,通过减免税收优惠政策、设立专项救助资金、发行政府债券、提供信用担保和实现国有化等多种渠道和措施,对保险机构在发生金融风险时进行及时和有效的危机救助。
第三,加强监管合作,提高监管效率。保险机构之间具有一定的关联性,存在“太关联而不能倒”,在保险机构处理自身风险的同时,还要防止其他保险机构的风险传导和影响。因此保险机构之间要加强风险监管方面的合作,在保障保险机构之间业务合作的同时,还要降低保险机构之间风险传染和共振。同时,从政府相关监管机构的角度来看,近年来保险机构的业务开展逐渐多元化,其风险存在发生频率高、风险损失大和风险关联隐蔽复杂等特征,对保险业形成风险冲击,因此需要各个政府监管部门之间加强监管合作,注重风险监管工作的协调性。

