基于聚类共晶团算法的蠕墨铸铁形核率预测模型

姜爱龙，李娜娜，刘庆义，王 健，宋 琳，王迎光，田学雷

(1.内燃机可靠性国家重点实验室(潍柴动力股份有限公司)，山东 潍坊 261061；2.材料液固结构演变与加工教育部重点实验室(山东大学 材料科学与工程学院)，济南 250061)

蠕墨铸铁是石墨形态介于片状石墨和球状石墨之间的一种过渡形态的铸铁，因其石墨形状扭曲弯折，酷似蠕虫，故称为蠕墨铸铁。在基体组织相同的情况下，蠕墨铸铁的力学性能介于灰铸铁和球墨铸铁之间，且具有良好的导热性和较小的断面敏感性，因此作为一种新型工程结构材料被广泛使用。蠕墨铸铁早在1948年就被美国人发现，但作为工程材料开展的系统研究与应用是从上个世纪60年代才开始的[1]。据不完整统计，截至2012年，我国蠕墨铸铁的年产量为50万吨，且仍呈现连续增长的趋势[2]。

蠕墨铸铁具有球墨铸铁的高强度和耐磨性，且有类似灰铸铁良好的铸造工艺性、导热性、减震性，以及比灰铸铁高得多的疲劳强度和耐热疲劳性，它可在同等壁厚条件下保持高强度，从而实现铸件轻量化[3-4]。随着汽车产业的发展，对汽车轻量化的要求也越来越高，而蠕墨铸铁比灰铸铁和铝合金的抗拉强度高出75%以上，弹性模量高40%以上，疲劳强度高出近100%，且其具有高温稳定性，因此，它是当前及未来发动机缸体缸盖设计制造的理想材料[5]。

通常，铸造凝固过程的形核率对于铸件的综合性能具有重要的影响。这主要体现在，形核率会直接影响凝固过程的冷却曲线，同时会决定铸造产品的微观结构及力学性能[6-7]。因此，形核率是铸件凝固过程仿真计算和铸件性能预测的重要参数指标。相较于灰铸铁和球墨铸铁，蠕墨铸铁的凝固具有其独特之处。首先，由于蠕墨铸铁的最大过冷度要大于球墨铸铁和灰铸铁，即蠕墨铸铁铸件在凝固前需要过冷至共晶线以下更低的温度，导致其凝固过程中会出现大量的奥氏体枝晶，使得蠕墨铸铁的凝固组织由奥氏体枝晶和各种形态的石墨形成的共晶团组成[8-10]。研究显示[11-12]，蠕墨铸铁的奥氏体枝晶与石墨的形核和生长在熔体中独立进行，石墨颗粒最初在熔体中生长，逐渐与同样生长着的奥氏体枝晶接触，形成共晶团。在该共晶团中，奥氏体和石墨共同生长，两相均与熔体接触。当铸件处于较高冷却速率的部分达到较大的过冷度时，会出现较大的奥氏体形核密度，从而导致晶粒尺寸较小。另一方面，较慢的冷却部分奥氏体形核密度较低，因此具有较大的晶粒尺寸。这些晶粒中每一个都包含许多球状共晶团[13]。由于蠕墨铸铁特殊的形核生长模式，若直接使用石墨个数来取代共晶团数，会使得到的形核率数据在用于仿真计算时，出现较大的计算误差，同时，由于蠕墨铸铁中石墨取向一致性较弱，应用于灰铸铁试样的共晶团统计方法也难以直接被应用到分析蠕墨铸铁试样上。

为了解决上述问题，本文拟采用凝固模拟的方法，基于聚类算法的方式建立一种全新的描述蠕墨铸铁共晶凝固过程的形核率预测模型及对应的生长模型。同时，用统计金相照片中的石墨个数得到形核率的方法作为对照，然后将两种模型计算后得到的冷却曲线和蠕化率与实验结果进行直接对比来验证模型的合理性。最终，实现用凝固模拟的方式准确预测蠕墨铸铁的形核率，从而达到指导实际生产和节能环保的目的。

1 研究方法

1.1 实验方法

本文所用的实验数据均来自潍柴集团所生产的蠕墨铸铁缸体。该缸体通过HWS静压造型生产线生产，铸型材料为湿型砂。使用LWD200-4XC型金相分析仪获取蠕墨铸铁样品的金相照片。在每一个蠕墨铸铁样品表面刻画9个网格，然后在每一个网格内通过金相分析仪观测，以避免因蠕墨铸铁石墨分布不规律以及金相照片的局限性所带来的误差。

1.2 形核率模拟模型

本文所建立的模型是基于本课题组自主研发的铸造模拟软件TMcast(软件著作权编号2021SR0285281和2021SR0285282)所进行的二次开发，所需程序模块的数值模型主要包括凝固传热、边界条件设置以及潜热计算等基本模型，其具体原理为迭代求解三维非稳态差分温度场方程。

Δf=2aT·Δt

(1)

式中:Δf为单个时间步长内的固相率变化；2aT为温度场在三维实空间中的拉普拉斯算子，其中a代表对应方向上的热阻系数；Δt为单个时间步长的时间长度。

本文主要研究蠕墨铸铁的共晶凝固，因此仅详细介绍了共晶固相率模型。对于共晶凝固，被大家普遍认同的固相率计算公式为Johnson-Mehl公式[12]

(2)

式中:fs为固相率;R为共晶团半径;N为单位体积内共晶团数量，即形核率。该公式考虑了共晶团生长后期互相接触碰撞的影响并进行了修正。从式(1)可以看出，如果能够得到共晶团半径随时间变化的规律R(t)和形核率随时间变化的规律N(t)，就能够得到蠕墨铸铁共晶凝固过程中的固相率变化，因此需要建立形核模型和生长模型来完成计算。

铸造凝固过程的形核阶段十分复杂，但为了方便建模，通常将形核模型简化为两种模型：瞬时形核模型和连续形核模型。本文采用更能反应实际结果的瞬时形核模型来计算形核率[13-14]，该模型可表示为

(3)

式中：NS为单位面积内的形核数；K3和K4为常数，可通过实验直接获得。单位体积内的形核数为

(4)

对于蠕墨铸铁的共晶生长过程，可以采用Oldfield提出的生长模型理论，

(5)

该公式在各种铸铁共晶生长模拟中被广泛采用。式中：R为共晶团半径；B为生长系数；ΔT为过冷度。为了把固相率场的计算转化成程序语言，需要将上述形核和生长公式进行离散化处理。首先，将形核公式差分化，可得

(6)

式中：Told和Ttemp分别表示上一步的温度场和温度的暂存场；Δt为差分时间步长。然后，将生长公式差分化，可得

Rtemp=B·ΔT2·Δt+Rold

(7)

式中：Rtemp为共晶团半径暂存场；Rold为旧共晶团半径场。最终根据固相率计算的Johnson-Mehl公式可得到当前的固相率为

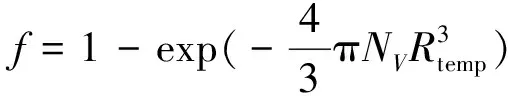
(8)

固相率fs的取值范围为0～1，当fs=1时固相率计算停止。固相率改变场通过当前步长计算的固相率与上一步计算的固相率(fold)作差获取，即

Δf=f-fold

(9)

2 结果与讨论

蠕墨铸铁的共晶团是由石墨与奥氏体共生生长形成的，共晶团在生长过程中，奥氏体生长的更快，常常将石墨包围起来，这就使得蠕墨铸铁共晶团中，石墨之间的连通率要小于灰铸铁共晶团中的石墨连通率，且由于蠕虫状石墨端部呈半圆形，每个共晶团之间石墨端部互不连通，有一定的间隙。而在共晶团内部，石墨之间的距离较近，且常有分枝联通。依据以上的理论和观察到的现象，可以认为两个蠕墨铸铁共晶团边界上石墨的距离要大于共晶团内部石墨的距离，在金相图上表现为存在着石墨相互聚集的石墨丛，石墨丛之间有明显的分界线。

为了合理地统计这类共晶团，本文采用DBSCAN聚类算法对石墨进行聚类，DBSCAN(Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法)是一种基于密度的空间聚类算法。它利用基于数字图像处理的聚类算法以距离为判断依据对石墨进行聚类，可以认为得到的聚类数与共晶团数成正比关系，因此，可以用聚类数代替共晶团数进行形核率计算。该方法不需要输入聚类数，因此可排除人为的干扰，使统计的数据客观且更具说服力。不仅如此，考虑到金相照片显示的随机性，过滤噪声点同样很重要。

根据经典的形核生长理论，随着过冷度的增加，共晶团的数量会呈指数级别上升，一个共晶团内部又存在着许多的石墨。因此，可以认为随着共晶团数量的增加，石墨的数量也会增加。因此，可以假定从金相照片上统计到的石墨个数正比于共晶团数，可以采用石墨个数代替共晶团数建立形核模型[15-16]。

通过碳硫分析仪和Spectro GENESIS直读光谱仪测得蠕墨铸铁缸体化学成分，如表1所示。

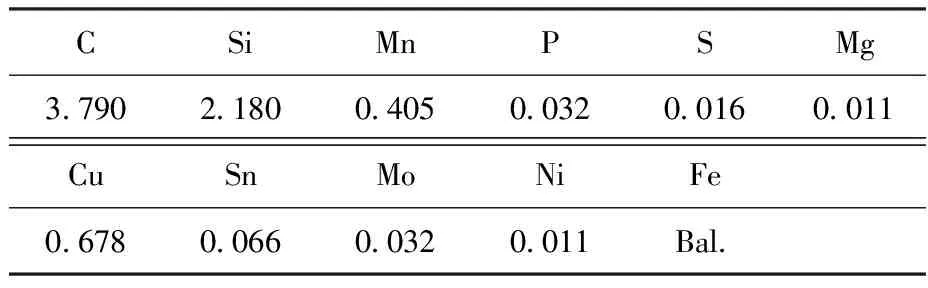
表1 蠕墨铸铁化学成分(质量分数/%)

经计算碳当量为4.5，王继俭[17]的研究显示，当碳当量在4.37%～4.55%时，蠕墨铸铁以近共晶模式凝固。

2.1 DBSCAN聚类算法的共晶团统计

使用DBSCAN聚类算法需要3个参数，分别是数据集、指定半径ε以及密度阈值minPts。数据集是指以点的坐标为基本单位的集合，因此，想要对金相照片中的石墨进行聚类处理，首先需要提取一张图片上所有石墨的质心坐标，用质心坐标代替石墨进行聚类统计。该算法的实施主要需要两个步骤。

第1步是提取数据集。首先，通过MATLAB实现将金相图片转换为数据集的操作，通过imread函数载入图像，然后通过im2bw函数将图片转换为二值图，并对转换后的二值图采用medfilt2函数进行滤波，用bwareaopen函数去除500个像素以下的噪声点，用strel函数进行膨胀腐蚀去除内部空洞，处理好的图像与未处理的图像对比如图1(a)和(b)所示。随后，采用bwboundaries函数识别并显示图像目标中的边界，然后采用bwlabel函数对图像中的连续区域进行标记并进行伪色彩化，处理后的金相照片如图1(c)和(d)所示。

图1 金相照片处理步骤演示:(a)未处理的金相照片;(b)处理后的金相照片;(c)边界标记后的图像;(d)伪色彩化并标记后的图像

在得到图1(d)所示的图像后，采用regionprops函数对图像中的每个目标提取二值特征，其中包含图像目标的质心坐标，因为函数原因，该坐标与实际位置呈180°关系。将质心坐标按散点图绘制后如图2(a)所示，通过对每一个金相照片进行这样的操作，便得到了一系列的数据。

第2步是DBSCAN算法统计。该算法需要的3个参数中的数据集已经获取，另外两个参数ε以及minPts需要进行指定。由于样品的冷速不同，随着冷速的增大，共晶团半径变小，共晶团内部的石墨距离变短，石墨更加密集，且共晶团之间的距离变短。在这种条件下，应指定ε随着冷速的减小而减小，以保证与实际情况相符合，表2为各样品ε以及minPts的设置数值。3个参数设定好后，将参数传入DBSCAN算法中，图2(b)显示了聚类后的效果。如图2(b)显示，经过聚类后将原来的石墨分成了两类，并将噪声点排除。但由于金相图片的随机性，导致部分金相图片聚类效果较差，因此，设定规则为：当存在大面积的噪声点时，该数据不计入平均聚类数中；当一类中点的个数小于5时，该类不计数。对9个样品的81张金相照片进行聚类后获取每个金相照片上的聚类数，并对一个样品内的金相照片的聚类数求平均，得到了9个样品的平均聚类数，采用该数来代替形核数进行形核公式的确定。统计后得到的各样品的平均聚类数如表3所示。

表3 各样品的平均聚类数

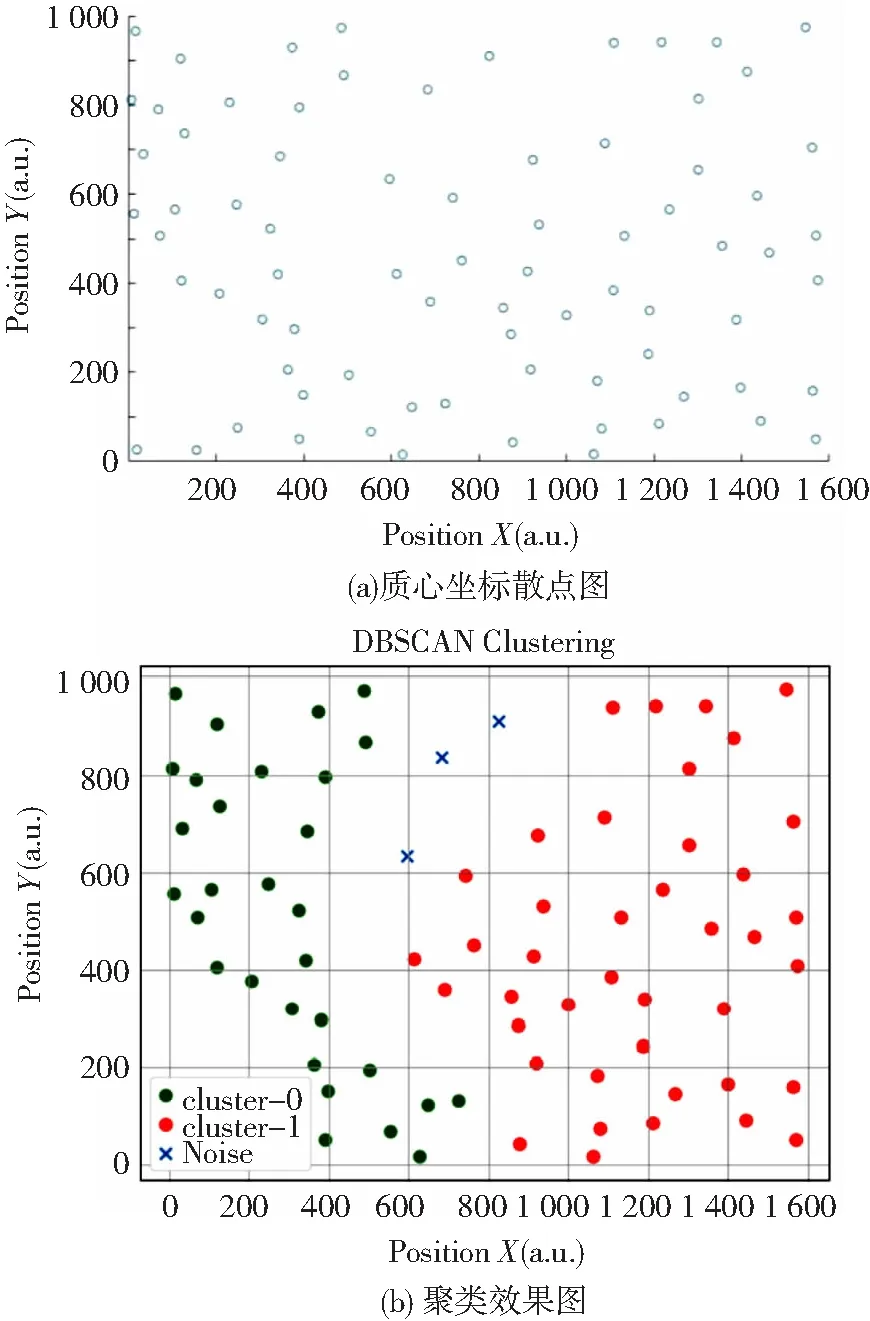
图2 数据处理可视化

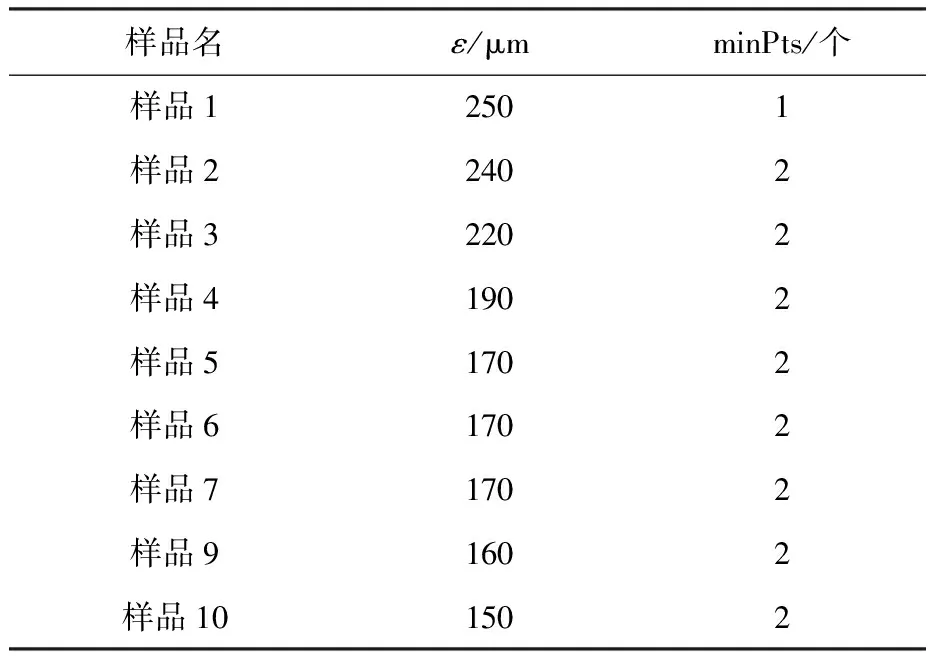
表2 各样品半径ε以及密度阈值minPts的设置数值

后续，统计了金相照片中石墨个数、石墨面积以及石墨最大中心线长度等信息，为随后建立石墨形状参数模型做准备。其中，一个样品选取了9张金相照片，对每个金相图片进行石墨个数统计后取其平均值，用平均石墨个数代替共晶团数来确定形核公式。统计得到的各样本平均石墨个数的数据如表4所示。

表4 各样品的平均石墨个数

2.2 形核和生长模型的建立

假设瞬时形核，且所有的核心均在共晶反应开始前的最低温度Tm析出，即Tm点为共晶形核温度TN，则共晶形核温度与冷却速率的关系可由下式计算得出。

ΔTm=A·(RE)n

(9)

TN=TE-ΔTm

(10)

式中A,n为经验参数，通过实验确定。通过对所测得的冷却曲线分析可得最大过冷度(ΔTm)和共晶温度时的冷却速度(RE)的数据，如表5所示。

表5 冷却曲线得到的最大过冷度ΔTm与冷却速度RE

通过MATLAB对表5数据拟合可得到最大过冷度ΔTm与共晶温度时冷却速率RE的关系为

(11)

该拟合方程的确定系数(R2)为0.960 7，拟合曲线如图3(a)所示。要获得形核公式，还需要将上文中获得的平均聚类数和平均石墨个数除以金相照片的面积，获得每平方米内的平均聚类数和平均石墨个数。经测量金相照片的面积为0.245 mm2。

图3 不同变量以共晶温度为自变量的拟合曲线:(a)最大过冷度与共晶温度时冷却速率的拟合曲线;(b)平均聚类数与共晶温度时冷却速度的拟合曲线;(c)平均石墨个数与共晶温度时冷却速度的拟合曲线;(d)蠕化率与共晶阶段冷却速度的拟合曲线

2.2.1 聚类数代替共晶团数的形核公式

将表3所示的聚类数目用式(2)通过MATLAB进行拟合后得到形核公式

NS=6 680 000+87 190(RE)2

(12)

其中，NS为单位面积内的聚类数，个/m2。该拟合方程的确定系数R2为0.6835，拟合曲线如图3(b)所示。单位体积内共晶团的数量可由式(3)计算。

2.2.2 石墨个数代替共晶团数的形核公式

将表4所示的平均石墨个数通过MATLAB进行拟合后得到形核公式,

NS=257 000 000+1 603 000(RE)2

(13)

该拟合方程的确定系数R2为0.273 6，拟合曲线如图3(c)所示。

由于两种形核公式计算得到的形核数存在数量级上的差别，因此，对于不同的形核公式应采用不同的生长公式，以获得正确的固相率计算情况。

2.2.3 聚类数代替共晶团数的形核公式的生长公式

对于蠕墨铸铁的共晶凝固，只需考虑共晶凝固情况下的生长，采用式(4)作为生长模型，经试算生长系数B取9.693×10-4m/(s·K2)。生长公式如式(14)所示。

(14)

2.2.4 石墨个数代替共晶团数的形核公式的生长公式

与上面的方法相似，采用式(4)作为生长模型，经试算生长系数B取9.208×10-5m/(s·K2)。生长公式如式(15)所示。

(15)

对于统计好的金相图片中的石墨面积和石墨最大中心线长度，将圆形系数<0.525的石墨统计为蠕虫状石墨，圆形系数在0.525～0.625的统计为团絮状石墨。统计蠕虫状石墨的总面积、团絮状石墨的总面积以及所有石墨颗粒的总面积，则蠕化率可按式(16)计算。

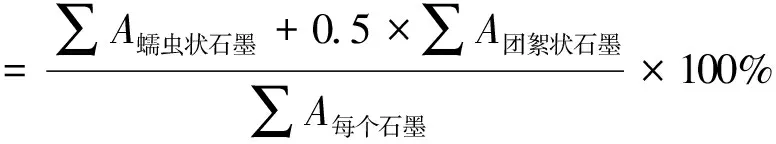
(16)

式中：A蠕虫状石墨代表蠕虫状石墨颗粒的面积；A团絮状石墨是团絮状石墨颗粒的面积；A每个石墨对应每个石墨颗粒的面积。

以往研究表明，同一化学成分、同一铸造条件下蠕墨铸铁的蠕化率与共晶温度时冷却速度有关，二者存在二次函数关系[18]，因此本文也采用该函数关系确立石墨形状参数模型。各样品蠕化率和各样品共晶温度时冷却速度如表6所示。

通过MATLAB对表6数据拟合可得

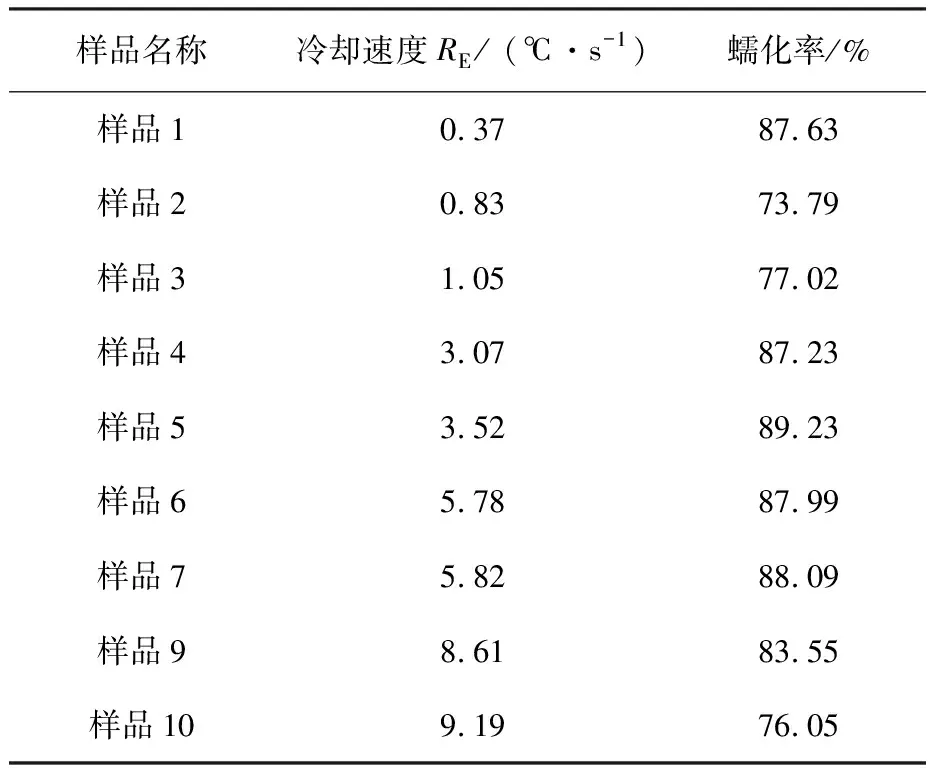
表6 各样品蠕化率和各样品共晶温度时冷却速度

(17)

该公式的确定性系数R2为0.929 6，拟合函数图像如图3(d)所示。蠕化率是石墨形状参数的综合体现，因此，可以认为蠕化率模型即为石墨形状参数模型，蠕化率随着共晶阶段冷却速度的变化规律对工艺调整具有重要意义。

2.3 冷却曲线与实验验证

为了验证所建立的形核率预测模型的合理性，本文设计浇注了6，12，18，25，35，45 mm的6个长方体铸件，并通过热电偶进行测温，以1 s为采样间隔连续测量冷却曲线，将测得的实验冷却曲线用于对比分析两种算法得到的形核率与实际情况的符合程度。同时，使用自研的TMCast软件分别以石墨数统计出的形核率和聚类共晶团统计出的形核率作为初始条件进行凝固仿真。铸件三维形貌和形核率模型的实现平台TMCast软件的操作界面，如图4所示。

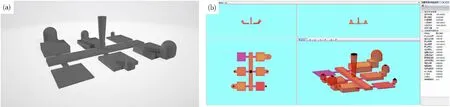
图4 软件界面展示实验铸件三维图(a)及TMCast程序界面(b)

图5绘制了不同尺寸的试样，使用两种不同形核模型进行仿真模拟的温度曲线，以及实验温度曲线，可以清晰地看到，聚类共晶团统计的形核率对凝固仿真的准确性具有重要影响。

由图5可以看到，在共晶平台出现位置和持续时间的预测上，使用聚类数计算共晶团数目得到的形核率，与实验结果更为符合。同时可以看出，在壁厚较小的6和12 mm试样中，使用石墨数计算共晶团数目得到的形核率，在一定程度上会让总冷却时间的模拟计算结果更贴近实际，这是由于获取绝热涂料层导热参数难度较高，建模时需要将铸件与铸型之间的接触视作理想接触，这会使得理论散热增加从而缩短冷却时间。由于使用石墨数计算形核率时，模拟凝固时共晶平台有后移和延长的趋势，反而弥补了这部分过高的导热导致的冷却时间缩短。

图5 使用石墨数代替共晶团数、采用聚类数代替共晶团数的形核公式的模拟曲线以及实验测得的(a)6 mm、(b)12 mm、(c)18 mm、(d)25 mm、(e)35 mm、(f)45 mm冷却曲线对比图

而在壁厚较大的试样中，此情况未发生的原因是，本文工作中所使用的传热模型未考虑对流导热的影响，而铸件较厚时不考虑对流导热导致的散热减少则会让总的理论冷却时间变长，通过观察进入共晶平台前的冷却曲线很容易发现这一点，这在一定程度上与不考虑界面热阻导致的冷却时间变短相互抵消。在本文工作中，由于模拟计算模型进行了一定的简化，总冷却时间参考价值不高，但是共晶平台的形状和位置则较大程度上说明了本文算法的合理性。

在TMcast程序计算出温度场后，依据不同位置的冷却速度与石墨形状参数计算出试件各部分的蠕化率情况，表7显示了程序对6，12，18，25，35，45 mm的6个长方体铸件的蠕化率模拟预测情况。

表7 蠕化率模拟预测结果

3 结 论

本文采用DBSCAN聚类算法分析金相照片得出共晶团统计数量，并使用新的共晶团统计数量作为形核率，建立了冷却速度与形核率之间的关系，通过凝固模拟结果得知，冷却曲线和共晶团形核率的预测均与实验结果吻合很好，可用于预测蠕化率。

实验和凝固仿真计算结果表明，蠕墨铸铁蠕虫状石墨的形核生长为共晶团生长模式，若要对凝固过程进行介观层面的仿真，使用共晶团生长模型会更加符合实际情况。