基于TCN-LSTM和气象相似日集的电网短期负荷预测方法

刘 辉，凌宁青，罗志强，孙志媛

（1.广西大学电气工程学院，广西南宁 530004；2.广西电网有限责任公司电力科学研究院，广西南宁 530023）

0 引言

在大量分布式能源以及电动汽车等主动负荷因素的影响下，电网需求侧呈现众多不确定性，电网安全运行面临严峻挑战[1]。短期负荷预测是电网安全运行的关键环节。相似日选取是电网短期负荷预测的关键步骤[2]，实际上是对预测模型的输入特征进行选择[3]，充分挖掘相似日中蕴含的关键信息，是提升电网短期负荷预测精度的有效方式。

气象因素对负荷变化的影响明显[4]，因此通过气象因素选取相似日可较好地反映负荷的相似性。文献[5-6]通过考虑日特征气象等因素选取相似日，但日特征气象属于粗粒度数据，难以反映气象1 d 内的变化，存在整体相似而局部不相似的情况，影响相似日选取。随着计量仪器的进步，气象监测部门已能提前获知未来日期的实时气象数据，利用实时气象数据选取相似日，能更好地反映每日气象的变化规律[7]。文献[7-8]将各实时气象组合成混合气象序列选取相似日，会造成选取相似日时的特征冗余，计算结果会受其他气象因素影响，相似系数被“平均化”，影响相似日选取结果，且不同气象因素对应的相似日可能不同，不利于预测模型挖掘不同气象因素的相似日信息。

人工智能方法具有较强的非线性数据拟合能力，是目前短期负荷预测的常用方法[9]。人工智能方法包括支持向量回归（Support Vector Regression，SVR）[10]、卷积神经网络（Convolutional Neural Networks，CNN）[11]、时间卷积网络（Temporal Convolutional Network，TCN）[12]、长短期记忆（Long Short-term Memory，LSTM）网络[13]等。SVR 不能很好地考虑数据的时序特性，导致预测精度往往不够理想。CNN 可通过卷积核的卷积操作实现特征映射，提取输入特征的信息，实现特征融合[14]，TCN 是针对时序问题在CNN基础上的改进，具有扩张因果卷积结构，能提取间隔较长和非连续时序数据的特征信息[15]，在时序预测问题上特征提取的优势明显。LSTM 网络是一种专门处理时序问题的循环网络，能有效学习时间序列的长期依赖关系[16]，在负荷预测中取得了良好的效果。

因此，本文提出一种基于TCN-LSTM 和气象相似日集的电网短期负荷预测方法。从线性与非线性角度，用Pearson 系数和最大信息系数（Maximal Information Coefficient，MIC）分析负荷和气象因素的相关性，选出与负荷相关性强的气象因素；基于形态相似距离方法选取该气象因素对应的最佳相似日组成气象相似日集，以气象相似日集负荷、历史负荷、气象因素、时间因素作为预测模型的输入特征；搭建TCN-LSTM 预测模型，通过中国某地区的实际历史数据验证所提方法的有效性。

1 气象相似日集选取

1.1 相关性分析方法及原理

1.1.1 线性相关性分析

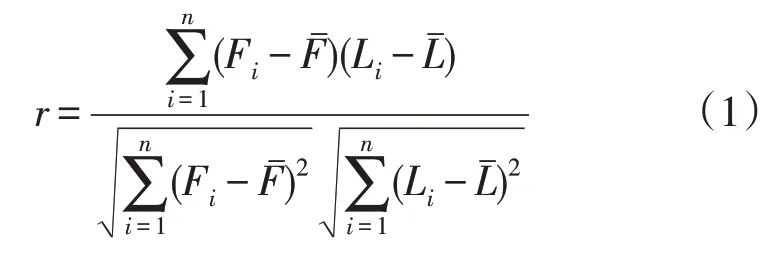
Pearson 相关系数是分析不同变量间线性相关性的常用方法，其计算公式为：式中：r为变量间的Pearson 相关系数；为变量F的平均值；为变量L的平均值；n为数据样本大小。

当 |r|越大，说明相关性越强。通常而言[17]，当|r|≥0.6 表示强相关，|r|∈[0.4,0.6)表示中等程度相关，|r|∈[0.2,0.4)表示弱相关，|r|∈[0,0.2)表示极弱相关或无相关。

1.1.2 非线性相关性分析

MIC 可以衡量变量之间的非线性相关性。在一个数据集D中，沿数据集的坐标轴方向划分区间，得到x×y个网格，二元数据集在每个网格的概率分布D|G，I(D|G)代表D|G的互信息。数据集D每个网格的最大标准化互信息组成特征矩阵M（D），矩阵元素如式（2）所示[18]：

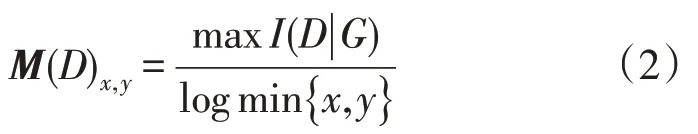
由此可计算MIC，如式（3）所示：

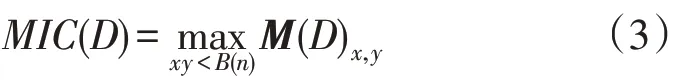
其中，x与y的乘积需小于B(n)，一般B(n)=n0.6。MIC 的度量标准一般是通过比较MIC 值的大小来反映变量间的相关性，MIC 值越大，说明2 个变量的相关性越强。

1.2 负荷与气象因素的相关性分析

为深入探究不同气象因素对负荷的影响程度，需要对负荷与气象因素进行相关性分析。因负荷在不同季节的变化规律不同，为全面衡量在不同季节气象因素对负荷的影响，分别采用Pearson 相关系数与MIC 分析各个季节负荷与气象因素的线性和非线性相关性。需要注意的是，由于本文收集到的气象数据分辨率为1 h，而负荷数据分辨率为15 min，为使气象数据与负荷数据相匹配，因而对气象数据进行线性插值，得到分辨率为15 min 的气象数据[19]。各季节的时间划分为春季3—5 月、夏季6—8 月、秋季9—11 月、冬季12—2 月[20]。选取中国某地区2011 年3 月至2012 年2 月的负荷和气象数据进行分析计算，主要考虑4 个气象因素：温度（摄氏度）、湿度（%）、降雨（mm/h）、风速（m/s）。F=[F1,F2,...,Fn]代表各个气象因素，L=[L1,L2,...,Ln] 代表负荷，其计算结果如表1 和表2 所示。

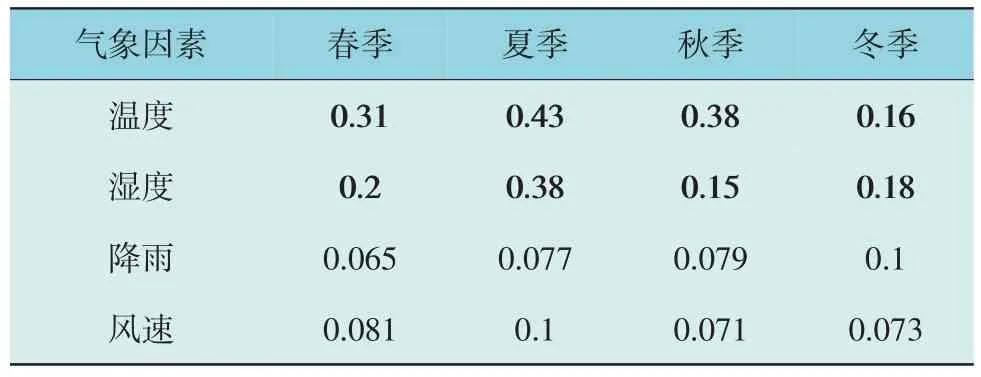
表2 负荷与气象因素的非线性相关结果Table 2 Nonlinear correlation analysis between load and meteorological factors

由表1 可知，在春季，温度和湿度的 |r|在[0.4-0.6]之间，说明负荷与温度存在中等程度相关。在夏季，温度和湿度的 |r|均大于0.6，说明与负荷存在强相关。在秋季，温度的 |r|大于0.6，说明负荷与温度存在强相关；湿度的 |r|处于[0.2-0.4）之间，与负荷存在弱相关，但明显大于降雨和风速的 |r|。在冬季，温度和湿度的 |r|在[0.2-0.4）之间，说明与负荷存在弱相关，但明显大于降雨和风速的 |r|。在四季，降雨和风速的 ||r均处在[0-0.2）之间，说明与负荷存在极弱相关或无相关。综合各个季节的分析结果，相对于降雨和风速，负荷与温度和湿度具有更强的线性相关性。

表1 负荷与气象因素的线性相关结果Table 1 Linear correlation analysis between load and meteorological factors

由表2 可知，在春、夏和秋季，温度和湿度的MIC 均远大于降雨和风速的MIC，说明相对于降雨和风速，负荷与温度和湿度的非线性相关性更强。在冬季，温度和湿度的MIC 虽比春、夏和秋季的MIC 小，但仍然大于降雨和风速的MIC，说明相对于降雨和风速，负荷与湿度的非线性相关性更强。综合各个季节的分析结果，相对于降雨和风速，负荷与温度和湿度具有更强的非线性相关性。

综上所述，根据线性和非线性的相关性分析结果，表明了负荷与温度和湿度具有更强的相关性。

1.3 气象相似日集选取

一般而言，日负荷曲线在工作日和休息日（周末和节假日）这2 种类型日差别较大。对同种类型日，在气象条件相似的日期，其负荷曲线和负荷大小也会有一定的相似性。因此，根据负荷与气象因素的相关性分析结果，由温度和湿度这2 个气象因素选取对应的最佳相似日，组成气象相似日集。如果温度和湿度选取的最佳相似日为同1 d，则取温度的第二相似日与最佳相似日组成气象相似日集。

形态相似距离是一种评估序列数据相似性的方法，它可从序列数据大小和序列数据形状2 个角度对序列数据的相似性进行评估[21]。故本文通过形态相似距离，选取待预测日的气象相似日集，其定义如下：

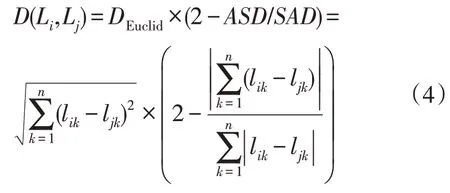
式中：Li为待预测日的实时气象序列；Lj为历史日的实时气象序列；lik为序列Li的第k个元素；ljk为序列Lj的第k个元素；DEuclid为2 个序列的欧式距离；ASD为2 个序列各数值差之和的绝对值；SAD为2 个序列的曼哈顿距离；D(Li,Lj)为2 个序列的形态相似距离，形态相似距离最小的历史日，即为最佳相似日。

考虑到“近大远小”原则，即负荷与历史时段中越近期的信息更相关[22]，因此在待预测日的前10 个同类型日的范围内进行相似日搜索。

2 TCN-LSTM预测模型

2.1 TCN原理

TCN 是在CNN 基础上的改进网络，具有独特的扩张因果卷积结构，更适用于解决时序问题。扩张卷积可对上一层的输入进行扩张采样，能提取间隔较长和非连续时序数据的特征信息。因果卷积可保证提取特征信息的因果性，t时刻的输出yt只能依赖于t时刻之前的输入x0～xt-1[23]。对于卷积核大小为2，扩张系数d分别为1，2，4 的TCN，其扩张因果卷积结构如图1 所示。计算公式参见文献[23]，受篇幅影响，此处不再赘述。

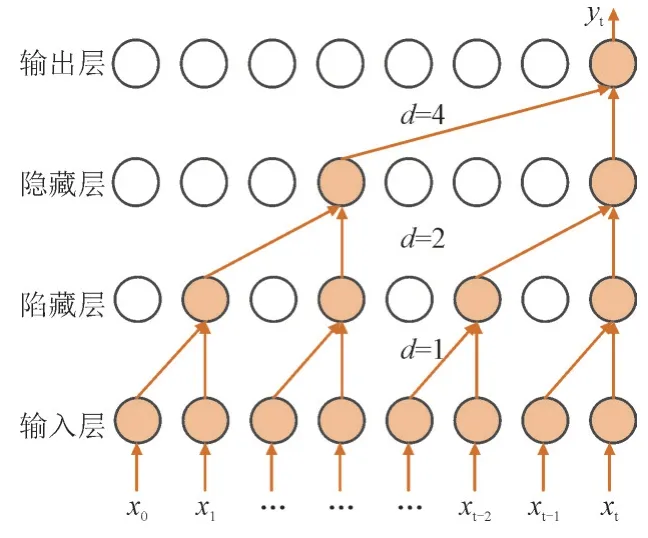
图1 TCN的扩张因果卷积结构Fig.1 Dilated causal convolution structure of TCN

2.2 LSTM网络原理

LSTM 网络是在循环神经网络基础上的改进网络，其记忆单元结构如图2 所示。其中，tanh 和σ为激活函数，xt和ht为当前记忆单元的输入和输出，Ct为当前细胞状态。

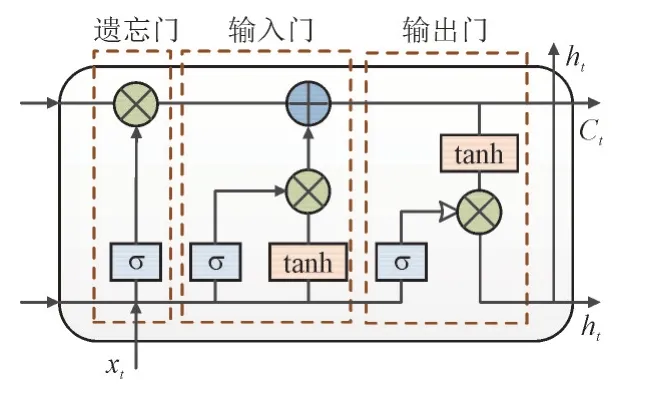
图2 LSTM的记忆单元结构Fig.2 Structure of LSTM memory unit

LSTM 网络在隐藏层单元中设计了遗忘门、输入门和输出门，并加入了存储信息的细胞状态功能，可学习时序数据中长时间尺度和短时间尺度的信息，有效缓解了训练时梯度消失的问题[24-25]。LSTM 网络各个门结构的计算公式参见文献[24]，受篇幅影响，此处不再赘述。

2.3 TCN-LSTM预测模型框架

由于TCN 具有扩张因果卷积结构，拥有突出的特征提取能力[26]，因此可对原始特征进行融合获得高维的抽象特征，加强了对特征信息的挖掘。而LSTM 网络具有强大的时序预测能力[27]，将TCN 和LSTM 网络结合，通过TCN 特征提取后输入至LSTM 网络，提高了LSTM 网络记忆单元的处理效率，使得预测模型更有效地学习时间序列的复杂交互关系。因此，本文搭建了TCN-LSTM 短期负荷预测模型，模型框架如图3 所示。

图3 TCN-LSTM预测模型框架Fig.3 TCN-LSTM forecasting model framework

图3 中，TCN 的层数为1，卷积核个数为32，卷积核大小为2，扩张系数d分别为1，2，4，其余参数为默认参数；LSTM 网络的层数为1，神经元个数为32，激活函数为relu。模型优化器选用Adam，学习率设为0.001，损失函数选用mae，迭代次数设为40次，batchsize 设为128。LSTM 网络后面接1 层全连接层，神经元数为1，代表1 个时刻的负荷预测值，连续预测96 个时刻的负荷值，从而得到1 d 的预测结果。

3 电网短期负荷预测建模

3.1 数据预处理

由于负荷和气象的数据量纲不同，为了避免数据不同量纲对模型训练的影响，用线性函数归一化方法将原始数据转换到[0，1]范围，如式（5）所示：

式中：xnor为归一化后的值；xo为待归一化的值；xmax和xmin分别为数据中的最大值和最小值。

得到模型的输出结果后，通过式（6）对输出结果进行反归一化处理，得到最终负荷预测值。

3.2 输入特征

本文预测模型的输入特征由以下4 部分组成（以待预测日的t时刻为例）。

1）考虑气象相似日的影响，选取待预测日对应的温度最佳相似日t时刻和湿度最佳相似日t时刻的负荷值作为气象相似日特征。

2）考虑到负荷曲线具有日周期特性和自回归特性，选取待预测日前3 天t时刻的负荷作为历史负荷特征。

3）考虑气象因素对负荷的影响，根据负荷与气象因素相关性分析结果，温度和湿度与负荷具有更强相关性。温湿指数THI可以体现温度和湿度两者的耦合作用，其定义参见文献[7]。因此，选取t时刻的温度、湿度和温湿指数作为气象特征。

4）考虑时间因素对负荷的影响，待预测日t时刻的负荷与季节类型SZ、类型日DM以及所处每天的时间点TN有关。SZ=，Z=[1,2,3,4]，其中1，2，3，4 分别代表春、夏、秋、冬4 个季节。DM=，M=[1,2]，1 为休息日，2 为工作日。TN=N=[1,2,...,96]，代表每天96 个时间点。因此，选取SZ，DM和TN作为时间特征。

本文预测模型的输入特征如表3 所示。

表3 本文预测模型的输入特征Table 3 The input features of the proposed method

为满足模型的数据输入要求，采用滑动时间窗对数据进行划分，其中时间步长设为32，数据输入形式如式（7）和式（8）所示：

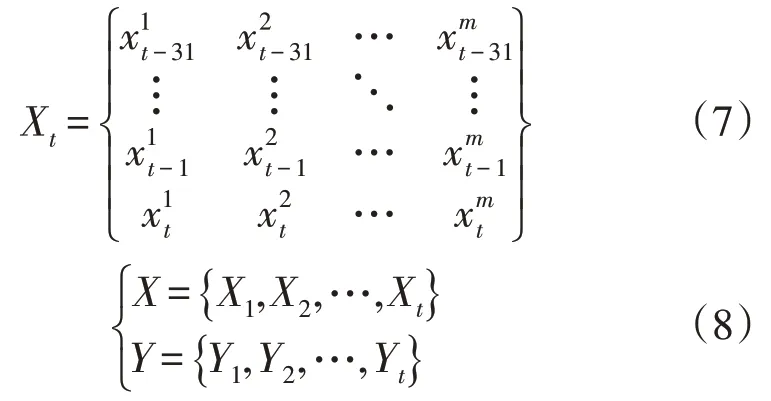
式中：Xt为第t时刻滑动时间窗的输入；m为输入的特征个数；X为预测时刻的输入；Y为预测时刻的输出。

3.3 电网短期负荷预测流程

本文方法的预测流程图如图4 所示，包含如下步骤：

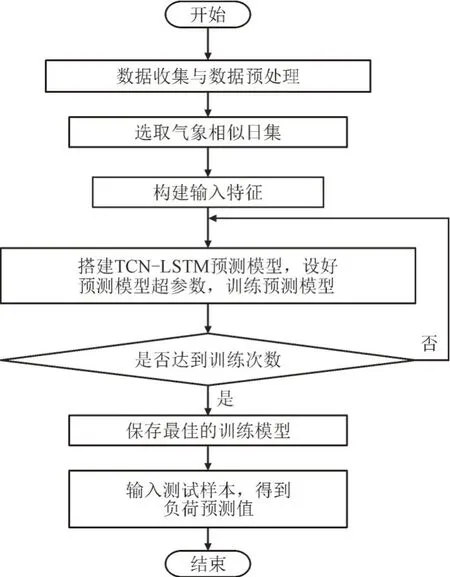
图4 本文方法的流程图Fig.4 Flowchart of the proposed method

1）数据收集与数据预处理。收集历史负荷和气象数据，对气象数据进行插值处理，对负荷和气象数据进行线性函数归一化处理，最后划分训练样本集和测试样本集。

2）选取气象相似日集。通过Pearson 系数和MIC 分析负荷与气象因素的线性和非线性相关性，选出相关性强的气象因素，并用形态相似距离选取各强相关性气象因素的最佳相似日，组成气象相似日集。

3）构建输入特征。取气象相似日集的负荷值，与历史负荷、气象因素和时间因素一同作为预测模型的输入特征。

4）模型训练。搭建TCN-LSTM 预测模型，设好模型各参数后，训练模型，并保存最佳训练模型。

5）模型预测。用测试集在最佳训练模型进行测试，对输出结果进行反归一化处理，得到负荷预测值。

4 算例分析

为验证本文所提方法的有效性，用中国某地区2010 年1 月31 日至2012 年12 月31 日的实际数据进行验证，数据的采样间隔为15 min，即每天采样96 个时间点。

4.1 实验配置和评价指标

本文实验配置是CPU 为Core i7-10700，内存为16 GB，操作系统为Windows 10 的计算机，基于Tensorflow 的keras 深度学习框架编写仿真程序。为了评估预测效果，选用平均绝对百分比误差（Mean Absolute Percent Error，MAPE）和平均绝对误差（Mean Absolute Error，MAE）对预测结果进行评价，其量值分别为EMAP和EMA。MAPE 和MAE 的值越小，表明预测效果越好。

4.2 气象相似日集选取

本文以2012 年8 月1 日为待预测日进行气象相似日选取，分别采用实时温度序列、实时湿度序列和混合气象序列选取对应的最佳相似日，对应的日期分别为2012 年7 月20 日、2012 年7 月19 日和2012 年7 月31 日，最佳相似日的负荷曲线如图5 所示。

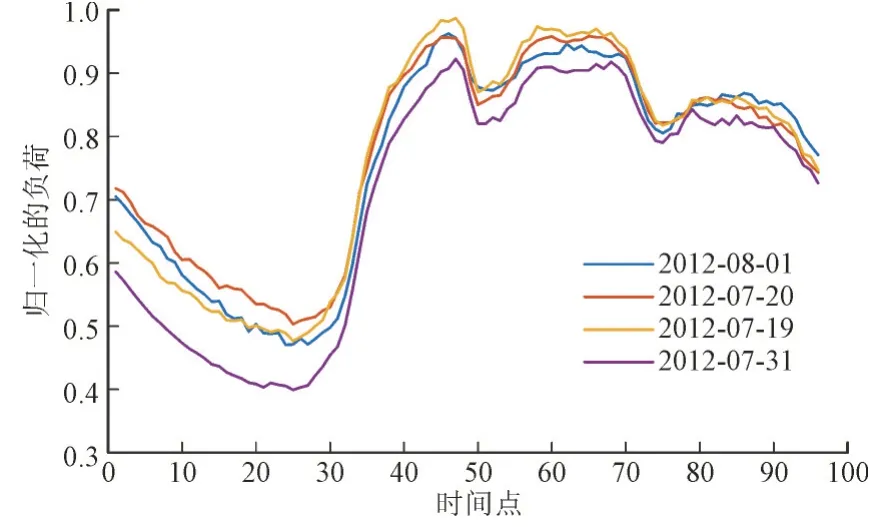
图5 最佳相似日的负荷曲线Fig.5 Load curve for optimum similarity day

由图5 可知，从负荷曲线形状上看，2012 年7月20 日的负荷曲线最贴近待预测日2012 年8 月1日的负荷曲线。进一步通过形态相似距离计算各最佳相似日负荷序列与待预测日负荷序列的距离值，评价选取结果，如表4 所示。

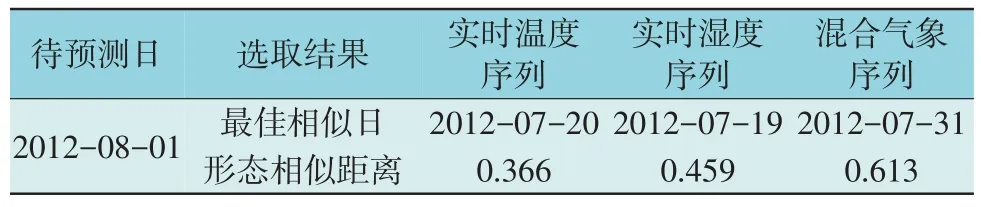
表4 最佳相似日比较Table 4 Comparisons of optimum similarity day

由表4 可知，与混合气象序列相比，由实时温度序列和实时湿度序列选取的最佳相似日的形态相似距离更小，选取的相似日更相似，说明相比于混合气象序列，用单一气象序列选取相似日能够避免其他气象因素的干扰，得到更好的相似日结果。

4.3 考虑气象相似日集的算例分析

对2012 年8 月1 日这1 天的负荷进行预测，选取2010 年1 月31 日至2012 年8 月1 日前1 天的数据作为训练集，选取训练集20%的数据作为测试集。为验证考虑气象相似日集在负荷预测中的优越性，与方法1 和方法2 进行对比分析。方法1的输入特征未考虑气象相似日特征，共9 个特征；方法2 的输入特征中的气象相似日特征，是由温度和湿度组成混合气象序列选取对应最佳相似日的负荷值，共10 个特征。预测结果如图6 所示。由图6 可知，本文方法的负荷预测曲线更贴近实际负荷曲线，说明本文方法的预测效果更理想。进一步计算MAPE 和MAE 指标，结果如表5 所示。

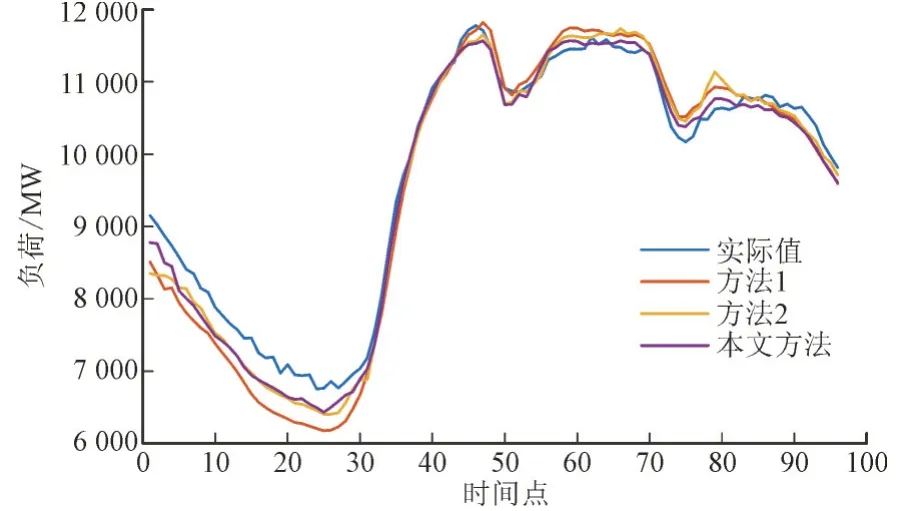
图6 不同方法的预测曲线Fig.6 Forecasting curve with different methods

表5 不同方法的预测结果Table 5 Forecasting results of different methods

由表5 可知，与方法1 相比，方法2 和本文方法的EMAP和EMA均更小，说明在输入特征中考虑气象相似日特征能提升负荷预测精度。与方法2 相比，本文方法的EMAP和EMA分别下降了0.41%和38.59 MW，说明考虑气象相似日集的影响在负荷预测中更具优势，能进一步提升负荷预测精度。

为进一步验证所提方法的普适性，对2012 全年进行日前负荷预测，选取2010 年1 月31 日至2011 年12 月31 日的数据作为训练集，选取训练集20%的数据作为测试集。预测结果如表6 所示。

表6 2012全年不同方法的预测结果Table 6 Forecasting results of different methods in 2012

由表6 可知，与方法1 和方法2 相比，本文方法的EMAP和EMA最小，表明在负荷预测中考虑气象相似日集作为输入特征能充分挖掘不同气象相似日的信息，可更好地体现不同气象相似日对负荷预测的影响，有利于提升负荷的预测精度。

4.4 不同模型的算例对比分析

为验证本文TCN-LSTM 预测模型的有效性，与不同预测模型进行对比。对比模型的参数设置如下：SVR 预测模型通过调用sklearn 包，参数均为默认参数；LSTM 网络预测模型的LSTM 隐藏层数为1，神经元个数为32；CNN-LSTM 预测模型由1 层卷积层、1 层池化层和1 层LSTM 层组成，卷积核个数为32，卷积核大小为2，池化层大小为2，LSTM 层神经元个数为32。用这4 个预测模型对2012 全年做日前负荷预测，选取2010 年1 月31 日至2011年12 月31 日的数据作为训练集，选取训练集20%的数据作为测试集。2012 全年不同模型的预测结果如表7 所示。

表7 2012全年不同模型的预测结果Table 7 Forecasting results of different models in 2012

由表7 可知，与SVR，LSTM，CNN-LSTM 预测模型相比，TCN-LSTM 预测模型的EMAP分别下降了2.13%，0.33%，0.21%，EMA分别下降了143.39 MW，28.92MW，18.84 MW，TCN-LSTM 预测模型的预测效果更好，表现出较好的普适性。为直观了解预测结果，从2012 年每个季节随机选取连续1 周的结果进行展示分析，结果如图7 所示，受篇幅影响，此处仅展示夏季的预测结果。

图7 不同模型在夏季的预测曲线Fig.7 Forecasting curve of different models in summer

由图7 可知，TCN-LSTM 预测模型的负荷预测曲线更贴近实际负荷曲线，特别是在峰谷时段，说明TCN-LSTM 预测模型具有更好的预测效果。进一步计算MAPE 和MAE 指标，结果如表8 所示，其中春季为2012-03-11 至2012-03-17；夏季为2012-06-14 至2012-06-20；秋季为2012-10-20 至2012-10-26；冬季为2012-12-08 至2012-12-14。

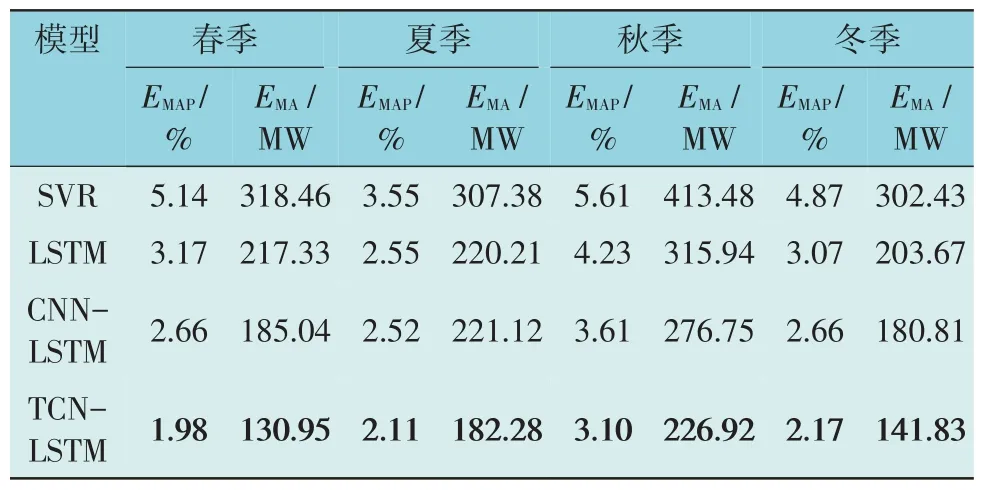
表8 不同模型在不同季节的预测结果Table 8 Forecasting results for different models in different seasons

由表8 可知，在不同季节，TCN-LSTM 预测模型的EMAP和EMA均比SVR，LSTM，CNN-LSTM 预测模型的小，表明TCN-LSTM 预测模型在不同季节的预测效果均优于其它预测模型，季节鲁棒性更强，具有良好的稳定性。

5 结论

为进一步提升电网短期负荷预测的精度，本文提出了一种基于TCN-LSTM 和气象相似日集的电网短期负荷预测方法。主要结论如下：

1）考虑气象相似日集作为预测模型的输入特征，可以充分挖掘不同气象相似日蕴含的信息，有利于提升短期负荷预测精度。

2）TCN-LSTM 预测模型组合了TCN 和LSTM网络的特点，通过TCN 进行特征提取后输入至LSTM 网络，加强了对特征信息的挖掘，得到了更好的预测效果。

本文提供的数据集有限，可能存在所提预测模型在某些数据集中的预测结果不是最理想的，因而组合不同预测模型的预测结果可能有助于提高负荷预测精度，这值得进一步研究。此外本文的预测形式为点预测，后续可进一步应用到区间预测和概率预测，为调度决策提供更丰富的不确定性信息。