多元线性回归的英文文本难度估计模型

安康，张勇博，黄泽

（杭州电子科技大学，浙江 杭州 310018）

0 引 言

阅读是人类获取信息和知识的重要途径。然而，超出或低于读者水平的文本可能对基本文的提取造成阻碍。所以衡量文本的难度指数至关重要。

目前，对于文本难度的研究由于时代的需求，现在越来越火热。最通用的公式是Flesch-Kincaid Grade Level，但是这个公式的表达过于简单，只有两个变量，这导致公式的普适性以及稳定性较差。同时，也只能体现文本的客观难度，没有考虑到个人差异例如文化差异等带来的主观因素。

我们想优化这个模型，从单词，句子，文章三个维度设置了8个评估指标，增加变量个数来提高模型稳定性，应用多元线性回归的方法，确定变量系数。并且我们在模型中加入了主观因素，将个人差异带来的文本难度差异能够量化出来。

1 模型参数选择

在评估英语文本的阅读难度时，我们参考了多种因素和资料，我们将这些因素划分为3个纬度：词汇难度，句子难度和文章难度。

1.1 词汇困难纬度

在词汇困难纬度选择了2个指标，分别为常用词指数和音节指数，这两个指标可以衡量一篇文章在词汇领域内的阅读复杂程度。

1.1.1 词汇常用指数

通常情况下，日常口语的交流只需掌握2 000个常用词汇就够了。出现过多的生僻词会增加词汇难度，增加阅读难度。因此，将词汇困难纬度中词汇常用指数定义为：

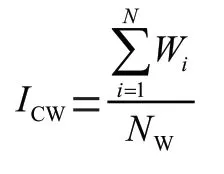
其中，表示的是一篇文章的常用词指数，W表示的是第个单词在数据库中出现次数与数据库总词数之比，表示文章的总词数。

1.1.2 音节难度因素

往往一个单词的音节数越多，该单词越复杂，该英语文本的词汇难度就越高，从而影响一篇英语文本的阅读难度，因此，在词汇困难领域中音节指数定义为：

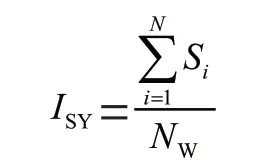
其中，表示一篇文章的音节指数，S表示的是第个单词的音节数量，表示文章的总词数。

1.2 句子难度纬度

在句子维度，句长指数，句子相似度指数和从句指数这3个因素，在很大程度上影响了一篇英语文本的阅读难度。

1.2.1 平均句长指数

一篇英语文本平均句长越长，该英语文本的句子难度就越高，从而影响这篇英语文本的阅读难度，因此，在句子困难纬度中平均句长指数定义为：

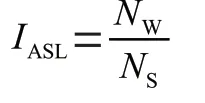
其中，表示一篇文本的平均句长指数，表示该文本总单词数，表示该文本总句子数。

1.2.2 句子相似度指数

文章相似程度句子出现的越多，该英语文本的句子难度就越高，从而增加一篇英语文本的阅读难度，因此，在句子困难领域中相似度指数定义为：

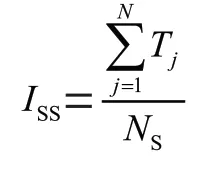
其中，表示一篇文章的相似度指数，T表示的是第个句子中出现相似词的词数，表示文章的总句子数。

1.2.3 从句指数

过多的长短句产生的子句结构和从句结构也会增加句子的理解难度，从而影响一篇英语文本的阅读难度，因此在句子困难领域中从句指数的数学表达形式为：

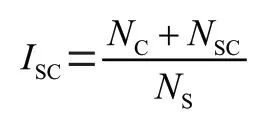
其中，表示一篇文章的从句指数，表示子句数量，表示带有连接词的从句数量，表示总句子数。

1.3 文章难度

在文章困难领域，文章总词数，信息熵指数和逻辑困难指数3个指标。这些关键的指标会对文本难度造成影响。

1.3.1 篇幅长度指数

我们看到英语文本时，第一反应是这篇文章的篇幅，所以，过长的文章篇幅会增加文章的难度。所以，我们可以简单地将文章困难领域中总词数定义为。

1.3.2 信息熵指数

引入信息熵的概念，文本的信息熵越大，表明文本难度越大，从而影响一篇英语文本的阅读难度。因此文章困难领域中信息熵指数定义为：

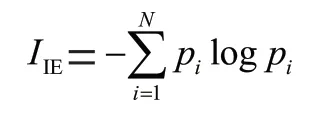
其中，表示信息熵指数，即信息熵总量。

1.3.3 逻辑难度指数

一篇文章出现的从句代表词和逻辑词数量越多，该文章的逻辑结构越复杂，会大大增加该文章的困难度。因此在文章困难领域中逻辑难度指数定义为：

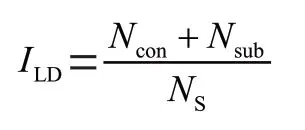
其中，表示一篇文章的逻辑难度指数，表示从句代表词数量，表示逻辑词数量，表示

1.4 代码实现

我们得到了上述变量的数学形式后，用Python将文本中的数据提取出来，进行量化。图1、图2是代码实现。

图1 代码第一部分

图2 代码第二部分

2 模型建立

在定义了3个维度的指标后，我们以这8个指标为变量，建立了基于多元线性回归的WSA模型。

WSA模型的分数可以衡量一篇英语文本的阅读难度，分数越高，表示该文本越难读懂。WSAscore的数学表达形式为：

其中，～表示各项指标的权重参数，为多元线性回归的常数。

3 模型参数确定

首先，假设新概念英语的文章难度是均匀递增的，难度指数定为0～100。再去除新概念英语训练集中某些专门学习从句结构、逻辑结构的篇章。同时我们认为高考英语试卷的难度就是标准文件的难度左右，设在70左右。

3.1 相关分析

其中，diff表示因变量。由表1中可以很清楚地看到，每一个指标和diff都有较强的相关性，所以可以进行多元线性回归。

表1 相关性分析结果

3.2 初次计算

我们将训练集数据运用多元线性回归的方法，求得WSA模型得分的各项指数权重以及常数，结果为：

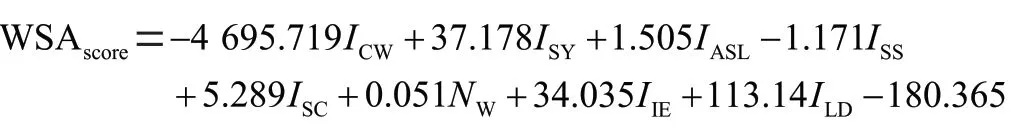
在用SPSSPRO求得各项指标的权重后，我们进行了各项检验分析，我们发现句子相似度指数的P值为0.742，远超出统计学的标准，不符合显著性，因此我们剔除句子相似度指数这一项指标。

3.3 再次计算

最后我们再次将训练集数据运用多元线性回归的方法，求得除去句子相似度指数的另外7项指数权重以及常数，结果为：

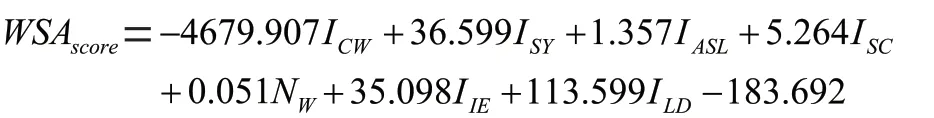
拟合图如图3所示：

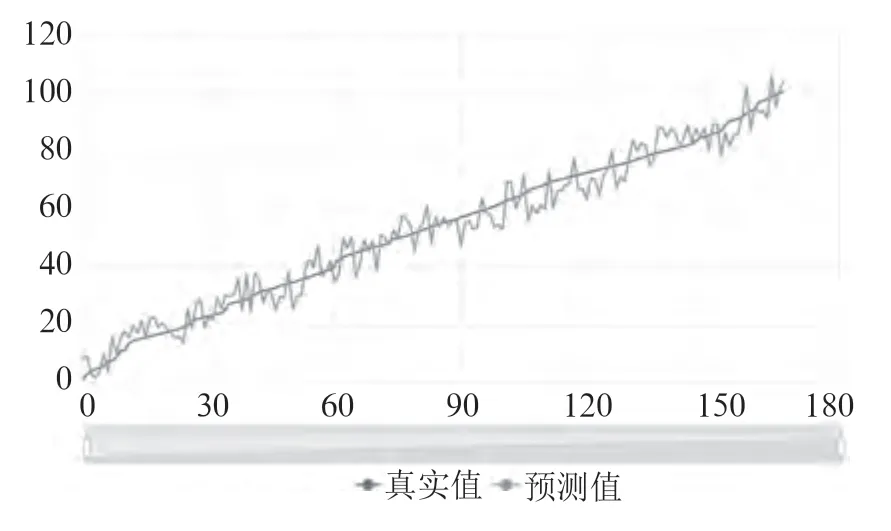
图3 效果拟合图

最后，检验得到此处7项指标的p值均＜0.01，说明自变量参数检验完全合理，结果非常显著。VIF值全部小于10，且除了平均句长指数的VIF＞5外，其余6项指标的VIF均小于5，满足严格意义上的VIF范围。R调整后的数值为0.96，代表模型构建非常优秀。

3.4 模型验证

我们选取2022年的湖州英语中考的4篇阅读，英语高考全国卷甲卷的4篇阅读和CET-6的4篇阅读作为测试集，带入之前的代码后，得到表2所示的数据。

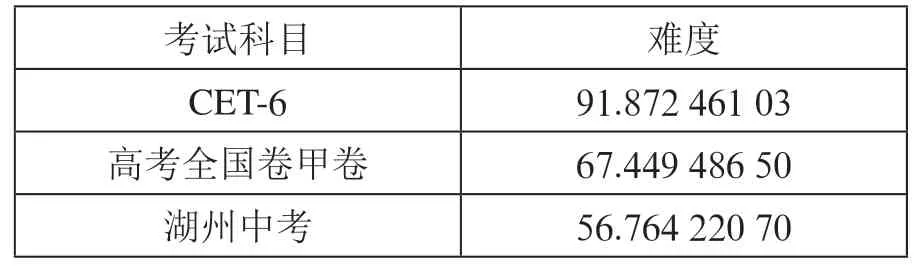
表2 测试集难度

我们可以看到，六级难度大于高考难度，高考难度大于中考难度，这与实际情况一致，所以我们认为模型的实用性较好。

3.5 灵敏性分析

之前我们假设平均分布的方式得到难度值，下面假设正态分布的方式得到难度值，得到新的一个模型，最后将测试集带入上述模型中，得到CET-6，中考和高考的误差值2.39%，1.72%，2.21%。由此可见，两者的差值位于2%左右，误差非常小。所以，对于难度方式分布敏感度很小，模型很稳定。

4 模型推广

然而，阅读难度往往受到阅读者个体的影响。不同国家的人对比测试，往往测试结果会出现很大的偏差，这是因为测试者个体因素导致的偏差。因此我们将WSA模型扩展到个体因素领域，引入文化差异性的概念，提出新的WSAP模型。

4.1 文化差异性与客观阅读难度的比例

我们将文化变异性定义为主观阅读困难（以OD表示）和客观阅读困难（以SD表示）。WSAPscoe是总难度系数，它是主观阅读困难和客观阅读困难的总和。

WSAP=OD+SD

首先通过查找文献，参考一组时间跨度为2年的文化差异性教育的研究成果，该研究结果如表3所示。

表3 文化差异性教育结果

选取两个班级，一个作为参考班，不接受文化差异性教育。另一个为试验班，接收文化差异性教育，并且定期进行阅读能力的测试。通过对比发现，试验班的阅读分数比参考班参考班增加了20%。

定义接收文化差异性教育前的阅读得分为，文本翻译能力为，之后的阅读得分为，文本翻译能力为。接收文化差异性教育之前总难度系数为WSAP1，接收之后的总难度系数为WSAP2。

1.2（OD+SD）=OD+SD

我们可以得到：1.2WSAP=WSAP

假设接收文化差异性教育后的主观阅读难度为0，即CD=0，接收前的主观阅读难度为1，即CD=100。

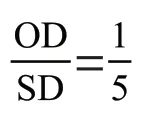
所以我们认为主观难度和客观难度权重之比为1：5。即为1/6，为5/6。

4.2 WSAP模型建立

我们引用Geert Hofstede的文化距离理论，用于体现文化差异性：

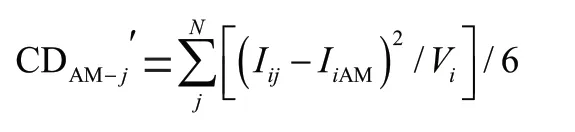
其中：为6个文化维度之一，6个维度分别为权利差距、个人主义或集体主义偏向、不确定性规避指数、男性偏向或女性偏向、长期导向和放纵与约束。CD是东道国家与美国的文化距离值，I是关于国家维度的文化维度评分，AM代表美国，V是i维度所有东道地文化距离的方差。最后对CD的值进行标准化处理，并使其满足正态分布于0～100。表4列出了几个国家的CD值。我们对OD和SD进行以下的定义：

表4 多个国家CD值

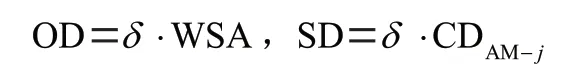
所以我们建立完整的总难度模型WASP：

4.3 模型计算

我们用继续使用WSA模型的测试集来检验WASP模型，其对象为中国人，东道主国家是美国，通过查找表4得到CD的值为87.24。带入模型中得到CET-6、中高考难度分别为61.84、70.75、91.10。

最后，我们将20%的权重改变从5%到30%，发现其差值都低于3.8%，说明模型稳定。

5 结 论

我们应用多元线性回归模型，得到了英文文本难度估计模型WSA。并进行推广，得到了WSAP模型。我们认为两种模型可应用不同的情况，将WSA应用于只需要关注文本自身难度的情况下，将WSAP应用于需要考虑个人因素对于文本难度的影响时。

最后，我们认为该方法的创建可以应用到其他语言，比如中文等其他语种。为所有文本的难度估计提供了一种可行的方法。