复式断面明渠流能量及动量校正系数研究

曾 诚，邱 斐，丁少伟，周 婕，徐剑波，王玲玲，尹雨然

(1. 河海大学 水利水电学院，江苏 南京 210098； 2. 华设设计集团股份有限公司，江苏 南京 210014； 3. 河海大学力学与材料学院，江苏 南京 211100； 4. 中国一冶集团有限公司，湖北 武汉 430081)

复式断面是平原地区河道断面的常见形式。主槽和边滩区域水体的水深和糙率差异，导致复式断面内的流速空间分布不均匀，采用平均流速进行水力计算时误差较大。引入能量和动量校正系数描述河道断面流速分布的不均匀性，可提高水力学计算精度。国内外多位学者对复式断面的能量及动量校正系数进行了试验和理论研究。Luo等[1-3]先后通过水槽试验进行实测分析，研究表明能量与动量校正系数受滩槽水深比的影响较大，随着水深比的增大，两个系数逐渐减小。此外，能量与动量校正系数与断面的对称性及形态（包括宽度比、宽深比、断面形状等）有关。Pantelakis等[4]通过对希腊北部3条河流的实测，证实这两个系数始终大于1，并且数值受水下植被和分区的影响。在数值模拟方面，前人的研究成果较少，Parsaie[5]利用单通道法（SCM）和分通道法（DCM）研究了能量校正系数与水深的关系，证明在考虑能量校正系数时，弗劳德数和比能数值更大。在国内，陈界仁等[6]利用划分单元求和方法计算了3种典型断面的动量校正系数，并证明了动量校正系数是宽深比的函数。杨克君等[7]针对滩槽交界处的表观剪切力进行研究，论证了横向动量校正系数和动能损失率与复式河槽断面形态之间的关系。

此外，滩地植被是影响复式河道流速分布的主要原因之一，滩地植被的存在会增加河道的整体阻力，改变水流的紊动结构及流速分布规律。Yang等[8]通过水槽试验，证明了不同的滩地植物种类对水流紊动强度的影响不同，且滩地种植植物后，水流的紊动强度增强。Hamidifar等[9]采用水槽试验，利用刚性桩模拟植物，探究了非对称复式河道中，能量和动量校正系数与植被密度的关系。Kubrak等[10]在矩形水槽中模拟了水草、刚性及柔性植物茎秆，发现随着水槽水深和茎秆密度的增加，能量和动量校正系数显著增加。陈正兵等[11]采用EFDC模型模拟滩地植被对河道水流的影响，发现植被的存在会影响河道横向流速分布，使水流有向主槽集中的趋势。闫静等[12]利用圆柱铝棒模拟刚性植物，利用水槽试验对含非淹没、淹没植物的明渠水流进行分析，证明植物的淹没度及植被密度对明渠流速分布存在影响。

综上所述，前人研究大多基于传统的物理模型试验，对一些点或者面的监测存在局限性。数值模拟方面，前人多采用基于雷诺时均的涡黏紊流模型，忽略了紊流运动的若干微小细节，而采用大涡模拟方法能够精确地还原流场，获得更为精细的数值模拟结果。本文采用壁面建模的大涡模拟（WMLES）方法，能克服传统大涡模拟方法在模拟高雷诺数工况下近壁面需要足够细密网格的问题，无需对边界层区域（主槽底面与滩地底面）进行加密，降低了计算成本。采用基于WMLES方法的三维数值模型对不同水深比和植被密度工况下的复式断面明渠流进行大涡模拟研究，分析能量及动量校正系数的分布规律。

1 数值模型

1.1 控制方程

计算区域内水流运动满足连续方程和动量方程，其过滤形式如下：

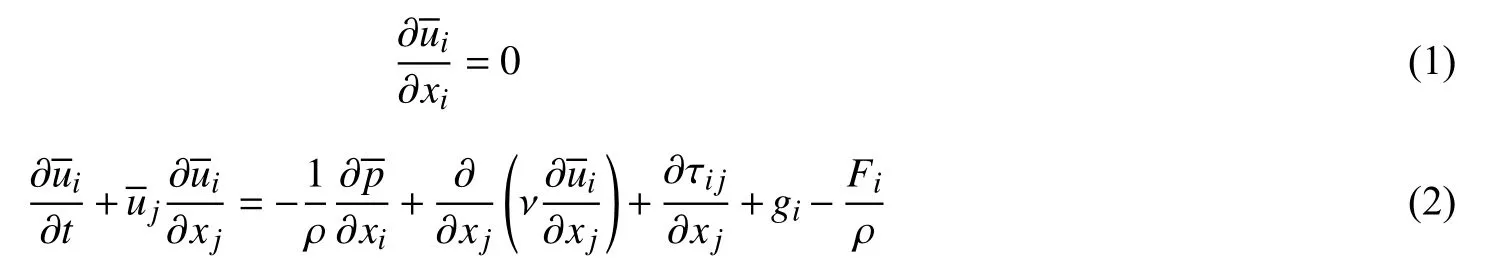
1.2 植被水流数值模拟方法

植被水流的数值模拟，主要采用以下两种方法对植物进行直接模拟或间接模拟。直接模拟法是将植物模拟为多柱体模型，在计算水体的水动力特征时，将每一植物单元都考虑在内，如Stoesser等[13]采用此种方式进行研究。此方法能够模拟植物群落内部的流动，但需要更为精细的网格。间接模拟又称阻力模型法，如Neary等[14]使用的模型，将植物所在区域视为阻力区域，用平均阻力代替植被对水流的作用，其优势是能大大降低网格数量，提高计算效率。本文采用阻力模型法对含非淹没刚性植被的明渠水流进行研究。

模拟中将植物简化为细长圆柱杆，利用拖曳力来概化植物对水流的阻力效应。对于单个植物，其单位高度的植物阻力表达式为：

式中：Cd为植物的阻力系数；bv为水中单株植物的平均直径。结合柱体绕流的阻力特性，可得植物区域单位体积流体的阻力公式为：

式中：N为单位面积的植物数量。选取阻力参数frk（=CdbvN）表征植被密度对水流的影响。Dunn等[15]的试验研究结果表明，明渠中植物的Cd值在垂直方向上是变化的，其取值范围为0.98~1.28。本文取阻力系数Cd=1.13。

1.3 数值方法及边界条件

为保证流场充分发展，选取SSTk-ω计算的稳态场作为WMLES计算的初始流场。离散格式选取具有三阶精度的QUICK格式，速度与压力解耦采用PISO算法。水流入口与出口均设为周期性边界，自由水面采用刚盖假定，固体壁面为无滑移边界。

本文研究对象为复式断面明渠，水深比的变化范围为0.10~0.75，参考Tominaga[16]的物理模型试验进行模拟验证及分析。物理模型试验在长为12.5 m的复式断面水槽中进行，水槽总宽度B=0.4 m，主槽宽度b=0.2 m，采用激光多普勒测速仪测量流速。工况验证参见文献[17]。该模型经过充分率定，将模拟结果与试验测量值相比较，结果表明WMLES方法能够准确模拟平均流速、床面切应力、紊动强度、紊动能和雷诺应力分布，并且能够准确模拟出断面内的二次漩涡结构。图1为水深比hr=0.5工况的数值模拟计算区域，x、y、z轴正向如图1所示，坐标原点位于主槽上游侧渠底。模拟选取单侧滩地的非对称复式断面结构，可减少网格数量，节省计算成本。

图1 计算区域示意[17]Fig. 1 Schematic diagram of calculation area[17]

计算区域采用六面体网格进行剖分，x、y、z方向均采用结构化网格，未对网格进行加密，对于本文所涉及的 5种水深比工况（hr=0.10、0.17、0.25、0.50、0.75），经过网格无关性验证，确定网格数在 1.44×106（hr=0.10 工况）至 2.24×106（hr=0.75 工况）之间。

针对滩地植被密度工况，网格剖分、边界条件和初始条件与水深比0.50工况一致。以水深比0.50的无植被工况下的流场作为初始流场，在计算约50个流动周期（1个流动周期T=10H/V，其中H为主槽水深，V为断面平均流速）开始进行时均统计，时均统计时长均为70个流动周期。模型的数值方法、边界条件和模型验证等详见文献[18]。该数值模型已被成功应用于水深比对复式断面明渠流的水流结构及紊流特性的影响研究。

2 能量及动量校正系数计算

能量校正系数又称为科氏系数，由法国工程师Coriolis于1836年提出，其计算式如下：

动量校正系数又称为波辛尼斯克系数，由法国数学家Boussinesq于1877年提出，其计算式如下：

V为断面平均流速，计算式如下：

式中：A为某一特定过流断面的面积；V为该断面的平均流速；ΔA为模拟断面中单个面网格单元的面积；i为单元号；n为单元数；v为离散单元ΔA所对应的断面平均流速值。

能量与动量校正系数在表达式上具有相似性，在物理意义上，均可描述某一过水断面流速分布的不均匀程度，其值越大，流速分布越不均匀。

3 工况设置

表1为本次模拟研究的计算工况。为分析水深比与复式断面明渠能量及动量校正系数的关系，拟定了5组不同水深比工况进行模拟计算。为分析滩地植被密度对复式断面明渠流能量及动量校正系数的影响，拟定了3组不同滩地植被密度工况。

表1 计算工况Tab. 1 Computation conditions

4 计算结果与分析

4.1 水深比对校正系数的影响

图2是通过WMLES得到的断面流速分布，x轴通过主槽水深H进行无量纲化。整体来看，主槽流速大于滩地流速，在hr≤0.25时，这一现象尤为显著，当水深比hr≥0.50时，流速差距逐渐减小，在水深比hr=0.75的工况下，滩槽的流速分布差异已不明显，这是由于在主槽水深不变的情况下，随着滩地水深的不断增大，复式断面明渠流动趋于单一河道的均匀流动。此外，由于壁面阻力的存在，在接近主槽和滩地侧壁时，流速迅速减小。在滩槽交界面处，5组曲线均有明显突变，这表明此处二次流及水体横向紊动增强，导致横向的动量输运，引起流速降低。

图3为5种水深比工况下复式断面明渠流能量和动量校正系数的横向分布，计算结果的横坐标采用主槽水深H进行无量纲化。如图3所示，能量校正系数比动量校正系数对水深比的变化更为敏感，且前者的数值始终大于后者。整体上二者沿断面的变化趋势相似，但变化幅度不一致。主槽内，随着水深比的改变，α与β值基本保持稳定。由于二次流主要产生于明渠固壁拐角和近岸附近，在滩槽交界处二次流最明显[19]，因而能量和动量校正系数在此处产生突变。而在滩地内，α和β值与主槽内数值对比相差较大，特别是在水深比较小的工况中，这种差异尤为明显。随着水深比的增大，主槽和滩地α与β值的差异逐渐减小，最终均趋近于1。其次，如图2所示，由于边壁阻力的作用，在靠近壁面处流速骤减，造成流速变化幅度较大，不均匀程度增大。因此，在壁面附近校正系数分布曲线出现较大程度的弯曲。

图2 断面平均流速分布Fig. 2 Distribution of average velocity

图3 不同水深比下复式断面能量和动量校正系数分布Fig. 3 Distribution of correction coefficients of energy and momentum in compound sections with different flow depth ratios

主槽、滩地及总复式断面能量及动量校正系数随水深比的变化见图4。三者的变化趋势总体一致，都呈减小趋势。滩地的能量及动量校正系数最大，且变化幅度较大；主槽的校正系数最小，且随着水深比的改变，其数值基本保持稳定，能量校正系数接近于1.1，动量校正系数接近于1.03；总断面的能量及动量校正系数介于二者之间，且当hr≥0.50时，散点几乎重合，原因在于滩、槽流速大小及分布趋于一致。

图4 能量及动量校正系数随水深比的变化Fig. 4 Values of the kinetic energy and momentum coefficients against different flow depth ratios

基于本次模拟计算的结果，采用回归分析，得到能量和动量校正系数与水深比hr之间的拟合公式分别如式（8）和（9）所示：

4.2 滩地植被密度对校正系数的影响

如图5所示，在滩地布置植被后，由于植物的阻水作用，滩地的过流能力减弱，在流量不变的情况下，滩地的高流速区向主槽方向移动，所以与无植被工况相比，滩地断面平均流速曲线由上凸变成下凹。随着植被密度的增大，主槽流速显著增大，滩地流速明显减小，并且其差值随着植被密度的增大而增大。在滩槽交界处，由于水流掺混作用明显，横向紊动增强，导致该处垂向平均流速减小。

图5 断面深度平均流速分布Fig. 5 Average velocity distribution at section depth

在水深比为0.50工况的基础上，通过改变滩地植被阻力系数，研究了复式断面明渠能量和动量校正系数的横向分布。为便于计算结果的分析对比，也列出了水深比为0.50条件下滩地无植被情况下的计算结果。如图6所示，能量校正系数变化幅度仍大于动量校正系数，且前者的数值始终大于后者。整体变化趋势与水深比工况类似。在主槽内，随着植被密度的增大，α和β的变化幅度不大且比较接近。在滩槽交界面处，由于滩槽水体的掺混作用骤增，流速分布的不均匀程度增大，曲线产生明显转折。在滩地内，整体而言，α和β比主槽内大。在滩地左侧，其流速梯度随着植被密度的增大而明显增大，故滩地的系数横向分布不均匀，左侧靠近交界面处出现峰值。其次，由于边壁阻力作用，靠近壁面处流速变化率大，不均匀程度变大，在靠近壁面处校正系数分布曲线呈上升趋势。

图6 不同植被密度下复式断面能量和动量校正系数分布Fig. 6 Distribution of correction coefficients of energy and momentum in compound sections with different densities of vegetation

能量及动量校正系数随植被密度的变化如图7所示。可见，能量和动量校正系数的变化趋势大致相同，在数值上，α变化范围更大。在水深比0.50的情况下，滩地无植被，总复式断面的系数值介于主槽和滩地的数值之间，而在有植被工况中，复式断面的系数值均大于主槽和滩地的系数值。从图5可知，在无植被的情况下，主槽和滩地流速分布较为接近，滩地流速略低于主槽流速。而随着植被密度的增大，因为植被的阻水作用致使主槽流速越来越大，而滩地流速越来越小，滩槽流速差异变大。总断面与滩地和主槽相比，其流速分布的不均匀程度最高。其次，随着植被密度的增大，能量和动量校正系数的数值随之增大，原因在于随着植被密度增大，滩、槽的深度平均流速分布曲线的曲率不断增大，证明局部流速梯度增大。

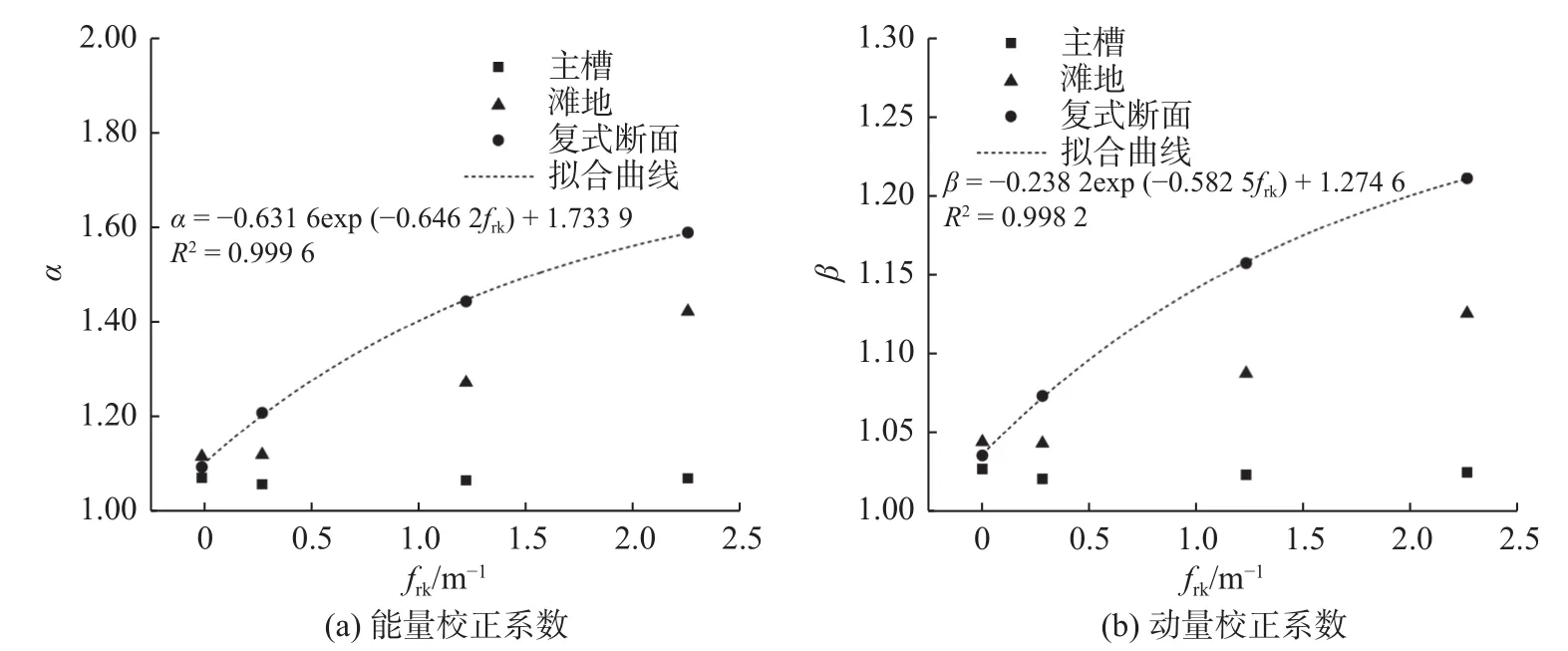
图7 能量及动量校正系数随植被密度的变化Fig. 7 Values of the kinetic energy and momentum coefficients against different densities of vegetation

根据本次模拟计算的结果，经回归分析，拟合得到能量和动量校正系数与植被密度阻力参数frk之间关系如下：

4.3 能量与动量校正系数间的关系

由能量和动量校正系数的定义可以得出：α≥β≥1。在矩形断面明渠的水力学计算中，为简化计算，通常将能量和动量校正系数取为1。从本次模拟计算的结果可以看出，对于复式断面明渠流动而言，河道内流速分布的不均匀性增大，导致能量和动量校正系数明显大于1。若对能量及动量校正系数预测不足，会导致天然河流或人工河道的水力相关计算中出现较大误差。根据模拟工况所得结果，对能量校正系数值和动量校正系数值进行分析，发现能量校正系数与动量校正系数存在线性关系（见图8），如式（12）所示：

图8 α与β关系分析Fig. 8 Relation between α and β

式（12）可在已知能量或动量校正系数值情况下预测相同工况条件下另一校正系数值。由于影响复式断面流速分布的因素较多，该式仅适用于非对称矩形复式断面中能量及动量校正系数的预测；对于其他形状断面的能量校正系数和动量校正系数的关系，有待后续进一步研究。

5 结 语

（1）复式断面明渠流的主槽与滩地的能量和动量校正系数存在显著差异。在滩槽交界处，能量校正系数α和动量校正系数β存在突变；在主槽内，α和β随着水深比的增大无显著变化；而在滩地内，α和β随着水深比的增大逐渐减小。随着水深比的增加，复式断面明渠流中能量及动量校正系数的横向分布趋向于矩形断面明渠流中的横向分布。

（2）随着滩地植被密度的增大，对滩地水流的阻水增强，导致主槽流速愈大，滩地流速愈小，断面流速分布不均匀程度增大；主槽、滩地及复式断面的能量与动量校正系数值均有明显增大。

（3）与动量校正系数相比，能量校正系数对水深比和滩地植被密度的变化更为敏感，其变化幅度更显著，且数值上始终大于动量校正系数。