基于Copula函数的大通站水沙特征分析

黄宇明 ，缴 健，窦希萍，郭海军，丁 磊

(1. 南京水利科学研究院 港口航道泥沙工程交通行业重点实验室，江苏 南京 210029； 2. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072)

近年来，随着人类活动对自然生态系统影响的不断增强，流域下垫面情况发生显著变化，加之全球范围内的极端天气频发，使得水文序列表现出多时间尺度的随机性和突变性[1]。流域水文要素如降雨、径流、气温和来沙量等发生剧烈变化，水文一致性过程遭到破坏。水、沙要素响应过程一直是河流研究工作者关注的重点，河流水沙变化的一致性关系到河床冲淤、深水航道疏浚等工程实际。因此，开展河道水沙关系突变性分析，对水库稳定运行、河道规划管理及维持变化环境下的水沙关系动态平衡过程具有重要意义。

目前，针对单个水文要素的突变分析，最常用的方法有Mann-Kendall秩相关检验法、滑动F检验法[2]、滑动T检验法[3]及Hurst系数法[4-5]等。二变量条件下的水文变异分析则一般采用滑动偏相关系数法[6]或Copula函数理论。其中，Copula函数作为一种能够将多个不同变量拟合起来的简单有效的实用分析工具，已被广泛应用于多变量水文分析研究[7]。李艺珍等[1]采用滑动Copula函数研究了变化环境下金沟河流域径流与气象因素关系的变异情况；李艳玲等[8]结合滑动窗口算法和Copula函数理论，对流域降雨径流关系变异进行了研究分析；郭爱军等[9]利用Copula函数建立了水沙联合分布，分析了水沙组合的变化特征；何兵等[10]基于滑动Copula函数理论分析了新疆内陆干旱河流的水文气象要素的变化特性。

综上可见，Copula函数方法是现阶段多变量水文变异分析最常用的。基于变量序列的相关参数突变分析，将水文序列根据突变点划分为不同长度的子序列并分别采用Copula函数建模，能够有效表征各子序列的不同特性，但同时也增加了各子序列边缘分布组合方式的多样性，而对基于Copula理论的多变量水文分析的边缘分布不确定性分析却缺乏足够的研究。因此，本文采用滑动窗口方法计算大通水文站水沙组合1965—2019年逐月序列的相关系数，分析水沙组合变异特性，基于Copula函数理论构建水沙联合分布模型，计算水沙同步、异步的遭遇概率，并对不同序列水沙组合的边缘分布函数选取不确定性问题进行分析，以期揭示在人类活动影响下的大通水文站水沙组合序列演化规律及突变特征，并为流域水沙规划、滩涂治理、深水航道泥沙冲淤平衡及水资源调控等提供参考。

1 研究方法与理论

根据Sklar理论[11]，Copula函数的一般表达式可描述如下：

式中：Xi为不同的随机变量；F(xi)=ui为不同随机变量的边缘分布函数；θ为Copula 函数的相关参数。表1列举了4个不同的Copula函数类型，其中Clayton、Frank和G-H是3种常见的阿基米德Copula函数；Gaussian是将标准正态分布与二重积分结合的Copula函数，Ф−1是标准正态分布函数的逆函数。

表1 4种不同的Copula 函数Tab. 1 Four different Copula functions

采用欧氏距离d评价Copula函数拟合优度，其表达式如下：

欧氏距离d越小，则Copula函数模型的拟合度越高。分别是水沙序列的理论频率和经验频率，经验频率的计算如下：

对于常见的二变量水文分析如洪水峰、量组合，降雨、径流组合或者干旱强度、烈度等，需要考虑的有联合(OR)、同现(AND)、Kendall及生存Kendall[12]等4种不同的设计重现期。其中，联合(OR)重现期是指二变量中至少1个变量大于其对应设计值的概率，表达式如下：

与传统的单变量水文分析不同，在多变量水文分析中，在给定设计重现期T或设计频率P的情况下，同一个设计频率对应着无数个变量组合，最大可能组合是其中最受关注的一个。

式中：c(u,v)、f(x)和f(y)分别是Copula函数和边缘分布函数的概率密度函数。

以大通水文站1965—2019年的55年径流量和输沙量资料为基础样本，进行滑动窗口计算，具体如下：（1）确定滑动步长L，滑动窗口长度W；（2）保持滑动窗口W不变，从水、沙序列的第1个数据开始，以基本步长L滑动窗口，计算每个窗口内两个序列的相关参数；（3）根据水沙序列的相关参数变化情况进行水沙变异判断；（4）采用Copula函数对每一段序列进行建模分析。

2 研究区域及数据

长江口是连接长江干流与外海的重要部分，广义的长江口是指从安徽大通水文站到外海50 m等深线长660 km的河段（见图1）。 长江口是典型的喇叭形河口，由于地球自转偏向力的影响，长江河口北岸冲刷而南岸泥沙淤积，从而形成了“三级分汊，四口入海”的河口地貌特征[13-14]。大通水文站是长江口区域的重要水文站点，多年数据统计分析表明，大通站以下的长江干流入流量仅为大通水文站径流量的3%，因此可以认为大通水文站的水沙情况基本上反映了长江干流的来水来沙特征[15]。本文收集了1965—2019年大通水文站逐月径流及相应的来沙量资料，作为实测样本数据进行分析计算。

图1 长江口示意图Fig. 1 Schematic diagram of the Yangtze River estuary

3 水沙变化特征分析

3.1 水沙关系突变判别

采用滑动窗口算法计算水沙组合的Spearman秩和Kendall秩相关系数，基本步长L取12个月，6个不同的滑动窗口W取为24、36、48、60、120 和240个月。根据相关参数的波动情况来判断水沙组合的变异特性，计算结果如图2所示。从图2可以看出，当滑动窗口W较小（W=24）时，相关参数上下波动较为频繁，且波动范围也相对较大；相反，当滑动窗口W较大（W=240）时，相关参数波动范围较小。因此，在滑动窗口取值偏小或偏大的情况下，并不能准确地判断水沙组合的突变年份。而当滑动窗口W取为36、48、60及120的情况下，可以发现水沙组合的相关参数在1979年和2000年波动较大且具有一致性。

图2 变化滑动窗口下大通站径流量与来沙量相关系数Fig. 2 Correlation coefficient of runoff and sediment discharge under the changing sliding window of Datong Station

3.2 水沙关系突变前后分析

根据水沙关系变异分析结果，以1979和2000年作为划分点，将大通站水沙序列分为1965—1979年、1980—2000年和2001—2019年3个阶段。采用PE3分布对分段后的径流量序列和输沙量序列进行拟合，并计算3个阶段重现期为1~100 a对应的水、沙特征值，计算结果见表2。由表2可见，从1965到2019年，径流量与输沙量均呈减少趋势；在2000年之前，大通站水沙序列表现出相对稳定的状态；2000年后，水、沙序列均表现出减少的趋势，其中，来沙量减少幅度达到200%以上。造成长江干流输沙量在2000年以后大幅减少的主要原因可以归结两方面：一是以三峡工程为主的大型水利工程相继建成运行；二是流域森林植被覆盖率大幅提升。研究表明，相较于1985—2000年，在2001—2013年间由于水库建设使得输沙量下降达到83.1%，而长江流域植被覆盖率上升导致的输沙量下降占实际输沙量下降的18.0%[16]。同时也可看出，1965—1979年和2001—2019年的水沙序列均有较好的变化一致性，而1980—2000年的水沙序列相较于前一个阶段却表现出了水增沙减的趋势，造成这一现象的原因可能是由于在1980年到2000年，长江流域处于水能资源开发的高潮时期，同时流域环境破坏使得植被覆盖率降低，且在20世纪90年代后期遭遇了极端洪水年份，破坏了这一阶段水沙关系变化的协调一致性。

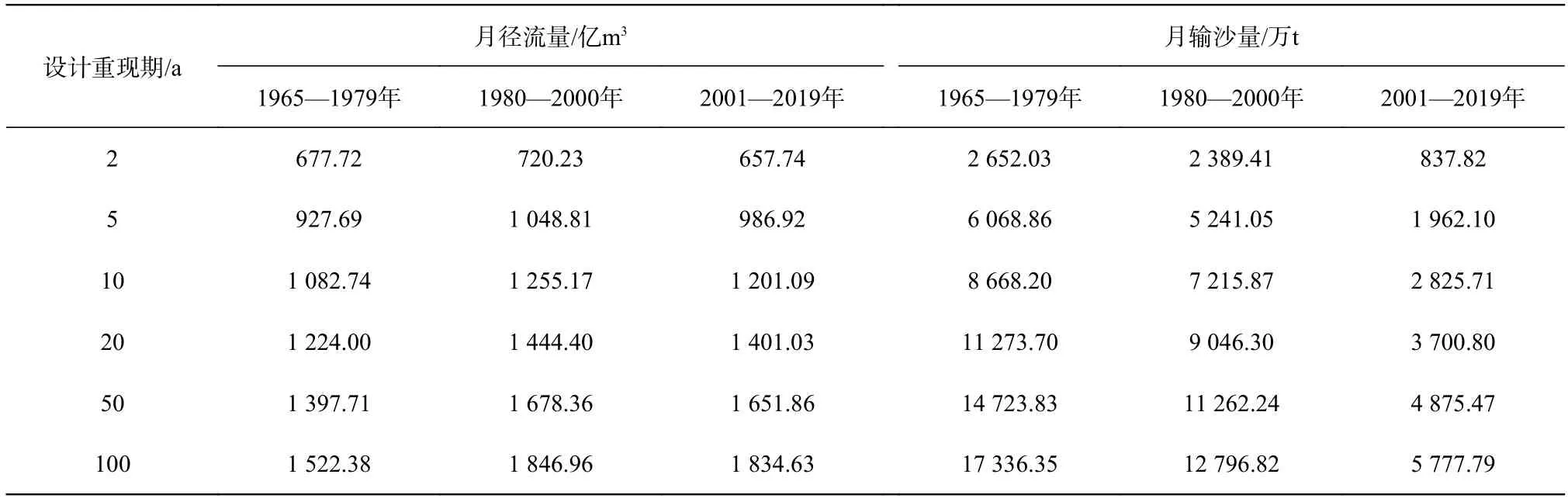
表2 水沙关系突变前后特征值分析Tab. 2 Analysis of eigenvalues before and after the mutation of runoff-sediment relationship

采用指数方程对3个阶段的水沙序列进行函数拟合，计算结果如图3所示。3个阶段的R2分别是0.785 6、0.745 0和0.708 5，但1980—2000年阶段的拟合函数表达式过于复杂，且拟合曲线趋于直线，可能由于数据离散化太严重导致了过拟合，与根据表2计算结果分析的水沙数据不协调相一致。

图3 不同阶段大通站径流量与来沙量关系Fig. 3 Relationship between runoff and sediment discharge in different periods of Datong Station

4 水沙联合特征及不确定性分析

4.1 水沙联合分布特征分析

根据水沙突变分析结果，将水沙序列分为1965—1979年、1980—2000年和2001—2019年等3段。采用PE3、 广义帕累托(GPD)和广义Logistic (GLD)3种分布函数分别对水沙序列进行边缘分布函数拟合，并采用AIC信息准则和RMSE对边缘分布函数拟合优度进行评价，计算结果见表3。根据AIC值和RMSE值越小拟合越优的评价准则，1965—1979年阶段的水沙序列最优边缘分布是PE3-PE3，而1980—2000年和2001—2019年阶段的水沙序列则是PE3-GPD拟合最优。

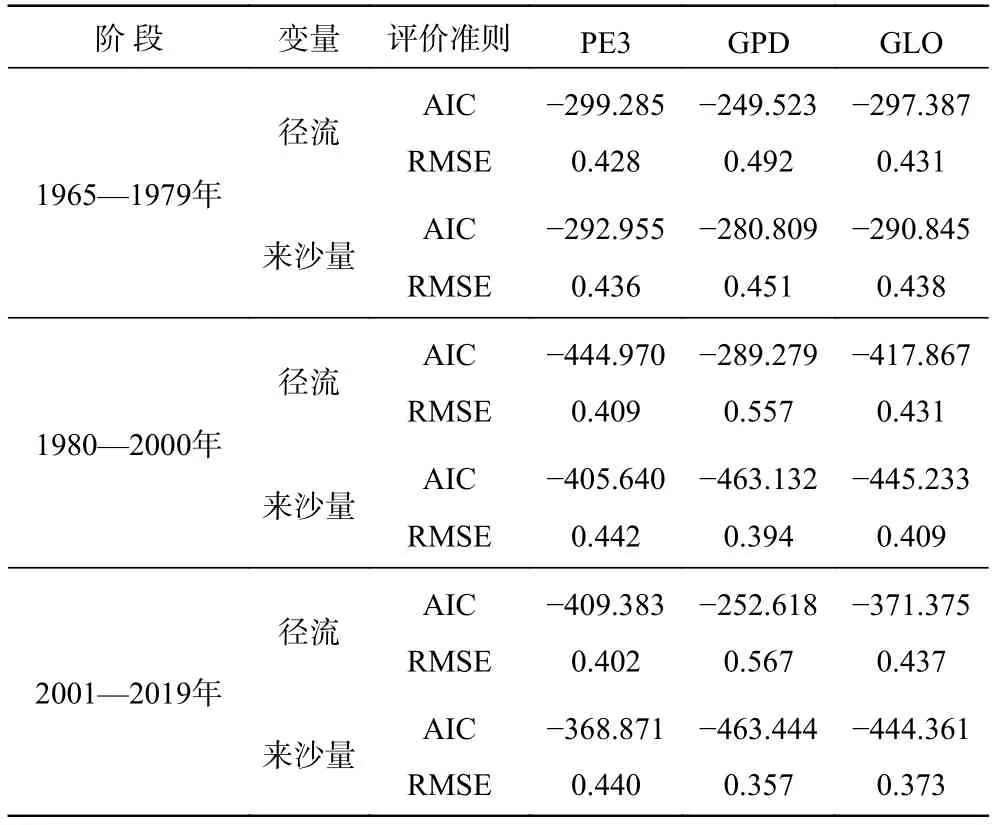
表3 水沙边缘分布选取Tab. 3 Selection of marginal distribution of runoff and sediment

表4是水沙联合分布模型优度评价计算结果，1965—1979 年阶段的Clayton 、1980—2000年阶段的Clayton及2001—2019年阶段的Frank对应的欧式距离d分别是0.045 7、0.045 6和0.052 6，为各阶段最小。因此水沙序列3个阶段的联合分布模型分别由Clayton、Clayton和Frank Copula函数来拟合。

表4 水沙联合模型选取Tab. 4 Selection of runoff-sediment joint model

根据Copula函数优度评价结果，3个阶段水沙组合的联合模型为式（6）~（8），由式（4）计算水沙组合不同序列的风险模型及联合(OR)重现期等值线见图4。图4为3个阶段在重现期水平100、50、20、10、5和2 a联合重现期等值线，同一个重现期对应着无数个水沙组合。不同重现期等值线分布较为规律，说明各阶段的水沙组合并未出现较大的波动。

图4 3个阶段水沙联合分布及联合重现期等值线Fig. 4 Joint runoff-sediment distribution and joint recurrence contours in three periods

对于1965—1979年，有：

对于1980—2000年，有：

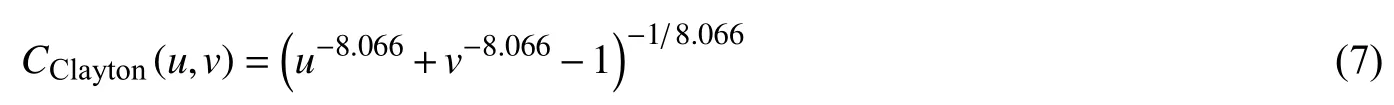
对于2001—2019年，有：

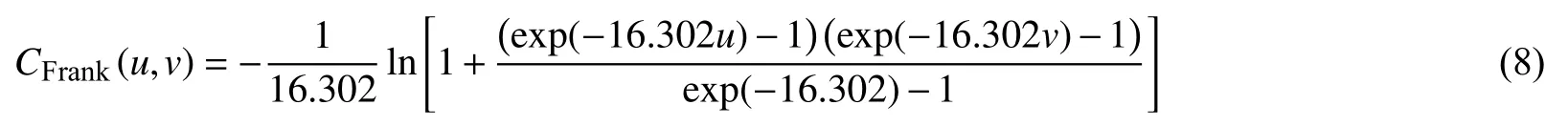
二变量水文分析中，各变量之间的变化是否具有一致性，反映了变量之间的相关关系。本文以pf=25%、pk=75%作为划分频率，将水沙概率分为丰、平、枯3种状态，9种不同组合方式[17]，对水沙组合的变化特征进行分析，计算结果如表5所示。从整体上看，3个不同序列的水沙同步频率分别为84.52%、84.40%和83.20%，要远大于水沙异步的频率，说明大通水文站水沙序列之间具有较强的相关性，但水沙同步概率在3个阶段依次减小也反映了人类活动对流域水沙一致性的影响在逐步扩大。在水沙同步频率中，水平沙平的占比较高（分别为42.26%、42.20%和41.60%），而水丰沙丰、水枯沙枯的比例则较为接近。其次，在水沙异步频率中，水丰沙枯（或水枯沙丰）的概率均为0，说明来水来沙条件维持在相对稳定的平衡状态，极端情况较少。

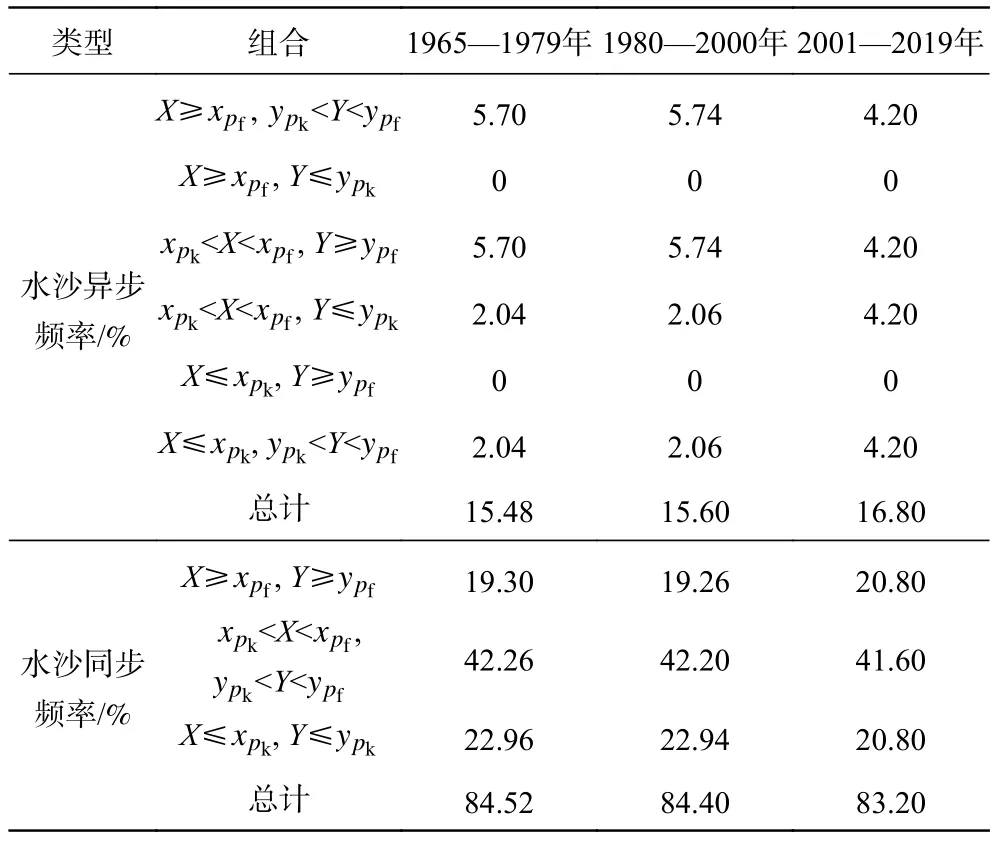
表5 大通水文站水沙丰枯遭遇计算Tab. 5 Calculation of flood and drought of runoff and sediment at Datong Hydrological Station

4.2 边缘函数选取不确定性分析

多变量水文分析中，导致结果不确定性的主要原因有两方面：一是由于样本实测数据长度不够，导致样本容量代表总体时出现偏差；二是模型函数的选取及函数参数的确定[18]。本文开展了针对边缘分布函数选取的不确定性分析，分别计算了联合重现期为20 a条件下每个序列不同边缘分布对应的1 000组最可能组合，进行边缘函数选取不确定性分析，结果如图5和表6所示。

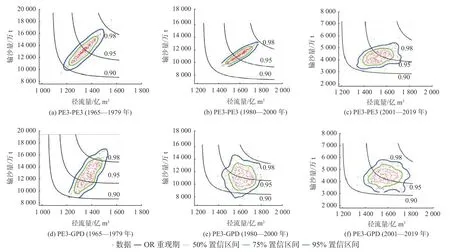
图5 3个阶段不同边缘分布组合对应的50%、75%和95%置信区间面积Fig. 5 Areas of 50%, 75%, and 95% confidence intervals for different combinations of marginal distributions in three periods

由图5可以看出1965—1979年和1980—2000年阶段的PE3-PE3组合方式对应的最可能组合相对集中，因此置信区域呈细长型，其他4个则呈椭圆形，6种情况下的95%置信区间均跨越了各自对应的10 a和20 a联合重现期等值线。从表6计算结果可以发现，不同的边缘分布组合条件下，Copula函数参数θ的变化幅度不大；对比3个序列的95%置信区间面积可以发现，采用PE3-PE3组合方式对应的置信区间面积明显小于PE3-GPD组合的置信区间面积，说明在本文中PE3- PE3边缘函数组合方式可以减少函数选取的不确定性。

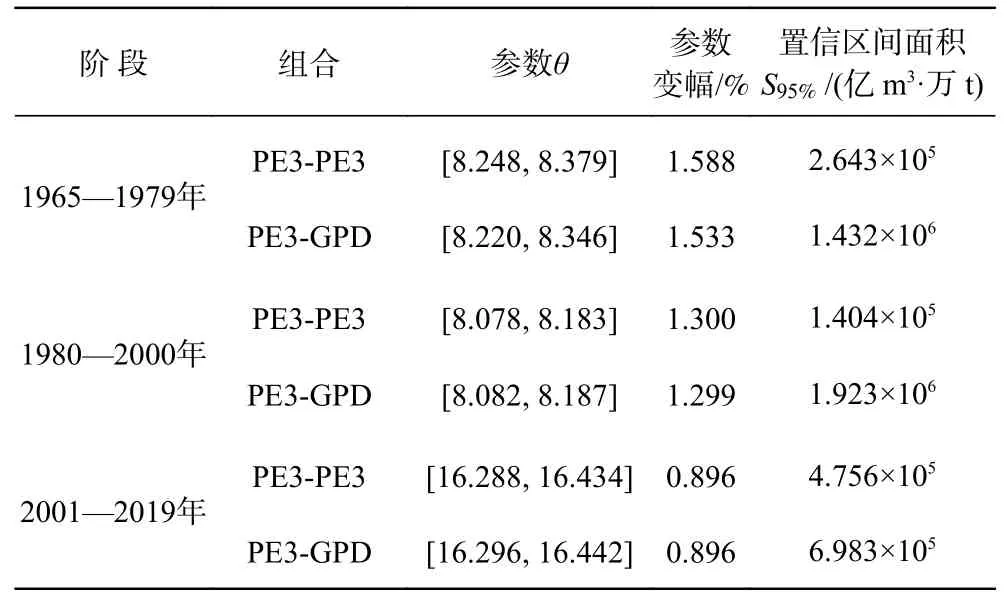
表6 边缘分布选取不确定性评价指标的95%置信区间取值Tab. 6 Values of 95% confidence interval of uncertainty evaluation index selected by marginal distribution

5 结 语

本文基于大通水文站1965—2019年的逐月径流量与来沙量资料，采用滑动Copula函数对水沙联合序列进行变异分析，通过对分段序列进行Copula函数建模，分析水沙变异的一致性，并对各段序列的边缘函数选取进行不确定性分析研究，得出主要结论如下：

（1）大通水文站多年水沙序列关系变异发生在1979年和2000年。1965—2019年间径流量和输沙量均呈减小趋势；相比1965—1979年阶段，1980—2000年间水沙变化波动出现不一致现象；2000年后径流量和输沙量减少趋势较为明显，其中输沙量减少达200%以上。

（2）1965—1979年、1980—2000年和2001—2019年3段序列的最优Copula函数模型分别是Clayton、Clayton和Frank Copula。水沙丰枯一致性计算结果表明，大通水文站多年水沙序列同步频率分别是84.52%、84.40%和83.20%，远大于异步频率，反映了大通站水沙序列具有较强的一致性。

（3）边缘分布函数选取不确定性分析表明，采用PE3-PE3边缘函数的组合方式的95%置信区间远小于采用PE3-GPD组合的置信区间面积，说明在本文中PE3-PE3边缘函数组合方式可以减少函数选取的不确定性。