基于改进模拟退火算法的软件可靠性模型参数估计方法
温晓玲,孙智孝,姜梦岑,艾笑天
(航空工业沈阳飞机设计研究所,辽宁 沈阳 110035)
软件可靠性可定义为在规定使用环境、规定时间下,不发生失效的概率[1],已成为最关键的软件质量属性之一。作为度量软件可靠性的重要途径,从20世纪70年代起,学术界提出许多与时间相关的软件可靠性评估模型,用于软件可靠性评估和预测工作[2]。
目前,现有软件可靠性增长评估模型的参数估计多采用最大似然估计(Maximum Likelihood Estimation,MLE)方法[3]。但是MLE方法在很多非线性求解情况下很难得到最优的精确解,导致软件可靠性模型精度和质量受到较大约束。因此,许多学者开始对模型参数估计方法展开研究,以提升模型参数估计效率和精度[4-6]。其中,文献[4]采用遗传算法进行可靠性模型参数求解,但是该方法结构较为复杂且精确度较低。文献[5]采用和声搜索(Harmony Search,HS)算法进行可靠性模型参数求解,该方法更适用于高维复杂非线性方程求解算法的优化问题,应用于软件可靠性模型(属于一般非线性方程)的参数求解时,其搜索范围过大且收敛速度慢。文献[6]应用蚁群(Ant Colony Algorithm,AC)算法进行可靠性模型参数求解,具有解的全局性好、收敛速度快等优点。文献[7]应用狼群算法进行可靠性模型参数求解,在算法执行过程中需要加入先验知识来提高求解的精确度和优化参数搜索方向,即其依赖于先验知识获取的可信性。
近年来,模拟退火算法作为一种通用的随机搜索算法,已经被广泛地应用于各个领域的非线性求解问题[8-10]。与其他非线性求解算法相比,其具有适用于较大的搜索空间、快速收敛于一个可接受的优秀解、比穷举法更有效、不需要额外的先验知识等优点。因此,模拟退火算法已经被应用在基于支持向量机的软件可靠性模型参数选择问题中[11-12]。
本质上,软件可靠性模型参数求解也是一个局部搜索最优化问题,因此,本文考虑应用模拟退火算法开展软件可靠性模型参数估计研究。首先,基于模拟退火算法,提出相应的参数求解过程;然后,针对模型参数求解最优化问题,提出一种改进的模拟退火(Modified Simulated Annealing)算法,即结合软件可靠性模型特征,确定相应的惩罚函数,以提升算法收敛精度。在此基础上,提出一种基于改进模拟退火算法的软件可靠性模型参数估计方法(简称为MSAE法);最后,将MSAE法与MLE法、HS法和AC法应用于3组经典的软件可靠性模型和4种典型失效数据集中,开展工程实例研究。通过实例比较分析,验证了MSAE法在求解收敛进度和模型拟合性能改进方面的有效性。
1 基于模拟退火算法的参数求解过程
模拟退火算法借鉴了固体退火原理,即从某一较高初温出发,伴随温度参数的不断下降,结合概率变化特性,在目标可能的解集空间中随机寻找目标函数的全局最优解。因此,本文基于模拟退火算法,提出以下的模型参数求解过程。
① 依据当前解算结果,生成一个位于有效解集空间的新解算结果。本过程主要是对当前解算结果进行内容或结构上的变化,例如对解算结果的内容或结构进行交换或倒置,从而产生一个位于有效解集空间的新解算结果。这个新的解算结果由当前解算结果的结构与取值方式来决定,从而对冷却进度表的选取或生成产生影响。
② 计算当前解算结果与新解算结果所对应的目标函数之间的差值。本过程针对当前解算结果和新解算结果,分别计算对应的目标函数值。进而按照某种特定方法(例如增量计算等),计算两者对应目标函数之间的差值。
③ 判断新解是否被接受,判断的依据是一个接受准则。本过程依据某种接受准则,对新解算结果与当前解算结果的目标函数差值进行分析,判断其是否可被接受。较为经典的接受准则是Metropolis准则,若“目标函数差值”的导数值Δt′<0,则接受新解算结果作为当前的解算结果,否则以概率exp(-Δt′/T)接受新解算结果作为当前的解算结果。
④ 若确定新解算结果被接受,则用新解算结果替代当前解算结果。若依据Metropolis准则,以较高置信度的概率判定新解算结果被接受,则将当前解算结果替换为新解算结果。可将当前解算结果中对应的结构或内容替换为新解算结果。同时,对相应的目标函数进行完善。若当前新解算结果被接受,则意味着完成一次迭代,可以在新解算结果基础上开展新的分析;若当前新解算结果不被接受,则还需要在当前解算结果基础上开展新的分析。
2 基于改进模拟退火算法的软件可靠性模型参数估计
首先,在模拟退火算法基础上,结合软件可靠性模型参数的物理含义,提出改进的模拟退化算法,进而提出基于改进模拟退火算法的软件可靠性模型参数估计方法。
2.1 结合模型求解特征的改进模拟退火算法
考虑到软件可靠性模型各个参数的物理含义(例如,GO模型的参数a>0,b<1等),引入禁忌搜索,即不符合实际意义的参数,考虑给其评价函数(反映模型对失效数据的拟合性能,均方差函数MSE()即是一种典型的评价函数)一个非常大的惩罚函数P,即
(1)
式中:x1,x2,…,xm为模型参数变量;m为参数维数。此时,可以得到扩展评价函数为
S(x1,x2,…,xm)=λ1·MSE(x1,x2,…,xm)+λ2·P(x1,x2,…,xm)
(2)
式中:λ1为原始评价函数(即MSE函数)的权重系数;λ2为惩罚函数(即P函数)的权重系数。λ1、λ2有如下关系:
λ1+λ2=1,λ1>>λ2
(3)
通常可以取:

(4)
2.2 基于改进模拟退火算法的模型参数估计算法
基于上述改进退火算法,提出新的软件可靠性模型参数估计算法。MSAE法流程如图1所示。
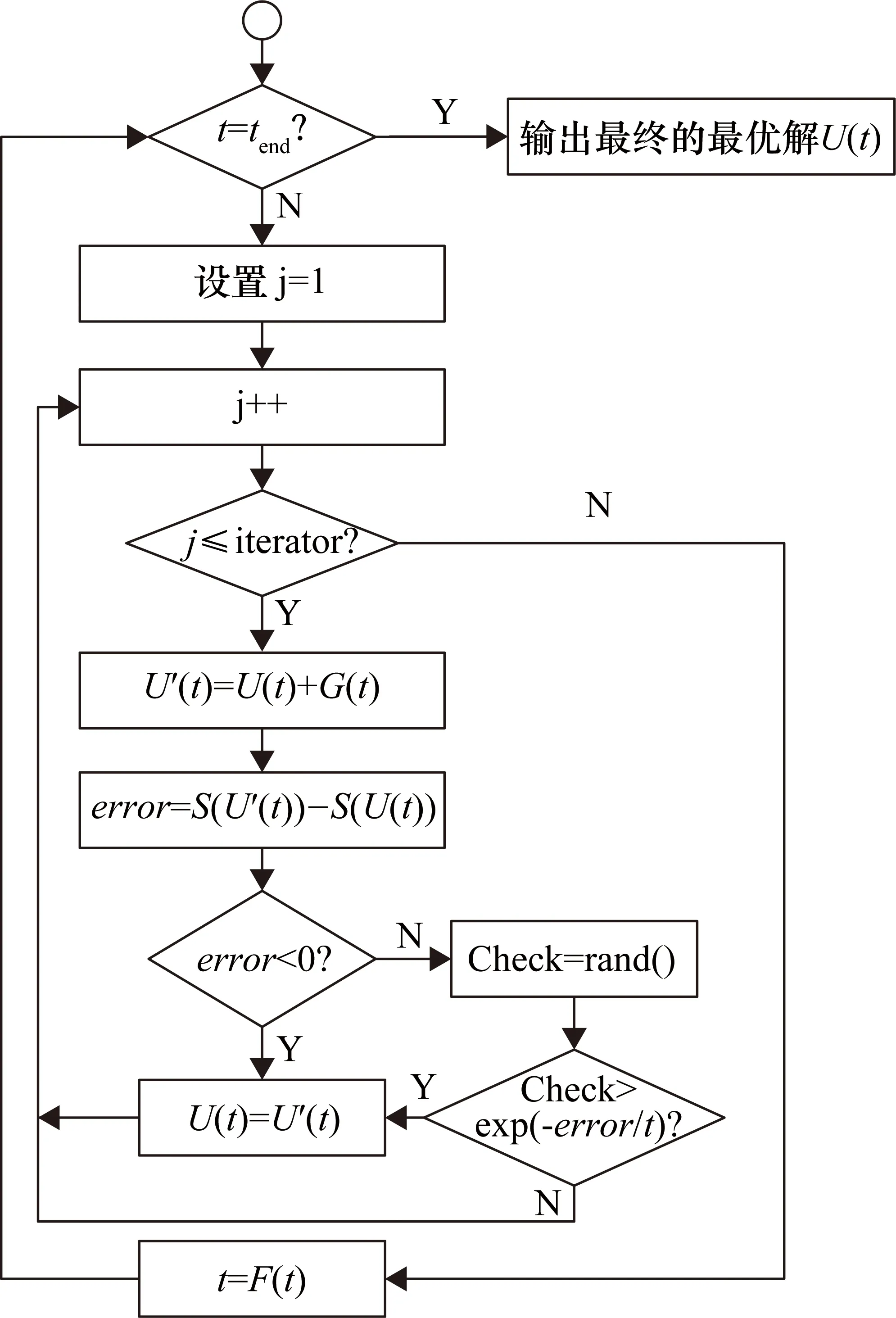
图1 MSAE算法流程图
依据图1,给出MSAE法如下。
① Input()://失效数据读入
N;//为软件失效数据量
M(t);//为软件失效间隔时间
② Init()://初始化
设置iterator,即邻域内的解数量;
③ while(t>tend)//t为退火过程中的温度
{
for(j=1;j<=iterator;j++)
{
随机生成U(t)邻域内的解U′(t)=U(t)+G(t);//G(x)为邻域选择函数
计算error=S(U′(t))-S(U(t));//S为评价函数
if(error<0)//新生成的解比较优
{
U(t)=U′(t);//完全接受为新解
}
else
{
Check=rand();//随机产生一个在[0,1]之内的数值
if(Check>exp(-error/t))
{
U(t)=U′(t);//也接受为最新解
}
}
}
t=F(t);//温度逐渐下降,对于不同温度采用不同的下降函数F(可根据模型参数特点,选择一个减函数作为下降函数F)
}
④ 重复上述步骤,直至t=tend
⑤ 输出最终的最优解U(t)
3 实例分析
验证试验采用了Sys3[12](19个数据)、Sys4[13](20个数据)、Sys5[1](60个数据)和Sys6[1](200个数据)共4组公开的经典失效数据集。这4组经典失效数据集分别来自Ohba[13]、Wood[14]、Lyu[1]等学者收集的经典软件可靠性失效数据(具体数据内容可参见相应文献),常用于软件可靠性模型拟合性能的比较和分析。借助拉普拉斯法,这4组数据的可靠性趋势均为“增长”,所适用的软件可靠性模型包括GO、MO、S型等增长评估模型[11]。
为验证所提出的方法的有效性,将本文提出的MSAE法和MLE法、HS法、AC法分别应用于GO、MO和S型这3个经典软件可靠性增长评估模型[14]。需要说明的是,蚁群算法与狼群算法均属于群体智能算法,相比较而言,蚁群算法更成熟且具有典型性,而狼群算法严重依赖于先验知识的可信性,所以本文选择蚁群算法作为群体智能算法代表参与实例分析验证。
采用不同方法对GO、MO、S型这3个模型的参数进行估计,并计算每个模型对失效数据集的拟合值(均方差值(MSE))。依据模型对失效数据的拟合程度,来验证本文提出的MSAE法的有效性和可行性。具体计算结果如表1~表4所示。
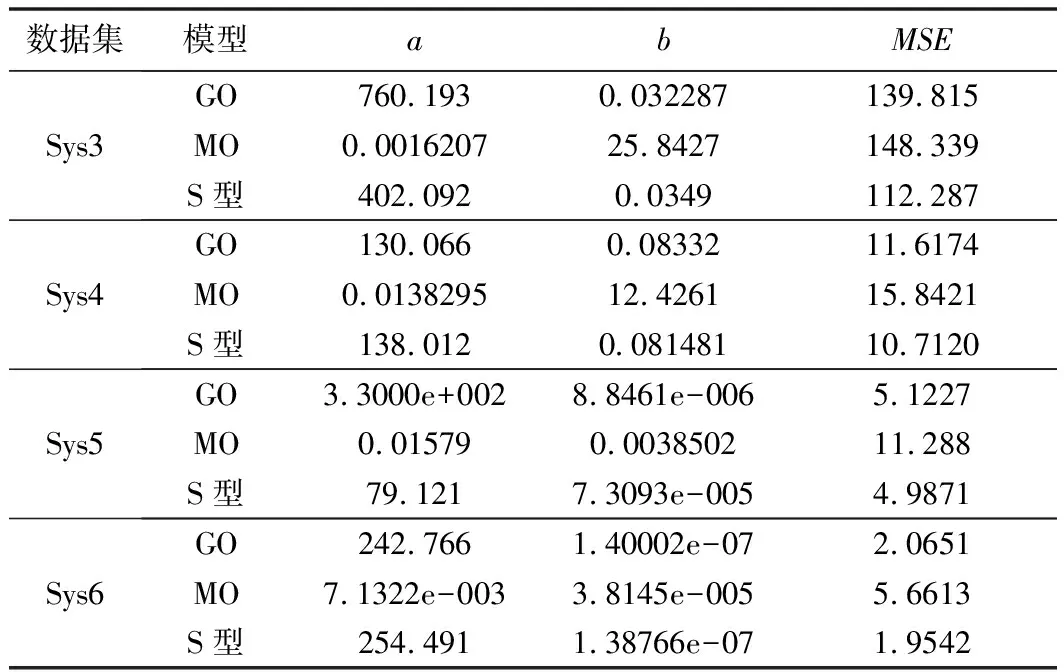
表1 模型在4组数据集上的拟合结果(基于MSAE法)
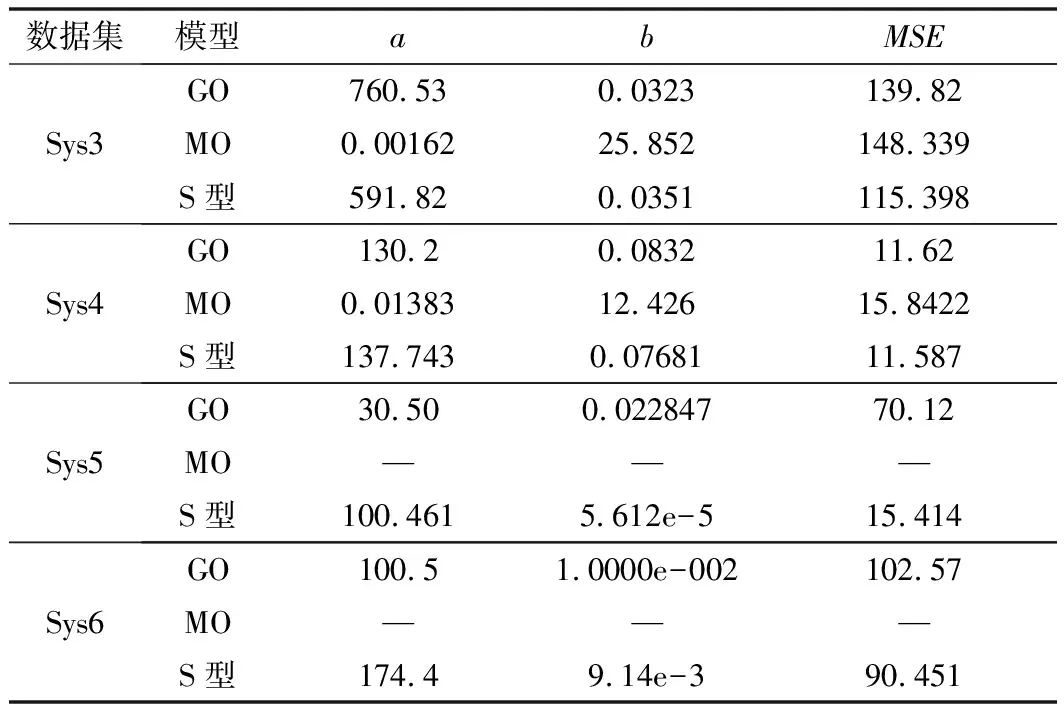
表2 模型在4组数集据上的拟合结果(基于MLE法)
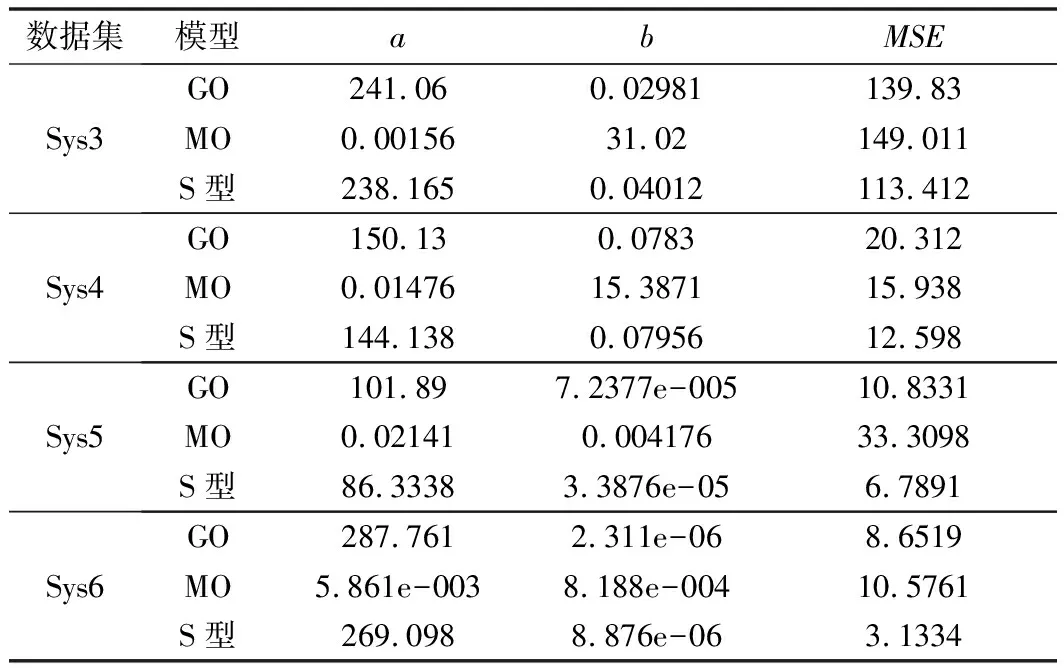
表3 模型在4组数据集上的拟合结果(基于HS法)
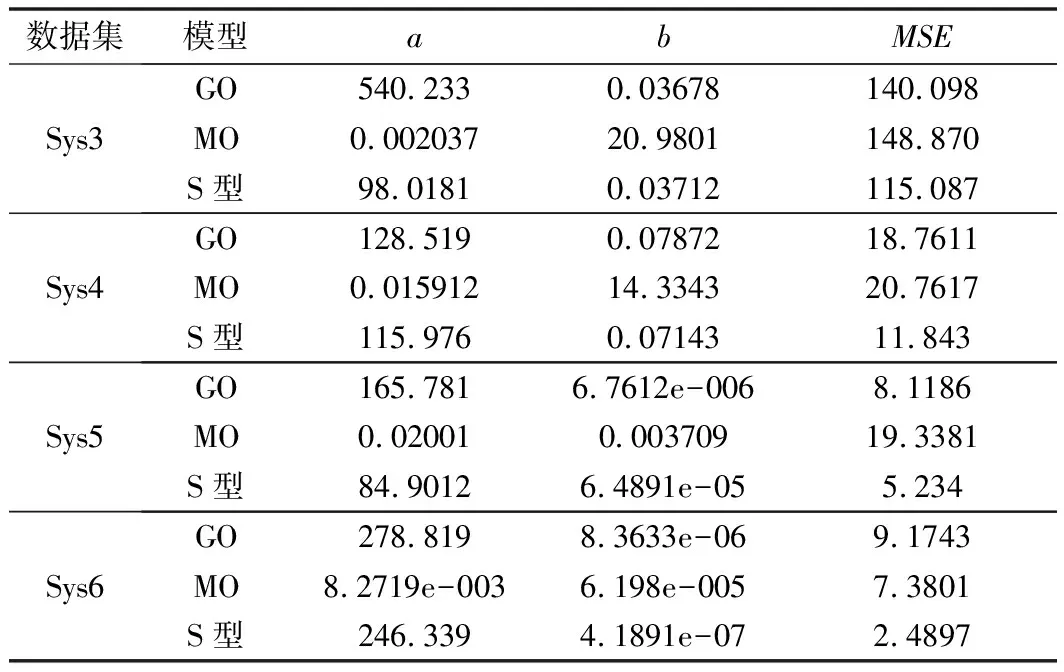
表4 模型在4组数据集上的拟合结果(基于AC法)
依据表1~表4中的数据进行对比分析,具体如下。
(1)针对小样本数据集Sys3和Sys4的对比分析。
在本文中,小样本数据集是指Sys3和Sys4(即失效数据量≤30个数据)。针对小样本数据集Sys3和Sys4,MSAE法、MLE法、HS法和AC法对模型参数求解的收敛情况基本一致,均能给出较为合理的参数估计值。此外,根据这4种方法计算出的失效数据的拟合值(MSE值)相差不大,即4种方法在3个模型中对小样本数据的拟合性能相差不大。例如,针对Sys3,基于MSAE法的GO模型的拟合值为139.815,而基于MLE法、HS法和AC法的GO模型的拟合值则分别为139.82、139.83、140.098。
由此可知,针对小样本失效数据集(Sys3和Sys4),这4种参数估计方法对模型参数求解的收敛情况基本一致,均能给出较为合理的参数估计值,同时基于MSAE法、MLE法、HS法和AC法的可靠性模型拟合性能相差不大。
(2)针对大样本数据集Sys5和Sys6的对比分析。
在本文中,大样本数据集是指Sys5和Sys6(即失效数据量≥60个数据)。在大样本数据集Sys5和Sys6上,MLE法在MO模型中存在参数求解不收敛的情况,即无法获得合理的参数估计值。而MSAE法则明显改善了在某些失效数据上MLE法参数求解不易于收敛的问题。此外,基于MSAE法的软件可靠性模型拟合值比MLE法、HS法和AC法要小。例如,针对Sys5,基于MSAE法的GO模型拟合值为5.1227,而基于MLE法、HS法和AC法的GO模型拟合值分别为70.12、10.8331和8.1186;针对Sys6,基于MSAE法的GO模型拟合值为2.0651,而基于MLE法、HS法和AC法的GO模型拟合值分别为102.57、8.6519和9.1743。
由此可知,针对大样本失效数据集(Sys5和Sys6),基于MSAE法的软件可靠性模型参数求解收敛效果要优于MLE法;同时,基于MSAE的模型拟合性能要优于MLE法、HS法和AC法。
通过图2~图5进一步阐述了基于MSAE法的GO模型和MO模型对数据集Sys5和Sys6的拟合效果。
从图2~图5可以看出,基于MSAE法的GO模型和MO模型对Sys5和Sys6的拟合效果也非常良好,即模型曲线与原始数据非常接近。

图2 GO模型对Sys5的拟合(基于MSAE法)

图3 MO模型对Sys5的拟合(基于MSAE法)

图4 GO模型对Sys6的拟合(基于MSAE法)
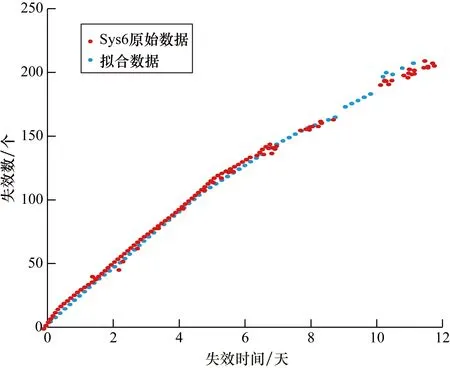
图5 MO模型对Sys6的拟合(基于MSAE法)
依据上述分析可知,MSAE法相比于传统的MLE法,可以有效提升软件可靠性模型的拟合性能,即MSAE法具有可行性和有效性。
4 结论
本文在模拟退火算法基础上,结合软件可靠性模型求解的最优化问题,提出一种改进模拟退火算法,即结合软件可靠性模型特征,确定相应的惩罚函数。依据改进模拟退火算法,提出了一种新的软件可靠性模型参数估计方法(MSAE法)。最后,在4组数据集上,将MSAE法与MLE法、HS法和AC法应用于GO、MO和S型这3种经典软件可靠性模型,开展工程实例研究,实例验证结果表明:
① 在指定的小样本数据集Sys3和Sys4上(即失效数据量≤30个数据),MSAE法与MLE法、HS法和AC法的参数求解收敛效果基本一致。且基于MSAE法、MLE法、HS法和AC法的软件可靠性模型对失效数据的拟合性能相差不大。
② 在指定的大样本数据集Sys5和Sys6上(即失效数据量≥60个数据),MSAE法可有效改善基于MLE法模型参数求解不易于收敛的问题。同时,基于MSAE法的软件可靠性模型对失效数据的拟合性能优于MLE法、HS法和AC法。
③ 基于实例分析结果可以得出初步的结论,即MSAE法、HS法和AC法在指定的小样本和大样本数据集上都较为适用,而MLE法则更适用于小样本数据集(即失效数据量≤30个数据)。
在未来的工作中,还需要在更多的失效数据集上比较分析MSAE法、MLE法、HS法和AC法的拟合性能,进一步判定这几种典型算法的适用性范围。

