基于分子动力学模拟的超低温SiO2 材料开裂影响因素分析
吕世明,沈才华,郭 丹,陈 伟,李雪松,唐 凯
(1.保利长大海外工程有限公司,广东 广州 510623;2.河海大学 岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098)
1 前 言
分子动力学(molecular dynamic,MD)是一种非常重要、应用广泛的分子模拟方法[1]。该方法通过分子间作用力改变分子的坐标和动量,得到整个体系的动力学信息[2]。早在1957年,Alder和Wainwright[3]采用分子动力学方法来研究气体和液体的状态方程,此后,学者们开展了大量的分子动力学研究工作。1995年,Plimpton[4]证明了分子动力学并行运算的高效性,开发了功能强大的分子动力学软件LAMMPS(large-scale atomic molecular massively parallel simulator),该软件目前广泛用于各领域。Zhou等[5]采用分子动力学模拟方法对裂纹扩展过程进行了研究,结果表明裂纹在扩展初期扩展速度快速增大,最后达到稳定。Holland等[6]利用分子动力学软件对Si的裂纹尖端扩展速度和能通量进行了比较。Huang等[7]用Pearson,MEAM 和Tersoff势函数分别对SiC中的缺陷点或簇的形成能以及迁移能进行研究。国内采用该研究方法逐渐增多,但对岩石的研究较少。何满潮等[8]采用分子动力学法研究高岭石在不同温度下拉伸力学性能的温度效应。孙晓庆[9]对在不同的系统温度、加载速率的条件下Si中裂纹扩展进行分子动力学模拟计算。孟筠青等[10]运用分子动力学模拟法,构建了包含7 000 个赵庄煤大分子的基体仿真模型,模拟结果与试验结果较为吻合。分子动力学中势函数是核心,因此陈强等[11]对常用势函数进行了归类总结评价。LJ势函数应用最广[12],但主要用于惰性气体或液相转变的分子模拟研究[13]。郭宗标等[14]基于Tersoff势函数研究了SiC 沿着固定三个方向的初始裂纹的扩展力学行为。岩石作为一种天然材料,内部存在大量微裂纹损伤,采用分子动力学方法研究原生裂纹的扩展以及在不同状态下的变化过程,对于研究岩体的失稳破坏具有重要意义。
2 基于微观裂纹模型的建立
LAMMPS是一款开源软件,免费而且功能强大,可以很好的模拟材料分子尺度的力学行为,但目前针对岩石材料的研究很少,主要原因是目前没有与之一一对应的、应用成熟的势函数可以使用,所以本研究针对岩石的主要组成成分SiO2,建立了分析岩石基材的裂纹扩展微观机理研究的方法。
2.1 势函数与模型
势函数根据多体作用的复杂程度可分为对势和多体势,SiO2其分子结构的研究相对较多,普遍认为采用多体势模拟较合适,常用的多体势有Feuston-Garofalini(FG)势、Vashishta、Vessal 等。本 实 验SiO2的模拟采用由两体势和三体势组成的Vashishta势函数[15],表达式为:

Vashishta势函数的参数表见表1。

表1 Si-O-O 参数表[15]Table 1 Si-O-O parameter table[15]
使用VMD 软件的建立SiO2模型(其中SiO2分子构型见图1),建模方法见图2,试样尺寸为x×y×z=199.16Å×99.56Å×6.948Å。

图1 二氧化硅空间构型 (a)分子构型;(b)空间构型Fig.1 Spatial configuration of silica(a)molecular configuration;(b)spatial configuration

图2 计算模型示意图 (a)SiO2 模型示意图;(b)模型实例Fig.2 Schematic diagram of calculation model (a)schematic diagram of silica model;(b)model examples
3 不同影响因素作用下对裂纹扩展行为的影响
3.1 加载速率对裂纹扩展行为的影响
微正则系综(NVE系综),在10 K 温度下,研究了加载速率分别为10Å/ps和1Å/ps时,对Ⅰ型裂纹扩展行为的影响。图3(a)显示:当加载速率为10Å/ps时,作用一段时间后,空位形成。图3(b)显示:继续作用一段时间后预制裂纹尖端和空位两个不同位置分别形成一个新的裂纹尖端,称为“裂纹1(即预制裂纹扩展的裂纹尖端crack tip)”和“裂纹2(即空位vacancy)”,随着载荷能量的进一步传播,在两个裂纹尖端形成能量重分布的“竞争”态势,最终裂纹1先开始起裂,裂尖1被拉开,从而产生能量释放并影响裂纹2周围能量场,这可能会抑制裂纹2的扩展使得裂纹最终沿着裂尖1向前扩展。

图3 加载速率为10Å/ps裂纹扩展行为 (a)空位形成;(b)裂纹沿裂纹尖端扩展Fig.3 Crack growth behavior at a loading rate of 10Å/ps (a)vacancy formation;(b)crack propagates along the crack tip
当加载速率为1Å/ps时,从图4(a)可以看出,初始裂纹尖端出现空位,但在低加载速率下裂纹并未沿着空位扩展,而是从裂纹尖端向前扩展,原因是虽然空位处原子间结合能较低,但慢速加载导致原子有充足的时间重新调整位置,降低势能,提高整体稳定性,空位得到填充,导致裂纹沿尖端扩展。

图4 加载速率为1Å/ps裂纹扩展行为 (a)空位形成;(b)裂纹沿裂纹尖端扩展Fig.4 Crack growth behavior at loading rate of 1Å/ps (a)vacancy formation;(b)crack propagates along the crack tip
如图5所示,图2(a)中圆2区域在裂纹扩展后能量变化稍低于圆1、3区域,裂纹穿过圆2区域用时也较长,该区域原子有更多的时间调整位置,降低势能,提高稳定性,所以圆2区域最后总能量偏低。总体势能、动能,A 区域平均应力以及总体温度的变化与加载速率为10Å/ps时的计算结果规律基本相同,但模拟发现加载速率会引发裂纹扩展路径的变化,这与试验结果基本一致。

图5 加载速率对裂纹扩展的影响 (a)不同加载速率圆1能量变化;(b)不同加载速率圆2能量变化;(c)不同加载速率圆3能量变化;(d)不同加载速率系统总能量变化;(e)A 区域平均应力变化;(f)系统温度变化Fig.5 Effect of loading rate on crack growth (a)energy change of circle 1 under different loading rates;(b)energy change of circle 1 under different loading rates;(c)energy change of circle 3 under different loading rates,(d)total energy change of the system with different loading rates;(e)change of average stress in area A;(f)system temperature change
3.2 力加载对裂纹扩展行为的影响
NVE系综,10 K 温度下,将图2(a)中速度加载换成力加载,并将圆2、3 位置进行调整,调整后如图6(a)所示。应力采用维里应力计算方法,如式(4)所示:

式中:V为需要计算应力部分的体积;i,j为原子i周围的j原 子;r iα,r jα为i原 子 和j原 子 在α方 向 的 位置;f ijβ为β方向j原子对i原子的力;m i为i原子的质量;v iα和v iβ为i原子在α和β方向的速度。
调整加载力的大小,当加载应力<1.793 GPa时,裂纹不扩展;当加载应力≥1.793 GPa时,裂纹扩展。初始裂纹长度为9.5Å,根据式(5)和式(6)可计算出起裂应力强度因子与裂纹扩展驱动力:

力加载计算的裂纹扩展应力强度因子比速度加载情况下大4.9倍,裂纹扩展驱动力增大了24倍。裂纹一旦开裂,迅速扩展,由于裂纹扩展速度过快,而且是端部加载,导致模型纵向断裂,如图6(d)所示,究其原因,是圆2、3部分的水平应力大于竖直应力(图6(f),(g));断裂后,断裂的部分受力快速运动,因此系统温度急剧升高,系统动能也急剧升高,如图6(h)、(i)所示。

图6 力加载对裂纹扩展行为的影响 (a)力加载模型示意图;(b)裂纹沿裂纹尖端扩展(5 ps);(c)纵向起裂(25 ps);(d)纵向裂纹扩展(26 ps);(e)圆1水平应力与竖直应力;(f)圆2水平应力与竖直应力;(g)圆3水平应力与竖直应力;(h)温度变化;(i)动能、势能、总能量变化;(j)三个圆区域能量变化Fig.6 Effect of force loading on crack growth behavior (a)schematic diagram of force loading model;(b)crack propagation along crack tip(5 ps);(c)longitudinal crack initiation(25 ps);(d)longitudinal crack growth(26 ps);(e)horizontal stress and vertical stress of circle 1;(f)horizontal stress and vertical stress of circle 2;(g)horizontal stress and vertical stress of circle 3;(h)temperature change;(i)change of kinetic energy,potential energy and total energy;(j)energy change of three circular regions
力加载方式显示,当力小于某阈值时,微裂纹不会扩展,所以理论上脆裂蠕变变形不会发生,这与岩石力学的长期强度理论基本一致,但数值模拟的计算裂纹起裂应力远大于长期强度值,主要是因为数值模拟的是微观的、完整的分子结构应力状态。本研究模拟的微观裂纹未考虑实际岩石微环境存在缺陷的影响,而现实中,岩石暴露在空气中,岩石裂纹尖端含有水或者电离的羟基OHˉ,SiO2的Si—O键与之发生反应,见式(7):


图7 应力腐蚀下的G-R 曲线Fig.7 G-R curves under stress corrosion
3.3 不同温度下力加载对裂纹扩展行为的影响
NVE系综下,对平均加载应力1.793 GPa的系统温度设置分别为1、2、3 K,研究力加载情况下,温度对裂纹扩展行为的影响。如图8(a)~(c)所示,对比这三个裂纹扩展的行为,发现1、3 K 温度下,沿着+y方向分叉的裂纹位置在沿着ˉy方向分叉裂纹的左边,2 K温度下,二者的位置相反。三个裂纹扩展均表现出初始慢,之后越来越快的特点,水平向裂纹最终分叉导致裂纹不再沿着+x方向扩展。不同温度下,水平裂纹的最终扩展长度和平均扩展速率如图8(d)、(e)所示。从图可见,不论裂纹最终扩展长度还是平均扩展速率,从1 K 到3 K 均是增加。

图8 不同温度下力加载裂纹扩展行为 (a)1 K 温度下裂纹扩展行为;(b)2 K 温度下裂纹扩展行为;(c)3K 温度下裂纹扩展行为;(d)温度与裂纹总长的关系;(e)温度与裂纹平均扩展速率的关系Fig.8 Crack growth behavior under force loading at different temperatures (a)crack growth behavior at 1 K;(b)crack growth behavior at 2 K;(c)crack growth behavior at 3 K;(d)relationship between temperature and crack length;(e)relationship between temperature and average crack growth rate
由此可见,力加载作用下,裂纹扩展行为不仅与力的大小有关,还与温度有关,温度影响原子运动,从而影响势函数,原子之间作用力改变,裂纹扩展行为随之改变。
3.4 模型厚度对裂纹扩展行为的影响
NVE 系综下,温度为10 K,初始裂纹长度为10Å,加载速度为10Å/ps,模型厚度由6.948Å 增大到34.74Å,对模型厚度变化影响进行研究,结果发现,模型厚度会改变裂纹扩展行为。从图9(a)、(b)可以看出在扩展的最后阶段,裂纹尖端偏离了原来的方向,有一层原子“粘”在下表面,裂纹沿着新的表面扩展,分析认为产生这一现象的原因主要是裂纹尖端始终自洽寻找断裂韧度或者扩展阻力小的地方扩展,厚度方向的增加使裂纹扩展过程中裂纹尖端的“弱键”增加,使得扩展行为发生了细微的变化。从图9(d)可以看出,厚度增加后,裂纹扩展过程A 区域(见图6(a))平均拉应力增加。厚度增加后,系统内原子数量增加,所以系统动能势能和总能量变化均增大,裂纹扩展形成的表面增大(图9(c)),扩展后三个圆区域内能量增幅变大,如图9(e~g)所示。假设裂纹形状系数不变时,模型厚度增大的同时也导致开裂过程中所需应力强度因子计算值增大(图9(h)),分析认为这是由裂纹厚度与分子结构的相对尺度大小决定的,即厚度与分子结构尺度相当时,存在宏观力学上的尺度效应,此时的裂纹形状系数理论上应该不同。
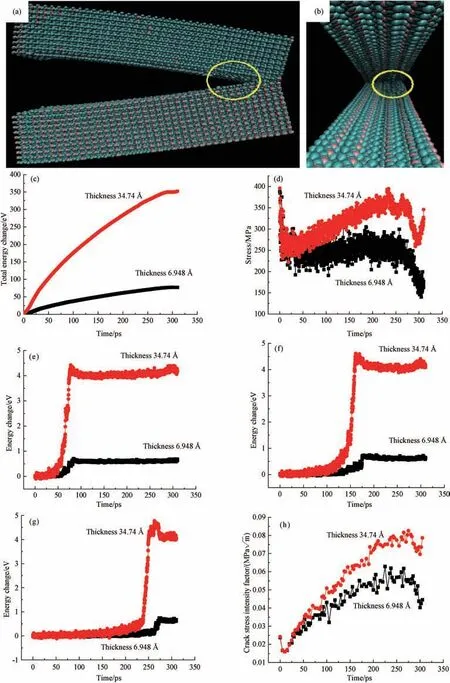
图9 不同厚度裂纹扩展行为 (a)模型正视图;(b)模型左视图;(c)系统能量变化;(d)A 区域应力变化;(e)不同厚度圆1能量变化;(f)不同厚度圆2能量变化;(g)不同厚度圆3能量变化;(h)不同厚度应力强度因子计算值Fig.9 Crack growth behavior of different thickness (a)model front view;(b)left view of the model;(c)system energy change;(d)stress change in area A;(e)energy change of circle 1 with different thickness;(f)energy change of circle 2 with different thickness;(g)energy change of circle 3 with different thickness;(h)calculated values of stress intensity factors for different thickness
4 结 论
采用分子动力学模拟技术可以很好的模拟分析加载速率、力加载方式、不同温度下力加载方式及模型厚度对裂纹扩展行为的微观影响规律,对揭示固体材料的裂纹扩展微观机理和探究裂纹控制技术具有重要理论指导意义。通过对超低温SiO2脆性材料的裂纹扩展规律研究得出如下主要结论:
1.加载速率会引发裂纹扩展路径的变化。力加载方式显示,力小于某阈值时,微裂纹不会扩展,数值模拟的计算裂纹起裂应力远大于实际岩石的长期强度值,主要是由于实际岩石存在缺陷并受到复杂环境因素的影响。
2.由于温度影响原子运动,从而影响势函数,原子之间作用力改变,裂纹扩展行为随之改变,表现出裂纹总长和裂纹平均扩展速率随温度的增加而增加。
3.裂纹模型厚度增加后,系统内原子数量增加,所以系统动能、势能和总能量变化均增大。裂纹扩展形成表面增大,扩展后三个圆区域内能量增幅变大,模型厚度增大的同时导致开裂过程中所需平均应力强度因子计算值增大,这主要是由假设的裂纹形状系数不变不符合实际情况导致,总体上模拟的计算结果和裂纹扩展规律基本合理。
分子动力学模拟技术为探究岩石类工程材料的脆裂蠕变微裂纹扩展机理提供了一种有效途径,当然目前势函数的选择和参数的确定具有一定经验性,对不同分子结构和不同环境下势函数选择的研究还有待进一步深入。

