基于CEEMD与SVM的离心泵转子不对中故障诊断方法研究

肖幸鑫，宋礼威，张翊勋，董 亮，张宇航

（1.江苏大学 流体机械工程技术研究中心，江苏镇江 212000；2.中广核工程有限公司 核电监控技术与装备国家重点实验室，广东深圳 518172）

0 引言

离心泵作为在各类工程中常用的机械设备，广泛应用于例如石油，煤矿等能源的开采；排水灌溉等农业生产方向；航空航天航海等领域，占到泵产品总量的70%［1］。在实际工程应用中，离心泵的转子故障成为了困扰国内外相关研究人员的难题［2］；判断离心泵是否发生故障，主要依靠离心泵在运行过程中出现异常的噪声与振动［3］。

离心泵转子不对中故障主要由转子间存在高度差或转子间存在距离引起的，如图1所示。

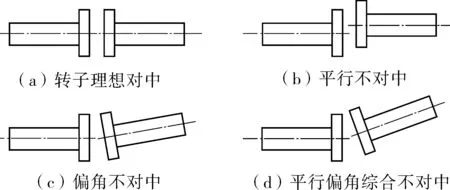
图1 典型的不对中故障Fig.1 Typical misalignment fault

2018年李峰等［5］提出了基于电机电流时频特征的不对中故障诊断方法，有效地提高了识别转子系统的轴系不对中故障的正确率，因此通过提取信号时频特征参数，用于故障诊断是有效的；唐贵基等［6］提出一种谱峭度与变分模态分解的转子故障诊断方法，解决了在噪声环境下转子微弱不对中故障特征难以提取的问题，刘忠等［7］提出一种IVMD算法，并将其应用到离心泵空化声发射信号特征提取，因此模态分解算法广泛用于特征提取中，降低故障特征参数提取的难度；XIE等［8］将不对中故障的特征参数离散和模糊化构造故障决策表，能够有效地诊断汽轮发电机组转子不对中故障；YAO等［9］提出了基于分段阈值小波去噪、经验模态分解、遗传算法和最小二乘支持向量机的混合铁路滚动轴承故障诊断方法；肖军等［10］针对往复压缩机气阀故障，将气阀振动信号不同频段的能量作为故障特征，提出了结合模糊C均值聚类和支持向量机的二叉树多分类诊断方法。

小波分析与经验模态分解（empirical moded ecomposition，简称EMD）系列方法作为信号处理的常见方法，小波分析在提取故障特征信息时需要选择合适的小波基，不同的小波基对于故障特征信息的提取影响巨大，在使用小波分析时必须进行多次试验来确定最合适的小波基，并且确定后不能更改，对信号不具备自适应性；而EMD克服了基函数无法自适应的问题，可以将一段信号进行固定模式开始分解，从高频至低频拆分成若干个IMF分量。转子不对中故障主要故障频率位于低频，因此使用EMD作为转子不对中故障信号处理方法能够更有效地提取故障特征［11］。SVM作为有监督算法的典型算法之一，利用给定的训练数据集进行训练学习从而得到函数模型，并根据函数模型预测新数据类型，王金东等［12］将EMD信息熵和支持向量机（SVM）结合应用于往复式压缩机的轴承故障诊断，发现该方法能够准确识别压缩机轴承故障；杜星洲［13］提出了基于振动信号与SVM的旋转机械故障诊断研究方法，利用SVM对旋转机械的常见故障进行分类和识别；而无监督算法对于样本数据类型未知，主要依靠数据间的相似性对数据进行分类，黄惠中［14］利用聚类分析为基础，构建了包含信号处理与特征提取及特征选择技术在内的智能故障诊断模型；李志国等［15］针对潜水磨碎泵流道堵塞的故障诊断，提出了一种基于奇异值分解和固有时间尺度分解的电流信号分析和构建支持向量机故障识别模型相结合的方法。

本文主要是针对离心泵转子不对中故障与正常状态区分，是一个二分类问题，而SVM作为一个二分类模型相较于其他神经网络模型具有较大的优势。本文利用互补经验模态分解（CEEMD）对电涡流位移传感器采集的振动位移信号进行分解，通过相关系数法与阈值选取有效IMF分量，通过重构有效IMF分量，通过提取重构后信号中的时域故障特征参数组成特征向量，再将该特征向量输入SVM中进行转子不对中故障判断。

1 互补集合经验模态分解

EMD在处理非平稳及非线性数据上，具有非常明显的优势，适合于分析非线性、非平稳信号序列［16］，具有很高的信噪比。

CEEMD算法相较于EMD在故障特征提取中存在模态混叠问题和集中经验模态分解（ensemble empirical mode decomposition，简称EEMD）存在运算量大，计算效率低的问题，CEEMD算法具备迭代次数少，计算成本低，诊断精度高等优点［17-20］。

1.1 CCEMD基本原理

CEEMD主要计算步骤如下：

（1）向原始信号s（t）中不同的正负白噪声x（t）：

xna（t）、xnb（t）分别为加入正负白噪声后的信号，其中n为正整数，由此可以得到2n组IMF集合。

（2）将得到的2n组IMF集合中的每个IMF分量使用EMD进行分解，每个信号都可以得到一组IMF，将第i个信号的第j个IMF分量记为Cij。

（3）将得到的2n组IMF进行平均，从而得到最终的IMF分量。

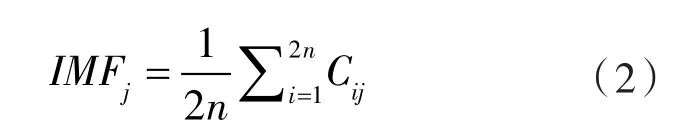
该算法需要相较于EMD需要添加2个参数：辅助白噪声幅值k和对数N，一般当N取100时，k 取 0.01～0.10［21］。

1.2 相关系数法分析

基于CEEMD的分解流程，可以知道从原信号分解的IMF中提取有效的IMF，是实现转子不对中故障诊断的重要步骤。采用相关系数法，提取出与原信号高于阈值的有效IMF分量来重构信号，对重构后的信号进行时域特征提取。

设信号采样信号数为M，原始信号为S，第k个IMF分量为IMFk，则IMF分量与原信号相关系数的计算式为：

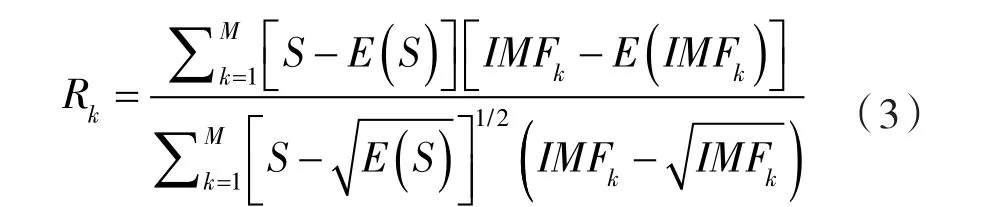
式中 Rk——相关系数；

E ——平均。

阈值TH定义为相关系数的标准差，计算式为：

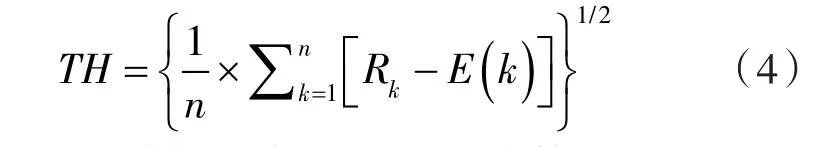
式中 n ——分解出来的IMF的个数。

2 时域故障特征提取

时域信息是以时间为变量描绘出信号的波形，时域信号包括有量纲特征参数与无量纲特征参数，本文选用平均值和均方根、峭度、波形因子、峰值因子、脉动因子、裕度因子7个时域特征参数进行分析［17］。时域特征参数公式见表1。表1中，Ns表示采样点数，i=1～Ns；x（i）表示采集点数中第i个信号。

表1 时域特征参数公式Tab.1 Time domain formula

3 SVM原理

SVM是一类按监督学习方式对数据进行二元分类的广义线性分类器，主要功能是解决模式识别区域的数据分类等问题，在解决小样本、非线性及高维模式识别问题中具有特有的优势，基本原理在文献［22-23］中有详细描述。本文中不再赘述。

4 转子角不对中故障试验

为了模拟离心泵角不对中故障，搭建离心泵故障模拟实验台，其主要设备包括卧式离心泵，三相异步电动机，电磁流量计，电涡流振动位移传感器等。在试验中离心泵转速通过变频电机调节控制，系统流量通过出口阀门进行调节，离心泵转子不对中故障通过在联轴器放置垫片来模拟实现。

试验使用的电涡流振动位移传感器参数见表2，利用电涡流振动位移传感器采集转子振动位移信号，采样频率为25 600 Hz，离心泵的额定转速为2 900 r/min，额定流量为10.6 m3/h。

表2 电涡流传感器参数Tab.2 Eddy current sensor parameters

本次实验采集离心泵在同一流量下转速比分别为0.7n，0.85n，1.0n的工况，正常运转状态下的振动位移信号和转子角不对中故障振动位移信号；采集在同一转速下，流量比分别为0.7q，0.85q，1.0q工况下的正常状态下的振动信号和角不对中故障振动信号。

试验主要针对转子不对中故障中的角不对中故障进行研究，如图2，3所示，在电机端添加垫片来模拟实际工程中转子角不对中故障的发生，利用百分表测量联轴器位置的偏移距离来判断是否故障为转子角不对中。进行多次测量后，求得平均值记录见表3。

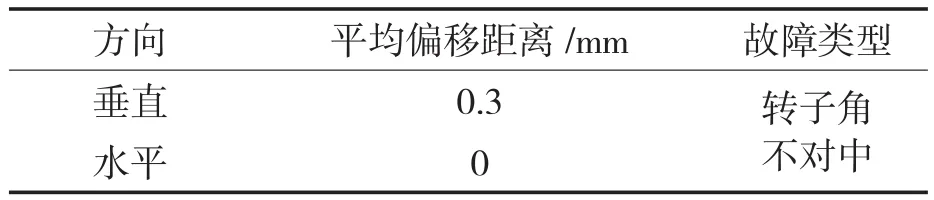
表3 联轴器偏移距离Tab.3 Coupling offset distance

图2 垂直方向偏移距离Fig.2 Vertical offset distance

图3 水平方向偏移距离Fig.3 Horizontal offset distance

5 试验数据分析以及验证

本文试验使用16通道采集卡，采集频率为25 600 Hz，采集时间为1 s，每组试验采集样本个数为 25 600个；选取2 900 r/min，10.6 m3/h工况下其中10 240个样本点绘制原始数据时域波形，如图4，5所示。

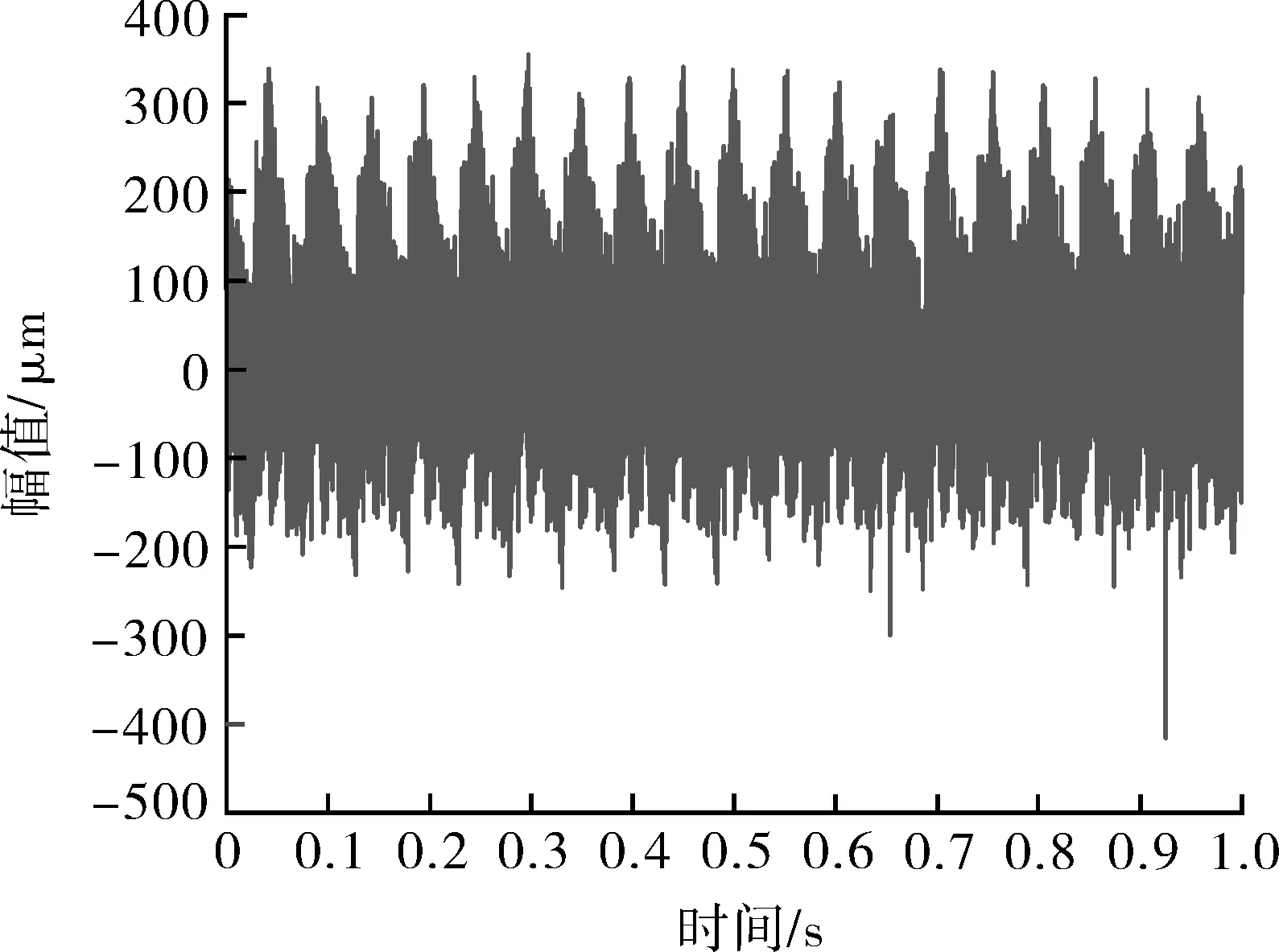
图4 正常工况时域Fig.4 Time domain diagram of normal working conditions

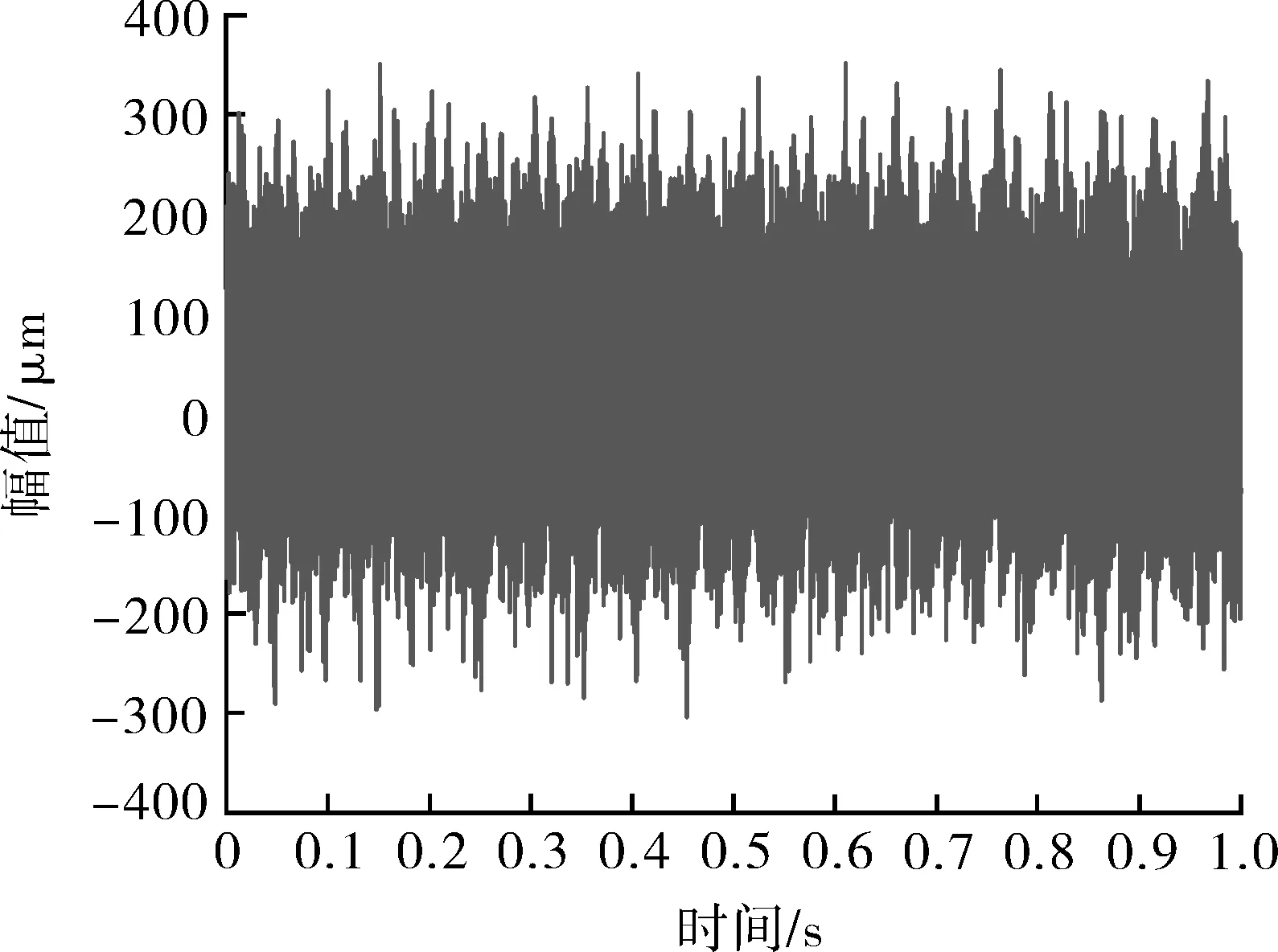
图5 故障工况时域Fig.5 Time domain diagram of fault working conditions

图6示出了正常工况与故障工况频谱对比，其中f'/f为倍频，f'为不同工况的实际频率，f是额定转速下对应的基频（48.33 Hz），实验中通过对工常工况以及故障工况在额定转速，额定流量下的频谱图进行分析可以发现，正常工况下的主频出现在1APF，故障工况下的1APF为主频，但是2APF的振幅明显增大，符合转子角不对中故障发生时的特征。

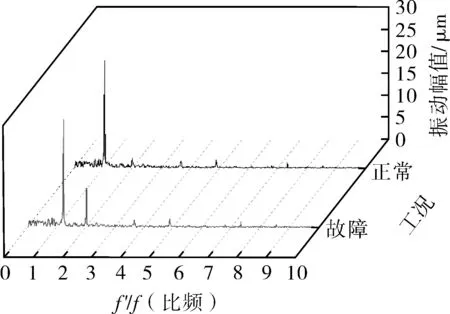
图6 正常工况与故障工况频谱对比Fig.7 Spectrum comparison between normal working conditions and fault working conditions

5.1 CEEMD分解以及信号重构

对正常工况下的额定转速，额定流量下的信号进行CEEMD分解，我们选取一组数据，数据点个数为2 560个，结果如图7所示。

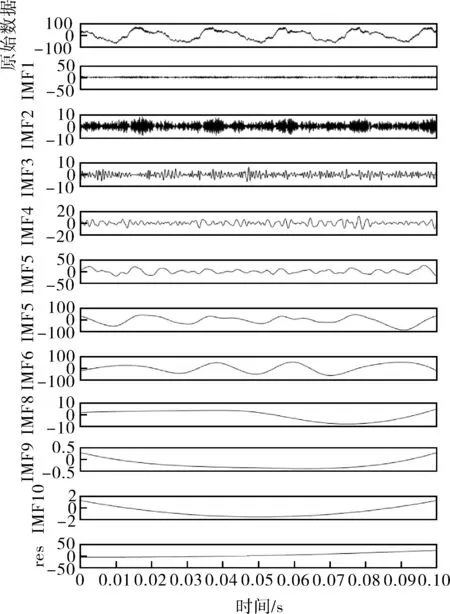
图7 CEEMD分解Fig.7 CEEMD decomposition diagram

各IMF分量与原信号的相关系数见表4，为了方便表示，各相关系数均乘以100%。得到相关系数后，利用式（4）可以计算出阈值TH=18.18%，因此选取有效 IMF 分量为 IMF1，IMF2，IMF6，IMF7，进行信号重构，从而得到一个新的信号NewIMF，NewIMF的时域波形如图8所示。

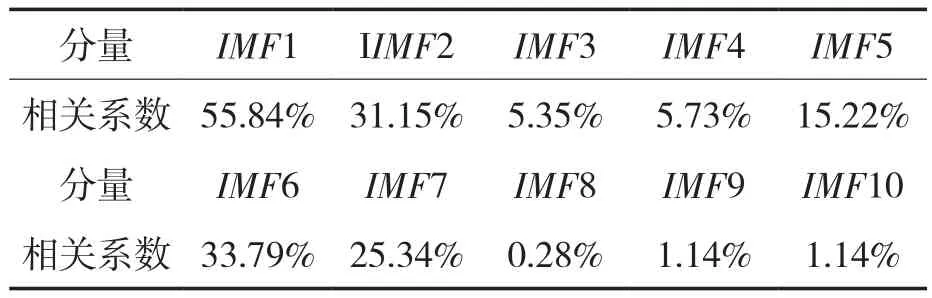
表4 相关系数Tab.4 Correlation coefficient

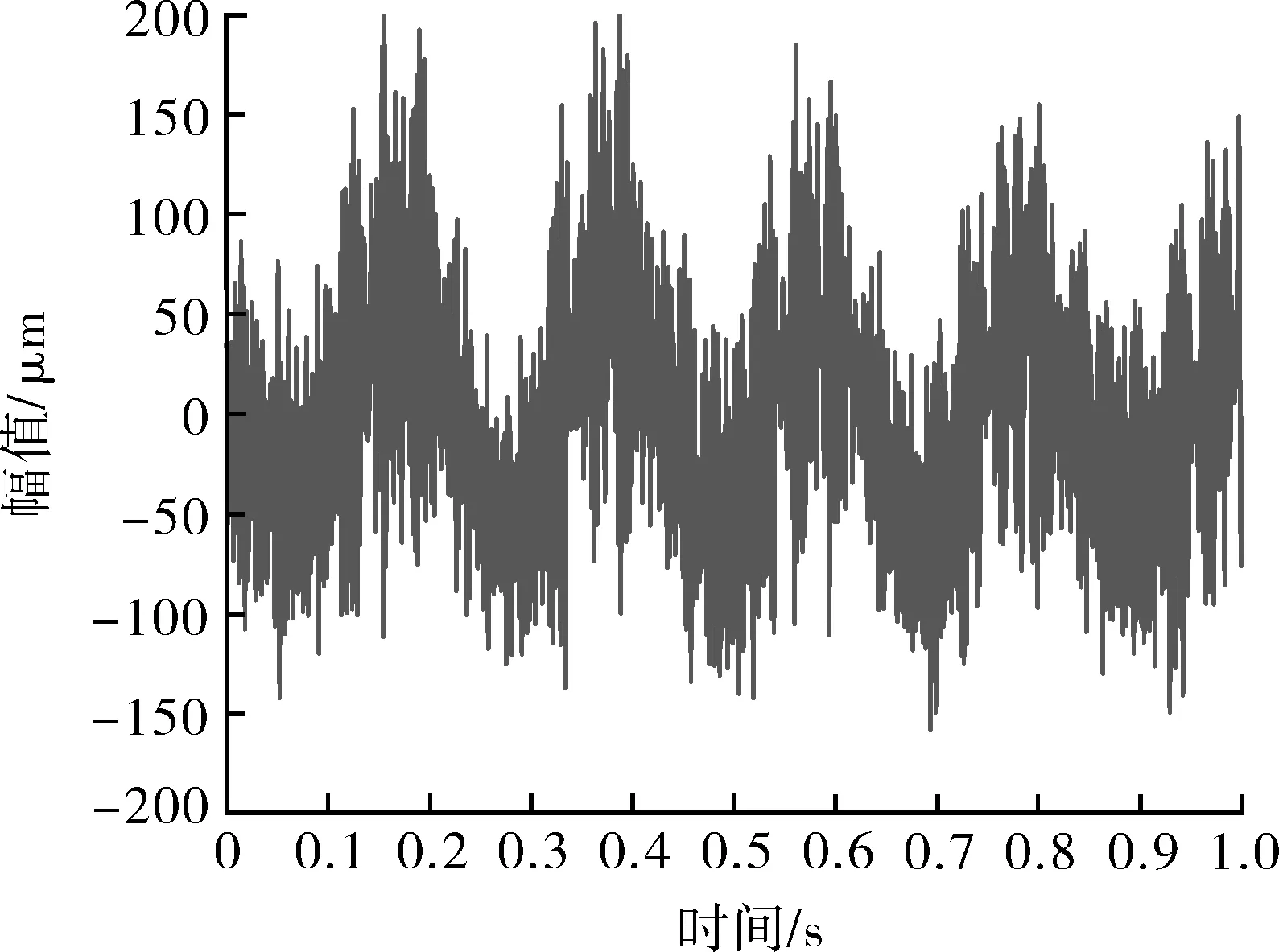
图8 重构后NewIMF信号Fig.8 Reconstructed NewIMF signal

5.2 故障特征提取

选取离心泵正常运行状态信号，离心泵泵转子角不对中故障状态信号各50组，一共100组信号，每组2 560个数据点，对每组信号都进行上述方法分析，通过重构后信号，得到平均值和均方根2个有量纲时域特征参数以及峭度、波形因子、峰值因子、脉动因子、裕度因子5个无量纲时域特征参数，并对特征参数进行min-max归一化处理使数据映射至［-1，1］区间内：

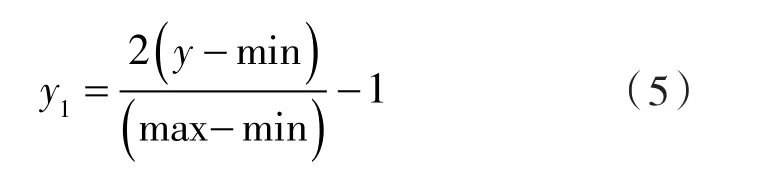
式中 y1——归一化后数据；

y ——原始样本数据；

min ——样本数据最小值；

max ——样本数据最大值。

归一化处理后组成特征向量，由于篇幅原因表中仅列出正常状态下和故障状态下各10组特征向量见表5。

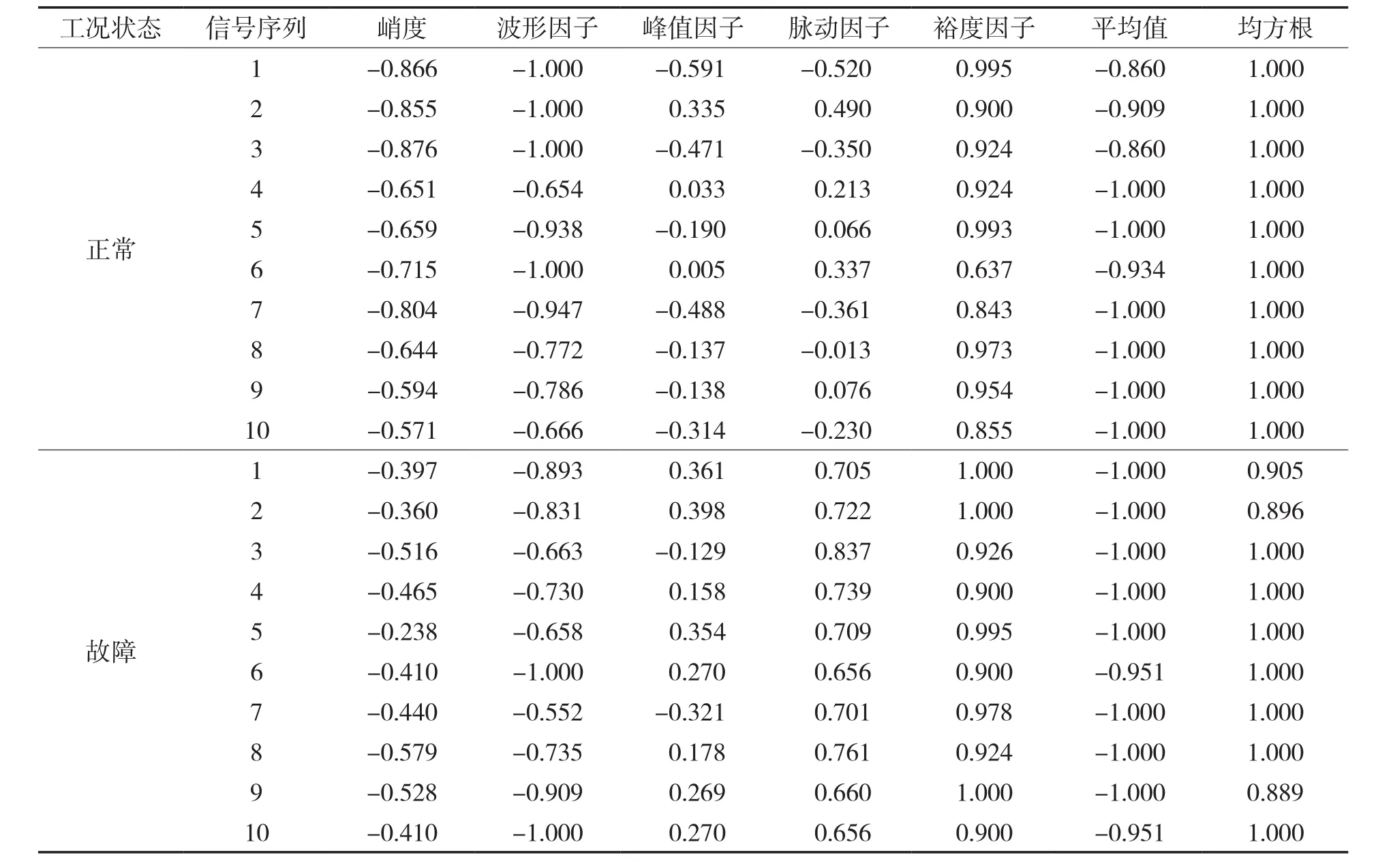
表5 部分正常与故障特征向量Tab.5 Part of the normal and fault characteristic vectors

5.3 利用SVM进行故障识别

支持向量机选用RBF作为核函数，利用交叉验证法选用最合适的惩罚系数c和参数g，在数据集中随机选择80组数据，作为训练集，20组数据作为测试集。由于是随机选择数据作为训练集以及测试集，为了避免识别误差，因此进行20次识别，并取其平均值，由表可知平均值为93%。图9示出第一次识别结果，将识别结果记录见表6。

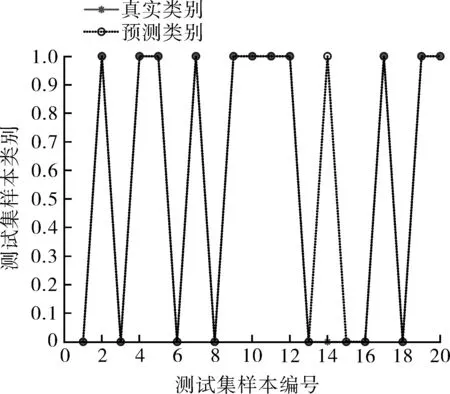
图9 第一次SVM故障识别结果Fig.9 Identification results of the first SVM fault

表6 SVM识别结果Tab.6 Identification results of SVM

6 结论

（1）离心泵转子不对中故障发生时，转子振动信号的时域特征参数会发生变化，且在频谱中二倍频会明显增大。

（2）使用CEEMD算法进行信号分解，采用相关系数法和阈值能够有效的选择出包含故障特征的IMF分量。

（3）对重构后的故障信号提取时域特征参数，组成特征向量输入SVM中，可有效的识别出离心泵转子不对中故障，并具有较高的准确率。