菲涅尔衍射及有限时域差分在光栅仿真中的应用研究
宫鹏,徐桂成,张斯特,刘震宇
(中国科学院长春光学精密机械与物理研究所,长春 130031)
计算机技术的高速发展,为波动光学及电磁学方程的研究提供了数值解法的工具,也使得数值仿真方法在许多光学领域得到了广泛而深远的应用,从电磁学最基本的麦克斯韦方程组出发的有限时域差分方法,到光线传播的角谱理论和傅里叶光学,都可以用数值方法加以求解[1]。针对理论的光学公式在数值计算过程和实际研究中的实现技巧及应用等有许多成果,例如在超分辨率时光场经过结构后的高精度聚焦情况研究[2];在激光谐振腔的设计工作中腔内光束经过多次反射后的光场分布研究[3];角谱衍射公式及快速傅里叶变换在数字全息波面重建中的研究[4];在菲涅尔衍射计算中引入虚拟光波场以提高空间分辨率的研究[5];以及通过矩阵法改进光场传输算法以提高计算效率的研究等[6]。
基于波动光学衍射原理所设计的衍射光学元件在诸多领域中同样有着广泛的应用,如实现光束的整形[7],实现光束聚焦[8-9],产生衍射图样等[10-11]。光栅作为一种应用非常广泛的光学元件,在衍射光学尺度下的设计及制造需要较高的精度,其衍射场分布规律也随光栅几何的复杂程度增加而增加,因此光栅衍射场的仿真研究对于实际的光栅设计及加工具有深刻的指导意义。
本文从周期结构的相位光栅仿真分析出发,以菲涅尔衍射公式作为出射光栅之后光场传播的主要计算工具,辅以光栅区域的有限时域差分计算仿真,研究了一种系统的光栅仿真方法。在光的波长尺度内,有限时域差分算法的网格尺寸不能大于波长的,否则会导致计算精度的缺失,而在面对光栅尺寸较大或者需要计算的传播距离较远时,单独应用有限时域差分法会产生极大的计算量,也需要花费大量计算时间。因此在菲涅尔衍射的近场区,采取将有限时域差分计算得到的光场数据导出,用菲涅尔衍射公式来解决光场在后续介质中的传播问题,大大减小了计算量和计算时间。结果显示,光线在经过相位光栅后,在接收屏处产生了三个强度较高及对比度较高的衍射峰,即产生了可供后续处理及测量的光信号。同样的,在周期结构的光栅基础上,对于几何分布不规则的非等距光栅和有加工误差的光栅,也可以通过有限时域差分计算求解光栅区域内的光场分布,之后通过菲涅尔衍射解决光场在近场内的传播问题。
1 算法分析
根据惠更斯-菲涅尔公式在近似条件下得到的二维菲涅尔衍射公式解析形式的表达式为:
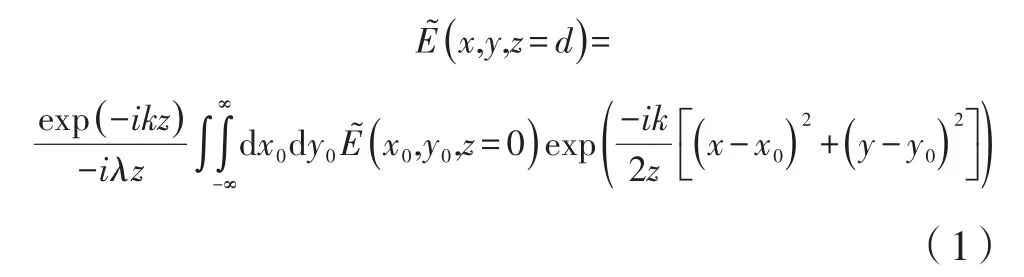
式中,定义光场出射面所在z坐标为0;光场经过传播后到达的接收屏位置所在z坐标为d,即为两屏之间距离;͂为复数形式表达的光场分布信息;为出射面处的几何坐标及对应位置的光场信息;为光场经过z=d距离传播后的接收屏位置处的几何坐标和对应的光场信息,即为所要求的经过传播后的光场信息;λ 为入射光线的波长;k=2π /λ 为对应波长光线的波数。解析形式的菲涅尔衍射公式针对接收屏处的各个位置,通过对出射面处的二维光场进行x和y方向的积分来得到整个出射面的光场对接收屏处各个位置的叠加效果。公式(1)中的积分上下限为-∞~+∞,当出射面处的通光孔径几何确定后,积分上下限即为实际的几何空间。整个模型的几何关系如图1所示。

图1 菲涅尔衍射模型分布示意图
将上面的解析形式的菲涅尔衍射公式进行离散化处理,得到:
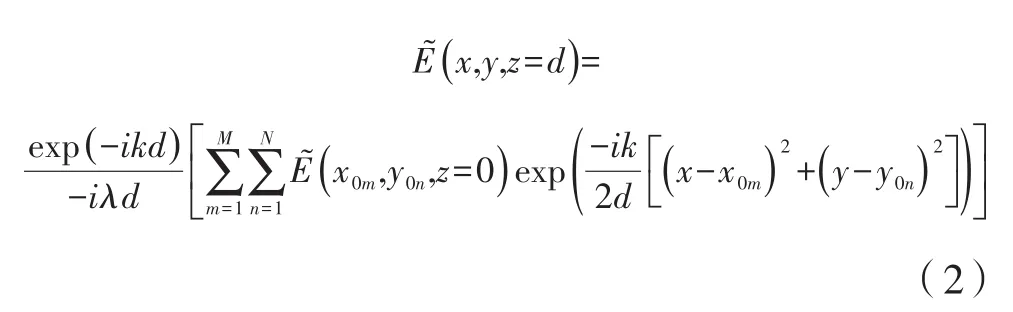
式中,M、N为将几何x、y方向离散化的单元数。
当所研究的问题为一维问题时,则上述的解析形式和离散形式的菲涅尔衍射公式化为如下的形式:

2 光栅仿真
常见的光栅类型包括幅值光栅和相位光栅。本文以相位光栅为例,首先运用有限时域差分方法计算光栅及光线入射区域的光场分布,之后在光栅出射面处导出光场分布数据,然后运用菲涅尔衍射公式对相位光栅进行仿真模拟。整个计算的流程如图2所示。
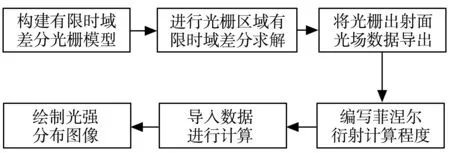
图2 光栅仿真流程示意图
这里的相位光栅设计为周期性结构,每个周期具有相同的栅距及占空比,光栅尺寸及相关材料属性如表1所示,几何模型如图3所示。

表1 相位光栅相关参数
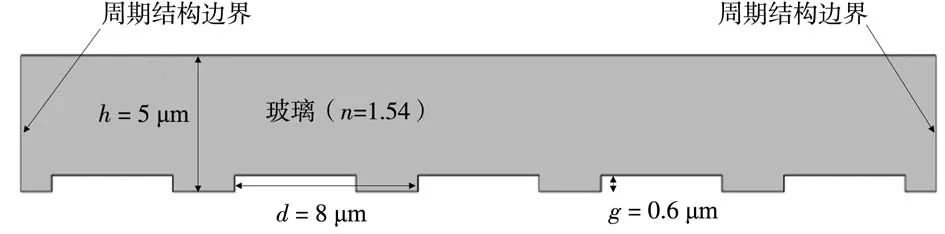
图3 相位光栅几何模型及相关参数
菲涅尔衍射公式所应用的条件为需要给出出射面的光场分布数据,无法直接应用于从空气入射到光栅即介质材料发生变化时光栅对光场的作用效果,而有限时域差分方法则可以处理介质变化区域的计算问题,因此结合波动光学的有限时域差分来计算光栅附近区域内的光场分布情况。之后通过导出光栅出射面处的光场分布数据作为后续步骤的原始数据,再利用菲涅尔衍射算法计算光场经过一定距离传播之后的分布情况,来仿真整个过程中光线经过光栅的作用之后在近场菲涅尔衍射距离下的分布结果。
首先进行有限时域差分部分的光栅仿真,模型如图4所示,这里面内方向为x、y坐标,面外方向为z坐标。通过设置两边的边界为重复性的周期边界条件,可以通过计算五个光栅周期来实现无限长的周期性结构的光栅衍射效果。在空气的边界处设置入射边界条件,入射光波的设置条件列于表2中。

图4 光栅有限时域差分计算模型

表2 有限时域差分入射光波设置
五个周期的光栅结构计算区域内的光场模的分布如图5所示,出射边界处的电场z方向分布图像如图6所示。

图5 光栅区域有限时域差分计算光场模结果图

图6 光栅出射面处光场z方向分布结果图
将出射边界处的电场z分量数据导出,后续研究即为光线射出光栅之后在空气中传播的过程中的衍射和干涉效应在接收屏处产生的光斑分布情况。
在实际制造及应用的光栅中,光栅都具有一定的宽度,通常有数百个周期,因此在上述有限时域差分计算得到的五个周期的出射光场数据基础上,需要根据光栅的周期结构特性将五个周期数据通过复制扩展至200个周期来模拟实际尺寸下的光栅结构。
根据菲涅尔衍射的条件,在算法计算中设置接收屏距出射面的距离为50 mm,接收屏上的观察宽度设置为-15~15 mm,图7为经过菲涅尔衍射算法计算得到的接收屏处的光场模的平方的图像,即为光强分布的图像,也对应实验上的光斑亮度。由计算结果图像可见,最终在接收屏上的光强分布主要集中在五个区域,其中0级衍射级和±1级衍射级强度最高,对比度较高,光斑亮度也最高,这三级即可作为光线经过光栅作用后产生的信号,通过后续的元件作用和信号采集即可进行设计和应用。
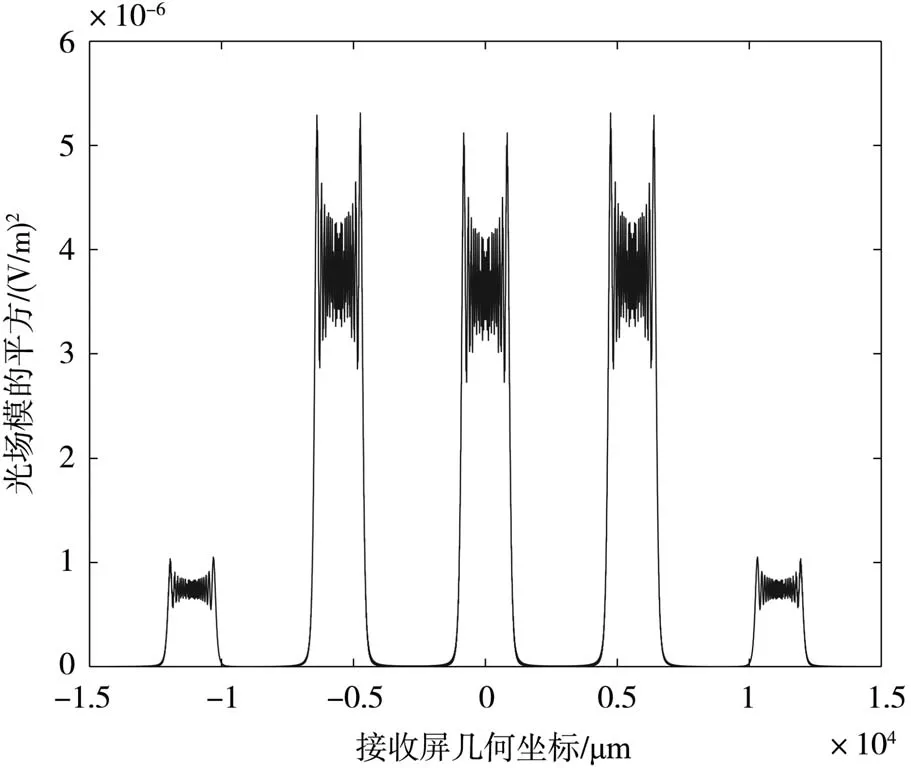
图7 接收屏处光场模的平方结果图像
3 结论
本文主要是基于菲涅尔衍射公式和电磁场的有限时域差分算法进行光栅仿真的分析。有限时域差分算法通过直接求解麦克斯韦方程组来解得光场的精确分布形式,但是缺点是对于网格尺寸的要求很高,通常要小于入射光波长的,因此当光栅所需要的计算区域较大或者需要计算的传播距离较远时,就会导致划分的网格数量极大,进而导致整个有限时域差分的计算过程花费时间过长。因此采用菲涅尔衍射与有限时域差分计算相结合的方式,首先通过有限时域差分方法构建模型求解得到介质过渡区域的光场分布,然后将计算得到的光栅出射面的数据导出,利用菲涅尔衍射公式编程计算得到光场在近场距离内也就是菲涅尔衍射区内的传播之后的分布情况,有效地解决了传播距离较远时有限时域差分计算量过大的问题和介质过渡区域的计算方法问题。基于以上研究步骤,本文构建了周期结构的相位光栅,通过设置有限时域差分模型的初始边界条件及将其数据结果进行扩展,使其与实际的光栅结构相匹配,之后将光场数据用于菲涅尔衍射计算。最终结果显示光线经过相位光栅的作用后在接收屏处共形成了五个衍射峰,其中0级和±1级衍射峰较强,对比度较高,可作为光信号供后续元件和设备的处理和采集。而且基于有限时域差分算法的通用性,对于几何结构不规律的非等距光栅和有制造误差的光栅,以上仿真方法同样适用,具有普适性。

