一种多约束条件下再入飞行器下沉式轨迹规划方法
张敏刚,杨 丁,刘 明,刘建辉,张宁宁
(空间物理重点实验室,北京,100076)
0 引 言
再入飞行器是一种具有特殊的大升阻比气动外形的无动力飞行器,能够在高度20~100 km 临近空域内高速度、远航程、长时间的机动飞行,其以高机动、强突防和操纵性强等特性著称。与传统惯性飞行器不同,再入飞行器依靠气动力控制、大横侧向机动飞行,可实现飞行器的指定轨迹规划飞行任务,可显著提高飞行器的环境生存能力。本文研究的重点内容是考虑复杂多约束条件下(力、热、位置、速度、方位角等约束条件)的一种下沉式轨迹规划技术,尤其是轨迹快速计算、机动轨迹生成以及优化策略研究。
目前轨迹规划设计主要集中在特定飞行任务下多约束的飞行剖面设计,具体针对指定射程、速度、高度、弹道倾角等约束的轨迹设计技术。传统的滑翔轨迹设计方法主要分为两类:a)通过建立飞行轨迹参数化模型,根据具体飞行任务,利用寻优算法迭代求解飞行器程序姿态角,但由于再入飞行器轨迹参数化模型高度非线性,迭代收敛慢,寻优效率低,此类方法通常仅适用于离线轨迹设计;b)利用平衡滑翔条件对原运动模型进行简化,建立飞行轨迹与飞行器受力之间的直接解析关系实现轨迹快速设计,但此方法较难满足弹道倾角约束。为了解决这些问题,本文提出了一种多约束的下沉式轨迹规划方法,规划剖面随着初始参数的变化而变化,保证了不同初始偏差下都能满足多个终端约束,提高了规划飞行末端精度。
1 飞行航迹程序设计
再入飞行器的轨迹设计问题可以看作为基准剖面的生成过程,考虑到地球旋转对再入飞行器受力影响较小,且实际飞行过程可进行制导修正。因此,轨迹规划中假设地球为均质不旋转圆球,三自由度运动方程可简化为

再入飞行器在射程能力范围内,实现终端约束任务时,即满足终端射程、高度、速度、弹道倾角任务时,需考虑合适的飞行高度剖面和速度剖面。在射程和速度约束情况,对横向规划和纵向规划进行解耦。纵向控制利用攻角和倾侧角控制速度、高度、弹道倾角以及纵向范围,横向控制利用倾侧角符号控制横向位置。
考虑再入飞行初期过程的减速问题,即用大攻角减速,倾侧角控高度,左右倾侧机动的方式进行飞行控速飞行。在飞行后期,需要考虑弹道倾角约束为正的情况下,应采用较大的正攻角策略,配合小倾侧角,拉升弹道倾角,保证终端弹道倾角约束。整个飞行航迹攻角剖面可以描述为一个类抛物线的下沉式航迹模式,其攻角剖面可描述为二次曲线形式。由于前期大攻角减速、后期小攻角拉升高度,同样,倾侧角剖面也是前期大倾侧角机动,后期小倾侧角可描述为一次曲线形式。
通过攻角、倾侧角参数化设计,对于攻角模型可描述为二次曲线形式,倾侧角模型可描述为一次曲线形式。下沉式航迹的攻角和倾侧角剖面可描述为
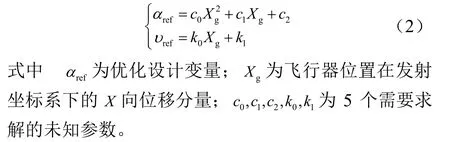
在轨迹飞行终点处,采用固定攻角、零倾侧角拉升弹道倾角,即有以下约束:

2 航迹规划问题描述
2.1 飞行航迹约束
飞行器飞行过程中,在某一参数平面内需满足各类飞行约束的飞行参数曲线。飞行过程中,复杂的飞行环境及飞行器硬件条件的限制,对再入飞行构成了一定的约束。根据飞行受到的不同影响,可分解出如下主要约束:

2.2 目标函数
飞行器轨迹规划设计的目标函数可根据任务目的及飞行器特点加以选择。考虑在给定任务参数的前提下,通常选取终端状态变量的误差值为目标函数,由于研究的飞行器目前采用到达指定速度后结束规划飞行,因此选取飞行结束后的高度和弹道倾角误差归一化后的绝对值之和最小作为目标函数,即:

2.3 优化设计变量
再入飞行器的航迹优化问题,其设计变量可取为

3 轨迹规划问题算法构建

4 仿真分析
为了验证本文提出方法的有效性,进行了再入飞行器的数值仿真计算。假设横向控制能力较高,侧滑角为零,控制变量仅为攻角和倾侧角。再入飞行器的初始速度设置为2580 m/s,初始高度为33 000 m,初始弹道倾角为0°,终端高度为29 000 m,终端速度为980 m/s,终端弹道倾角为2 °。仿真分析中飞行器模型采用洛克希德马丁公司生产的通用CAV 飞行器作为研究对象,最大升阻比为3.5,飞行器质量取1500 kg,气动参考面积1 m,气动力计算模型为
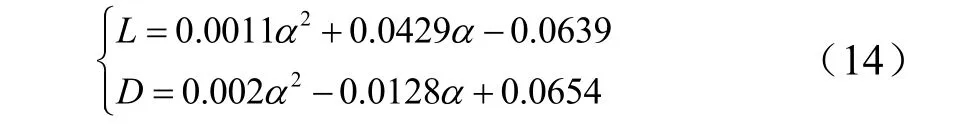
针对该飞行器模型特点,结合再入飞行的轨迹特点,其过载约束、驻点热流约束、大面积热流约束、高度约束可取值:

采用Monte-Carlo 打靶仿真考核方式,考虑质量特性偏差、气动偏差、弹体轴线偏差、大气密度偏差、风干扰偏差、初始偏差等,按照正态分布抽样取值,进行三自由度打靶概率仿真。
仿真10 000 条再入飞行轨迹,仿真结果飞行轨迹见图1 至图7。从仿真结果中可以看出速度、高度、弹道倾角都以一种二次曲线形式收敛至终端约束值,横向位置也控制在±300 m 以内,本文方法收敛有效。
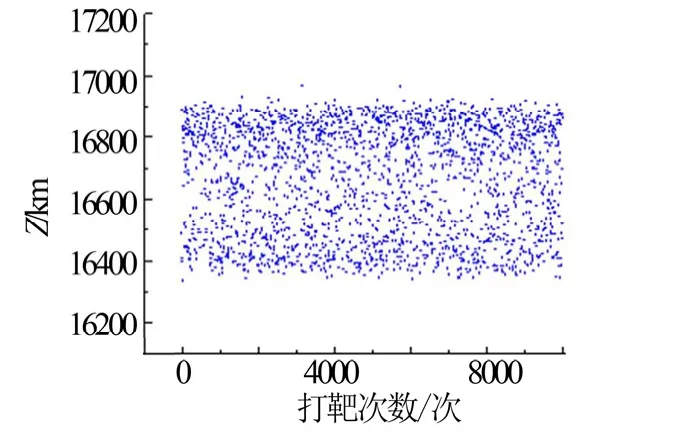
图7 飞行至目标点的终端横向位移Fig.7 Terminal Z Distribution
从图1 至图4 仿真结果可见速度收敛很快,高度和弹道倾角随着射程逐渐收敛的过程。
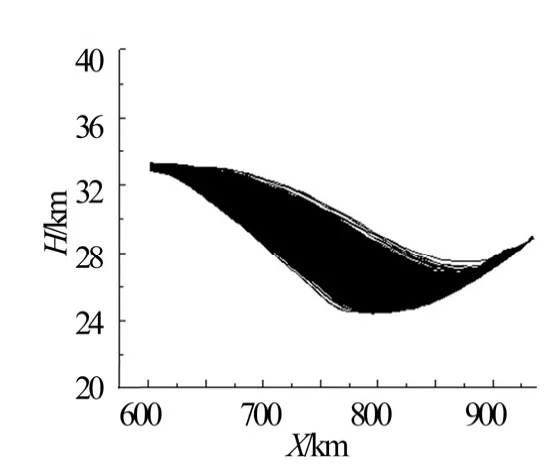
图1 射程-高度曲线Fig.1 Range and Altitude Profile
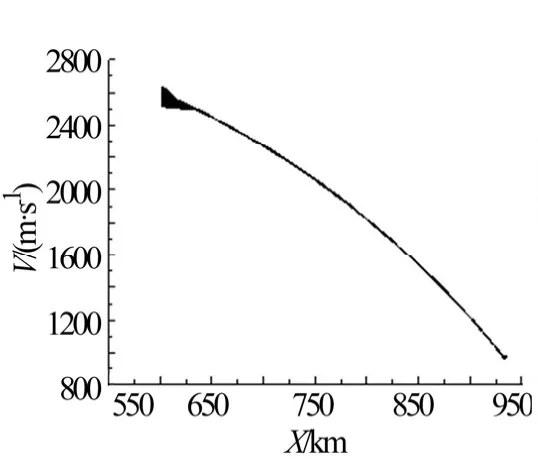
图2 射程-速度曲线Fig.2 Range and Velocity Profile
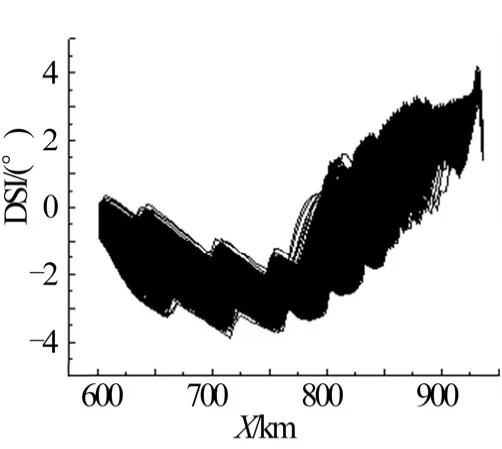
图3 射程-弹道倾角曲线Fig.3 Range and Flight Angle Profile
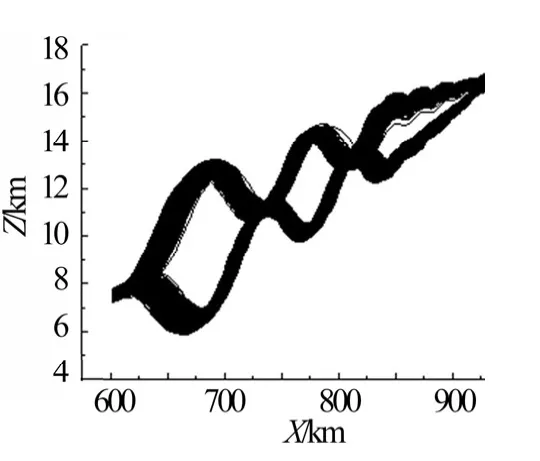
图4 射程-横向位置曲线Fig.4 Range and Z Profile
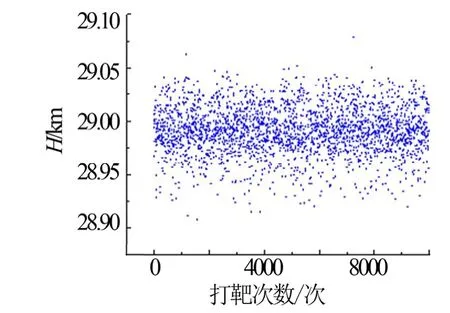
图5 飞行至目标点的终端高度Fig.5 Terminal Altitude Distribution
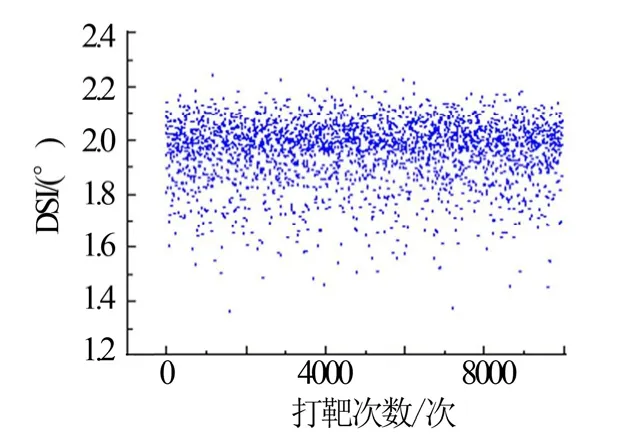
图6 飞行至目标点的终端弹道倾角Fig.6 Terminal Flight Angle Distribution
从图5 至图7 可见飞行终点处的高度、弹道倾角精度较高,终端高度控制精度均小于90 m,弹道倾角偏差小于0.7°,达到预期效果,可认为此航迹规划方法的有效性得到了验证,适合解决类似多约束条件下的弹道规划这样的复杂优化问题
5 结束语
本文的技术解决问题是:克服现有再入式飞行器航迹设计技术的不足,提出一种再入飞行器下沉式轨迹规划设计方法,可适应能力范围内的射程、高度、速度、弹道倾角等多种约束,利用粒子群优化算法解算飞行轨迹规划问题,解决传统平衡飞行航迹存在弹道倾角不可控、计算量大、寻优效率低的问题。
a)本文针对再入飞行器质点运动控制机理,提出了一种针对再入飞行器在射程能力范围的航迹剖面规划技术,解决了再入飞行器传统轨迹规划方法中缺少考虑弹道倾角、弹道偏角约束的问题,确保了多约束飞行任务的可实现性。
b)针对飞行器多约束问题,提出一种多约束条件下精确控制技术,解决了满足终端射程、高度、速度、弹道倾角、弹道偏角和过程约束轴向过载、法向过载和动压的精确控制难题,适用于终端约束多、过程约束复杂、精度指标高的飞行任务,具有极高的通用性。
c)针对飞行轨迹规划求解问题,提出了一种改进粒子群优化算法求解方法,解决了航迹规划程序角剖面求解时的设置参数少、收敛速度快、可适用于复杂非线性规划问题,易于工程实现,具有更广的适应性等优点,是一种更加高效的轨迹规划问题求解方法。

