基于热响应特性的高速飞行器多约束轨迹优化
许 昱,贺峥光,薛鹏飞,李振华,余卓阳
(1. 空间物理重点实验室,北京,100076;2. 中国运载火箭技术研究院,北京,100076)
0 引 言
高速飞行器具备飞行速度快、机动能力强、投送距离远等优势,已成为航空航天领域的战略制高点。随着对飞行速度的要求不断提高,高速飞行器所面临的热防护问题愈加复杂和严峻,加强各专业耦合度并开展多学科优化设计是解决该问题的方式之一。
在传统的轨迹设计过程中,为防止高速飞行器的结构因气动热作用而产生破坏,采用限制驻点热流和总加热量的热约束方式进行热控制。但从气动加热的相关研究中可见,造成高速飞行器结构热破坏的直接因素是温度超过极限,而非热流超过极限,限制驻点热流和总加热量存在约束表征不合理的缺陷。此外,传统的热约束方式还存在以下不足:
a)对于采用防热承力一体化的高速飞行器而言,难以在机体上安装低温热沉作为冷端,因此无法使用热流传感器获取相应的热流和总加热量;
b)以CAV 为代表的高速飞行器具有尖锐的端头,设计时通常在端头处留有部分柱段允许其烧蚀,而将热防护的研究重点放在大面积机体上,因此过度限制驻点热流会影响高速飞行器的机动能力;
c)工程实际中采用包络设计方法,将轨迹设计和热防护分析交替进行,导致设计过程存在反复迭代、相互妥协的现象,难以获得最优的轨迹。
综上所述,采用传统热约束的轨迹设计方法存在约束表征不合理、难以实际测量、容易过约束、影响研制效率等缺陷,因此需要建立能够动态表征热响应过程的高速飞行器动力学模型,通过限制大面积机体内外壁面温度上限的方式进行热约束。
本文基于一维多层平板传热理论建立高速飞行器传热与热响应模型,并以传统飞行力学为基础,通过热环境近似拟合和热响应方程形式变换,建立包含有热响应模型的高速飞行器增广动力学模型。在对增广动力学模型热响应特性开展深入研究的基础上,使用自适应Radau 伪谱法对以内壁温度最低为优化目标的高速飞行器多约束轨迹优化问题进行求解,并对优化设计结果的合理性和科学性进行分析。
1 高速飞行器增广动力学模型的建立
1.1 热响应模型建立与变换
被动热防护系统具有简单可靠、技术成熟度高、应用范围广等优势,本文将其作为建立热响应模型的研究对象。被动热防护系统通常采用防热层+隔热层的设计方案,同时一维传热模型即可满足初步分析的精度要求。故基于一维多层平板传热理论建立传热与热响应模型,如图1 所示。
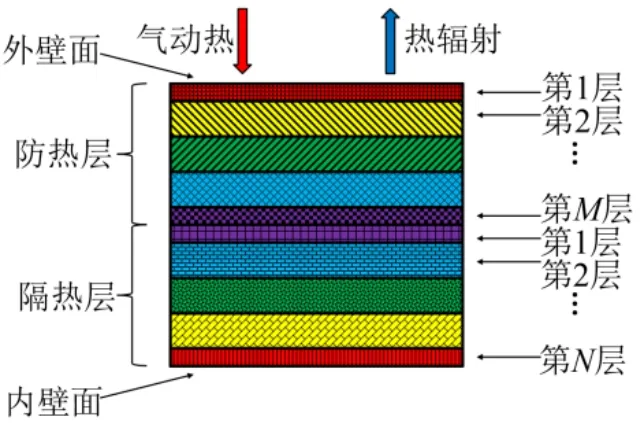
图1 一维多层平板传热模型Fig.1 One-dimensional Multi-layer Plates Heat Transfer Model
该模型由一系列连续的、不同材料、不同厚度的平板组成,存在沿厚度方向的连续传热。其控制方程可表示为
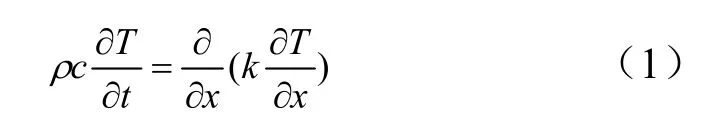
式中,,,分别为防隔热层材料的密度、比热容、导热系数和温度。
外壁面能量平衡方程为
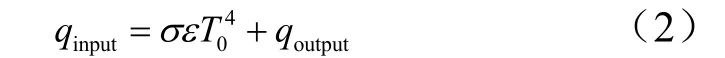

首先对一维多层平板结构进行空间离散,得到由多个控制单元组成的区域。其中,各控制单元厚度需权衡材料的物性参数和计算规模综合选取。然后采用控制容积积分法对控制方程进行离散处理,可得:
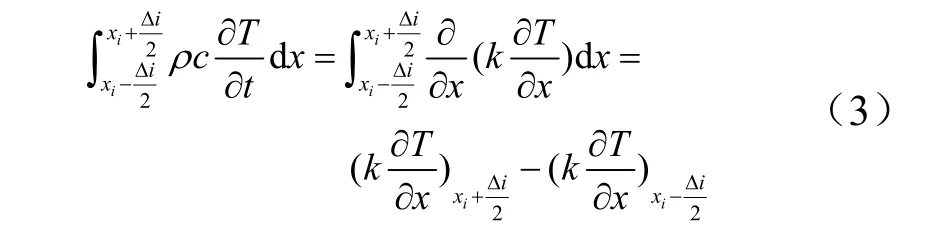
最终得到的一维多层平板传热与热响应模型为
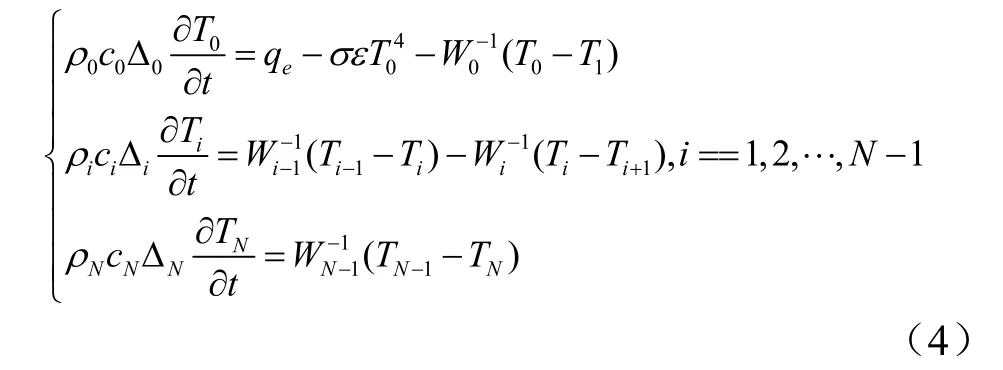
1.2 高速飞行器动力学模型
为突出研究重点,采用如下假设:
a)地球为均质圆球,不考虑其自转和公转;
b)高速飞行器全程无动力飞行,质量不变;
c)高速飞行器满足瞬时平衡,侧滑角为零;
d)仅考虑飞行器的纵向运动,倾侧角为零。
由此可得高速飞行器简化的质心动力学模型为
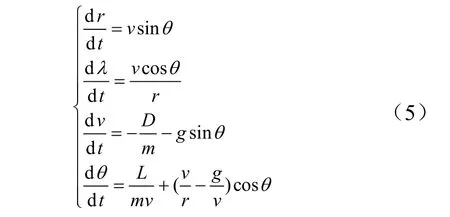
式中为地心距;为航程角;为飞行速度;为轨迹倾角;和分别为飞行器的升力和阻力;为飞行器质量;为重力加速度。
1.3 高速飞行器增广动力学模型
将式(5)和(4)联立,得到包含热响应模型的高速飞行器增广动力学模型:
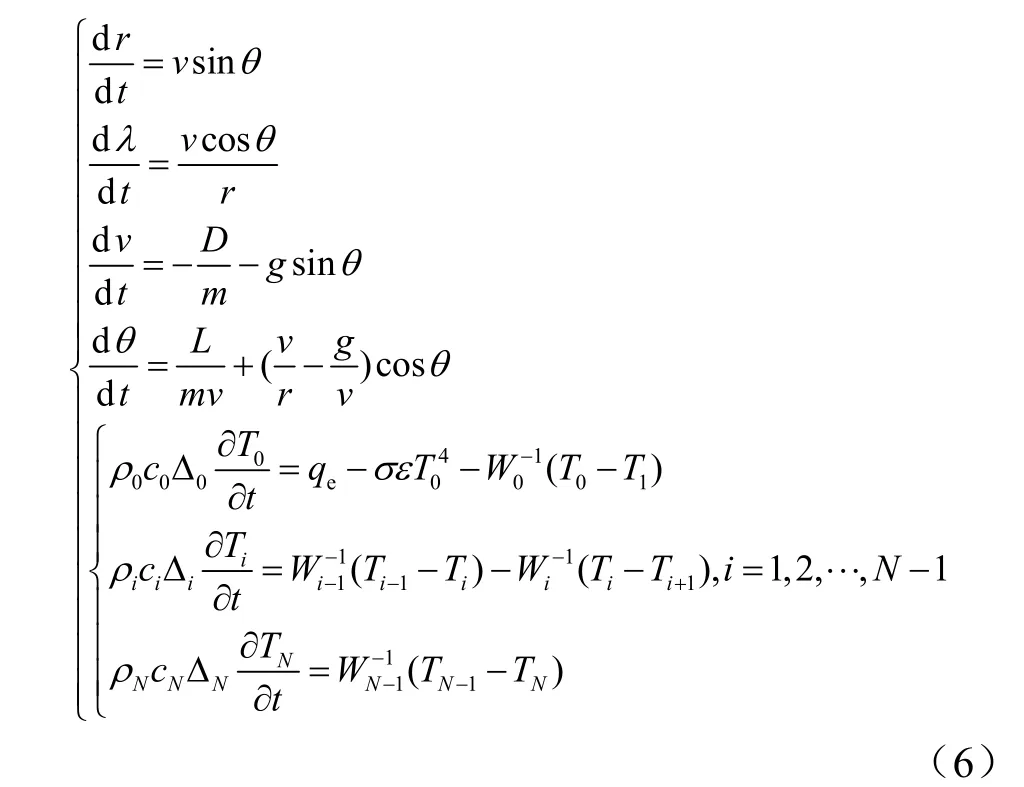
可见,动力学模型与热响应模型通过热流建立联系,模型之间的相互影响较小,因此可在消耗少量计算资源的前提下实现对微分方程组的求解。
2 高速飞行器增广动力学模型的分析
2.1 仿真环境设定与防隔热层物性参数
以通用航空飞行器CAV-H 为研究对象,其质量为907 kg,参考面积为0.4839 m,升力和阻力系数参考文献[11]进行拟合。
通过将全飞行剖面内的状态进行网格离散,使用近似拟合方法得到高速飞行器表面(迎风面1 m 处)的气动热流可表示为

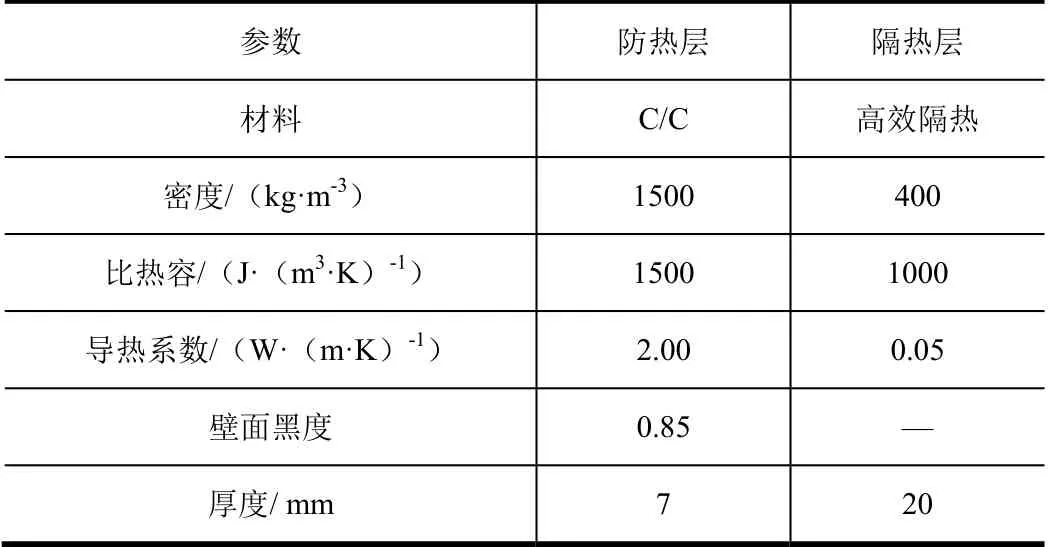
表1 防隔热层物性参数Tab.1 Physical Parameters of Thermal Protection Layer and Thermal Insulation Layer
通过仿真与分析,选取防隔热层的离散层数分别为2 和8,从而满足所需的求解精度和计算效率。
2.2 不同飞行模式对热响应特性的影响
仿真初值和终止条件设定如表2 所示。

表2 动力学模型热响应特性测试的条件设定(1)Tab.2 Setting for Thermal Response Characteristic Test for Flight Dynamic Model (1)
约束条件设定为:过载不超过15;动压不超过500 kPa;迎风面1 m 处的外壁温度不超过1273 K,内壁温度不超过573 K。仿真结果如图2、图3 所示。
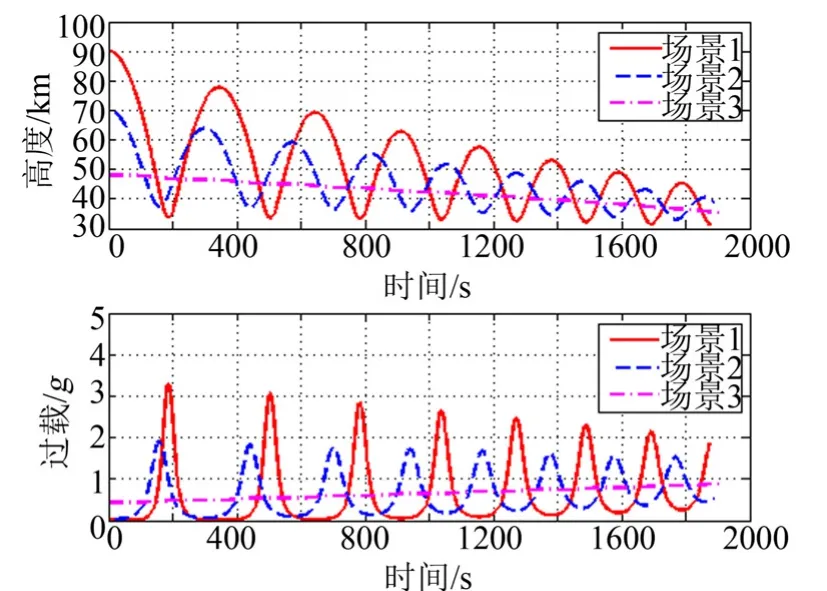
图2 高度/过载-时间变化Fig.2 The Variation of Height/Overload with Time
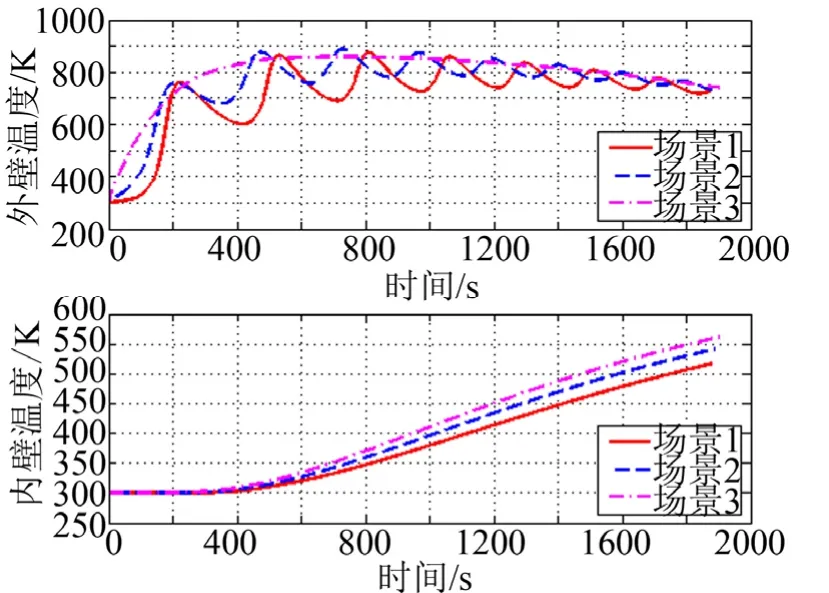
图3 外壁/内壁温度-时间变化Fig.3 The Variation of Outer/Inner Wall Temperature with Time
由图2、图3 可见,初始高度不同时,高速飞行器的飞行模式存在较大差异,场景3 采用平衡模式,而场景1 和2 采用跳跃模式。平衡模式的特点在于轨迹较为平直,过载和动压的峰值低、变化小,内壁温度较高;跳跃模式则相反,其轨迹波动较为剧烈,过载、动压和外壁温度均出现大范围跳动,但内壁温度相对较低。由结果可知,在满足多约束的前提下,场景1的内壁温度相较场景3 可降低44.8 K。
2.3 不同飞行攻角对热响应特性的影响
仿真初值和终止条件设定如表3 所示。

表3 动力学模型热响应特性测试的条件设定(2)Tab.3 Setting for Thermal Response Characteristic Test for Flight Dynamic Model (2)
约束条件设定同上,仿真结果如图4、图5 所示。
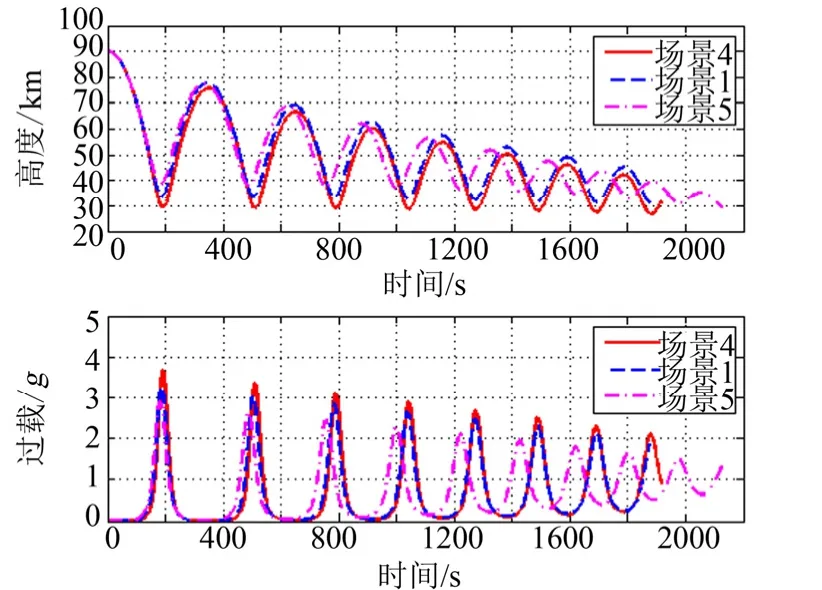
图4 高度/过载-时间变化Fig.4 The Variation of Height/Overload with Time
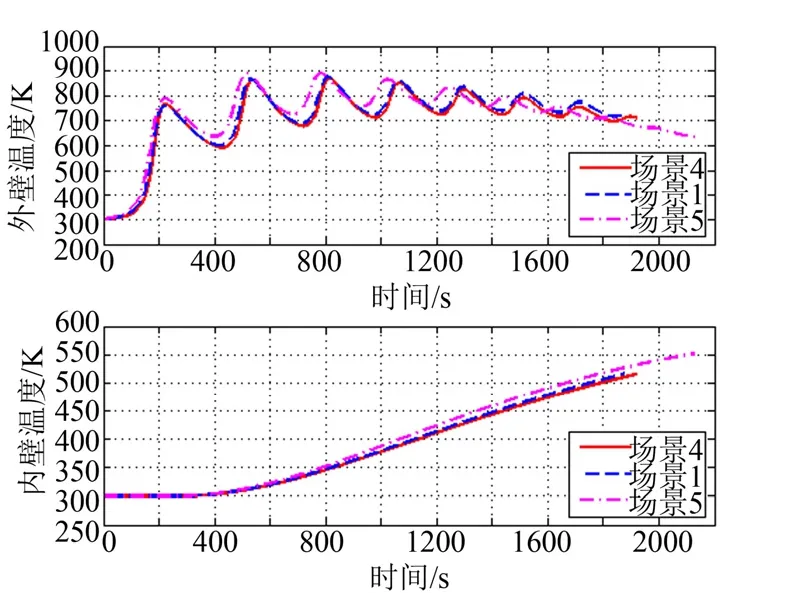
图5 外壁/内壁温度-时间变化Fig.5 The Variation of Outer/Inner Wall Temperature with Time
由图4、图5 可见,采用小攻角的起跳高度较低,导致过载和动压的峰值较大、波动较为显著,但内壁温度得到较好的控制。由结果可知,在满足多约束的前提下,场景4 的内壁温度相较场景5 可降低36.7 K。
3 基于热响应特性的多约束轨迹优化
3.1 轨迹优化问题概述
轨迹优化问题通常表现为非线性、带有状态约束和控制约束的最优控制问题,通过寻找既可满足各类约束又能使性能指标最优的控制规律,从而得到问题的最优解,并给出状态量的变化情况。伪谱法是数值求解最优控制问题的一种方法,采用全局插值多项式在一系列离散点上近似状态量和控制量,并通过伪谱差分矩阵将微分方程约束转化为代数方程约束,从而将最优控制问题转化为非线性规划问题,再使用数值方法求解非线性规划问题即可获得最优轨迹。

自适应Radau 伪谱法结合h 方法和p 方法的优点,根据预先设定的判据自主决定采用网格区间重新划分还是增加多项式阶数的方法来达到精度要求,从而完成非线性规划问题的求解,相较于传统Radau 伪谱法可具备更高的求解精度和计算效率。
3.2 以内壁温度最低为优化目标的多约束轨迹优化
本文采用自适应Radau 伪谱法进行最优控制问题的转换,使用SNOPT 求解非线性规划问题,从而得到以内壁温度最低为优化目标的多约束轨迹优化结果。优化设计的条件设定如表4 所示。
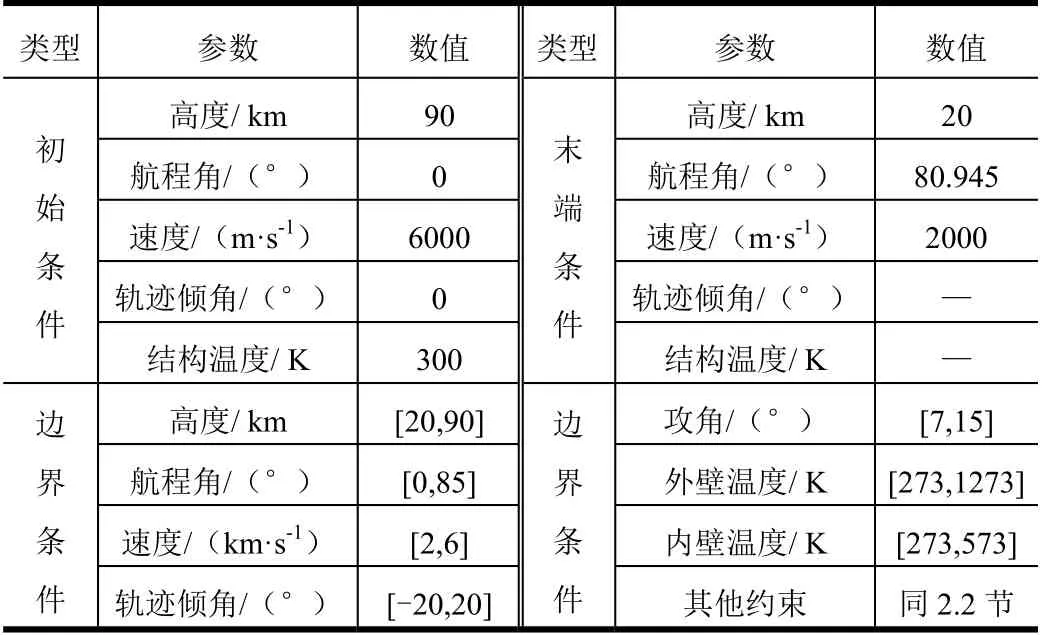
表4 多约束轨迹优化的条件设定Tab.4 Setting for Multiple Constraints Trajectory Optimization
优化结果如图6、图7 所示。
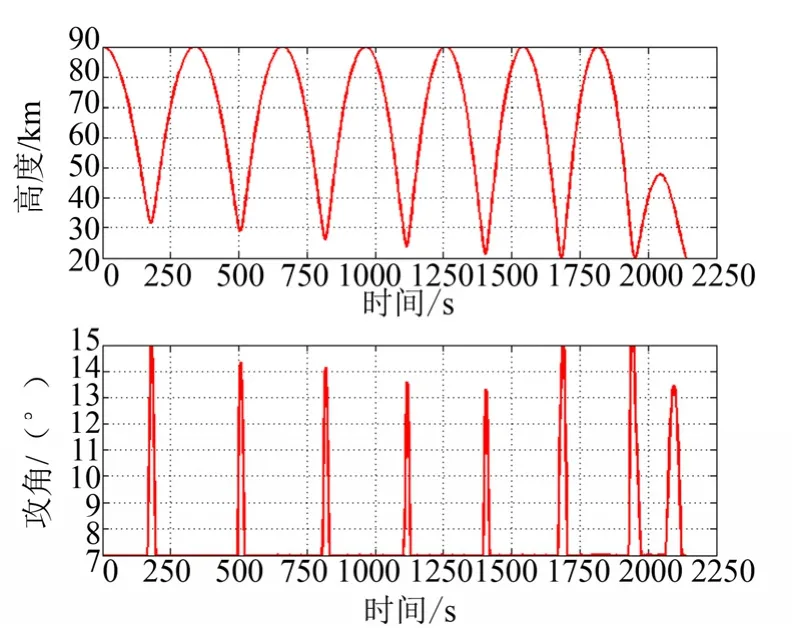
图6 高度/攻角-时间变化Fig.6 The Variation of Height/AOA with Time
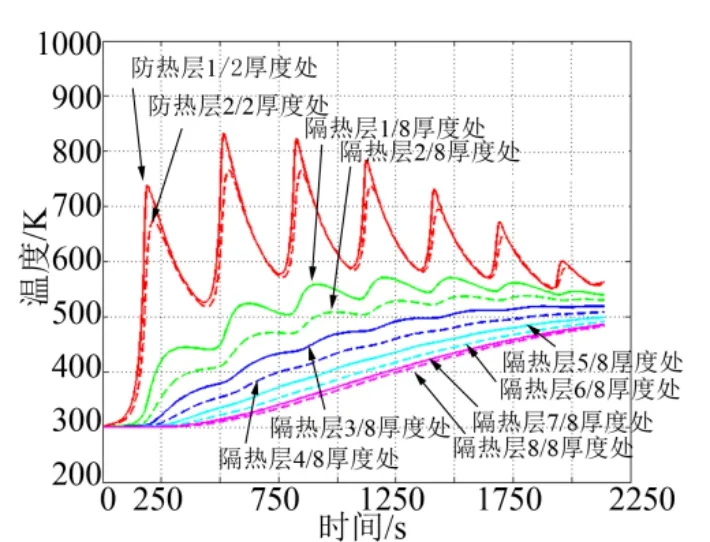
图7 温度-时间变化Fig.7 The Variation of Temperature with Time
由图6、图7 可见,高速飞行器采用跳跃飞行模式,具体表现为在大气密度较低的中间层(50~90 km)采用小攻角使飞行器表面热流较小(详见式(7)),然后在大气密度可满足起跳条件的平流层(11~50 km)采用大攻角将飞行器迅速拉起抬升,以避免较大气动热流的长时间加热作用。该优化轨迹相较定攻角、平衡飞行模式(场景3)可降低内壁温度78.4 K,相较定攻角、跳跃飞行模式(场景1)可降低内壁温度33.6 K,优化效果明显,实现预期目标。
4 结 论
本文针对高速飞行器传统轨迹设计方法所存在的热约束表征不合理和过约束的问题,以一维多层平板传热理论为基础,通过热环境近似拟合和热响应方程形式变换,建立包含热响应模型的增广高速飞行器动力学模型。从而在轨迹设计时能够充分考虑到飞行器结构的温度变化过程,并根据其热响应特性设计出使内壁温度更低的飞行轨迹。所得到的结论如下:
a)在满足各类约束的前提下,采用跳跃飞行模式能够显著降低飞行器的内壁温度,该飞行模式可作为轨迹设计层面进行内壁温度控制的方法;
b)使用自适应Radau 伪谱法开展多约束轨迹优化问题的求解,得到的优化轨迹相较于采用最佳升阻比攻角跳跃飞行能够进一步降低内壁温度。

