基于一致性算法的微电网谐波功率均分控制方法

江世明，唐 杰

（1.湘西南农村信息化服务湖南省重点实验室，邵阳 422000；2.邵阳学院信息工程学院，邵阳 422000）

随着全球生态环境污染加剧，具有清洁无污染、安装地点灵活等优点的分布式发电DG（distrib⁃uted generation）受到日益显著的关注，并逐渐成为未来电网的有力支撑[1-4]。微电网作为分布式发电单元接入电网的纽带，将多种清洁能源、储能装置、电力电子变换装置有机整合，对提高新能源的消纳能力有着重要意义，具有十分广阔的发展前景[5-6]。

在孤岛微电网中，由于DG和负载随机接入微电网的节点，导致微电网结构变得更加复杂，因此精确的功率均分也更加难以实现。微电网孤岛运行时，大量非线性负载接入微电网带来大量的谐波电流，引起微电网电压畸变[7]，此外，线路阻抗差异会导致谐波电流在各逆变器之间不能均匀分配，从而可能造成某些DG过载。因此，微电网孤岛运行时，各并联逆变单元如何按照容量均分负载谐波电流并改善微电网的电压质量是微电网稳定运行的一个重要问题。

针对谐波均分的问题，现有文献提出了许多控制策略。文献[8]通过引入较大的虚拟阻抗，弱化线路阻抗差异影响，提高谐波均分精度，然而过大的谐波虚拟阻抗会严重恶化微电网的电能质量；为了改善微电网电压质量，文献[9]提出了基于虚拟阻抗的谐波抑制策略，通过引入谐波电流前馈构造呈容性的谐波虚拟阻抗，结合准比例谐振控制减小谐波阻抗，从而提高输出电压的电压质量，但是未考虑谐波电流均分问题；文献[10]提出一种基于虚拟阻抗的下垂控制策略，所提方法直接控制PCC电压，并通过引入虚拟阻抗，实现功率分配和谐波电流均分；文献[11]考虑逆变器以不同模式即电压控制模式VCM（voltage control mode）和电流控制模式CCM（current control mode）运行，提出了一种具有高谐波电流均分精度的适用于VCM和CCM的电压谐波抑制策略，所提控制策略通过多带通滤波器提取PCC点谐波电压分量重构谐波阻抗；文献[12-13]通过采样PCC处的线路电流和电压，在谐波频率下调节虚拟阻抗，以补偿馈线和线路阻抗的不匹配，从而改善系统非线性负载的功率分配性能。然而文献[10-13]所提方法都需要采样PCC电压，而实际应用中，由于PCC和微控制器之间的距离比较远，因此可能会导致采样的PCC电压信号存在衰减和延时，进而影响谐波抑制和电流均分的效果。

文献[14-15]提出了一种基于集中式控制的谐波电流均分控制方法。其中，文献[14]通过引入谐波虚拟阻抗，并通过集中式控制方法动态调整谐波虚拟阻抗的幅值，解决谐波电流均分的问题；文献[15]提出了一种在线虚拟阻抗调整的下垂控制方法，将与DG谐波功率相关的物理量添加到有功频率下垂控制中，通过检测该物理量的变化构造谐波虚拟阻抗。然而文献[14-15]中所提方法都需要中央控制器，导致系统的可靠性和灵活性低，对通讯依赖性强，单点通信故障会严重影响系统谐波功率均分性能。

为了克服集中式控制的缺点，提高系统的可靠性和可扩展性，文献[16-17]提出了一种基于分布式控制的谐波电流均分方法。其中，文献[16]通过基于一致性算法的分布式控制方法构造谐波虚拟阻抗，以匹配线路阻抗，实现谐波功率均分，然而也尚不清楚所提控制方法是否能应用于具有复杂拓扑结构的微电网；文献[17]通过引入输出电流前馈构造呈阻性的谐波虚拟阻抗，并通过基于一致性算法的分布式控制动态调节虚拟阻抗的值，提高功率均分精度，然而所提方法需要在谐波功率均分精度和电压质量之间进行折衷。文献[18-19]采用基于一致性算法的分布式控制，然而并未讨论谐波均分和电压质量改善问题。

现有研究通常是通过引入谐波虚拟阻抗解决谐波均分问题，然而虚拟阻抗的引入会导致需要在谐波均分精度和电压质量之间折衷的问题。此外，尚不清楚现有控制方法是否能适用于具有复杂拓扑结构的微电网。针对此，本文提出基于一致性算法的阻抗重构控制方法，通过引入输出电压谐波分量反馈和阻抗重构因子自适应控制，自适应重构逆变器谐波阻抗，提高谐波均分精度和电压质量。所提控制方法无需检测线路阻抗和微电网结构，能适用于结构变化的、含复杂拓扑结构的微电网。通过仿真和实验都验证了所提控制策略的正确性和有效性。

1 独立微电网运行机理

图1为多逆变器并联的孤岛微电网示意。由于分布式发电单元DG和负载接入的位置随机，因此微电网转变为具有复杂拓扑形式的微电网，如图1所示。图中，Lline和Rline表示线路阻抗的感性部分和阻性部分，Lnet和Rnet表示馈线网络中馈线阻抗的感性部分和阻性部分，L.l表示DG侧的本地负载（local load），P.l表示连接在系统其他节点的公共负载（public load）。主要考虑谐波均分和电压质量提升的问题，本文负载主要是以非线性负载为主。图1中虚线表示分布式通信网络，只有相邻DG之间才进行通信。

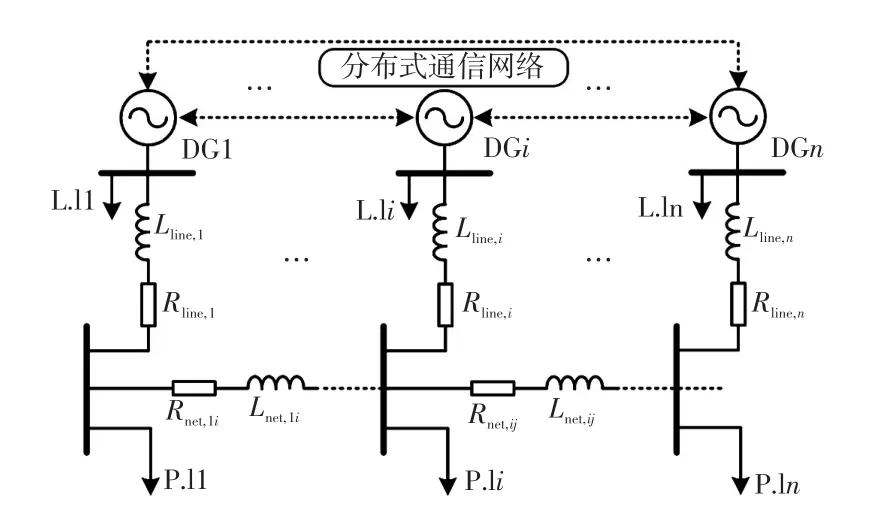
图1 含分布式通信网络的微电网结构Fig.1 Structure of microgrid with distributed communication network

2 谐波均分特性分析

在具有高比例非线性负载的微电网中，谐波电流的不准确共享会导致分布式电源过载。此外，谐波会导致过热、损耗增加、电流和电压波形失真等。以2个DG分析谐波均分特性，图2所示为谐波域下2台DG的简化电路。

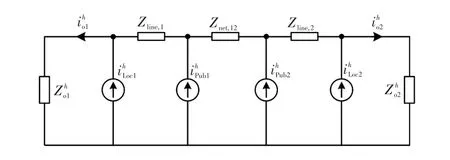
图2 在谐波频率处2台DG的等效电路Fig.2 Equivalent circuit of two DGs at harmonic frequencies

通常解决谐波均分的方案是通过引入谐波虚拟阻抗的方法重塑逆变器输出阻抗。由于非线性负载的不均匀分配主要是由于线路阻抗差异导致的，为了保证谐波功率均分精度，在重塑逆变器等效谐波阻抗时，通常设计较大的谐波虚拟阻抗，以便弱化线路阻抗差异，当谐波虚拟阻抗与线路阻抗相比占主导地位时，可以实现谐波功率均分。然而，较大的谐波虚拟阻抗会恶化电压质量。因此需要在谐波功率分配精度和电能质量之间进行的权衡。

3 自适应虚拟阻抗重构控制策略

本文所提控制方法不需要引入复杂的谐波虚拟阻抗控制，通过引入逆变器输出电压谐波分量反馈，重构逆变器等效谐波阻抗。所提控制方法通过减小谐波阻抗可以实现两个目标：一是通过减小谐波阻抗可以提高微电网的电压质量；二是可以减小谐波功率均分误差，实现谐波的精确均分。所提控制方法不需要检测线路阻抗，也不受微电网拓扑结构的影响，采用基于一致性算法的分布式控制方法，能够提高系统的灵活性和可拓展性。相比传统的引入谐波虚拟阻抗的方法，所提方法在实现谐波精确分配的同时，能够提高微电网的电压质量。

3.1 基于图论的一致性控制算法

3.2 基于一致性算法的自适应阻抗重构控制

图3 所提控制方法的控制框图Fig.3 Control block diagram of the proposed control method

图3中虚线方框的原理可以通过如图4所示的含谐波电压前馈的控制框图表达。

图4 含谐波电压前馈的控制框图Fig.4 Control block diagram with harmonic voltage feedforward

综合上述分析，施加本文所提控制方法后，逆变器谐波阻抗幅值如图5所示。

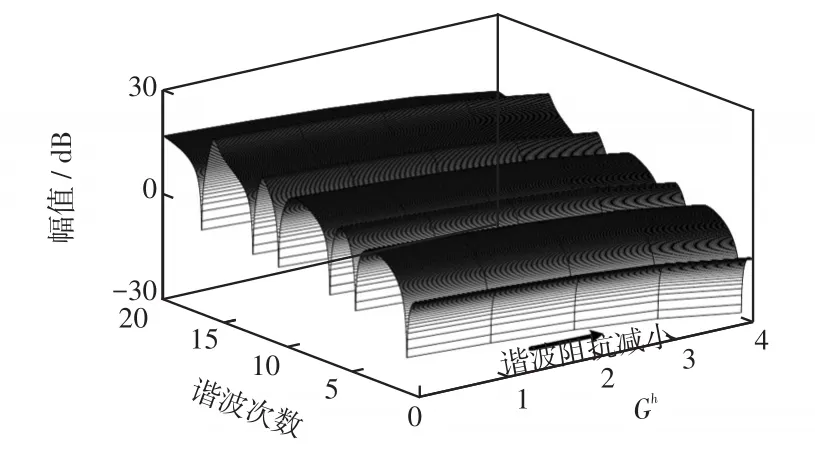
图5 谐波阻抗Fig.5 Harmonic impedance

从图5中可以看出，随着Gh的增大，逆变器的谐波阻抗会减小。因此对多逆变器并联的系统而言，从PCC处看的总等效谐波阻抗也会减小，所以微电网的电压质量会得到提高。

4 稳定性分析

图6所示为kq从1增加到50时系统特征值的轨迹。从图6可见，随着kq的变化，λ1和λ2一直位于s平面的负半平面，并且远离虚轴向左移动，系统的快速性能得到一定程度的提高，而主要影响稳定性的是λ3、λ4和λ5；随着kq的增加，主导极点λ3在负实轴上从左往右靠近虚轴，主导极点λ4和λ5从负半平面向着虚轴移动；从特征值λ4和λ5的变化趋势中看出，随着kq的增加，系统的阻尼将变小。当kq约等于47，λ3，λ4和λ5进入右半平面，系统变得不稳定。事实上，过大的kq表示会引入过大的谐波电压前馈，从而可能会导致系统的不稳定。此外，在实验中，由于电压采样会存在采样误差等问题，而过大的kq将会放大这个采样误差，因此也可能会导致系统的不稳定。而系统的稳定性是最重要的，均分的快速性往往不是最首要考虑的，因此综合上述分析，本文选取kq=20。

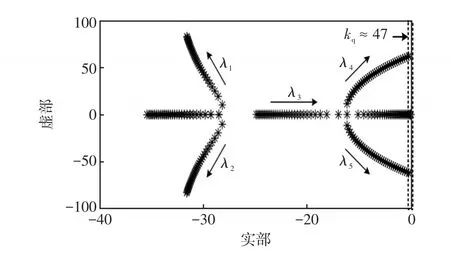
图6 kq变化时特征值的根轨迹Fig.6 Loci of eigenvalues with variation inkq

5 仿真与实验验证

为了验证本文所提控制策略的有效性，在Mat⁃lab/Simulink中搭建5台DG并联的仿真模型，仿真所用电路结构如图7所示，其中负载包括三相不可控整流电路、阻感性线性负载。主电路的参数以及控制部分的详细仿真参数如表1所示。

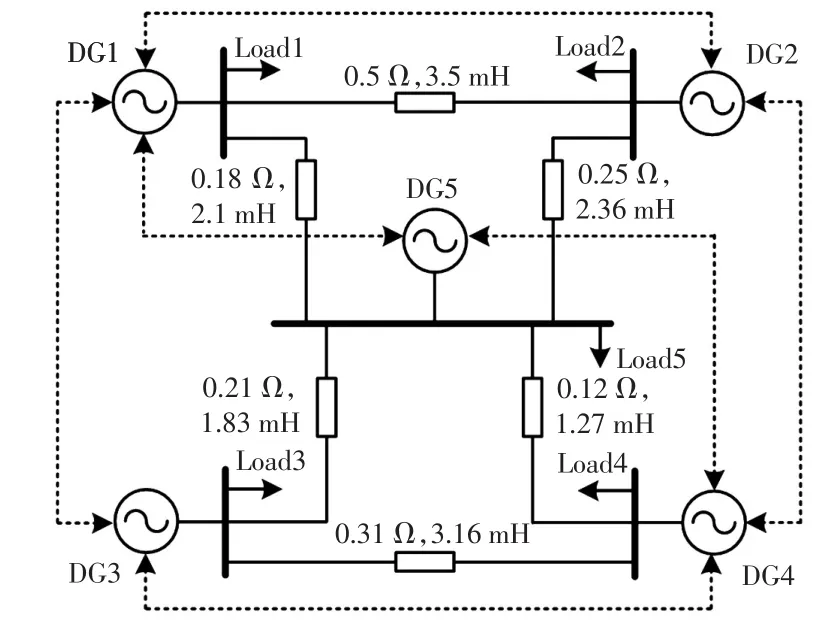
图7 用于仿真验证的电路结构Fig.7 Circuit structure for simulation verification

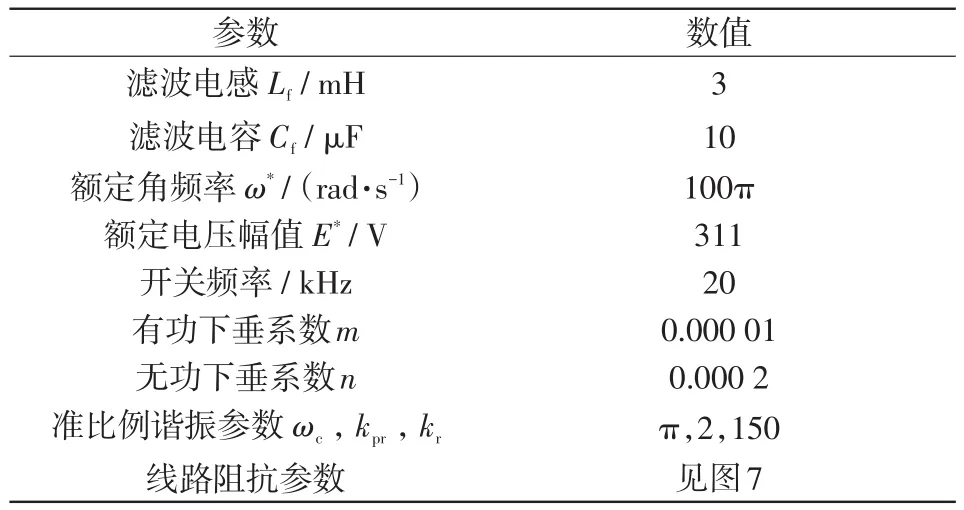
表1 系统仿真参数Tab.1 Simulation parameters of system

5.1 DG容量相同情况

仿真中，0.4 s时施加所提阻抗重构控制，1.1 s时通信中断，DG5和DG4之间的通信链路断开，1.4 s时负载突增。

图8为5次谐波功率和7次谐波功率仿真波形。从图中可见，0.4 s前，各台DG的谐波功率互不相等，对应的5次谐波电流波形如图9（a）所示，谐波电流也互不相等。0.4～1.1 s，各台DG谐波功率相等，此时对应的5次谐波电流波形如图9（b）所示，由图可见此时各台DG的5次谐波电流相等。1.1～1.4 s时，从图8可见，通信中断对谐波均分没有影响，系统依然保持着很好的谐波均分精度。可以这样理解，在通信中断时，系统已经达到了稳态，此时各台DG的阻抗重构因子由于积分的“记忆”作用保持不变，因此即使发生通信中断，也不会影响谐波均分效果。1.4 s时，负载增加，从图9（c）可见，各台DG的5次谐波电流依然相等。7次谐波电流情况和5次谐波电流情况一样，此处不再赘述。

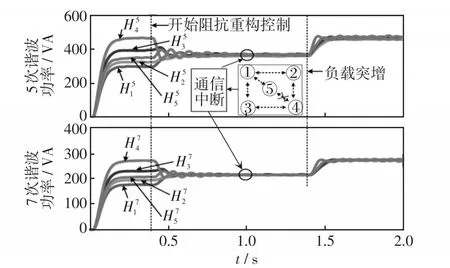
图8 相同容量DG时谐波功率仿真波形Fig.8 Simulation waveforms of harmonic power when DGs have the same power ratings

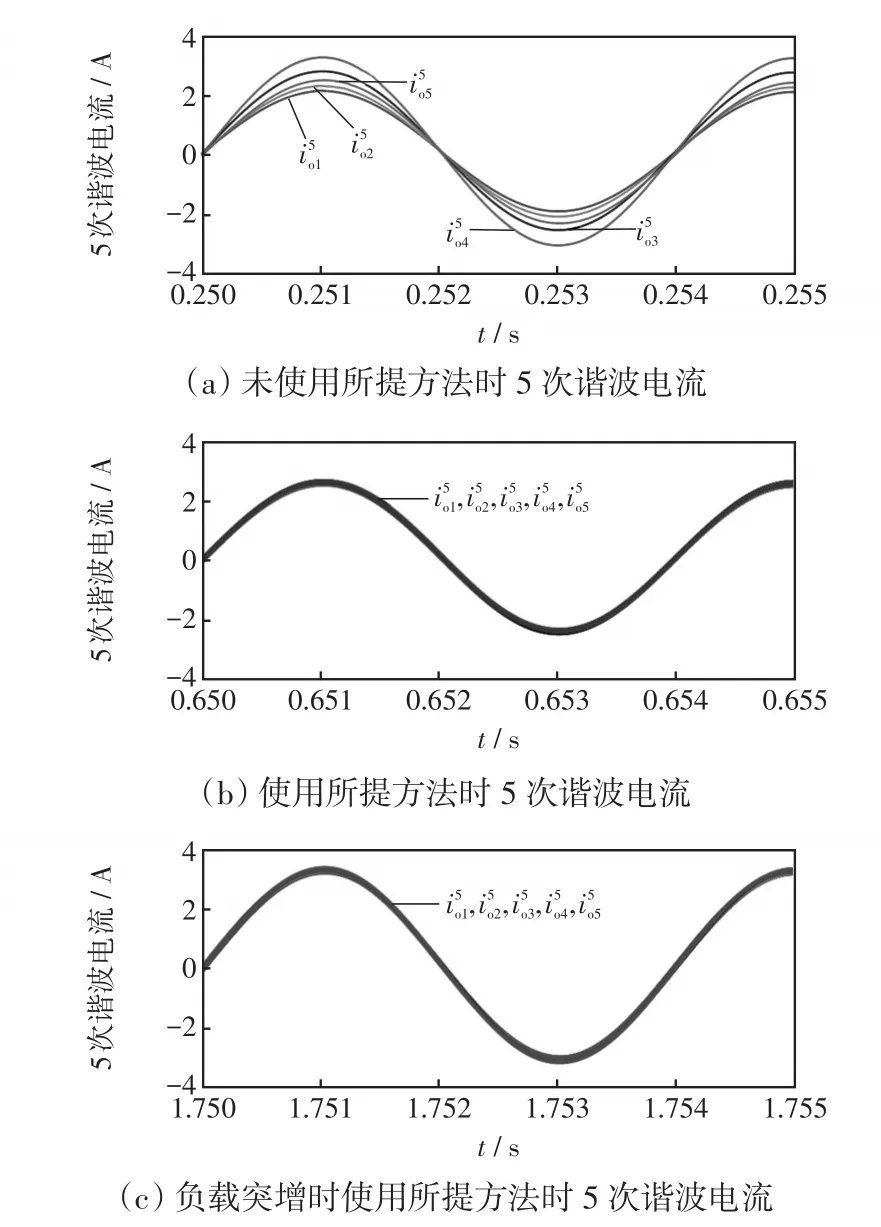
图9 相同容量DG时施加所提控制方法前后谐波电流仿真波形Fig.9 Simulation waveforms of harmonic currents when DGs have the same power ratings before and after using the proposed method

图10为施加所提控制方法前后的电压波形和电压畸变率。图10（a）为未施加所提控制方法时的仿真结果，此时5次和7次谐波含量高，电压波形质量较差，THD达到了6.24%。施加所提控制方法时的电压波形和THD如图10（b）所示，此时5、7和11次谐波含量明显降低，电压波形质量得到较大改善，THD降低为2.35%，满足了低于5%的要求。

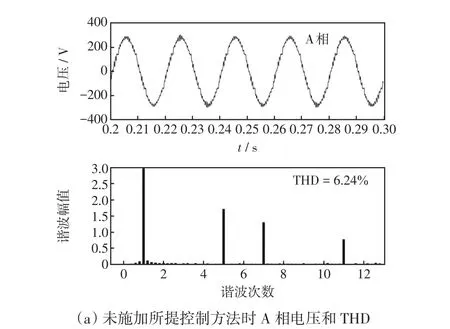
图10 A相电压波形和THD对比Fig.10 Comparison of phase A voltage waveforms and THD

5.2 DG容量不同情况

DG容量不同且容量比满足1∶2∶2∶3∶4时，仿真中0.4 s施加所提控制方法。从图11中可知，未施加所提控制方法时，容量最大的DG5的谐波功率并不是最大的，反而容量不是最大的DG4的谐波功率最大，此时5次谐波电流波形如图12（a）所示，DG4的谐波电流最大，容易造成DG4过载。0.4 s时开始阻抗重构控制，达到稳态时，各台DG的谐波功率比约为1∶2∶2∶3∶4，表明实现了谐波功率按容量分配，此时5次谐波电流图如图12（b）所示，可知谐波电流比也为1∶2∶2∶3∶4。1.4 s时，负载突增，如图11和图12（c）所示，各台DG的谐波功率和谐波电流均有所增加，并且依然都满足1∶2∶2∶3∶4的比例关系。7次谐波电流情况和5次谐波电流情况一样，在此不在赘述。

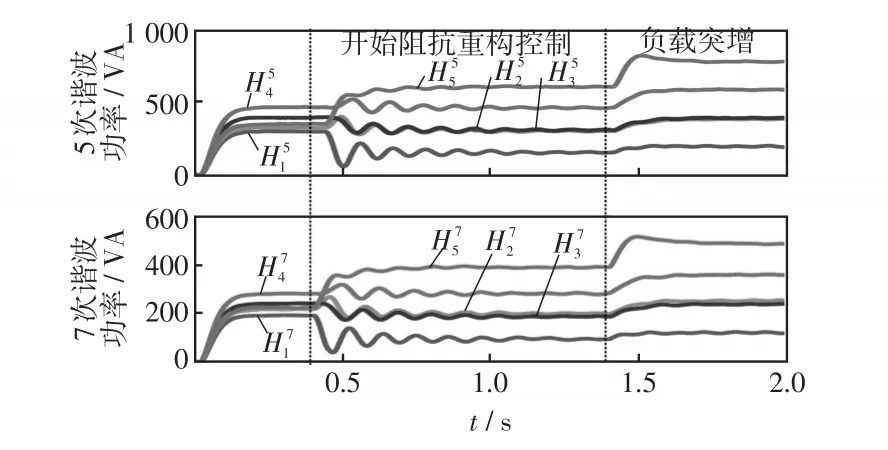
图11 不同容量DG时谐波功率仿真波形Fig.11 Simulation waveforms of harmonic power when DGs have different power ratings

图12 不同容量DG时施加所提控制方法前后谐波电流仿真波形Fig.12 Simulation waveforms of harmonic currents when DGs have different power ratings before and after using the proposed method

5.3 线路中断和DG退出运行情况

本部分验证所提控制方法在线路中断和DG退出运行情况下的有效性。根据图7所示，在仿真中1.0 s时DG1和DG5的线路中断，1.5 s时DG2退出运行，图13为各台DG的谐波功率波形，图14为施加所提方法前后谐波电流仿真波形。线路中断后，系统经过短暂的变化过程达到稳态后，各台DG的谐波功率依然相等，对应的电流波形如图14（c）所示。1.5 s时，DG2退出运行，经过短暂的变化过程后，DG2的谐波功率降为0，谐波电流也变为0，而在运行中的其他DG的谐波功率增加，并且依然相等，此时的谐波电流波形如图14（d）所示。负载突增、线路中断和DG退出运行，均会改变微电网的拓扑结构，即便如此，所提控制方法依然能实现谐波的精确分配。

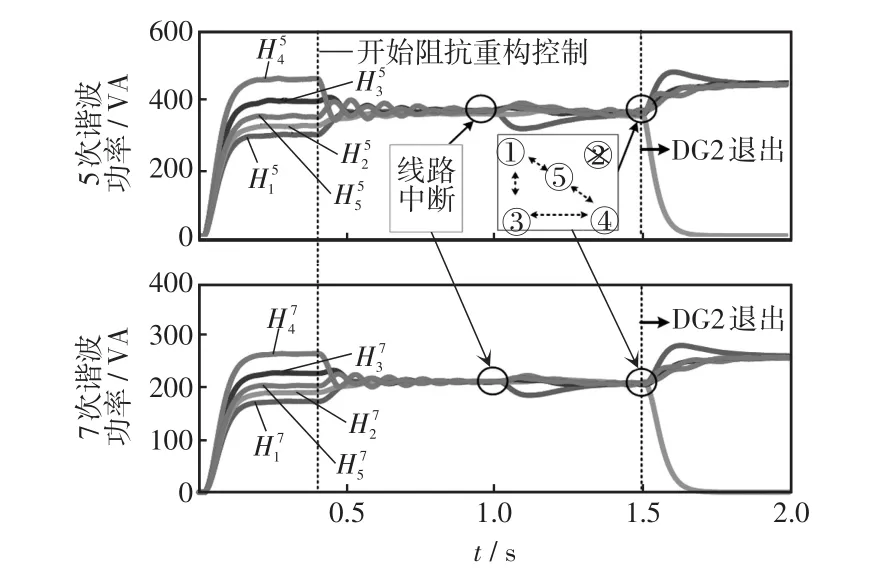
图13 线路中断和DG退出时的谐波功率仿真波形Fig.13 Simulation waveforms of harmonic power when line is interrupted and DG plugs out

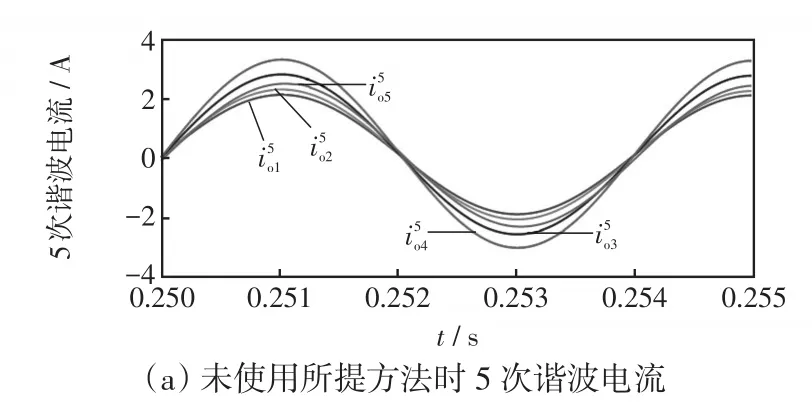
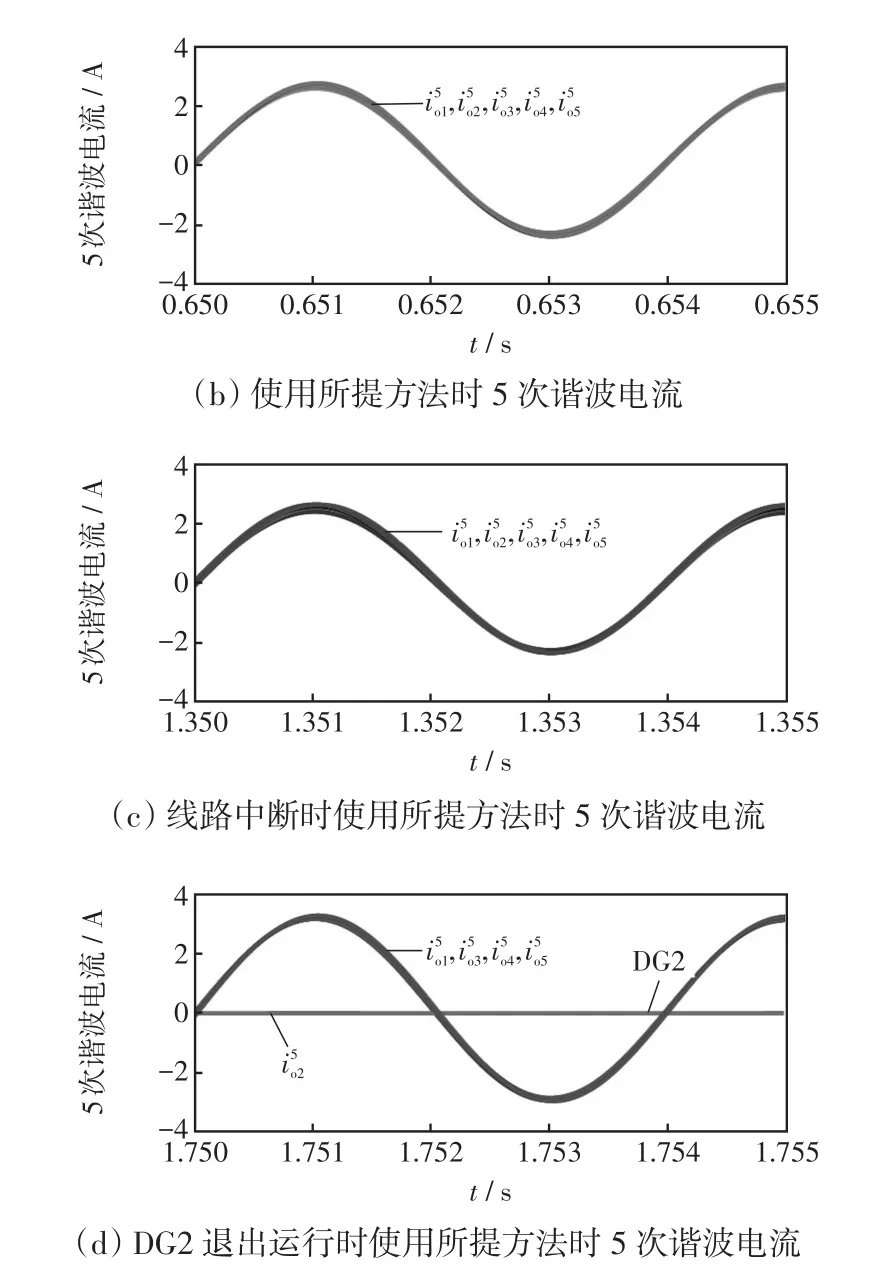
图14 线路中断和DG退出时施加所提控制方法前后谐波电流仿真波形Fig.14 Simulation waveforms of harmonic current when line is interrupted and DG plugs out before and after using the proposed method

5.4 存在通讯延时情况

本部分验证所提控制方法在存在通讯延时的情况下的有效性。根据文献[25-26]，当且仅当通讯延时时间τ满足0<τ<π/(2λmax(L))时，基于一致性算法的分布式控制仍可以达到全局渐近稳定，其中λmax(L)表示拉普拉斯矩阵的最大特征值。在仿真中，分别考虑10 ms和20 ms通讯延时，图15和图16分别为通讯延时10 ms情况下各台DG的谐波功率波形和谐波电流波形。图17和图18分别为通讯延时20 ms情况下各台DG的谐波功率波形和谐波电流波形。从图15～图18中可以看出，所提控制方法在存在通讯延时的情况下，依然能实现谐波的精确分配。

为了进一步验证所提控制方法的有效性，通过实验进行验证，实验结果如下。

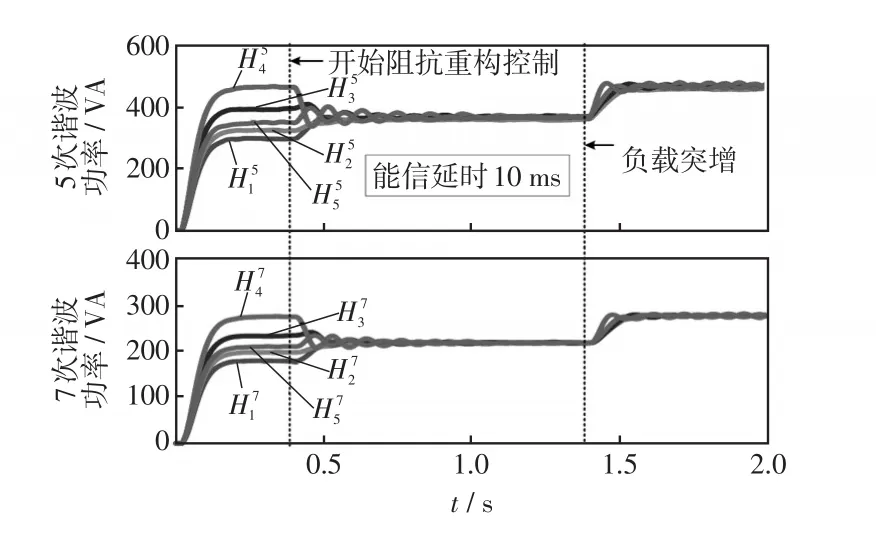
图15 10 ms通讯延时时谐波功率仿真波形Fig.15 Simulation waveforms of harmonic power with 10 ms communication delay

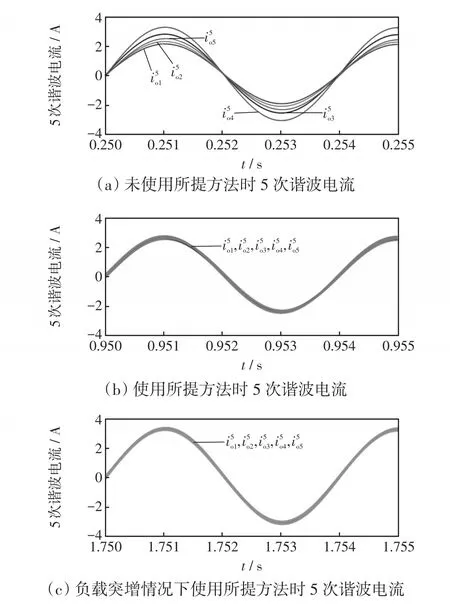
图16 10 ms通讯延时时施加所提控制方法前后谐波电流仿真波形Fig.16 Simulation waveforms of harmonic current with 10 ms communication delay before and after using the proposed method

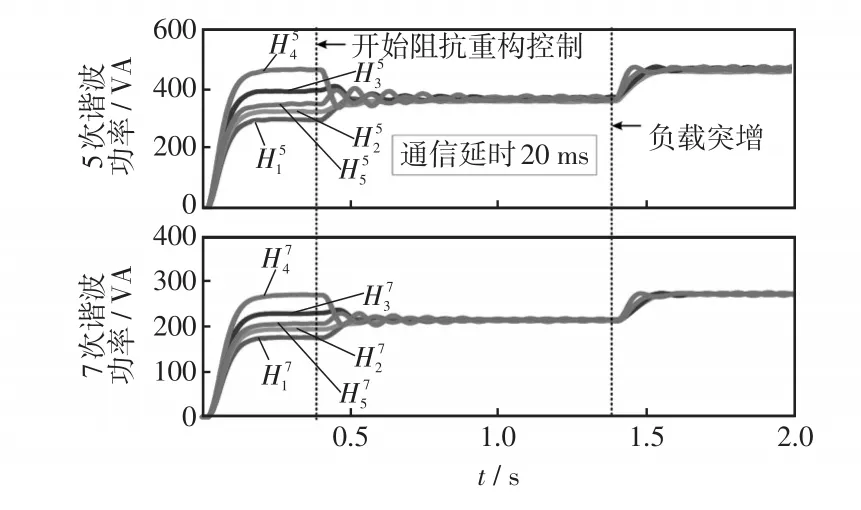
图17 20 ms通讯延时时谐波功率仿真波形Fig.17 Simulation waveforms of harmonic power with 20 ms communication delay

图18 20 ms通讯延时时施加所提控制方法前后谐波电流仿真波形Fig.18 Simulation waveforms of harmonic current with 20 ms communication delay before and after using the proposed method

施加所提控制方法前后DG的谐波电流实验波形如图19所示，图19（a）、（b）中，未施加所提方法时DG的5次谐波电流和7次谐波互不相等，差异明显。施加所提控制方法后，如图19（c）、（d）所示，此时各台DG的5、7次谐波电流都相等，消除了DG之间的5、7次谐波环流，实现了谐波电流精确均分。

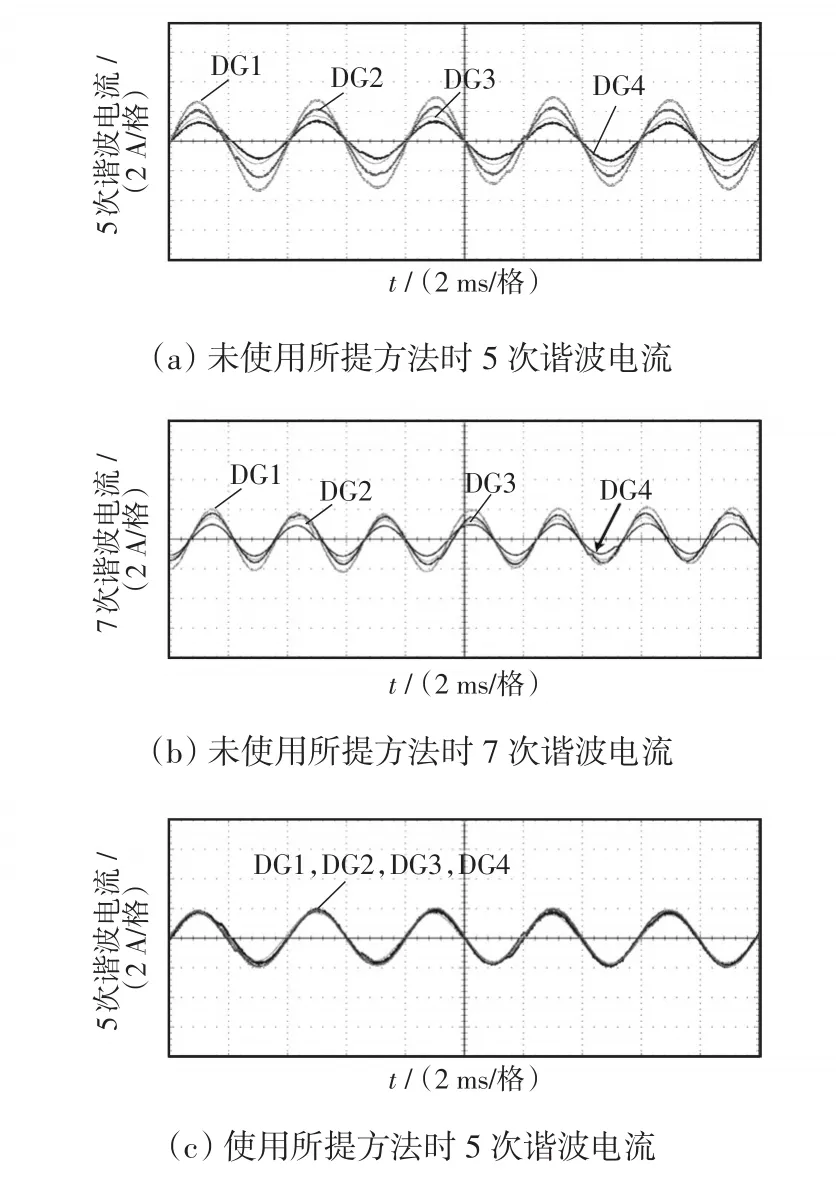
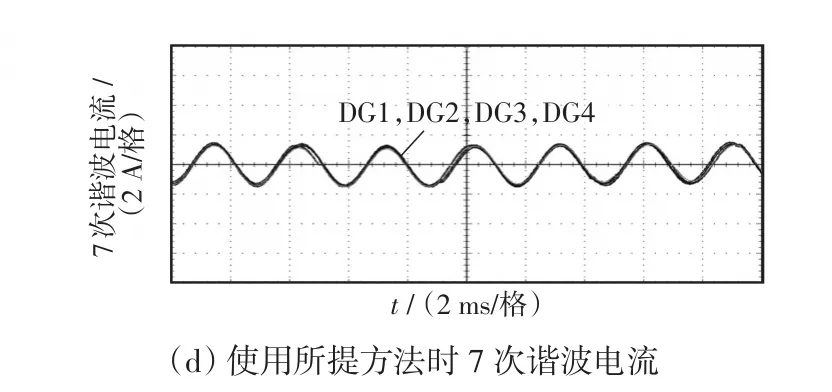
图19 施加所提控制方法前后DG的谐波电流实验波形Fig.19 Experimental waveforms of DG’s harmonic current before and after using the proposed method

施加所提控制方法前后电压THD的实验结果如图20所示。图20（a）中，未使用所提方法时电压波形质量较差，电压畸变率为6.4%，电压中5、7次谐波含量较高。施加所提控制方法后，电压波形质量得到较大改善，如图20（b）所示，此时电压中的5、7次谐波含量显著降低，电压畸变率降低为2.6%，如图21（b）所示。经过实验验证，表明所提控制方法能够提高谐波均分精度，并同时改善微电网的电压质量。

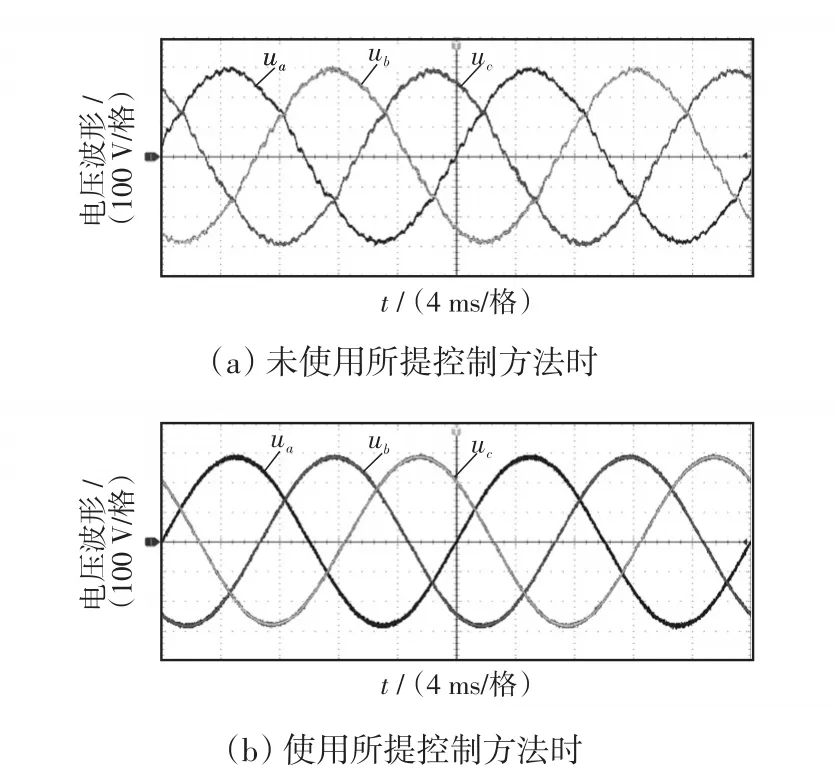
图20 施加所提控制方法前后电压的实验波形Fig.20 Experimental waveforms of voltage

图21 施加所提控制方法前后电压THD的实验结果Fig.21 Experimental results of THD of voltagebefore and after using the proposed method

6 结论

（1）通过给DG分配可变的重构因子Gh，可减小等效谐波阻抗，提高谐波均分精度，并改善微电网电压质量。

（2）所提控制方法采用分布式控制，通信故障不会影响谐波均分性能，且所提控制方法更具有广泛的通用性，能够适用于含复杂拓扑结构、结构变化的微电网。