基于轨迹灵敏度的DFIG直流过电压优化

李生虎，赵启锐，朱争高，陈 东

（合肥工业大学电气与自动化工程学院，合肥 230009）

双馈感应发电机DFIG（doubly-fed induction generator）定子电压下降，引起两侧有功不平衡，导致直流过电压[1-3]。国标《风力发电机组双馈式变流器第2部分：试验方法》规定[4]，直流电压高于阈值，变流器应立即停机。为避免直流过电压，可以采取以下措施：采用转子撬棒时，转子侧变流器RSC（rotor-side converter）被隔离，DFIG失去有功控制能力且需吸收无功。直流撬棒[5]和储能[6-7]可稳定直流电压。在定子外侧接可控并补或串联阻抗，可以提高定子电压，降低直流过电压。硬件电路需要增加成本。

调整桨距角或转速，减小捕捉风能，有助于直流回路有功平衡，但响应速度慢。文献[8]建立了Lyapunov函数，把补偿项反馈至网侧变流器GSC（grid-side converter）控制，减小不平衡功率；文献[9]改进GSC控制为单环控制；文献[10]增加前馈补偿；文献[11]采用直流电流单闭环控制、取消延时补偿，以抑制直流电压峰值；文献[12]协调RSC与GSC控制，取得较好效果。

增大电容可以抑制直流电压波动，但将降低控制灵活性和故障后恢复速度。文献[13]采用粒子群算法优化DFIG控制参数，但是计算效率较低；文献[14]引入特征灵敏度算法优化控制参数，适合稳态运行方式，不能反映故障严重程度和持续动态过程。轨迹灵敏度可求解一段时间内系统运行参数或者性能指标对某个控制参数的灵敏度。以此为一阶梯度，可以优化控制参数，改善系统动态性能。采用轨迹灵敏度算法，文献[15]辨识DFIG动态参数，文献[16]进行电压优化控制，文献[17]量化电网暂态稳定性，文献[18-19]优化设计同步发电机PSS参数，文献[20]优化DFIG参与调频的控制参数。目前未见将轨迹灵敏度引入DFIG直流电压的研究，其难点在于：①轨迹灵敏度可由摄动法或解析表达得到。前者容易实现，但是需要两次时域仿真，计算量大，且每次只能得到一个参数的轨迹灵敏度。后者更为直接实用，但是需要建立严格推导过程。目前未见相关轨迹灵敏度的解析表达。②基于轨迹灵敏度的控制参数排序选择[21]，一般基于平均相对灵敏度指标[22]，灵敏度较大设置为备选参数[23]。但是平均灵敏度不能反应动态过程中运行参数越限情况。因此针对DFIG直流过电压问题，需要改进评估指标。③为抑制直流过电压，最简单方法是增大直流电容，但是这不仅需要增加成本，还将减缓故障后恢复速度，因此最好协调其他参数，在满足直流电压安全前提下，减小直流电容。因此需要以评估指标为判据，筛选控制参数。

本文针对电网故障后电压下降导致DFIG直流过电压问题，建立轨迹灵敏度解析表达，大大减小算法工作量，并提出峰值相对轨迹灵敏度指标以确定控制直流电压备选参数，使得所提指标对于传统指标的选参更为准确。综合直流电压控制和直流电容成本建立目标函数，通过轨迹灵敏度提取梯度信息，采用BFGS算法近似得到海森矩阵，建立参数优化算法。算例结果比较了不同备选参数和目标函数下对直流电压峰值和恢复速度的控制效果，验证了所提算法的应用价值。

1 DFIG直流电压

1.1 DFIG动态建模

图1和图2为DFIG结构和控制模型，图中，Vs、Is、Vr、Ir、Vg、Ig分别为定、转子和GSC电压、电流，Vdc为直流电压，Ps、Qs为定子出力，Pg、Qg为GSC注入定子功率，PDFIG、QDFIG为DFIG注入电网功率。Lss、Lrr分别为定子、转子自感，Lm为激磁电感。按定子电压定向，下标d-q表示对应变量d-q轴分解值，上标*表示参考值。由风速vw和桨距角β通过cp函数得捕获功率。RSC和GSC采用功率外环和电流内环控制。基于文献[24]改进平电压启动方法，可求解DFIG初值。

图1 DFIG结构Fig.1 Structure of DFIG

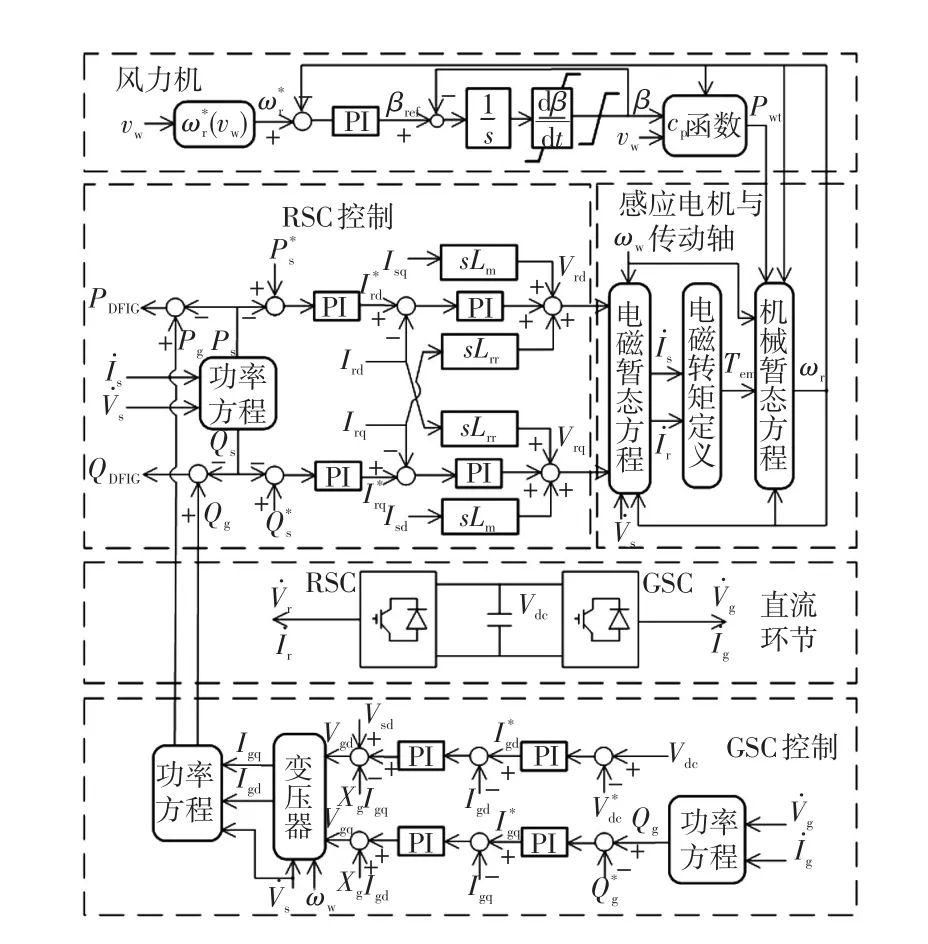
图2 DFIG动态控制Fig.2 Dynamic control of DFIG

1.2 直流电压方程展开

2 DFIG直流电压轨迹灵敏度的解析表达

2.1 轨迹灵敏度解析表达

2.2 轨迹灵敏度评估指标

3 DFIG直流电压控制优化

图3给出DFIG直流过电压抑制的参数优化流程。

图3 抑制DFIG直流过电压的参数优化Fig.3 Parameter optimization against DC overvoltage of DFIG

4 算例仿真

基于所提模型，编写Matlab程序。DFIG容量为 1.5 MW，其他参数见文献[14，20，24]。风速为11 m/s，在0.2 s时并网点电压跌至70%，0.4 s时恢复，取仿真步长0.001 s。

4.1 基于相对轨迹灵敏度评估指标的主导参数选择

由式（6）～式（9）得到Vdc对Cdc和PI参数的轨迹灵敏度。计算0.2～2.0 s期间平均相对轨迹灵敏度和峰值平均相对灵敏度见表1，排序见表2。对Vdc影响较大参数为Cdc、kpg1、kpr3、kpr4、kig1，将其设为备选参数。

表1 基于轨迹灵敏度分析的评估指标Tab.1 Evaluation indices based on trajectory sensitivity analysis

表2 基于评估指标的参数排序Tab.2 Parameter sorting based on evaluation indices

直流电压及其相对轨迹灵敏度如图4所示。图4（a）中Vdc在0.439 s时峰值大于阈值。由图4（b）～（f）的相对轨迹灵敏度发现Vdc对kpg1轨迹灵敏度波动最大，对其平均相对轨迹灵敏度也最大，但在t(p)处相对轨迹灵敏度小于对Cdc灵敏度，因此kpg1对Vdc波动调节效果优于Cdc，但降低峰值能力弱一些；kpr3、kpr4、kig1比Cdc和kig1相对灵敏度偏小；kig1在t(p)时相对灵敏度小，在t(p)之后灵敏度大，故平均值较大，但对Vdc,max调节效果弱于kpr3和kpr4；比较t(p)时刻结果，减小kpg1、Cdc、kig1或者增大kpr3、kpr4，可以抑制Vdc,max。

图4 直流电压及其相对轨迹灵敏度Fig.4 DC voltage and its relative trajectory sensitivity

图5给出了对备选参数分别调节10%后Vdc曲线，按效果排序为：Cdc，kpg1，kpr3，kpr4，kig1。以Cdc调节效果为基准，kpg1、kpr3、kpr4、kig1抑制效果为72%、51%、24%、14%。因此Lˉ可以大致选择备选参数，但不能反映对Vdc抑制效果。Lp能选择出备选参数且可以反映效果。因此分别选择Cdc、kpg1、kpr3为待优化参数。

图5 参数调节前后直流电压Fig.5 DC voltage before and after parameter adjustment

4.2 参数优化对比与直流电压抑制效果分析

取Cdc、kpg1、kpr3范围分别为[0.01，0.30]F、[0.333，0.1001]、[0.135，0.405]，权重系数分别为0.999 99和0.000 01。设计方案1：无优化；方案2：优化kpg1、kpr3；方案3：优化Cdc；方案4：优化Cdc、kpg1、kpr3。优化前后对Vdc的控制效果见图6。可见：方案1时Vdc,max最高；方案2的Vdc峰值被抑制但不满足阈值；方案3和4中Vdc满足阈值；方案3比方案4的Vdc更低，因为优化后Cdc更大，抑制了Vdc升高，但是方案3抑制了故障切除后Vdc的恢复速度。

图6 参数优化对直流电压控制效果Fig.6 Control effect of parameter optimization on DC voltage

表3给出优化前后参数。方案2：Cdc不变，kpg1增大，kpr3减小。方案3：kpg1、kpr3不变，Cdc增加约4倍。方案4：kpg1、kpr3与方案2相同，但Cdc增加约2.6倍，可以看作方案2的进一步优化。方案4的Cdc比方案3减少39%。比较可见，综合目标函数在降低Vdc同时，减小了Cdc，节约了成本。

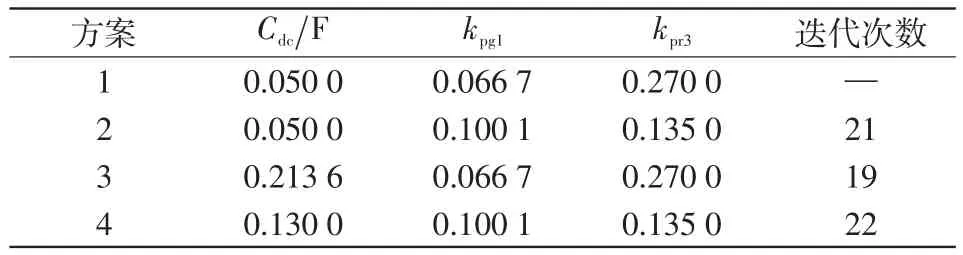
表3 优化前后参数Tab.3 Parameters before and after optimization

采用方案3和4，图7给出0～20 s的Vdc仿真结果。在实现相同抑制效果前提下，相比方案3，方案4的Vdc波动幅度减小，恢复速度增加，效果更好。

图7 2种优化方案下的直流电压Fig.7 DC voltage under two optimization schemes

以暂态过程直流电压与其稳态值偏差绝对值积分为电压波动指标，根据电压波动范围小于±5%对应时间来评估恢复速度，结果如表4所示，方案4比方案3直流电压波动减少36%，恢复时间减少2.132 s。

表4 方案3和4的直流电压波动及恢复时间Tab.4 DC voltage fluctuation and recovery time under Schemes 3 and 4

5 结论

为避免DFIG直流过电压，本文定义峰值相对轨迹灵敏度指标，基于轨迹灵敏度优化直流电容和变流器参数，得到以下结论：

（1）为选择抑制直流过电压的参数，峰值相对轨迹灵敏度比平均相对轨迹灵敏度指标更为有效；

（2）DFIG直流电容、RSC有功内环比例系数和GSC电压外环积分系数，对Vdc抑制效果更明显；

（3）采用综合目标函数，可以协调变流器参数和直流电容成本。与只优化Cdc相比，同时优化Cdc和变流器参数，Cdc减少39%，Vdc波动减小36%，恢复时间减少2.132 s。

将本文算法拓展至风电并网电力系统，当参数较多或参数变化范围较大时，协调控制难度增加，有待进一步研究。