装配式H型钢防屈曲支撑的疲劳寿命计算方法★

金晓飞,韩 伟,崔婧瑞,李 伟

(1.中国建筑一局(集团)有限公司，北京 100161；2.北京堡瑞思减震科技有限公司，北京 100160; 3.烟台大学土木工程学院，山东 烟台 264005)

1 概述

我国自古以来便是地震多发国家，随着经济社会的发展，地震灾害带来的经济损失呈现出非线性加速增长的趋势。传统的抗震设计方法主要通过加大构件截面尺寸和配筋来“硬抗”地震，上述技术手段能够有效提升主体结构的刚度和抗震能力，但同时也增加了设计地震荷载，抗震设计成本和震后修复代价较高。耗能减震是提高工程结构抗震能力的新兴技术手段，通过布置耗能减震装置吸收地震能量，耗能减震结构可以实现地震作用下主要结构构件始终处于弹性工作阶段，进而保证主体结构具有可靠的抗震韧性。因为具有理念先进、经济合理等特点，耗能减震技术目前正得到越来越广泛的认可和应用[1]。在众多耗能减震装置中防屈曲支撑因具有取材方便、力学性能稳定等优点而备受青睐[2]。防屈曲支撑主要通过钢质耗能内芯的弹塑性变形来耗散地震能量，钢材进入弹塑性阶段后会存在残余变形，同时在往复荷载作用下防屈曲支撑还有可能发生疲劳破坏。为了便于震后检测、维护以及更换，一种装配式H型钢防屈曲支撑被提出。本文主要基于已有的试验结果结合理论分析，提出不同构造形式下装配式H型钢防屈曲支撑的疲劳寿命计算方法，从而为该类防屈曲支撑在实际工程应用过程中检修及更换周期的制定提供理论和技术支持。

2 装配式H型钢防屈曲支撑的基本构造

为了能够在有限的空间内提供较大的屈服承载力同时便于震后检测和维护，一种装配式H型钢防屈曲支撑被提出[3]。该类防屈曲支撑的耗能内芯为H型钢，约束构件为两块盖板和两个U型钢通过垫块和高强度螺栓组装而成，如图1所示。针对装配式H型钢防屈曲支撑的力学性能已经开展过系列研究[4-5]，研究表明由于约束构件能够对H型钢内芯腹板和翼缘进行全面有效约束，所以该类防屈曲支撑能够有效避免H型钢内芯过早发生弹塑性局部失稳，进而具有优异的力学性能稳定性。

3 构造形式对疲劳寿命的影响

研究发现，构造形式会对装配式H型钢防屈曲支撑的疲劳性能产生明显影响。参考文献[4]中试件S3和S4分别为耗能内芯无、有中间限位装置的装配式H型钢防屈曲支撑，上述两个试件H型钢内芯的基本构造如图2所示。试验研究表明：耗能内芯不设置中间限位装置时，试件S3加工及组装方便，但工作过程中会在耗能内芯一端出现严重的变形集中现象，从而对防屈曲支撑的疲劳性能产生不利影响；试件S4设置有截面均匀过渡的中间限位装置时，H型钢内芯端部的变形集中现象能够得到显著减轻，进而有利于内芯钢材疲劳性能的充分发挥，但试件的加工成本会有所增加。基于上述研究成果，本文主要通过理论分析结合已有试验数据，分别提出无、有中间限位装置情况下装配式H型钢防屈曲支撑的疲劳寿命计算方法，从而推动和促进该类防屈曲支撑在不同工程需求背景下的实际应用。

4 疲劳寿命计算方法

装配式H型钢防屈曲支撑主要通过耗能内芯的弹塑性滞回变形耗散外部输入能量，在循环往复荷载作用下钢质的H型钢内芯会因损伤累积而发生疲劳破坏。作为结构中重要的抗侧力构件，防屈曲支撑一旦发生疲劳断裂会直接影响整体结构的抗震性能并有可能增加整体结构的脆性破坏倾向，所以能够可靠地预测装配式H型钢防屈曲支撑的疲劳寿命对该类防屈曲支撑的设计、使用、维护以及更换标准的制定具有重要的理论和实际意义。

4.1 基于内芯材料的疲劳寿命计算方法

已开展的试验研究中H型钢内芯的钢材牌号均为Q235，Q235钢材的疲劳寿命计算公式如式(1)所示[6]。

εa=0.003×(2Nf)-0.08+0.155 9×(2Nf)-0.462

(1)

其中,εa为总应变幅值；Nf为与εa相应的疲劳寿命。

循环往复荷载作用下，防屈曲支撑的疲劳破坏可以根据损伤累积法则进行判定，如式(2)所示。

(2)

其中，D为损伤累积系数；Di为第i个加载幅值下的损伤因子；ni，Nfi分别为第i个加载幅值下的实际加载圈数和理论疲劳寿命，当D=1时试件发生疲劳断裂。

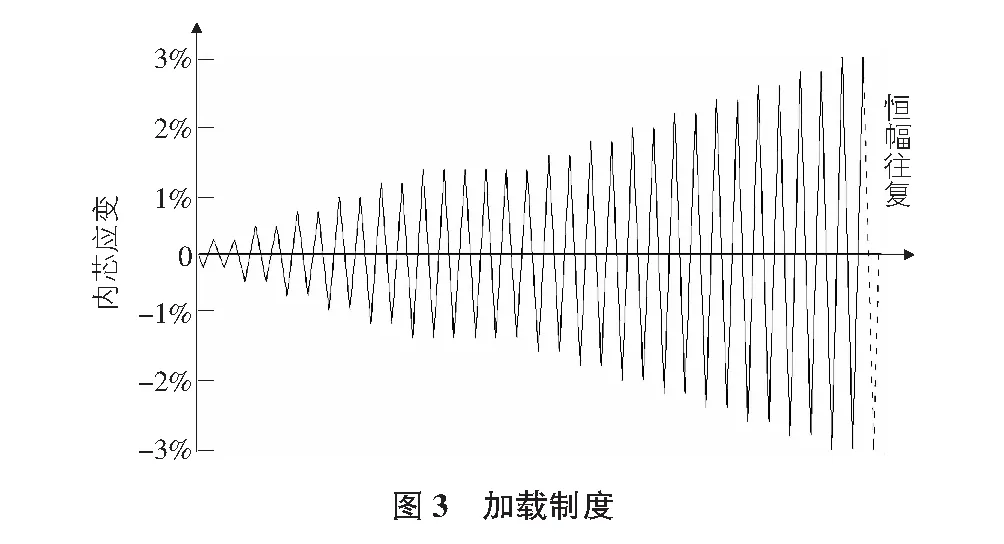
对试件S3和S4进行试验研究时采用了拟静力滞回加载，加载过程包括弹性和弹塑性两个阶段：弹性阶段采用力控制加载，荷载幅值为0.5倍屈服荷载预估值，循环加载4圈；弹塑性阶段采用位移控制加载，内芯应变从0.4%开始以0.2%的增幅递增至3%，除应变1.4%处往复加载6圈外，其余每一级均循环加载2圈，最后在内芯应变3%处循环加载直至试件疲劳断裂，如图3所示。

试件S3和S4的滞回曲线分别如图4，图5所示，其中试件S3在内芯应变±2.2%处循环加载至第2圈发生疲劳断裂，而试件S4的极限应变达到±3%，加载2圈后失效。

由于弹性加载阶段应力幅值较小且仅加载4圈，对防屈曲支撑的疲劳性能影响有限，所以本文主要基于弹塑性阶段的加载历程对试件S3和S4进行疲劳寿命的分析与计算，两个试件各位移幅值下的实际加载圈数ni,基于式(1)计算而得的疲劳寿命圈数Nfi以及损伤累积系数D的计算结果如表1所示。

基于表1的计算结果可以发现，试件S4的累积损伤系数明显高于S3，证实了设置中间限位装置有利于延长装配式H型钢防屈曲支撑疲劳寿命。同时还可以发现，试件S3和S4均在损伤累积系数远小于1的情况下提前发生了疲劳断裂，其主要原因在于：首先，式(1)是基于无屈曲钢板轴向拉压疲劳寿命试验结果通过数据拟合而得，然而防屈曲支撑在实际工作过程中其耗能内芯并不是理想的轴向受力而是会发生微幅的多波屈曲[7-8]，多波屈曲会产生附加弯曲应变，进而导致防屈曲支撑耗能内芯实际工作过程中的应变幅值会明显大于名义轴向应变幅值[9-10]。除此之外，防屈曲支撑耗能内芯加工过程中的焊接残余应力以及变截面导致的应力集中也会对防屈曲支撑的疲劳性能产生不利影响，而式(1)也并未对上述因素加以考虑。正是由于上述原因，直接采用式(1)进行计算会高估装配式H型钢防屈曲支撑的疲劳寿命进而给主体结构带来潜在的安全隐患，所以有必要针对性提出装配式H型钢防屈曲支撑的疲劳寿命计算方法，以保证该类防屈曲支撑在实际工程应用中的安全性和可靠性。

4.2 修正后疲劳寿命计算方法

定义装配式H型钢防屈曲支撑疲劳损伤修正系数β为损伤累积系数的倒数，如式(3)所示。则基于表1中的计算结果可得对于无中间限位装置的试件β=4.840，而对于有中间限位装置的试件β=1.938。之后，将疲劳损伤修正系数β引入式(1)可得无、有中间限位装置时装配式H型钢防屈曲支撑的疲劳寿命计算公式分别如式(4)和式(5)所示。

β=1/D

(3)

εa=0.003×(9.68·Nf)-0.08+
0.155 9×(9.68·Nf)-0.462

(4)

εa=0.003×(3.876·Nf)-0.08+
0.155 9×(3.876·Nf)-0.462

(5)

基于式(4)和式(5)对试件S3和S4重新进行计算校核，结果如表2所示，可以发现此时试件S3和S4均在损伤累积系数D接近1时发生疲劳断裂，从而证明式(4)，式(5)结合损伤累积法则可以较为准确地预测无、有中间限位装置时装配式H型钢防屈曲支撑的疲劳寿命。

需要特别指出的是，间厚比(耗能内芯与约束构件之间的总间隙值与耗能内芯厚度之比)是影响防屈曲支撑疲劳寿命的一个关键因素，间厚比越大耗能内芯受压时多波屈曲产生的附加弯曲应变越大，在相同名义位移幅值下防屈曲支撑的疲劳寿命相应也就越低。对于装配式H型钢防屈曲支撑，试验结果显示所有试件最终的疲劳断裂均起源于H型钢内芯翼缘，所以在对装配式H型钢防屈曲支撑进行疲劳寿命分析和计算时应重点考虑H型钢内芯翼缘间厚比的影响。试件S3和S4翼缘厚度实测值为7.1 mm，翼缘和约束构件之间的总间隙值为3.5 mm，所以本文所提的疲劳寿命计算公式适用于翼缘间厚比约为0.49的装配式H型钢防屈曲支撑，对于其他间厚比情况，则仍需通过进一步的理论和试验研究以确定相应的疲劳寿命计算公式。

表2 修正后试件S3和S4损伤累积系数计算

5 结论

本文以一种装配式H型钢防屈曲支撑为研究对象，基于已有试验结果结合理论分析，提出了不同构造形式下该类防屈曲支撑的疲劳寿命计算方法，从而为该类防屈曲支撑的实际工程应用提供理论和技术支持。本文主要结论如下：1)设置截面均匀过渡的中间限位装置能够有效提高装配式H型钢防屈曲支撑的疲劳寿命。2)采用内芯材料疲劳寿命计算公式会高估装配式H型钢防屈曲支撑的疲劳寿命，进而给工程结构带来潜在安全隐患。3)基于本文所提的修正后疲劳寿命计算公式结合损伤累积法则可较为准确地预测装配式H型钢防屈曲支撑的疲劳寿命。