基于稀疏自动编码器和支持向量机的矿渣立磨主减速机故障预警研究①

朱 全, 纪 萍, 黄 鲁, 韩飞坡

(1.马鞍山学院智造工程学院,安徽 马鞍山 243100;2.皖江工学院电气信息工程学院,安徽 马鞍山 243031)

0 引 言

矿渣立磨是矿渣微粉生产的关键设备,其核心部件包括主电机、主减速机、基座、磨盘、压辊、齿式联轴器、选粉机等。主电机和主减速机通过齿式联轴器接合,将主电机的输出转矩传输至主减速机,再经主减速机将主电机的高速小转矩转换为低速大转矩,用以驱动磨盘及其之上的磨辊,实现立磨对矿渣的研磨。由于立磨是多输入、强耦合、强阻抗、大功率、非线性的系统,全部动力均来自主电机和主减速机,在立磨的工作过程中,主电机、主减速机承担着非常大的负荷。立磨主减速机在主电机和磨盘之间传递功率和转矩,同时受到立磨内部复杂工况的影响,在工作中起着举足轻重的作用,是整个立磨设备的“心脏”,其运行之平稳、性能之优劣,直接影响到立磨的正常工作。

目前,已有部分国内外学者对立磨主减速机的故障做了若干研究,文献[1]提出利用小波变换对矿渣立磨主减速机进行故障诊断,文献[4]使用扭矩信号检测与诊断立磨减速机的故障。上述方法有其局限性,小波变换具有很好的时域局部化能力,能够有效提取瞬时频率,然而产生的时频描述比较模糊,降低了瞬时幅度的可读性;使用扭矩信号只能检测到立磨即时故障,对于设备的故障隐患却无法检测。

1 矿渣立磨主减速机概述

立磨主减速机作为动力承接转换设备,对减速机的制造装配精度和设备安装、使用维护要求较高,在实际生产中主减速机的故障率远高于其他设备,经分析研究,主要是以下几个方面的原因:1)受限于国内的加工制造装配水平,国产主减速机制造装配存在一定误差;2)主减速机安装要求较高,例如:对于基座安装面的平面度要求小于0.2mm,主电机输出轴和主减速机输入轴同轴度要求控制在0.5mm以内,超差的安装将引起故障隐患;3)主减速机长期在高负荷下工作,且工作条件复杂,使用维护不当容易引起材料的疲劳失效。

以3000k W矿渣立磨主减速机为例,说明该减速机的结构原理,如图1所示[1]。立磨主减速机位于立磨的正下方,磨盘安装在其顶部,与减速机输出端相连接。磨盘重力和磨辊压力由主减速机的推力轴瓦承担,减速机内部传动机构负责传递功率和转矩。

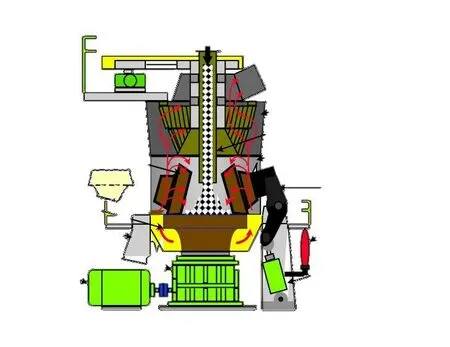
图1 立磨结构简图

减速机传动机构是由一级伞齿和两级行星齿轮组成的三级减速结构,如图2所示[3]。输入端为锥形伞齿,一级太阳轮为双连齿轮,浮动齿套与锥形伞齿啮合,同时与一级行星轮、一级齿圈组成一级行星轮系,该轮系的输出为行星轮架,同时作为二级太阳轮的输入,与二级行星轮和二级齿圈组成二级行星轮系,二级行星轮架作为减速结构的输出端,用以驱动磨盘转动。通过两级行星轮系传动可以使整体结构紧凑,减小设备体积和重量,同时可以增大传动比,且传动效率高,容易实现大功率传输。

图2 主减速机传动简图

立磨主减速机的故障主要由齿轮、轴及轴承所引起。齿轮引起的故障主要是轮齿失效引起的,包括轮齿折断、齿面磨损、齿面点蚀、齿面胶合、塑性变形等;轴引起的故障主要是轴发生失衡、塑性变形、疲劳失效等;轴承引起的故障主要有磨损和表面损伤。

2 故障预警原理

2.1 小波包构造能量特征向量

小波包是从小波变换延伸出的一种对信号进行细分和重构的方法。在小波变换中,只对低频部分作分解,对高频部分不再分解,因此高频部分的分辨率较差,容易造成信息丢失。小波包在小波变换的基础上,不仅对低频部分分解,对高频部分也可进行分解,提高了信号处理的分辨率。分解后的系数具有能量的量纲,各个频带的能量表征了不同的故障状态,所以可提取能量特征向量作为故障诊断的依据。小波包定义如式(1):

设|h k|及|g k|(k∈Z)是一对正交镜像滤波器(QMF),定义递归函数

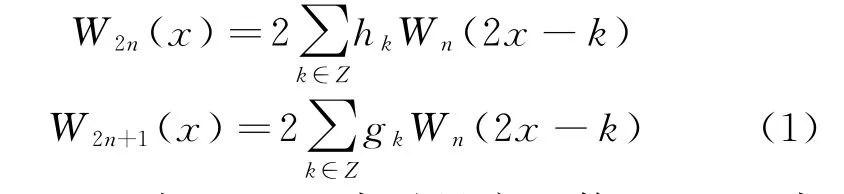
当n=0时,W0(x)表示尺度函数,W1(x)表示小波基函数。从信号分析的角度不难看出,小波包分解将信号分别通过高通滤波器和低通滤波器进行滤波,对高频部分和低频部分再次进行滤波,经过若干层的分解,信号的高频部分和低频部分被逐步细化。

以三层小波包为例,信号经过滤波分解后,得到含有8个频带成分的特征信号,如图3所示。每个节点可用(i,j)来表示,i表示分解层数,j表示该层第j个节点。

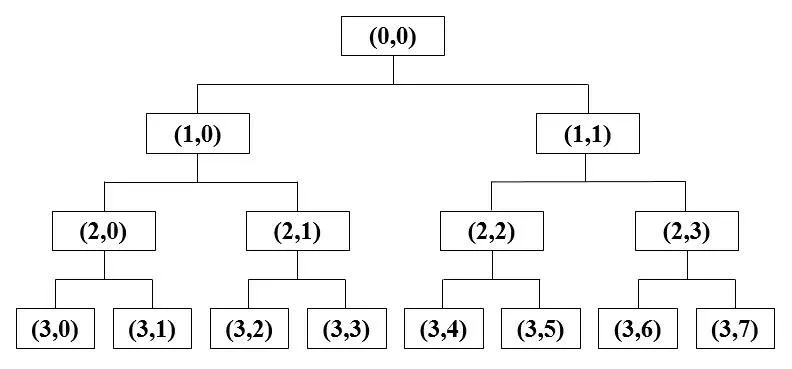
图3 三层小波包分解图

根据Paseral恒等式,小波包系数具有能量的量纲,可将其用于能量分析。主减速机带有故障时振动信号各频带内的能量有明显差异,不同故障对各频带内的能量影响也各不相同,所以可提取各频带内的能量构造特征向量。步骤如下:

(1)对振动信号进行三层小波包分解,将信号分解到从低频到高频八个频带内,以S3j(j=0,1,…,7)表示各频带信号。

(2)计算各频带信号能量,用E3j(j=0,1,…,7)表示各频带对应的能量,有式(2):

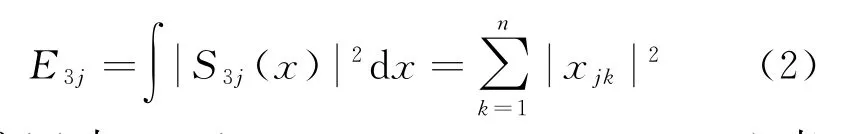
式(2)中,x jk(j=0,1,…,7;k=0,1,…,n)表示各频带信号S3j在离散点的幅值,n为采样点数。

(3)以各频带内的能量为元素构造特征向量,以T表示能量特征向量,有式(3):

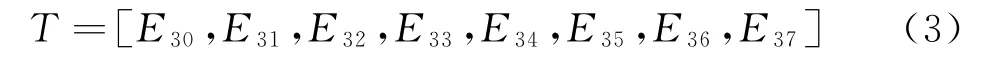
该向量中能量元素数值较大,对此可作归一化处理,如式(4):

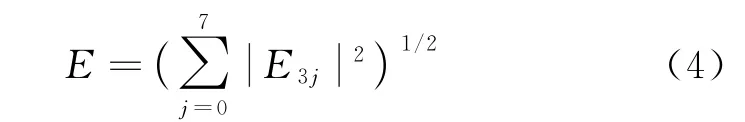
用E分别除特征向量的各元素,得到归一化的特征向量。

2.2 稀疏自动编码器

稀疏自动编码器(SAE)是以自动编码器(AE)为基础的神经网络。自动编码器是一种无监督的神经网络,其原理是输入数据经过编码器,得到输出数据,再反向通过解码器对输入数据进行重构,经过多次循环迭代调整解码器,可以最小化输入数据和输出数据之间的重构误差,如图4所示。单个自动编码器模型包括输入层、隐含层、输出层,如图5所示。

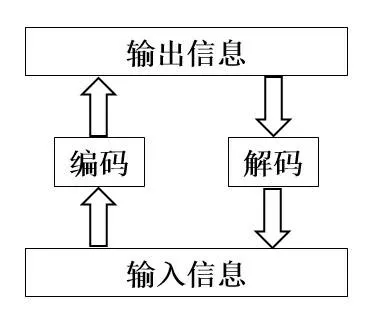
图4 自动编码器原理图

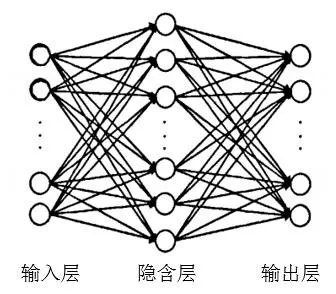
图5 单层自动编码器模型

编码器将输入数据通过激活函数映射到隐含层。设h表示隐含层,如式(5):

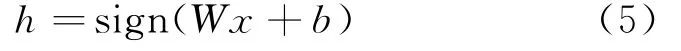
式(5)中,sign(·)为Sigmoid激活函数,W为输入层和隐含层之间的权重矩阵,x为输入信息,b为隐含层偏置。利用解码器对隐含层所得的数据进行重构,设表示重构信息,如式(6):

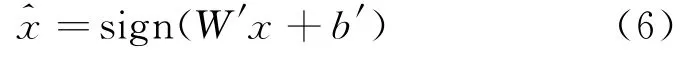
式(6)中,W'表示输出层与隐含层之间的权重矩阵,b'表示输入层偏置。

自动编码器的训练是为了在训练样本集上寻找一组最优参数集θ={W,b,W',b'},使得重构误差最小。对于S个样本的训练样本集{x1,x2,…,x S},重构误差函数定义为式(7):

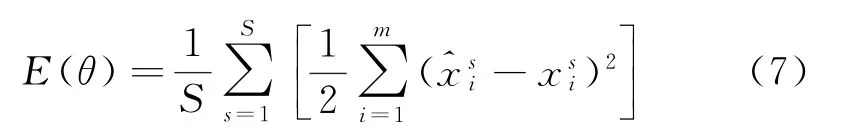
式(7)中,x s=[x s1,x s2,…,x sm]T为训练样本集中第s个样本,m为样本的维数。

自动编码器由于隐含层节点数目过多会引起学习过程中的过度完备性,采用稀疏自动编码器(SAE)予以解决。将基于KL散度的稀疏表示用于自动编码器的重构误差函数中,对于隐含层含有p个节点的稀疏自动编码器,其重构误差函数定义为式(8):

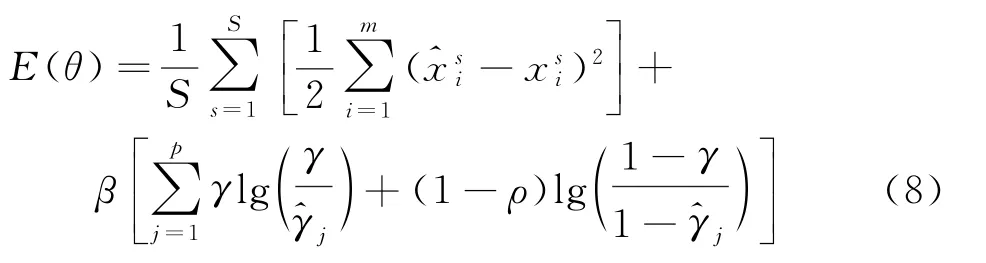
式(8)中,β为稀疏惩罚因子,γ为稀疏参数,表示隐含层节点的平均激活度,该平均激活度定义为式(9):

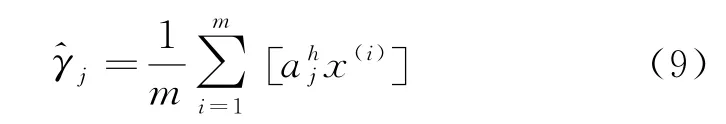
式(9)中,j表示稀疏自动编码器隐含层的第j个节点,a hj表示隐含层中第j个节点的激活值,表示第i个样本在隐含层中第j个节点的激活度。

2.3 支持向量机

为实现输入数据的分类识别,在稀疏自动编码器的顶层设计一个分类器。支持向量机(SVM)是一种以统计学习理论为基础的机器学习方法,适用于小样本情况下的快速学习。其基本思想如图6所示,不同符号表示两类样本,H为分类线,H1,H2分别为过距离分类线最近的样本且与分类线平行的界线,H1和H2之间的距离称为分类间隔,H1,H2上的样本为支持向量。所谓最优分类线就是要求分类线不但能将两类样本正确地分开,而且使得分类间隔最大。分类线可用方程表示为W·X+b=0,对其进行归一化处理,使得对于线性可分的样本集(x i,y i),i=1,…,n,x∈R n,y∈{-1,1}满足式(10):

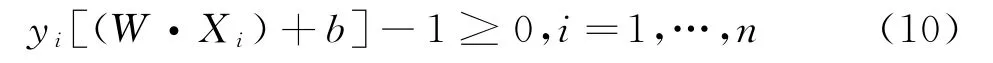
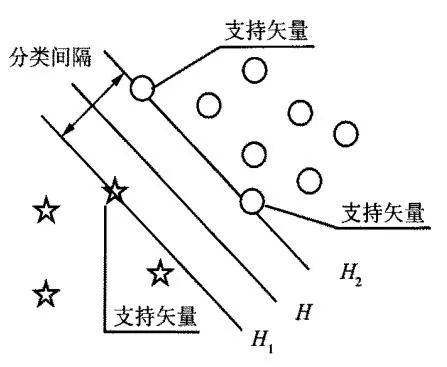
图6 线性可分的最优分类线

此时分类间隔等于2/‖ω‖,要使分类间隔最大即等同于‖ω‖2最小。利用Lagrange优化方法在约束条件和αi≥0,i=1,…n下对αi求函数Q(α)最大值,如式(11):

式(11)中,αi为与每个样本对应的Lagrange乘子。这是一个不等式约束的二次函数寻优问题,解中只有少部分αi不为零,与此对应的即为支持向量。由此得到最优分类函数

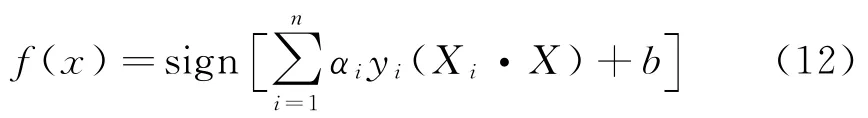
SVM最初是对二元类型分类问题提出的,而立磨主减速机的故障是多类的,对此可采用扩展的方法把多类的问题转化为两类问题,首先将其中一种类别的训练样本作为一类,其余不属于该类的训练样本作为另外一类,再对剩下的训练样本进行二元分类,确定第二种类型,依次确定所有类型。对于K类样本,要建立K个分类器,分别对应K类分类模型。分类标签用{-1,+1}表示,+1表示对应的该类模型状态,-1表示其它模型状态。对于K类模型状态的分类如表1所示。

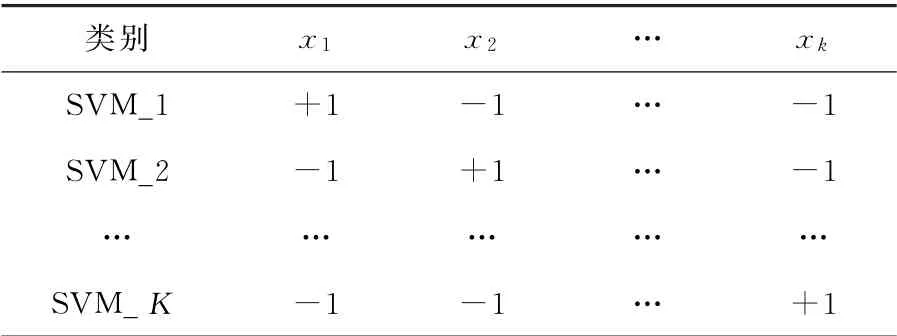
表1K类模型状态分类表

由表中不难看出,每个分类器的输出只有一个+1,每种样本在多个分类器中只对应一个+1。若是某一样本在多个分类器中输出+1,说明分类错误;若是所有分类器输出中全部为-1,说明分类错误或是出现未知的模型状态,等同于故障预警。

3 故障诊断方法和应用

针对一般故障诊断方法依赖大量数据提取故障特征的局限性,以及特征提取泛化性不强的缺点,提出了以小波包分解技术、稀疏自动编码器和支持向量机为基础的故障诊断方法,实现故障预警和分类。该方法的流程如图7所示,主要步骤如下:

图7 故障诊断流程图

(1)对若干批次的含有某种类型故障信息的原始振动信号进行三层小波包分解,提取各频带系数,构造能量特征向量,并作归一化处理,作为训练样本和测试样本。

(2)构建稀疏自动编码器,设置稀疏惩罚因子和稀疏参数,确定输入层、隐含层和输出层节点数目,初始化权值矩阵和偏置。

(3)设置前向算法的训练次数和迭代次数,将训练样本作为稀疏自动编码器的输入,执行前向计算,确定平均激活度,然后执行反向传播计算,经过多次迭代后,优化权值矩阵和偏置。

(4)将稀疏自动编码器的输出作为SVM分类器的输入对其进行训练,为验证有效性,用同类型的少样本数据对分类器训练。

(5)将测试样本数据输入故障诊断模型,根据SVM分类器的输出结果确定故障类型。

(6)对于其它故障类型,按照步骤(1)-(5)依次重复进行,最终将稀疏自动编码器和SVM分类器组成的故障诊断模型训练成为一个多重感知器,具有对输入数据进行分类的功能。

为了验证这种方法的准确性和有效性,采用凯斯西储大学提供的轴承数据进行测试。轴承数据为驱动端加速度传感器采集的振动信号,采用其中4种不同状态的轴承振动信号,分别为正常、外圈故障、内圈故障和滚动体故障,采样频率为12k Hz,电机负载为2 HP,电机转速为1750r/min,故障为用电火花加工的单点故障,点蚀直径为0.533mm。每种类型的数据各取3组,其中两组数据作为训练样本,另外一组作为测试样本,根据数据长度以10240个采样点为一个样本,每组数据取8个样本。在Matlab环境下调用小波包、稀疏自动编码器和支持向量机的相关函数进行测试和训练,训练和测试结果如图8所示。

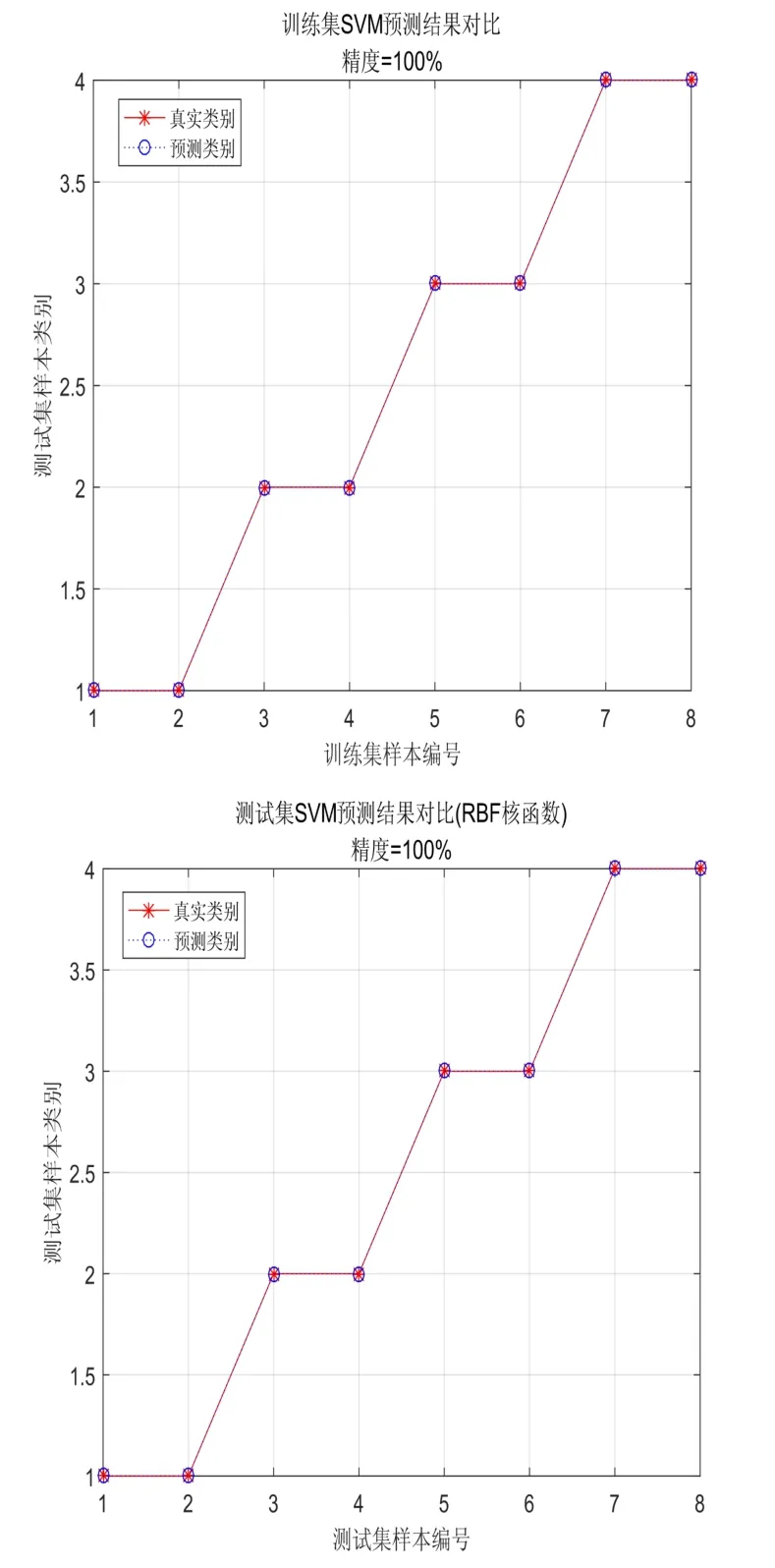
图8 故障模型训练和测试结果

根据故障模型测试结果可见,这种基于稀疏自动编码器和支持向量机的故障诊断方法可以有效地识别故障类别。利用这种方法开发一套立磨主减速机的故障预警系统,用于某钢厂的矿渣立磨主减速机。应用时须注意,由于立磨主减速机故障信号的稀缺性,在未获取该类型减速机故障样本的情况下,先将SVM分类器简化为一个二元分类器,即正常状态和非正常状态。然后利用矿渣微粉的DCS系统对立磨主减速机进行振动信号的数据采集,减速机运行时若是存在故障隐患,故障预警系统识别出非正常状态,并发出预警信号,提示对减速机进行检修,防止设备损坏加剧。确定故障类型后将采集的振动信号作为故障样本存储,为增加分类器故障类别提供依据。以这些故障样本为基础,对SVM分类器增加故障类别,经过多次迭代后逐步建立故障诊断模型,实现立磨主减速机的故障预警和故障诊断。

4 结 论

(1)利用小波包分解对减速机振动信号构建特征向量,通过稀疏自动编码器对特征向量进行数据重构,经过循环迭代调整权值矩阵,最小化重构误差,能最大程度反映出故障信息。

(2)支持向量机以稀疏自动编码器的重构数据作为输入,在小样本的情况下即可建立分类器模型,对故障可以进行准确的分类,特别适用于立磨主减速机这种故障样本数据稀缺的故障诊断。

(3)提出的方法算法简单,快速准确,为立磨主减速机这种大型设备的故障诊断提供了新的方法和依据。