一种基于认知诊断的主观题同行互评技术
许 嘉,李秋云,刘 静,吕 品,于 戈
1(广西大学 计算机与电子信息学院,南宁530004)
2(广西大学 广西多媒体通信网络技术重点实验室,南宁 530004)
3(广西大学 广西高校并行与分布式计算重点实验室,南宁 530004)
4(东北大学 计算机科学与工程学院,沈阳 110819)
E-mail:lvpin@gxu.edu.cn
1 引 言
随着大数据、云计算和互联网技术的不断发展,以Coursera、edX、中国大学MOOC和学堂在线为代表的在线教育平台的兴起给平台上的任课教师带来了严峻的教学挑战.一个最突出的教学挑战在于教师如何高效批改大规模选课学生在平台上提交的作业.鉴于做作业能够帮助学生巩固和内化知识,是至关重要的教学活动,各大在线教育平台都提供了客观题(例如选择题和判断题)的自动批改功能,减轻了任课教师的教学负担.相对于客观题,主观题(例如简答题和应用题)更能考察学生的语言表达能力、知识运用能力与创新思维能力,所以主观题的考察对于很多在线课程而言是必不可少的[1].然而,由于没有唯一标准答案,主观题的批改很难由计算机自动完成[2],需要任课教师花费大量精力逐份手工批改,导致他们无法将精力用于课程内容及活动的改进提高.可见,如何减轻任课教师的主观题批改负担是当前教育研究领域亟待解决的重要问题.
为了有效降低任课教师的主观题作业批改负担,国内外各大在线平台与科研机构提出了不少主观题评判的技术,这些技术可分为两类:基于自然语言处理的评判技术[3-5]和基于同行互评的评判技术[6-10].其中,基于自然语言处理的评判技术通过分析学生答案与教师给的参考答案之间的匹配程度来实现主观题的自动判分.然而,基于自然语言处理的评判技术通常依赖于特定领域的知识,只适用于解决面向特定领域的主观题评分问题,因此鲜有在线教育平台提供基于自然语言处理的主观题评判功能.基于同行互评的评判技术是当下不少主流在线教育平台(例如Coursera和中国大学MOOC)提供的主观题评判功能.该类技术将主观题批改任务的子集分派给每个学生,然后基于多名学生对某主观题的评分来估计该题的真实分数.基于同行互评的主观题评判技术对于教师与学生而言都有积极益处:一方面减轻了任课教师的主观题作业批改负担;另一方面要求学生评判他人的主观题作业,不但能够让他们学习到不同的解题思路,还能提高他们的课程参与度[11,12].因此,基于同行互评的主观题评判技术成为当下解决大规模主观题评判问题的主流技术和目前智能教育领域的研究热点,关注于提出提高同行互评质量的方法[13].
本文考虑基于基数估计的同行互评场景,即每名同行评价者针对每道主观题给出一个数值型的评价分数.基于同行互评的主观题评判方法的研究难点在于如何利用多个同行给出的评价分数估计被评价者的真实分数.大多数在线教育平台只是简单基于各个评价分数的均值或中位数来估计被评价者的真实分数.然而,由于同行评价者的打分质量受其可靠性、偏见等因素的影响[14],简单用各个评价分数的均值或中位数估计被评价者的真实分数往往不够准确[15].近年来,研究人员将同行评价者的评分可靠性及评分偏见作为模型的随机变量,构建了估计被评价主观题作业真实分数的概率模型,能够利用变量间的依赖关系提高估计的准确性[6-9].然而,现有研究方法均假设同行评价者的可靠性只与其当前作业的答题情况相关,未同时考虑同行评价者对主观题考察的知识点的掌握程度(由其历史答题结果数据诊断得到)对其评分可靠性造成的影响,因而存在局限性.对284名同行评价者针对三道主观题作业给出的2109条互评打分记录进行统计分析.具体而言,首先以这些同行评价者的历史答题结果数据为输入并利用流行的认知诊断DINA模型[16]诊断得到他们对主观题考察的知识点的掌握程度,并进而量化每个同行评价者对每道主观题的掌握程度值.之后,计算由每名同行评价者对每道主观题的掌握程度值组成的序列与每名同行评价者对每道主观题的评分误差值序列之间的皮尔逊相关系数.由于两个序列的皮尔逊相关系数为-0.673,表明评价者的可靠性还受其对该主观题掌握程度的影响:评价者的掌握程度越低,则平均评分误差越大,可靠性越低;评价者的掌握程度越高,则平均评分误差越小,可靠性越大.因此,在对同行评价者的可靠性进行建模时,应该同时考虑评价者对待评价习题的掌握程度信息.
鉴于此,本文提出了一种基于认知诊断的主观题同行互评技术,包括PG8和PG9两个概率模型.该技术在现有概率模型的基础上[9],同时基于同行评价者在本次作业中的答题表现(对应于本次作业取得的真实分数)以及评价者的历史答题表现(对应于基于历史答题记录诊断得到的该评价者对本次作业题的掌握程度)对评价者的可靠性进行建模,以期最终提高概率模型估计主观题作业真实分数的准确性.PG8和PG9的区别在于:PG8假设评价者的评分可靠性服从伽马分布;PG9则假设评价者的评分可靠性服从高斯分布.综上,本文的主要贡献包括:
1)提出了改进现有同行评价概率模型的思路,即应同时以认知诊断得到的同行评价者对主观题的掌握程度信息和评价者在该主观题中取得的真实分数信息作为评价者评分可靠性的建模依据,以期进一步提高概率模型对主观题作业真实分数的估计准确性.
2)基于由284名学生参与的3次主观题作业的互评活动收集真实互评数据集,并基于该数据集评估提出的互评技术和相关互评技术的有效性.实验结果表明本文提出的基于认知诊断的主观题互评技术在提高对主观题作业真实分数的估计准确性方面比其它相关技术更具优势.
本文剩余部分的内容组织如下.第2部分阐释了相关研究工作.第3部分给出了预备知识.第4部分给出了基于认知诊断的同行互评技术,包含PG8和PG9两个概率模型.第5部分为实验.最后,第6部分总结了全文.
2 相关工作
2.1 基于自然语言处理的主观题评判技术
基于自然语言处理的主观题评判技术从题目本身的特性出发,利用自然语言处理、机器学习等技术实现主观题的自动评判.例如,文献[5]基于自然语言处理技术对开放式数学问题的每一个解答转变为数字特征,再通过聚类分析发现解答中正确、部分正确以及不正确的解答结构,从而实现了对该类问题的自动判分.文献[3]针对英文论文写作题给出了自动判分的解决方案,该方案利用潜在语义分析和学习向量量化算法来提升自动判分的准确率.文献[17]针对英语简答题设计了自动判分方法,该方法利用同义词词典和衡量语义距离的两种自然语言处理方法来解决标准文本相似度衡量方法对于同义词的匹配不够准确的问题.文献[4]则基于潜在语义分析的奇异值分解策略设计了日语短文的自动评分系统.基于自然语言处理的主观题评判技术为主观题的自动评分提供解决思路,也取得了不错的评分效果.然而,该类技术通常依赖特定领域的知识来优化自然语言的处理过程,从而保证自动判分的准确性,因而只适用于解决特定领域的主观题自动判分问题,很难在其它领域推广使用.
2.2 基于同行互评的主观题评判技术
基于同行互评的主观题评判问题即让每名评价者对分配给其的一部分主观题作业进行评判,最终基于各个评价者反馈的评判信息估计每份主观题作业的质量.由于评价者的态度和能力存在差异,与众包问题类似,基于同行互评的主观题评判问题需要解决的核心问题是对评价者反馈的评价信息进行质量控制.按照评价者反馈的评价信息形式的不同,基于同行互评的主观题评价技术可分为序数(Ordinal)估计技术和基数(Cardinal)估计技术两类.
序数估计技术要求每名评价者对分配给其的主观题作业给出表征作业质量高低的排名反馈,系统则基于所有评价者给出的作业间的偏序排名信息估计每份作业的质量[18].序数估计技术通常利用基于配对比较的方法[19,20]、贝叶斯生成法[21]和矩阵分解方法[22]来估计主观题作业的质量.序数估计的方法不要求同行评价者给出主观题作业的具体分数,降低了评价者的评判难度.然而,该类技术存在两大问题[23]:首先,评价者由于评判经验有限,很难对质量相差不大的两份主观题作业给出它们的合理排序;其次,仅依赖作业间的偏序排名信息很难量化两份作业之间的质量差异.
与序数估计技术不同,基数估计技术要求每名评价者对分配给其的每份主观题作业都给出一个量化分数,系统继而基于不同评价者针对同一份作业给出的多个评价分数估计作业的真实分数.主流的基数估计方式有两种:加权求和的估计方式[23-26]和基于概率模型的估计方式[6-9].其中,加权求和的估计方式依据同行评价者的评分准确性和信任度给他们赋以不同的权重,然后以同行评价者针对主观题作业给出的评价分数为输入,通过加权求和的方法来估计该作业的真实分数.系统会根据同行评价者在新的互评活动中的评分表现来迭代更新其权重信息.另一类方式是通过构建概率模型来估计主观题作业的真实分数.本文提出的基于认知诊断的主观题互评技术就属于这类方法.这类方法的主要实现思路是将待估计的主观题作业的真实分数、同行评价者的可靠性及偏见都建模为满足一定概率分布的隐含变量,然后基于能观察到的同行评价者的评分信息来推演以上各个隐含变量的值.具体而言,Piech等人[6]首先提出了估计主观题作业真实分数的3个概率模型,即PG1(考虑了评价者当前的可靠性和偏见),PG2(在PG1的基础上考虑了评价者的历史偏见),PG3(在PG1的基础上将评价者当前可靠性设定为评价者当前作业真实分数的线性函数的随机变量).考虑到PG3模型所设置的评价者的可靠性是关于评价者真实分数的线性函数这一假设过于严格,Mi等人将评价者的可靠性建模为满足形状参数为其真实分数的伽马分布或均值为其真实分数的高斯分布,分别得到了PG4模型和PG5模型[7].研究表明一名同行评价者的评分偏见会受到其朋友的评分偏见的影响[27,28],为了提高对评价者偏见建模的准确性,Chan等人利用学堂在线平台上收集到的学生间的社交关系信息优化对评价者偏见的建模,扩展了PG1、PG4、PG5这3个概率模型[8].然而上述概率模型均认为评价者针对不同主观题作业给出的评价分数之间是相互独立的,存在局限性.因此,Wang等人在概率建模时引入了评价者的相对分数信息(即同一个评价者对不同作业评分之间的差值),提出了PG6模型(构建在PG4之上),PG7模型(构建在PG5之上)[9].这两个概率模型由于引入了评价者的相对分数信息,降低了数据稀疏性给参数估计带来的负面影响,从而有效提高了对主观题真实分数估计的准确性.然而,PG6模型与PG7模型仅基于同行评价者针对当前主观题作业取得的真实分数对其可靠性进行建模.PG6模型与PG7模型是当前最好的同行互评概率模型,实验部分将针对这两种相关模型进行比较分析.
综上,基于概率模型的基数估计方法是目前实现主观题评判的主流方法,近年来研究人员们提出了不少相关工作.然而,现有研究工作在概率建模时均未同时考虑影响同行评价者评分可靠性的两大因素,即其在本次作业中的答题表现(对应于本次作业取得的真实分数)以及其的历史答题表现(对应于基于历史答题记录诊断得到的该评价者对本次作业题的掌握程度),因而限制了它们对于主观题真实分数的估计准确性.
3 预备知识
认知诊断以认知心理学和心理计量学为理论基础,通过构建具有认知诊断功能的心理计量模型,能够基于被试的历史答题结果数据诊断其对不同技能(知识点)的掌握程度,从而为教学提供重要依据,是当下教育评估领域的研究热点[29-31].作为最流行的认知诊断模型之一,DINA模型[16]在实现对被试知识点掌握程度的精准建模的同时具有较好的解释性,近年来受到广泛的关注和研究[32,33].以同行评价者的历史答题结果数据为诊断基础,本文正是基于DINA认知诊断模型来量化评价者对主观题作业的掌握程度.
给定被试集合C={c1,…,cM},习题集合E={e1,…,eN},则记录被试和其答题结果之间关联关系的响应矩阵R可表示为R=[rmn]M×N,其中rmn=1表示被试cm答对了习题en(rmn=0则表示答错了该题).设习题集合E考察的知识点集合为KP={kp1,…,kpK},则记录习题与其考察的知识点之间关联关系的Q矩阵可表示为Q=[qnk]N×K,其中qnk=1表示习题en考察了知识点KPk(qnk=0则表示未考察该知识点).DINA模型将被试cm的知识状态描述为一个向量αm={αm1,…,αmK},称为被试cm的知识点掌握程度向量.其中,αmk表示被试cm对知识点kpk的掌握程度,且αmk∈[0,1].αmk=1说明被试cm完全掌握了第k个知识点;αmk=0则说明被试cm完全没有掌握第k个知识点.DINA认知诊断模型的项目反应函数为:
p(rmn=1|αm)=guess1-δmnn(1-slipn)δmn
(1)
其中:
δmn=∏Kk=1αmkqnk
(2)
公式(2)中,δmn表示知识状态为αm的被试cm对习题en的潜在正确作答概率,即可被定义为被试cm对习题en的掌握程度值;slipn=P(rmn=0 |δmn=1)表示被试掌握习题en考察的所有知识点但是答错该题的概率,被称为失误参数;guessn=P(rmn=1|δmn=0)指被试没有掌握习题en考察的任何一个知识点时但答对该题的概率,被称为猜测参数.DINA模型利用EM算法最大化公式(1)的边缘似然值,从而得到被试cm的知识点掌握程度向量αm.
本文假设参与主观题互评活动的同行评价者在进行主观题作业评判之前完成了该主观题考察的知识点所对应的客观题的习题练习,因而作业互评测试系统能够收集到他们对于这些知识点对应的客观习题的答题结果数据.以某同行评价者的历史答题结果数据和表征习题和主观题作业知识点间考察关系的Q矩阵为输入,利用DINA认知诊断模型即可求得该同行评价者的知识点掌握程度向量α.然后基于α和主观题作业所考察的知识点信息即可以利用公式(2)求得该评价者对于该主观题的掌握程度值.
4 同行互评概率模型
本节介绍了基于认知诊断的主观题同行互评技术,具体涉及概率模型PG8与PG9.用U表示提交主观题作业的被评价者集合,V表示参与互评的同行评价者集合.考虑到实际教学实践中一般要求提交主观题作业的被评价者都参与该作业的互评活动,因而有|U|=|V|.下面给出模型所涉及的重要概念的定义并说明它们在模型中的设定.
真实分数:假设每份被评价者提交的主观题作业对应一个真实分数,且用si表示被评价者ui∈U所提交作业的真实分数.两个概率模型中均假设变量si的取值满足高斯分布.
可靠性:可靠性(记为τv)表示同行评价者v∈V对主观题作业的评分精度.评价者v的可靠性实际反映了v给出的主观题作业的评价分数基于其偏见bv修正后的分数与主观题作业真实分数之间的接近程度.给定某主观题作业,本文首先假设评价者v对于该作业的评分可靠性τv满足形状参数为θ1δv+θ2sv的伽马分布,得到PG8模型;其次假设τv满足均值为θ1δv+θ2sv的高斯分布,得到PG9模型.其中,δv表示基于DINA认知诊断模型得到的评价者v对该作业的掌握程度.可见,PG8和PG9在对评价者可靠性建模时同时考虑了评价者的对当前作业答题表现(对应θ2sv部分)和评价者的历史答题表现(对应θ1τv部分).
偏见:偏见(记为bv)是量化同行评价者v∈V评分时表现出其评分高于真实分数或其评分低于真实分数的常量.考虑到互评活动中不同的同行评价者的偏见不同(有些给分偏高,有些则给分偏低),因此两个概率模型均认为所有评价者的偏见值的均值为0,即假设同行评价者v的偏见bv服从均值为0且方差为1/η0的高斯分布.
互评分数:互评分数(记为zvi)表示同行评价者v∈V针对被评价者ui提交的主观题作业给出的评价分数.设所有评价者的互评分数集合为Z={zvi|ui∈U,v∈V}.两个概率模型均假设变量zvi服从以高斯分布,且高斯分布的均值等于作业的真实分数si与评价者v的评分偏见bv之和,方差反比于评价者v的可靠性τv.在PG9模型中引入了超参数λ用于调节高斯分布的方差取值.
相对分数:相对分数(记为dvij)表示同行评价者v∈V对被评价者ui∈U和uj∈U的主观题作业给出的互评分数间的差值.记面向所有评价者的相对分数集合为D={dvij|ui,uj∈U,v∈V}.相对分数的引入有利于提高对主观题作业真实分数估计的精度.PG8模型中,相对分数dvij被设定为满足均值为两份被v评价的主观题作业的真实分数之差(即si-sj)、且方差为2/τv的高斯分布.在PG9模型中同样引入了超参数λ用于调节高斯分布的方差取值.
基于以上符号表征,本文的研究问题为:已知所有同行评价者的互评分数集合Z,面向所有评价者的相对分数集合D,所有评价者的知识点掌握程度向量α构成的矩阵M|V|×|KP|,通过构建概率模型PG8和PG9推断出每个同行评价者(即∀v∈V)的可靠性τv、偏见bv以及每个被评价者(即∀ui∈U)提交的主观题作业的真实分数si,可以形式化表示为P({bv|v∈V},{τv|v∈V},{si|ui∈U}Z,D,M).表1总结了模型涉及的主要符号和相关解释.

表1 主要符号及其含义Table 1 Main notations and their descriptions
图1展示了PG8和PG9的概率图模型.可见,同行评价者v针对被评价者ui的主观题作业给出的互评分数zvi、v针对被评价者ui和被评价者uj给出的评价分数之间的相对分数dvij、v的潜在正确作答概率δv是概率图模型中的观测变量.而ui的主观题作业的真实分数si、v的偏见bv、v的可靠性τv则是概率模型估计的隐含变量,且这些隐含变量的先验分布由超参数μ0、γ0、θ1、θ2、η0和β0所确定.由图可知,这些隐含变量彼此间是相联系的.因而,为了估计这些隐含变量的值,基于每个隐含变量的近似后验分布信息,并利用Gibbs采样技术[34]对每个隐含变量的取值进行采样.具体而言,Gibbs采样技术:首先基于每个隐含变量的近似后验分布信息运行若干次Gibbs采样以生成该变量的若干个样本,得到该变量的样本集;其后,当隐含变量样本的分布逐渐趋于收敛和稳定时,基于隐含变量的样本集推断变量的真实值.例如,假定基于Gibbs采样技术所得到的被评价者ui的主观题作业真实分数si的样本集为{s1i,s2i,…,sIGi}且IG为采样的次数,则可基于样本集中样本的平均值来估计si.考虑到Gibbs采样过程存在老化阶段(Burn-in阶段),这时得到的隐含变量的样本不准确,因而基于Gibbs采样技术生成隐含变量的样本集时需要丢弃在老化阶段生成的样本(一般为样本集中的前n个样本).

图1 PG8和PG9的概率图模型Fig.1 Probabilistic graphical model for PG8 and PG9
4.1 PG8模型
PG8模型扩展了现有的PG6模型[9],其的生成过程为:
·对于第i个被评价者ui提交的每份主观题作业
→定义隐含变量si(即ui的真实分数)si~N(μ0,1/γ0)
·对于每个同行评价者v
→定义隐含变量τv(即v的可靠性)τv~Γ(θ1δv+θ2sv,1/η0)
→定义隐含变量bv(即v的偏见)bv~N(0,1/η0)
·对于每个互评分数zvi
→定义可观测变量zvi~N(si+bv,1/τv)
·对于每个相对分数dvij
→定义可观测变量dvij~N(si-sj,2/τv)
由于概率模型PG8中的隐含变量si没有闭式解(close-form solution),因而采用近似离散推断的策略得到该隐含变量的近似后验分布.概率模型PG8中隐含变量的近似后验分布的推断结果如下:
s∝β0θ2siτi(θ2si-1)Γ(θ1δi+θ2si)×exp(R(si-YR)2)
其中R=γ0+∑v∈Vuiτv+∑v∈Vui∑uj∈Uvτv2
(3)
Y=μ0γ0+τv(∑v∈Vui(zvi-bv)+∑v∈Vui∑uj∈Uv(dvij+sj)2)
τ~Γ(θ1δv+θ2sv+|Uv|22,β0+
∑vi∈Uv(zvi-si-bv)2+∑ui,uj∈Uv12(dvij-si+sj)2)
(4)
b~N∑ui∈Uvτv(zvi-si)η0+|Uv|τv,1η0+|Uv|τv
(5)
4.2 PG9模型
PG8模型与PG9模型的区别在于PG8模型假同行设评价者的可靠性满足伽马分布而PG9模型则假设同行设评价者的可靠性满足高斯分布.PG9模型扩展了现有的PG7模型[9],其的生成过程为:
· 对于第i个被评价者ui提交的每份主观题作业
→定义隐含变量si(即ui的真实分数)si~N(μ0,1/γ0)
· 对于每个同行评价者v
→定义隐含变量τv(即v的可靠性)τv~N(θ1δv+θ2sv,1/η0)
→定义隐含变量bv(即v的偏见)bv~N(0,1/η0)
· 对于每个互评分数zvi
→定义可观测变量zvi~N(si+bv,λ/τv)
· 对于每个相对分数dvij
→定义可观测变量dvij~N(si-sj,2λ/τv)
由于PG9模型中的隐含变量si和τv没有闭式解,因而采用近似离散推断的策略得到该隐含变量的近似后验分布.概率模型PG9中隐含变量的近似后验分布的推断结果如下:
s∝β0θ2siτi(θ2si-1)Γ(θ1δi+θ2si)×exp(R(si-YR)2)
其中R=γ0+∑v∈Vuiτvλ+∑v∈Vuiτv*(|Uv|-1)2λ
(6)
Y=γ0μ0+τvλ∑v∈Vui(zvi-bv)+∑v∈Vui∑uj∈Uv(dvij+sj)2
τ∝τv|Uv|22×exp-β02τv-θ1δv+θ2sv+
∑ui∈Uv(zvi-si-bv)2λβ0+∑ui,uj∈Uv(dvij-si+sj)22λβ02
(7)
b~N∑ui∈Uvτvλ(zvi-si)η0+|Uv|τvλ,1η0+|Uv|τvλ
(8)
4.3 真实分数估计步骤
利用PG8模型和PG9模型即可估计一份主观题作业的真实分数,具体分为以下4个步骤:
步骤1.认知诊断.以所有同行评价者的历史答题记录为输入,利用DINA 模型诊断得到记录了他们对所有知识点的掌握程度信息的矩阵M.
步骤2.推理.由于概率模型中的各个变量是相互联系的,因而基于模型中观测变量的观测值(包括同行评价者v的潜在正确作答概率(v、互评分数zvi和相对分数dvij)推断模型中隐含变量(包括同行评价者的偏见bv、可靠性τv和被评价者ui的主观题作业的真实分数si)的后验概率分布是一个循环推理的过程,最终推理得到PG8模型中各个隐含变量的近似后验分布(循环推理得到的近似后验概率分布如公式(3)-公式(5)所示)以及PG9模型中各个隐含变量的近似后验分布(循环推理得到的近似后验概率分布如公式(6)-公式(8)所示).
步骤3.采样.以互评分数集合、相对分数集合和步骤一得到的知识点的掌握程度矩阵M为输入,以Gibbs采样技术为采样框架并利用步骤2得到的各个隐含变量的近似后验分布得到概率模型中每个隐含变量的多个样本值.
步骤4.整合.对步骤3得到的概率模型中的每个隐含变量的多个样本值进行整合,进而得到每个隐含变量(包括主观题作业的真实分数)的估计值.
5 实 验
基于真实采集的主观题同行互评数据集,本节对本文提出的基于认知诊断的主观题同行互评技术PG8、PG9和相关的主观题同行互评技术进行了实验比较.
5.1 数据集
为了验证本文提出的基于认知诊断的同行互评技术对于主观题评判的有效性,基于自主研发的“会了吗”在线教学服务系统[37]收集计算机专业核心主干课“数据库原理”中“关系数据库规范化理论”这一节的真实教学数据,得到涉及关系数据库规范化理论相关知识点的主观题同行互评数据集以及客观题测试结果数据集.
5.1.1 主观题同行互评数据集
在“会了吗”在线教学服务系统中实现了主观题作业的互评功能.通过给“数据库原理”课程的5个本科平行教学班的284名学生布置考察了关系数据库规范化理论的3次主观题作业并组织他们进行同行互评从而得到主观题同行互评数据集.每次主观题作业仅包含一道主观题,且布置的3次主观题作业涉及考察关系数据库规范化理论的11个知识点,这些知识点和它们的编号分别为:1)一范式;2)二范式;3)三范式;4)BC范式;5)主属性;6)传递函数依赖;7)决定因素;8)函数依赖;9)码;10)部分函数依赖;11)非主属性.这些知识点是数据库原理这门课的教学难点,而主观题形式的作业比客观题形式的作业能更好地帮助学生巩固对这些知识点的学习.图2给出了记录了3次主观题作业所考察知识点信息的Q矩阵.

图2 主观题作业的Q矩阵Fig.2 Q matrix of subjective questions
在主观题作业的互评教学活动中,每名学生既是提交主观题作业的提交者(即被评价者)又是评判同行提交的主观题作业的评价者.每个评价者都会收到系统随机给其派发的3份主观题作业,并要求其遵循教师制定的评分指导规则完成对这3份主观题作业的判分.需要说明的是,为了保证互评的质量,互评活动采用双盲的方式进行.为了评估不同主观题互评技术对于主观题作业真实估计的准确性,邀请拥有6年以上“数据库原理”课程教学经验的教师对每份学生提交的主观题作业进行评价打分,并以教师的评分作为该主观题作业的真实分数.表2给出了从3次主观题作业的互评教学活动收集到的主观题同行互评数据集的相关统计信息.
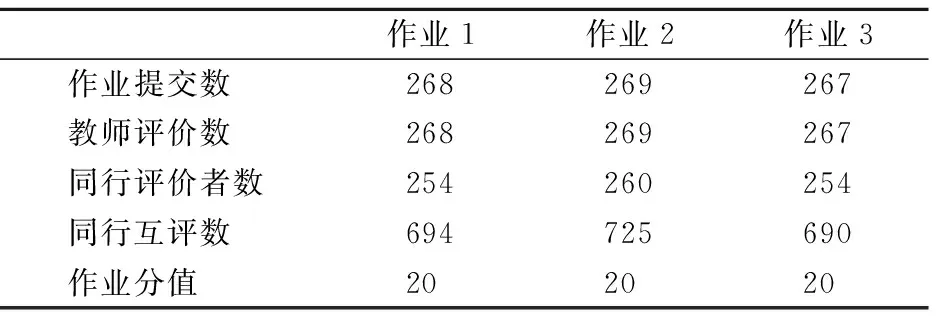
表2 主观题同行互评数据集的统计信息Table 2 Statistics of our subjective question dataset for peer grading
5.1.2 历史客观题测试结果数据集
为了能够基于DINA模型诊断学生对主观题的掌握程度,要求学生们在“会了吗”在线教学服务系统上完成包含40道客观题的在线测试.这些客观题覆盖了3次主观题作业考察的关系数据库规范化理论的11个知识点.基于在线测试活动得到的每名学生的客观题测试结果数据和记录了每道客观题考察的知识点信息的Q矩阵(如图3所示),从而可基于DINA模型诊断每名学生对11个知识点的掌握程度,进而可计算每名学生对每道客观题作业的掌握程度.
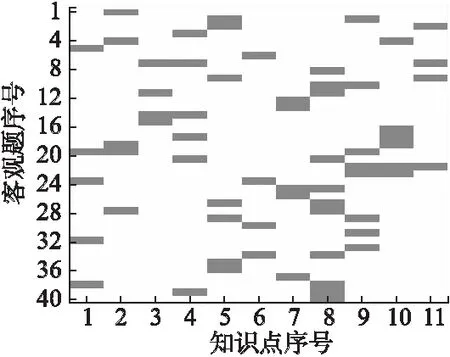
图3 每道客观题考察的知识点信息的Q矩阵Fig.3 Q matrix of objective questions
5.2 参与比较的主观题同行互评技术
为了评估本文提出的PG8模型与PG9模型的有效性,将它们与其它主观题同行互评技术进行比较,具体包括:
·中位数:即用一份主观题作业所获得的所有评价分数的中位数估计该作业的真实分数,这也是当今大多数提供主观题互评功能的MOOC平台(例如Coursera和中国大学MOOC)采用的估计主观题作业真实分数的方法.
·均值:即用一份主观题作业所获得的所有评价分数的均值估计该作业的真实分数.
·PG6和PG7[9]:PG6和PG7均是解决主观题同行互评问题的现有最先进概率模型.本文提出的PG8与PG9模型分别是在PG6和PG7模型的基础上对评价者可靠性进行了建模优化.具体而言,PG6和PG7模型在评价者可靠性时仅考虑了其在当前主观题作业中的答题表现,而PG8与PG9模型在对评价者的可靠性进行建模时不但考虑了其在当前作业中的答题表现还考虑了基于其历史答题表现诊断得到的评价者对待评价作业的掌握程度信息,以期提高概率模型对主观题作业真实分数估计的精确性.需要说明的是:1)PG8与PG6相对应,均假设同行评价者互评可靠性取值的先验分布为伽马分布;2)PG9与PG7相对应,均假设同行评价者互评可靠性取值的先验分布为高斯分布.
5.3 实验设置
本文提出的主观题同行互评技术和相关主观题同行互评技术PG6和PG7均是利用概率模型对同行评价者的互评可靠性和互评偏见进行建模,因而都使用了一些超参数.为这些超参数设置合理的值对准确估计主观题作业的真实分数非常重要.对于概率模型中的真实分数变量si服从的高斯分布的超参数,即均值μ0和方差1/γ0,分别设置为所有主观题作业互评分数的均值和方差.根据文献[7,9]的参数设置,本文的具体调整策略为:对于PG8和PG6,在其它参数取值固定的前提下,以50为步长尝试超参数β0在[150,400]范围中的不同取值,然后以该技术所得到的对真实分数最准确的估计值为该技术的最终估计值;对于PG9和PG7,在其它参数取值固定的前提下,以0.2为步长尝试超参数λ在[0.6,1.6]范围中不同取值,然后以该技术所得到的对真实分数最准确的估计值为该技术的最终估计值.由于基于概率模型的同行互评技术在估计主观题作业真实分数时具有一定的随机性,因此对于超参数集合的每种设定,每种技术都执行10次真实分数的推断算法.对于基于概率模型的同行互评技术中每个需要估计的隐含变量,推断算法均迭代运行600次Gibbs采样获取隐含变量的样本值,并设定前60次采样得到的样本为老化阶段的样本,这些老化阶段的样本将不参与对真实分数的估计运算.
所有参与比较的主观题同行互评技术均基于Python(v3.7)语言实现,并在配备了i5-8500 3GHZ CPU、8GB内存、1TB硬盘,运行了64位Windows 10操作系统的服务器上进行统一实验测试.
5.4 实验结果
5.4.1 同行互评技术的估计准确性
采用不同技术给出的对主观题真实分数的估计值和主观题作业真实分数之间的均方根误差(即RMSE)作为不同同行互评技术有效性的评估指标.RMSE被广泛应用于评估同行互评技术有效性[6,8].表3展示了不同主观题同行互评技术估计主观题作业真实分数的准确性.需要说明的是,表中的RMSE表示互评技术10次迭代得到的RMSE的平均值,而STD表示RMSE的标准差.由表3可知,本文提出的基于认知诊断的同行互评技术PG8和PG9在3份主观题作业中的估计准确率均高于比其他技术.由于同时考虑了同行评价者在本次作业中的答题表现以及评价者的历史答题表现对其评分可靠性的影响,PG8和PG9技术对3次作业真实分数的平均估计误差比PG6和PG7技术平均降低了42%.实验结果证实了结合本次作业中的答题表现以及评价者的历史答题表现建模可靠性对于基数同行互评估计的有效性.

表3 估计真实分数的准确性Table 3 Error of true score estimation
5.4.2 同行互评技术的最大估计误差
通过衡量主观题作业真实分数估计值与教师批改分数之间的最大评分偏差来分析同行互评技术的评估表现,如表4所示.从表中可看出,均值技术与中位数技术的最大评分偏差是最大的,而基于认知诊断的同行互评技术PG8和PG9在3份主观题作业中的最大评分偏差是最小的,说明同行评价者对主观题作业考察的知识点的掌握程度信息使概率模型能更有效地保障对每个学生的主观题作业真实分数的估计准确性.同时还可观察到,PG8和PG9技术对3次作业真实分数估计的最大评分误差均低于PG6和PG7技术,进一步表明了同时考虑影响可靠性的两方面因素(即同行评价者在本次作业中的答题表现以及评价者的历史答题表现)能够提升对主观题作业真实分数估计的精确性.
5.4.3 同行互评技术的超参数敏感性

表4 真实分数估计值与真实分数间的最大评分偏差Table 4 Maximum deviation between an estimated grade and ground truth for all students
为了表明PG8技术中的超参数β0和PG9技术中的超参数λ对主观题作业真实分数估计的影响,本文采取固定其他超参数值的策略并对这两个超参数的值进行了实验分析.在实验中为了测试模型的敏感性,将PG8中的超参数β0设置在[150,400]范围内以50为步长变化,实验结果如图4;将PG9中的超参数λ设置在[0.6,1.6]范围内以0.2为步长变化,实验结果如图5所示.图4和图5的结果表明:在合理的取值范围内,这两种技术对超参数值具有鲁棒性,它们对主观题作业真实分数的估计误差都控制在可接受的范围.
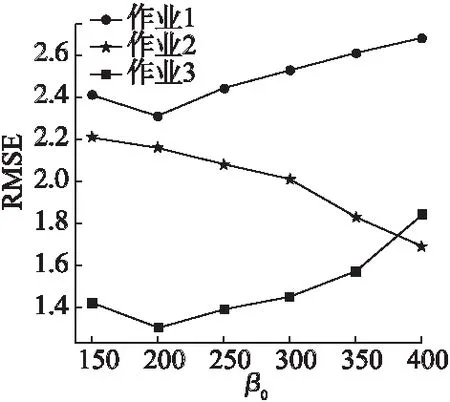
图4 PG8技术的超参数敏感性分析Fig.4 Sensitivity analysis of hyper-parameter for PG8

图5 PG9技术的超参数敏感性分析Fig.5 Sensitivity analysis of hyper-parameter for PG9
6 总 结
同行互评是当前大型开放式网络课程(MOOCs)平台用以解决大规模主观题作业评价的主流方式.同行评价者的评分偏见和评分可靠性是未知的,因此基于多个同行评价者给出的评价分数估计主观题作业的真实分数是一个具有挑战的问题.现有同行互评技术利用概率模型对同行评价者的评分可靠性和评分偏见进行建模,有效提高了估计主观题作业的真实分数的准确性.然而,这些技术均未同时考虑同行评价者在本次作业中的答题表现以及评价者的历史答题表现对其评分可靠性的影响.鉴于此,本文在现有概率模型的基础上提出了基于认知诊断的主观题同行互评技术,包含PG8和PG9两个概率模型.PG8和PG9利用教育评估领域流行的认知诊断DINA模型诊断得到同行评价者对主观题的掌握程度信息并结合评价者在待评价作业中的答题表现对评价者评分可靠性进行建模,实验证实PG8和PG9比相关最好的同行技术在提升主观题作业真实分数估计准确性方面更有优势.

