钢筋钢丝网砂浆加固钢筋混凝土方柱耗能特性数值分析

吴小勇， 熊琦龙， 周凯

(1.防灾减灾湖北省重点实验室， 宜昌 443002； 2.三峡大学土木与建筑学院， 宜昌 443002)

由于地震突发性与破坏性的特点，给世界各国带来巨大的人员伤亡和经济损失[1]。钢筋混凝土柱是框架结构承受水平和竖向荷载的重要构件，其抗震性能直接关系到震害中建筑结构的安全性能。历次震害表明，震害大多发生于柱端(呈强梁弱柱)和节点[2-3]。在强震作用下钢筋混凝土柱地震损伤产生非线性残余变形，同时结构的使用功能与安全强度储备能力部分丧失[4]。为了保证建筑结构的安全性，对钢筋混凝土柱的抗震加固展开研究具有重要的理论意义和工程价值。

目前，对钢筋混凝土柱的抗震性能研究主要有试验研究和数值分析两种方式[5-7]。张玉等[8]对高性能水泥复合砂浆钢筋网薄层 (high performance ferrocement laminate, HPFL)加固钢筋混凝土(reinforced concrete, RC)柱的配箍率、配筋率、混凝土强度和钢绞线进行参数分析，结果表明，随着各参数增加加固柱的极限承载力和延性均得到不同程度的提高。Jauhari等[9]对纤维混凝土板加固型钢混凝土柱的抗震性能进行研究，对纤维混凝土板的抗拉强度进行了参数化分析，结果显示，纤维混凝土板的抗拉强度从8 MPa增加到16 MPa，其耗能能力增加5%～17%。张童等[10]和尹世平等[11]分析了不同参数对纤维编织网增强混凝土加固RC柱抗震性能的影响，结果表明，随着配箍率增加或轴压比减小，加固RC柱的延性系数和耗能能力不断提高。Wang等[12]研究了轴压比、剪跨比、钢管厚度、纵向配筋率、玻璃纤维增强复合材料(glass fiber reinforced polymer, GFRP)布层数5种因素对玻璃纤维增强聚合物和钢管加固混凝土柱抗震性能的影响，结果表明，轴压比、剪跨比、钢管厚度和纵向配筋率增加，加固柱的承载力提高，但轴压比和剪跨比增加时延性明显降低；周长东等[13]研究了轴压比对碳纤维布预应力加固混凝土柱滞回性能的影响，结果表明，预应力碳纤维布加固混凝土柱能显著提高柱的耗能性能，随着轴压比的减小加固柱的耗能能力明显增强。司建辉等[14]利用ABAQUS建立了绕丝加固柱的数值模型，分析了轴压比和钢丝绳环绕方式对加固柱抗震性能的影响，结果表明，轴压比的提高使加固柱的承载力增加显著，但延性性能降低。可见，不同参数对加固RC柱的抗震性能有着显著影响，而地震作用实质是能量的传输与消耗，因此加固RC柱的耗能特性有待进一步研究。

钢筋钢丝网砂浆加固凭借钢丝网优越的配筋分散性可使砂浆层保持裂而不碎，显著增加结构的耗能，同时采用大直径的钢筋网能够显著提高结构的承载力，但是进行大量抗震试验是不切实际的。为此，在试验研究[3]基础上，结合钢筋钢丝网砂浆加固柱的约束效应，建立了钢筋钢丝网约束混凝土的应力-应变关系，通过数值方法更多的分析钢筋钢丝网砂浆加固柱的抗震特性，以弥补有限试验量的不足；同时对影响钢筋钢丝网砂浆加固柱耗能特性的剪跨比、纵筋配筋率、配箍率、混凝土强度等级和轴压比等参数进行分析。

1 材料特性及试件分组

选取文献[3]中3根试验柱，分别为未加固试件、钢筋网加固试件和钢筋加一层钢丝网加固试件，分别记为O、S和FS。混凝土配合比为水∶水泥∶砂∶石头=0.44∶1∶1.5∶2.41，实测28 d立方体抗压强度为43.2 MPa；外抹砂浆配合比为水∶水泥∶砂=0.44∶1∶2，实测28 d立方体抗压强度为36.6 MPa。轴压比为0.33，其他参数如图1所示。

箍筋直径为6 mm，屈服强度和极限强度分别为403.2 MPa和502.7 MPa，纵向钢筋直径为10 mm和12 mm，屈服强度和极限强度分别为370.3 MPa和638.8 MPa，镀锌焊接钢丝网直径为1.2 mm，屈服强度和极限强度分别为350.1 MPa和399.4 MPa。钢丝网网格间距为11 mm×11 mm，试验中各构件的主要参数如表1所示。

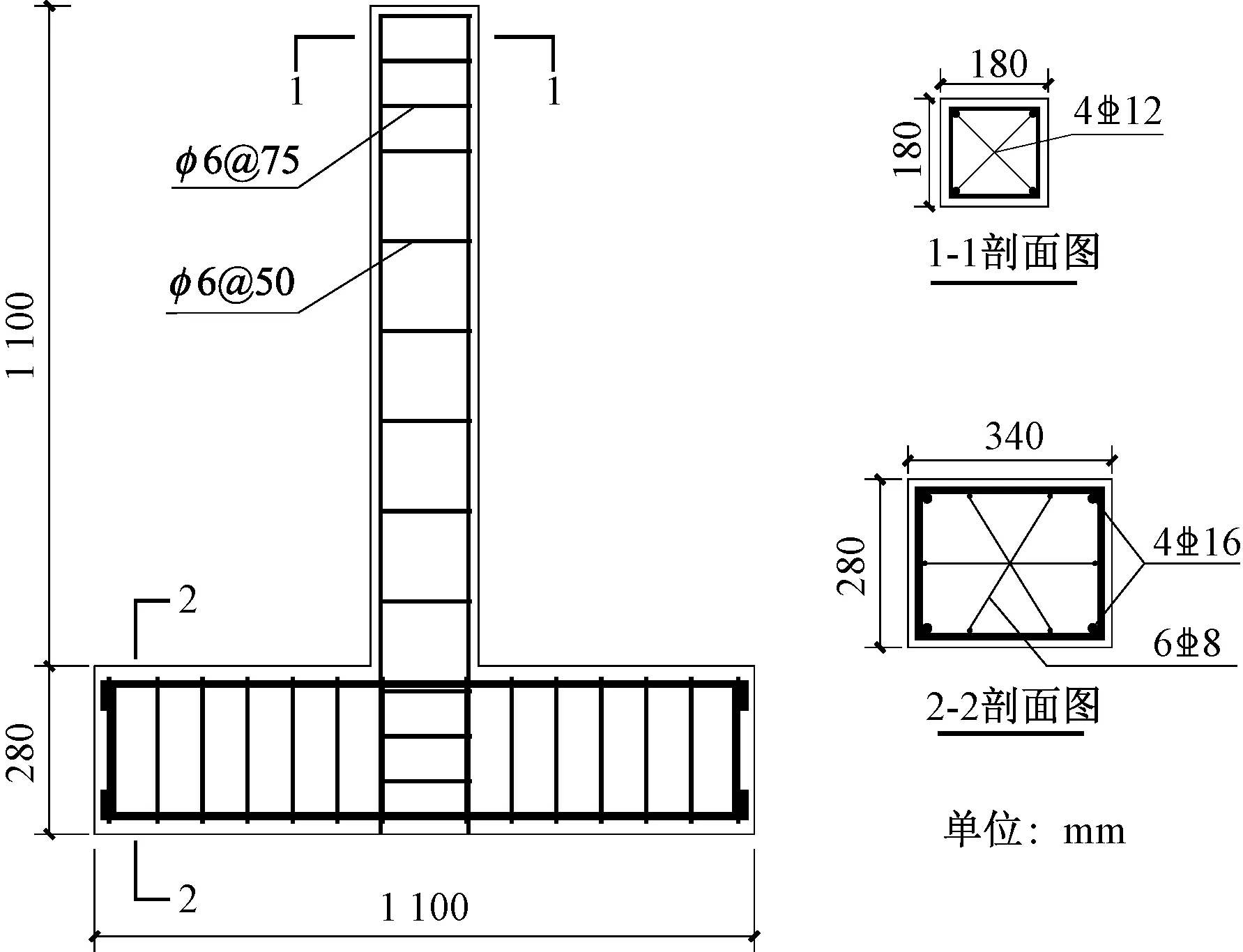
图1 钢筋混凝土柱试件尺寸及配筋图Fig.1 Size and reinforcement of RC columns

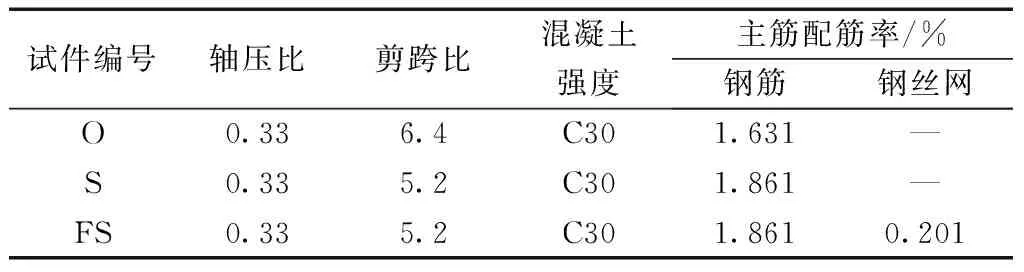
表1 试件参数Table 1 Main parameters of specimens

2 模型建立与验证

2.1 单元选取

混凝土、砂浆和加载板采用C3D8R单元，该单元能兼顾模型精确性和求解效率，钢筋骨架、钢筋网和钢丝网采用T3D2单元。

2.2 混凝土本构模型

2.2.1 钢筋钢丝网对混凝土的约束效应

轴向荷载作用下，钢筋钢丝网加固的混凝土方柱会发生横向膨胀，钢筋网和钢丝网会约束混凝土的横向膨胀变形。钢筋网和钢丝网受到环向拉应力，对混凝土方柱产生环向压应力，因而提高混凝土的强度。参考Sheikh等[15]研究方法将混凝土方柱的截面分为强约束区和弱约束区，强弱约束区交界处为4条标准二次抛物线，抛物线与柱边夹角是45°，如图2所示。

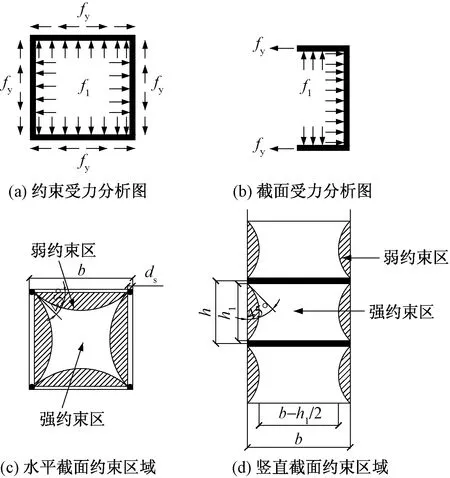
fy为钢筋网(或钢丝网)的屈服强度； f1为钢筋网(或钢丝网)对混凝土方柱的侧向约束应力； h1为钢筋网箍筋(或钢丝网网格)净距; b为混凝土柱的边长；ds为钢筋网纵向钢筋直径；图2 钢筋混凝土柱约束区域及受力分析Fig.2 Confined area and stress analysis of RC columns

考虑混凝土方柱存在弱约束区域，侧向约束应力不能充分发挥效应，引入有效约束系数Ke(混凝土方柱强约束区面积与包围混凝土方柱面积之比)来计算钢筋网和钢丝网对混凝土方柱的有效侧向约束应力。当钢筋钢丝网加固的混凝土方柱达到极限强度时，认为钢丝网的应力和钢筋网箍筋的应力均达到屈服强度，由图2所示，钢筋网和钢丝网对混凝土方柱的侧向约束应力可以由截面受力平衡得到。

(1)

(2)

式中：fls为钢筋网对混凝土方柱的侧向约束应力；flw为钢丝网对混凝土方柱的侧向约束应力；Afs为钢筋网箍筋的截面面积；Afw为钢丝网的截面面积；fys为钢筋网箍筋的屈服强度；fyw为钢丝网的屈服强度；hs为钢筋网箍筋的间距；hw为钢丝网网格间距；n为钢丝网层数。

f′ls=Kesfls

(3)

f′lw=Kewflw

(4)

(5)

(6)

(7)

Acs=b2(1-ρs)

(8)

(9)

Acw=b2

(10)

式中：f′ls为钢筋网对混凝土方柱的有效侧向约束应力；f′lw为钢丝网对混凝土方柱的有效侧向约束应力；Kes为钢筋网有效约束系数；Kew为钢丝网有效约束系数；Aes为钢筋网加固混凝土方柱强约束区域面积；Acs为钢筋网包围混凝土方柱面积；Aew为钢丝网加固混凝土方柱强约束区域面积；Acw为钢丝网包围混凝土方柱面积(混凝土方柱横截面面积)；h1s为钢筋网箍筋净间距；h1w为钢丝网网格净间距；ρs为钢筋网纵向钢筋配筋率。

钢筋钢丝网对混凝土方柱的有效侧向约束应力可用钢筋网对混凝土方柱的有效侧向约束应力、钢丝网对混凝土方柱的有效侧向约束应力以及钢筋骨架对核心混凝土区域的有效侧向约束应力之和表示，计算公式为

f′lsw=f′ls+f′lw+f′lo

(11)

式(11)中：f′lsw为钢筋钢丝网对混凝土方柱的有效侧向约束应力；f′lo为钢筋骨架对核心混凝土区域的有效侧向约束应力，计算公式参见文献[16]。

2.2.2 混凝土本构关系

根据有效侧向约束应力与混凝土强度提高系数的关系，在Mander约束混凝土应力-应变模型基础上[14]，建立钢筋钢丝网约束混凝土的应力-应变关系，其表达式为

(12)

fcc=Kcfco

(13)

(14)

(15)

εcc=εco[1+5(Kc-1)]

(16)

式中：fc为混凝土纵向压应力；ε为混凝土纵向应变；fcc为约束混凝土峰值抗压强度；fco为未约束混凝土立方体抗压强度；Kc为混凝土强度提高系数；εcc为约束混凝土抗压强度对应的峰值应变；εco为未约束混凝土立方体抗压强度对应的峰值应变；r为约束混凝土应力-应变曲线系数；Ec为未约束混凝土弹性模量，取值为Ec=4 730。

混凝土受拉应力-应变关系采用双折线模型，混凝土应变达到峰值拉应变之前为弹性上升段；在峰值拉应变之后为线性受拉下降段；当混凝土应变达到极限拉应变，混凝土抗拉强度下降到0，混凝土峰值拉应变取值为0.001。

2.3 钢筋、钢丝网及砂浆本构模型

参考文献[17]子程序钢筋本构关系，该模型能考虑钢筋与混凝土的粘结滑移效应，通过定义滞回耗能系数和体现重加载段刚度先弱后强的特征来模拟这种效果[17]。

钢丝网的材料参数采用ABAQUS中弹塑性材料模型来定义，由于钢丝网不是线弹性材料，选用实测的钢丝网应力-应变曲线进行输入[2]。

考虑砂浆的力学性能与混凝土材料的力学性能相似，本文采用同强度的混凝土本构关系来表达砂浆的本构关系，砂浆应力-应变关系参考《混凝土结构设计规范》(GB 50010—2010)推荐的混凝土单轴拉压应力-应变关系模型。砂浆的材料参数同样采用混凝土塑性损伤模型来定义。

3 有限元模型验证

3.1 破坏形态

从图3可以看出，在峰值位移处，O柱底侧面边缘处产生的塑性应变较大，沿竖向分布，柱侧出现裂缝并沿竖向延伸；在破坏位移处，柱两侧竖向塑性应变和柱底上方横向塑性应变均变大，柱两侧竖向裂缝变宽，裂缝数量变多并出现横向贯通的趋势，与O柱试验的破坏形态图相吻合。

图3 O试件最大主塑性应变云图与试验破坏形态Fig.3 Diagram of maximum principal plastic strain and experimental failure patterns of O test-piece

从图4可以看出，在峰值位移处，S柱底侧的塑性应变较大，出现斜向发展的塑性应变区域，说明沿柱侧出现弯剪斜向裂缝，在破坏位移处，柱底塑性铰区域两侧出现了较大的破坏应变，与S柱试验的破坏形态图相吻合。

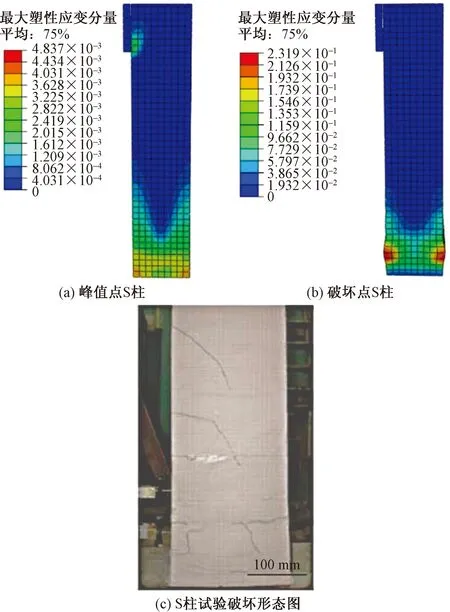
图4 S试件最大主塑性应变云图与试验破坏形态图Fig.4 Diagram of maximum principal plastic strain and experimental failure patterns of S

从图5可以看出，在峰值位移处，FS柱最大主塑性应变分布区域较广，这主要得益于钢丝网优越的配筋分散性；在破坏位移处，塑性应变主要集中在柱底区域，此处砂浆已达到破坏应变，与FS柱砂浆剥落现象相吻合。

图5 FS试件的最大主塑性应变云图与试验破坏形态图Fig.5 Diagram of maximum principal plastic strain and experimental failure patterns of FS

3.2 滞回性能

从图6可以看出，滞回曲线模拟结果与试验结果吻合较好，数值计算的滞回曲线正反方向形状基本对称。模拟的峰值荷载值要略高于试验的峰值荷载值，O试件数值计算的峰值荷载为40.01 kN，试验峰值荷载为33.11 kN，数值模拟结果较试验结果高了20.8%；S试件数值计算的峰值荷载为46.3 kN，试验峰值荷载为35.29 kN，数值模拟结果比试验结果高了31.2%；FS试件数值计算的峰值荷载为48.82 kN，试验峰值荷载为41.26 kN，数值模拟结果比试验结果高了18.3%。数值模拟和试验之间存在一定的误差，考虑到试件制作过程中不可避免存在的初始缺陷，模拟初始刚度相对试验过高。不过从结果来看，数值模拟采用的本构关系和分析参数能够较好地模拟出加固柱的受力状态，建立模型较为合理。

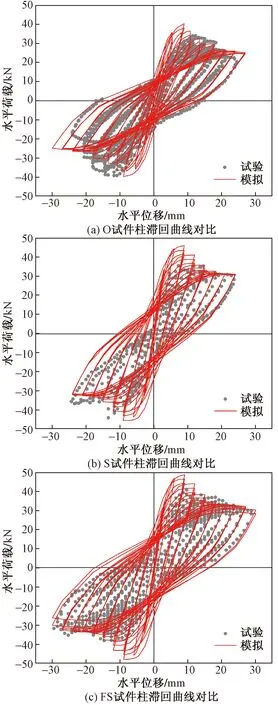
图6 数值模拟滞回曲线与试验结果对比Fig.6 Comparison between numerical simulation hysteresis curve and experimental results

3.3 骨架曲线

骨架曲线是每级循环荷载下最大侧向荷载点连线，反映了构件在不同阶段所受荷载与变形之间的关系，同时也能体现构件的耗能、刚度、延性和抗倒塌的能力。图7为数值模拟骨架曲线计算结果与试验骨架曲线的对比结果，在初始加载阶段数值模拟与试验结果具有很好的吻合性，随着加载的进行，数值计算的曲线要高于试验曲线，在达到极限荷载后，数值计算的曲线刚度退化比试验曲线要快，产生这一现象的原因是在进行ABAQUS软件分析时认为裂缝垂直方向上混凝土刚度为0，而实际中混凝土开裂会产生微裂缝，由于混凝土内部粗细骨料之间有粘聚咬合作用，实际中的混凝土截面刚度退化不会直接下降到0。

4 参数分析

由于钢筋钢丝网加固柱相关试验研究有限，为进一步探究剪跨比、纵筋配筋率、配箍率、混凝土强度等级和轴压比对钢筋钢丝网砂浆加固柱耗能特性的影响，利用ABAQUS数值软件共设计了72个钢筋钢丝网砂浆加固柱模型试件。加固柱的柱长统一设计为1 100 mm，加固前的方柱截面统一设计为180 mm×180 mm，保护层厚度为20 mm，加固后的方柱截面统一设计为230 mm×230 mm。

4.1 剪跨比的影响

考虑剪跨比5.2、4.2、3.3和2.4这4个水平，将混凝土强度等级和轴压比保持不变，分别取值为39.47 MPa和0.33，共设计了16个试件，记为K1～K16，如表2所示。在纵筋配筋率为1.861%～2.587%和配箍率为0.43%～0.61%时，随着剪跨比的减小，低纵筋配筋率和高配箍率对试件极限荷载增幅提高了20.26%～49.82%，低纵筋配筋率和低配箍率对试件耗能能力的增幅提高了0.8～1.1倍，其中剪跨比为4.2的试件归一化总滞回耗能都较大，其耗能能力在剪跨比5.2、4.2、3.3和2.2这4个水平下表现最好。

图7 数值模拟骨架曲线与试验结果对比Fig.7 Comparison between numerical simulation skeleton curve and experimental results

4.2 纵筋配筋率的影响

考虑纵筋配筋率0.967%、1.861%、2.587%和3.410%这4个水平，将剪跨比和轴压比保持不变，分别取值为5.2和0.33，共设计了16个试件，记为L1～L16，如表2所示。在配箍率为0.43%～0.61%和混凝土强度等级为39.47～52.63 MPa时，随着纵筋配筋率的增加，低混凝土强度等级和低配箍率对试件极限荷载增幅提高了38.40%～104.91%，高配箍率和高混凝土强度等级对试件的耗能能力增幅提升了31.21%～56.33%。

4.3 配箍率的影响

考虑配箍率0.43%、0.61%和0.78%这3个水平，将纵筋配筋率和剪跨比保持不变，分别取值为2.587%和5.2，共设计了12个试件，记为M1～M12，如表3所示。在混凝土强度等级为39.47～52.63 MPa和轴压比为0.33～0.6时，各试件的极限荷载随配箍率的增加变化并不明显；随着配箍率的增加，低混凝土强度等级试件的耗能能力提升了21.15%～44.77%，高混凝土强度等级试件的耗能能力变化并不明显，低轴压比试件的耗能能力增幅比高轴压比试件提升了7.03倍。

4.4 混凝土强度等级的影响

考虑混凝土强度等级39.47、52.63、65.79 MPa这3个水平，将配箍率和剪跨比保持不变，分别取值为0.43%和5.2，共设计了12个试件，记为N1～N12，如表3所示。在纵筋配筋率为1.861%～2.587%和轴压比为0.33～0.6时，随着混凝土强度等级的增加，低纵筋配筋率和高轴压对试件极限荷载增幅提高了39.24%～74.85%，低纵筋配筋率试件的耗能能力增幅比高纵筋配筋率试件提高了93.31%；低轴压比试件随着混凝土强度等级的增加耗能能力提升了36.67%，高轴压试件随着混凝土强度等级的增加耗能能力变化并不明显；试件混凝土强度等级52.63 MPa的归一化总滞回耗能都较大，其耗能能力在混凝土强度等级3个水平下表现最好。

表2 剪跨比、纵筋配筋率试件极限荷载及归一化总滞回耗能Table 2 Ultimate load and normalized total hysteretic energy dissipation of specimens with shear span ratio and longitudinal reinforcement ratio

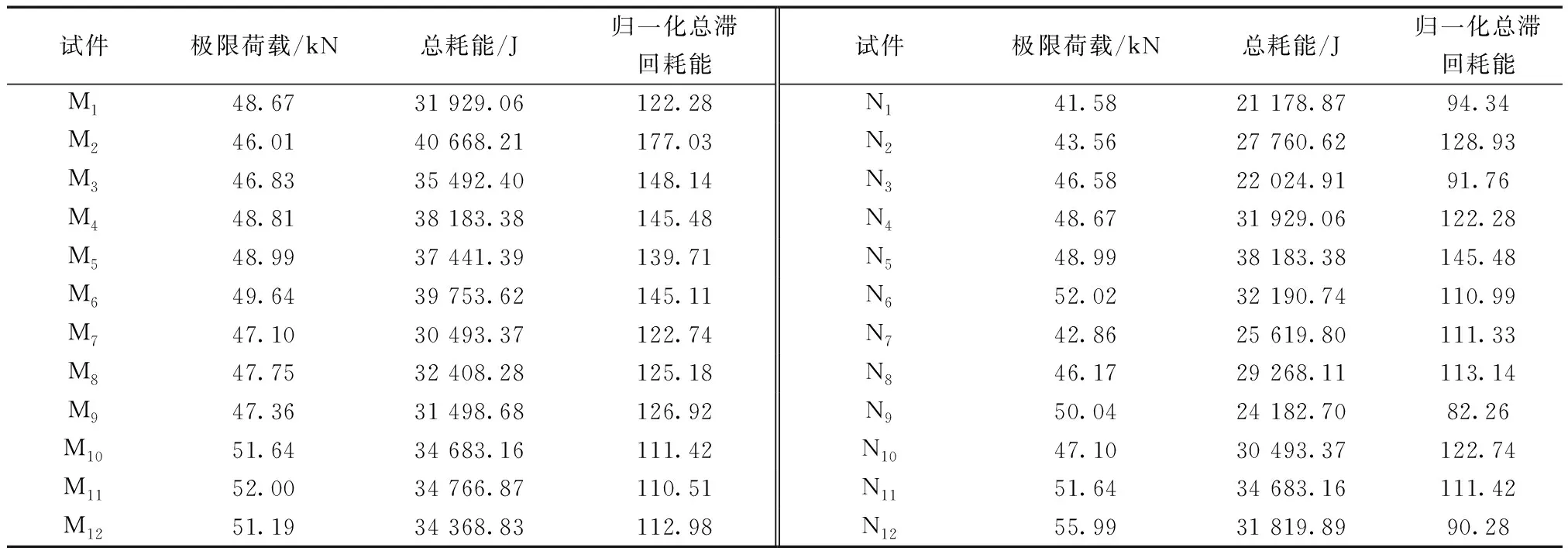
表3 配箍率、混凝土强度等级试件极限荷载及归一化总滞回耗能Table 3 Ultimate load and normalized total hysteretic energy consumption of specimens with stirrup ratio and concrete strength grade

4.5 轴压比的影响

考虑轴压比0.2、0.33、0.6和0.8这4个水平，将配箍率和混凝土强度等级保持不变，分别取值为0.43%和39.47 MPa，共设计了16个试件，记为P1～P16(表4)。在剪跨比为4.2～5.2和纵筋配筋率为1.861%～2.587%时，随着轴压比的增加，低剪跨比和低纵筋配筋率对试件极限荷载增幅提高了39.60%～72.35%；随着轴压比的减小，低剪跨比试件的耗能能力增幅比高剪 跨比试件提高了2.97倍，低纵筋配筋率试件的耗能能力增幅比高纵筋配筋率试件提高了0.48%～30.84%；轴压比为0.2试件的归一化总滞回耗能都较大，其耗能能力在轴压比四个水平下表现突出。

4.6 各因素灰色关联度分析

运用灰色系统理论，进行了不同轴压比(0.2、0.33、0.4、0.6、0.7、0.8和0.9)、不同剪跨比(2.4、3.3、4.2和5.2)、不同混凝土强度(39.5、52.6、59.2、65.8、79.0 MPa)、不同纵筋配筋率(0.967%、1.861%、20587%、3.410%和4.334%)和不同配箍率(0.43%、0.61%和0.78%)的灰色关联分析，得到了各因素对加固柱耗能能力影响程度的子因素序列关联度分别为0.67、0.80、 0.74、 0.78和0.76，表明五种因素对钢筋钢丝网砂浆加固柱耗能能力的影响程度从大到小依次为：剪跨比、纵筋配筋率、箍筋间距、混凝土强度和轴压比。

5 结论

根据钢筋钢丝网砂浆对混凝土的约束机制，基于Mander模型建立了钢筋钢丝网约束混凝土的应力-应变关系，进而构建合理的数值模型。同时，通过ABAQUS数值软件对钢筋钢丝网砂浆加固柱耗能特性进行了参数分析。得出以下主要结论。

(1)所建立的数值模型能够较好地模拟钢筋钢丝网砂浆加固RC柱在低周往复加载下的受压破碎、受拉开裂和刚度退化等情况，与试验的结果吻合较好，所建立的模型具有一定的可靠性。

表4 轴压比试件极限荷载及归一化总滞回耗能Table 4 Ultimate load and normalized total hysteretic energy consumption of specimens with an axial compression ratio

(2)数值模型参数分析结果表明：在本文给定参数范围内，剪跨比从4.2降到2.4，各试件的耗能能力依次降低；纵筋配筋率从0.967%增加到2.587%，各试件的耗能能力依次增加；配箍率从0.43%增加到0.61%，低混凝土强度和低轴压比试件耗能能力提升幅度最大，高轴压比试件的耗能能力变化不明显；混凝土强度等级从52.63 MPa增加到65.79 MPa，各试件耗能能力整体上呈降低趋势；轴压比从0.2增加到0.33，各试件耗能能力依次降低。

(3)综合分析，影响试件耗能大小因素依次为剪跨比、纵筋配筋率、配箍率、混凝土强度等级和轴压比。