基于不规则颗粒的砾岩力学性能数值模拟研究

李皋， 舒淋， 简旭， 李泽， 王智辉

(1.西南石油大学油气藏地质及开发工程国家重点实验室， 成都 610500； 2.中国石油集团川庆钻探工程有限公司川东钻探公司， 重庆 401147)

砾岩是指由30%以上直径大于2 mm的颗粒碎屑组成的岩石，由于颗粒和胶结物的相互作用，砾岩的强度和变形十分复杂。在砾岩油藏的开采过程中，经常发生由于井周失稳引起的坍塌、径缩、卡钻等一系列井下复杂情况[1]。因此，有必要针对砾岩的力学性质开展专门的研究。

张重阳等[2]对KS地区砾岩开展了力学实验，表明砾石层岩石力学参数变化范围大、离散性强，其强度受到砾石颗粒和胶结物基质共同的影响。李振嵩等[3]对第三系砾岩胶结物成分进行了分析，表明胶结物强度的降低是导致砾岩整体强度下降的主要原因。除了砾石颗粒和胶结物的力学性质外，砾石颗粒在基质中的比例也是影响砾岩力学响应的重要因素。研究表明[4]，砾岩的力学性能差异很大，具有极强的非均质性和各向异性，其物理性质受颗粒的大小、形状、胶结物性能等多种因素的影响，要确认某一个特定参数对整体结果的影响非常困难[5-6]。

基于离散元方法的数值模拟能很好地模拟岩石的力学行为，控制试样的各种变量，具有较强的可操作性和对比性。Cudall等[7]基于分子动力学提出了适用于岩石力学的离散元方法。随着计算机技术的发展，越来越多的学者使用离散元方法分析砾岩的力学性质。侯冰等[8]对砾岩地层的粒度分布进行了统计，利用颗粒流软件PFC2D模拟了井眼附近砾岩地层的破坏过程，分析了砾石分布对围岩破坏和井周裂缝扩展特征影响。刘向君等[9]利用离散元方法构建含有砾石的二维模型，研究了砂砾岩中裂缝扩展的过程，讨论了砾石强度对裂缝扩展机制的影响。相对于其他岩石或者地质材料，砾岩数值模拟多使用圆形颗粒的二维模型，没有考虑砾石形状对岩石力学性质的影响，存在一定不足。

为此，使用三维激光扫描技术获得砾石颗粒真实形态；基于离散元方法，建立含小、中、大3种不同粒径颗粒的三维数值模型，对数值模型开展单轴抗压实验，记录岩样的峰值强度、弹性模量、泊松比等力学参数以及加载过程中产生的颗粒位移、胶结状态等；对比均质岩心，得到了砾岩破坏形式和规律，分析了颗粒粒径大小和颗粒形态对砾岩力学性质的影响。研究成果可为进一步研究砾岩的力学性质提供理论依据和模型基础。

1 砾岩三维数值模型制备

1.1 颗粒流理论

颗粒流程序PFC3D根据颗粒离散元理论，采用显示差分算法，遵循牛顿运动定律和力-位移关系来模拟颗粒之间的相互作用和运动过程[10]。该方法将岩石模拟为离散颗粒的集合体，岩石的宏观力学性质是从单个颗粒的运动和相互作用中获得的，这种方式更加符合颗粒状岩石的性质。PFC3D以时间为基础，计算很小时间步长内颗粒的力和位移等信息。因此，不仅能得到的数值模拟的结果，还可以将力、速度、位移以及微裂缝等信息在整个模拟中的变化过程记录下来。

颗粒流模型由许多分散颗粒(ball和clump)通过具有相互作用的“键”(bond)来连接来组成。bond分为两种，一种只能传力，另一种由类似弹簧阻尼的系统组成，除了可以传递力之外，还可以传递力矩。PFC3D提供的球形颗粒(ball)可以用来描述砾岩中的石英砂及胶结物基质。“聚粒”(clump)是由许多球体(pebble)聚集而成，他们相对位置固定，在计算过程中只会计算clump与周围颗粒的相互作用，组成clump颗粒间的计算则被跳过，所以clump在外力作用下并不会发生破坏和解体。

1.2 砾石颗粒建模

目前，砾岩的数值模拟大多数都采用规则的圆形颗粒来表示砾石颗粒，但天然的砾石大多形态各异，砾石颗粒的形态对砾岩的岩石力学性质有明显的影响。随着三维激光扫描技术的发展，可以更加方便地获取砾石颗粒的三维形态，并导入离散元中建模。基于真实颗粒形态的三维建模相对比较复杂、研究较少，建模方法具体如下。

首先，分别按照大、中、小3种不同粒径，随机选择一定数量的砾石颗粒。随后使用手持三维激光扫描仪(精度0.02 mm)对每一个样本进行高精度扫描，获取表面云点信息，通过软件处理为PFC可识别的格式，并按照颗粒的大小和形态进行编号和分类，部分形态如图1所示。最后将不同形态的砾石颗粒扫描文件导入PFC中，生成描述砾石颗粒的“聚粒”(clump)。

为了建立更加符合真实形态的砾石颗粒，研究影响砾石颗粒精度的因素。结果表明，其主要取决于ratio和distance两个参数。其中，ratio参数为组成clump的最小和最大pebble半径之比，取值在0～1，ratio越小生成clump所需要的颗粒越多，生成的模板精度更高；distance为描述clump光滑程度的参数，取值在90～180，distance越大颗粒光滑程度越好，生成颗粒所需要的pebble数目越多。

图2 PFC砾石颗粒模型Fig.2 PFC gravel particle model

如图2所示，当ratio=0.1，distance=180时，砾石颗粒几乎与真实形态一致，但是一个模板由35 212个pebble构成，计算量过大。经过试算ratio=0.2，distance=130时，颗粒形态比较接近于真实情况，pebble个数只有467个，保证了计算精度和速度。对所有扫描颗粒都按照ratio=0.2，distance=130的参数来生成PFC砾石颗粒模板库。

1.3 数值岩心制备

综合考虑计算效率和精度，采用0.55 mm的球形颗粒(ball)来模拟砾岩中的石英砂和胶结物[11]。使用建立的砾石模板库(clump)，按照粒径大小呈高斯分布的方式生成砾石颗粒。通常砾石颗粒和胶结物强度差距大，砾岩的破坏大多发生在胶结物基质和颗粒-胶结物界面处，颗粒本身很少发生破坏，因此用clump来模拟砾石颗粒是合理的。

在生成砾岩模型过程中，颗粒投放的空间逐步减小，投放进行到后期时计算量很大并且经常失败。采用直接投放的方式难以成功，所以使用颗粒膨胀法生成颗粒。在投放时先使用较小颗粒生成一定数量的ball和clump，再将颗粒分多次、逐步扩大目标体积。生成试样后，删除悬浮颗粒，使用低压进行伺服，保证模型的均匀性和致密性。清除颗粒力和位移等信息，施加黏结，开展单轴实验。

在颗粒流数值模拟中，加载速度不必和实验设置得一致，只要小于一定的数值，对结果的影响就比较小。参考文献[12]，加载速度设置为2×10-3m/s。在加载过程中记录轴向应力和应变、颗粒位移、裂纹数目等参数，方便后续分析。按照上述方法，生成了小、中、大3种基于真实砾石颗粒形态的数值岩心。如图3所示。

2 数值模拟实验分析

2.1 细观参数选取

在PFC3D中，提供了3种基本接触模型：接触刚度模型、滑移模型和黏结模型。其中黏结模型包括接触黏结和平行黏结模型，它限定了法向力与剪切合力的最大值。根据砾岩的结构组成特征，选取接平行黏结模型来进行模拟是恰当的。

在离散元模拟中，模型的细观参数并不能直接与岩石宏观力学参数相对应。为了获得与室内实验岩石力学性质相近的数值模型，需要进行细观参数的标定。目前参数标定主要采用试错法，即通过对比物理实验和数值模型的结果，不断调整数值模型中的细观参数，使两者基本匹配[13-15]。基于已有的砾岩单轴试验数据进行宏观参数的标定。表1、表2分别给出了数值模型主要使用的细观参数、模拟与实验的对比结果。从表2可以看出，数值模型与室内试验结果在峰值强度、弹性模量、泊松比等力学参数上基本一致，误差很小。

蓝色小颗粒代表石英砂和胶结物，砾石由不同颜色的不规则大颗粒表示图3 砾岩数值岩心Fig.3 Numerical core of conglomerate

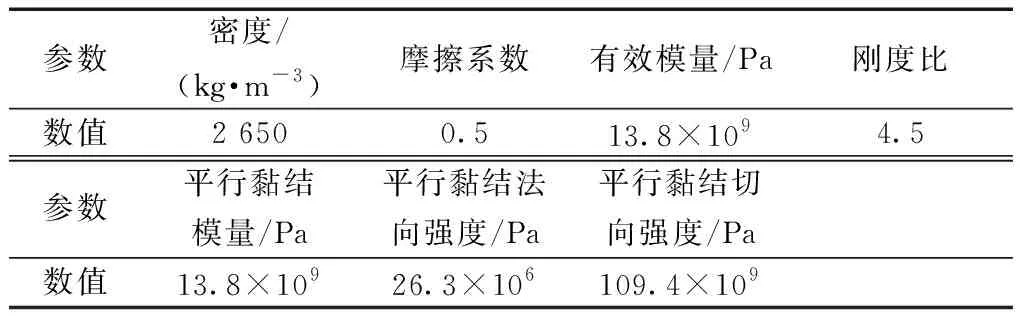
表1 模型主要细观力学参数Table 1 Main meso-mechanical parameters of the model

表2 模拟与实验结果对比Table 2 Comparison of simulation and experimental results

图4为砾岩室内试验和数值模拟的应力-应变曲线对比，可以发现：实验曲线存在明显的压密阶段，这是因为天然岩心内部存在一定的微裂缝和微空隙。数值模型经过伺服等手段，内部颗粒紧密且均匀，不存在这一过程。但整体上看，两条曲线在线性阶段斜率基本一致，峰值强度相同，都表现出较为明显的脆性破坏特征，取得了较好模拟的结果，细观参数选取合理。

2.2 破坏形式和机理分析

为研究砾岩的破坏形式和机理，分别对含砾和不含砾的岩心赋予相同的模型和参数，进行单轴抗压数值模拟实验。在数值模拟加载过程中，记录颗粒位移、胶结状态、微裂缝产生等数据，从而全面、准确的分析岩石的破坏形式和机理。图5记录了两种岩心的颗粒位移和胶结状态。

如图5(b)所示，在均质岩样的位移具有明显的规律性：岩样上部整体向右下方运动，下部整体向左上运动，上下两部分存在明显的类45°滑移面。在图5(e)中可以发现，含砾岩样的位移情况较为复杂：岩心上下两部分不再整体向某一方向移动，而是在被挤向岩心中部的过程中，由于砾石的影响和阻碍，分为左右两个部分，并向外移动。相对于均值岩心，砾岩岩心中部的颗粒向外运动的趋势更加明显，表现出较强的“鼓涨”现象。

图5(c)和5(f)记录了两种岩心的胶结破坏状态，其反应的岩石破坏情况与颗粒位移分析结果吻合。均值岩心中，形成了明显的类45°胶结破坏带，破坏带位置与岩样位移产生的滑移面一致。在砾岩岩心中，由于岩样位移情况较为复杂，胶结破坏的分布相对均匀，没有明显的破坏带；但岩样中部的胶结破坏比两端严重，这反映了颗粒位移分析结果中的“鼓涨”现象。

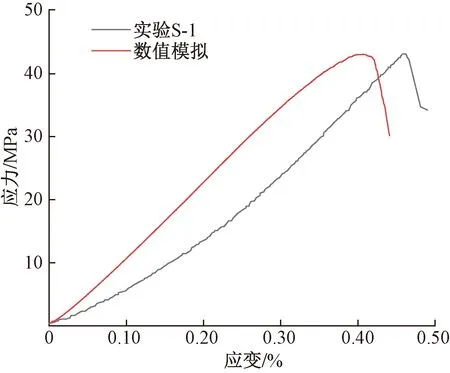
图4 应力-应变曲线对比Fig.4 Comparison of stress-strain curves

图5 岩样位移和胶结破坏图Fig.5 Rock sample displacement and cementation failure diagram

记录砾岩单轴抗压数值模拟试验中产生的微裂缝，并将微裂缝数量和轴向应力随时步变化情况绘制如图6所示。可以看出，在试样加载的初期几乎没有产生微裂纹；加载一定时间步长后，裂纹逐渐萌生但增加得较为缓慢；在应力峰值附近微裂纹数目急剧增加，形成贯通岩心的宏观裂缝，岩样瞬间破坏。

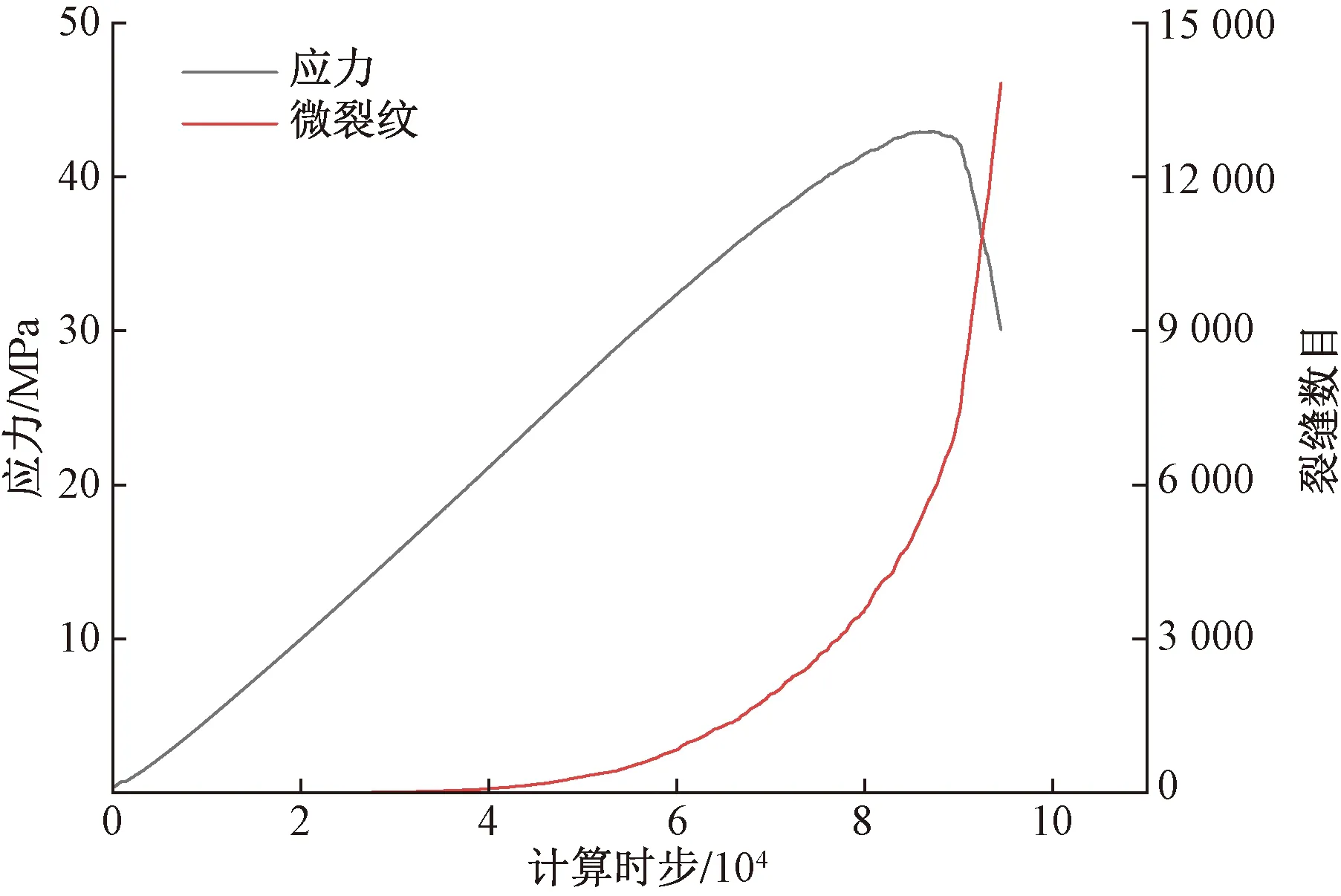
图6 裂纹、应力随时步变化Fig.6 Crack and stress changing with time

因此，砾岩的破坏形式和机理可以描述为：在施加轴向荷载的情况下，砾岩两端分别向岩心中部移动，由于基质和砾石刚度存在较大差异，砾石-基质界面形成应力集中区域，产生微裂缝；同时在砾石颗粒的阻碍下，微裂缝绕过必须绕过砾石颗粒逐步贯通，从而导致砾岩各部分的位移和破坏情况十分复杂；在接近应力峰值时，微裂缝急剧增加并贯通，岩样瞬间破坏，形成较为复杂的宏观裂缝，并表现出较为明显的“鼓涨”效应。

2.3 颗粒形状对力学性质的影响

将不规则砾石颗粒使用当量直径相同的球形颗粒代替，生成三维离散元数值岩心。对球形和真实形态的砾岩岩样分别开展单轴压缩实验，分别记录两种岩心的颗粒位移和胶结破坏情况如图7所示。两种岩样的位移趋势和胶结破坏分布基本一致，表明颗粒形状对破坏形式和机理的影响相对较小。然而圆形砾石岩样的整体位移明显大于非规则砾石，同时在胶结破坏较少时就发生了岩样破坏。这表明圆形砾石岩样的强度要低于不规则砾石颗粒岩样。

图7 岩样位移和胶结破坏图Fig.7 Rock sample displacement and cementation failure diagram

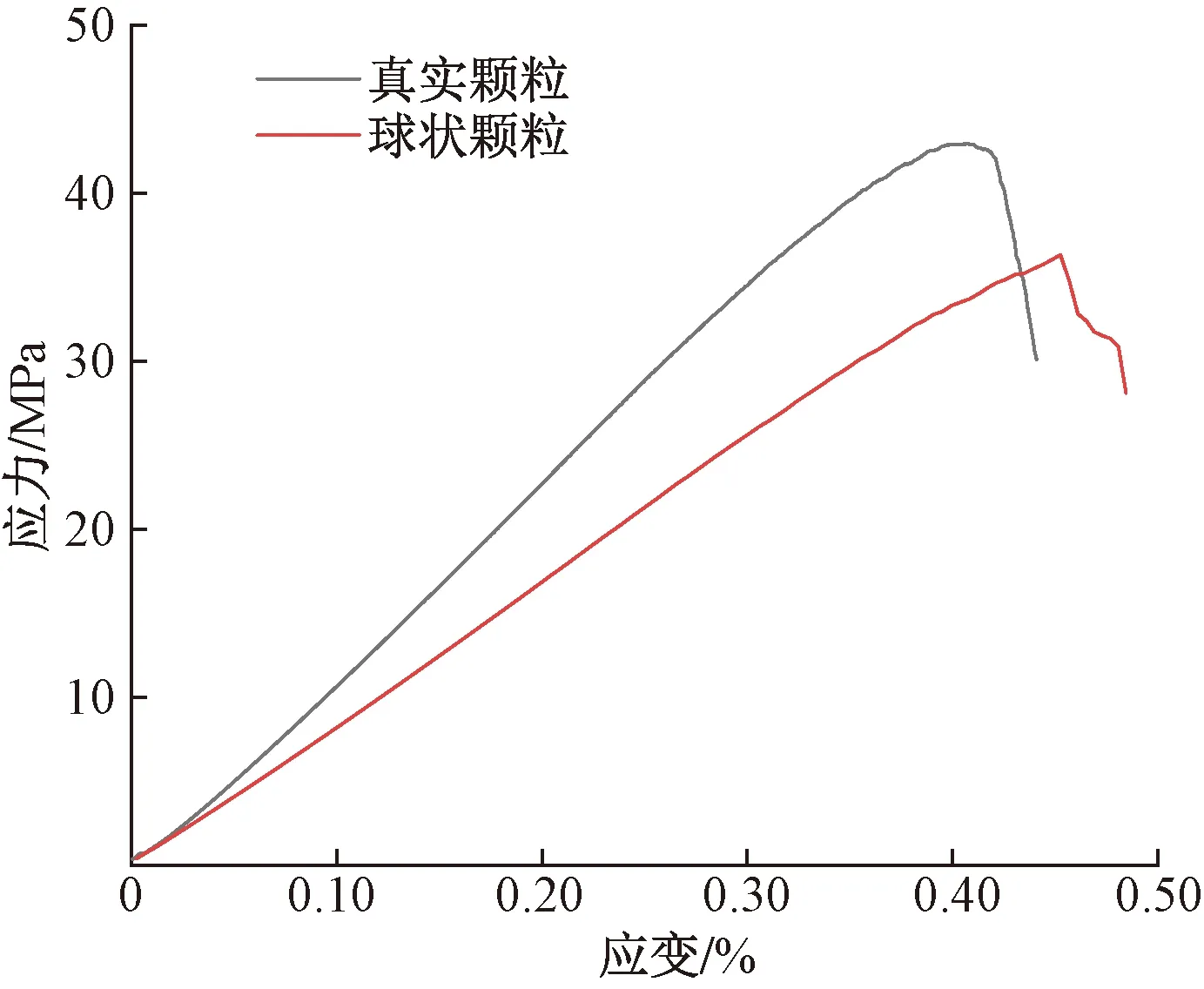
图8 不同形状颗粒应力-应变曲线Fig.8 Stress-strain curves of particles with different shapes

绘制两种岩样的应力-应变曲线，如图8所示。可以发现，含不规则砾石岩样的曲线峰值比球形砾石岩样提前到达，弹性模量和强度都有较为明显的提升，这与对颗粒位移和胶结破坏状的分析一致。形成上述现象的原因主要是：引入真实形态的砾岩模型在加载过程中，不规则的砾石颗粒会相互接触，彼此之间形成摩擦、咬合或嵌套等作用力，使得岩样承的载能力增强；而圆球形的砾石容易发生旋转和错动，不能很好地模拟砾石间的摩擦力。因此，砾石的真实形状能够显著增强砾岩的抗压强度，数值模拟中引入砾石颗粒的真实形态才能更好地反映和模拟砾岩的力学性能。

2.4 粒径对力学性质的影响

对含不同粒径砾石颗粒的岩心赋予相同的细观参数，开展单轴抗压实验，模拟结果如表3所示。

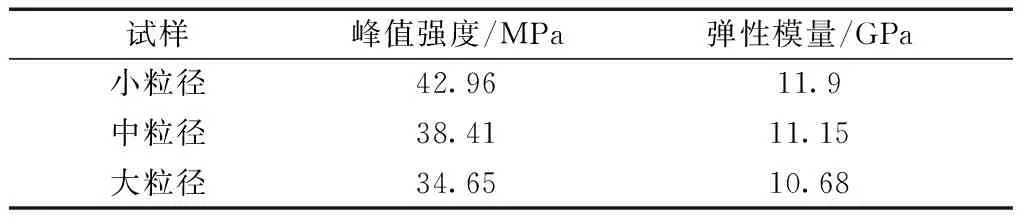
表3 砾岩数值模拟结果Table 3 Numerical simulation results of conglomerate

可以发现，随着砾石粒径的增加，数值岩心峰值强度和弹性模量降低。这主要是因为：在相同体积分数下，砾石颗粒粒径越大，其比表面积越低。而比表面积越大，砾石-基质界面黏结性能越好，受力更趋均匀，砾岩强度也越高。分析岩样的颗粒位移和胶结破坏情况，不同粒径岩样没有明显的差异，破坏过程和形式与前文基本一致，粒径对砾石破坏形式和机理影响不大。

3 结论

基于三维激光扫描技术和离散元建模方法，构建了含有不规则砾石颗粒的砾岩数值模型。对不同粒径和形态的数值模型开展单轴抗压实验，得出如下结论。

(1)由于砾石颗粒的阻碍，岩样的位移和破坏形式较为复杂；在加载初期裂纹数目少、增加缓慢，在应力峰值附近裂纹迅速增加，岩样瞬间破坏，表现出较为明显的“鼓涨”效应。

(2)砾石颗粒粒径和形状对砾岩的破坏机理和形式影响不明显，但随着粒径的增加，砾岩单轴抗压强度和弹性模量降低。

(3)相对于圆形颗粒，考虑真实形态的砾岩模型，能够反应砾石间的摩擦，拥有更高的强度和弹性模量，引入颗粒真实形态才能更好地模拟砾岩的力学性质。研究成果可为进一步研究砾岩的力学性质提供理论依据和模型基础。