基于小波变换的RBFNN与LSSVM高铁客流量组合预测
耿立艳, 胡 瑞, 张占福
(1.石家庄铁道大学 经济管理学院, 石家庄 050043;2.石家庄铁道大学 四方学院, 石家庄 051132)
0 引言
高铁客流量的准确预测对于相关部门科学制定运输方案、合理配置运输资源、规划高铁发展、调整高铁企业内部投资机构及经营管理具有重要作用[1]. 此外,高铁客流量的准确预测还有助于了解高铁旅客客流趋势、冷热门线路以及节假日出行变化等具体情况,对高铁票价的合理制定以及提高高铁客运服务能力等具有重要的实际意义.
高铁客运系统是一个复杂的不确定系统,影响高铁客流的因素很多[2],包括经济发展水平、铁路基础设施状况、人口数量、居民消费水平、旅行费用和其他替代运输方式的发展等. 因此,高铁客流量具有复杂性、随机性和周期性的特征,高铁客流量的预测属于复杂的非线性系统问题,难以用单一预测方法获得精确的预测结果.
目前常用的高铁客流量预测方法主要有:①线性预测模型,如时间序列分析模型[3]和回归分析模型[4-5];②非线性预测模型,如小波预测模型[6]和混沌预测模型[7-8];③人工智能预测模型,如神经网络[9]和支持向量机[10]等;④组合预测法,包括2种方法的组合及多种方法的综合[11]等. 线性预测模型通常以数学理论和假设为基础,通过演绎推理建立数学模型,建模简单,但难以描述高铁客流量复杂非线性变化,无法完全获取高铁客流量的内在特征. 非线性预测模型可刻画高铁客流量呈现出的非线性特征,但是高铁客流量数据所具有的海量小粒度的特征,将导致非线性预测模型的精度不高. 人工智能预测模型在数据处理过程中会产生“过学习”和“欠学习”问题[12]. 组合预测法将不同预测模型进行组合,可有效发挥单一预测模型的优点、弥补其不足之处,从而达到改善高铁客流量预测精度的目的. 神经网络是一种数据驱动的非参数预测方法,具有自组织、自学习能力、非线性逼近能力[13],其中,径向基神经网络(radial basis function neural network,RBFNN)具有较好的逼近能力、较快的学习能力和较强的分类能力,被广泛应用到模式识别、图像处理、时间序列分析、语音识别、智能控制等多个领域[14]. 但RBFNN存在训练速度慢、易陷入局部最优和“维数灾难”等缺陷[15]. 基于统计学习理论构建的支持向量机(support vector machines,SVM)通过结构风险最小化准则提高泛化能力,能较好地解决小样本、非线性数据、局部极小和“维数灾难”等问题[16]. 而高铁客流量正是有限样本数据,并且具有非线性、非稳定性等特征,因此采用SVM预测高铁客流,可对数据样本的非线性及随机性特征进行准确描述,以此来提高预测的精度. 但是标准SVM本质上求解的是二次规划问题,实际应用中将遇到求解速度较慢,求解参数较多等问题. 最小二乘支持向量机[17](least squares support vector machines,LSSVM)是SVM的改进与扩充形式,把求解二次规划问题转化成求解一组线性方程组,降低了计算复杂性,提升了运算速度和性能,更适合应用于高铁客流量这一复杂系统的预测问题.
本文提出的基于小波变换的RBFNN与LSSVM高铁客流量组合预测方法,融合了小波变换技术、RBFNN和LSSVM三种方法的优势,以提升高铁客流量的预测准确性. 首先利用小波变换技术的多尺度分辨特征,将高铁客流数据序列分解成低频趋势分量序列和高频随机分量序列;其次,2种分量序列分别采用RBFNN和LSSVM方法展开预测;再次,将2组单一模型得出的预测值合成为最终预测值;最后以我国某高铁站的日客流量为例,验证该方法的有效性.
1 基于小波变换的RBFNN与LSSVM组合方法
1.1 小波变换
小波变换是数据处理过程中常用的一种时频多分辨率分析方法,对于某一时间序列f(t)∈L2(R),连续小波变换可定义成:
(1)
式中,Wf(a,b)为小波变换系数;φ(t)为复共轭母小波函数;a为频率参数或尺寸参数;b为时域参数或平移参数.
对于离散数据序列f(nΔt),小波变换系数变为:
(2)
式中,Δt为采样间隔;n为样本容量.
小波变换系数可同时反映时域参数b和频率参数a的特性[18],当a较小时,数据序列f(t)是高频小波,取样步长小;当a较大时,f(t)是低频小波,取样步长大.另外,在时间序列转分解为小波系数后,根据高频部分呈现出频率分辨率较低、时间分辨率较高;而低频部分则与这一特征相反,可对小波变换系数进行进一步分析,这就完成了对时间序列的多尺度局部细化分析.
由于小波变换主要有连续和离散2种形式,而高铁客流量的时间序列表现为离散形式,所以需要对其进行离散小波变化.对高铁客流量进行小波分解与重构时,可选择快速算法——二进正交小波变换(Mallat算法)[19],利用该算法可快速完成高铁客流量数据序列的分解与重构.
cj+1=Hcjdj+1=Gcj(j=0,1,…,J)
(3)
式中,H和G表示分解低通和高通滤波器;c0为原始的离散数据序列.将c0代入式(3)进行分解,可生成c0在分辨率2-j的细节信号和逼近信号,也就是cJ和d1,d2,…,dJ.
在上述分解中,由于需要进行多次分解才能完成最终分解,而细节信号和逼近信号会随着分解次数的增加而减少,并且这种减少将不利于预测,为避免这一问题的影响,可采用重构算法实现信号重构:
(4)

1.2 径向基神经网络
RBFNN是以径向基函数作为隐含层函数的3层前馈神经网络,通过局部逼近与局部响应的原理实现网络训练[20],因其全局逼近能力较强,所以它可避免陷入局部最优,除此之外,它还具有收敛速度快,自适应性强和泛化能力强等特点,所以被广泛应用到非线性优化、时间序列预测等领域.
RBFNN共有3层,第1层是输入层,该层有多个感知节点组成,仅用来输入样本时间序列;第2层是隐含层,该层由多个径向基函数构成的隐含层节点组成,节点数与输入样本数相同,通过这些节点来对输入序列进行变换,通过局部响应的形式将处于低维的向量变换到高维空间中,使各节点产生较大输出,将低维的线性不可分问题转变成高维线性可分[21];第3层是输出层,该层由多个输出层节点组成,是对输入数据序列做出的响应结果,最后输出是这些节点输出的线性加权和:
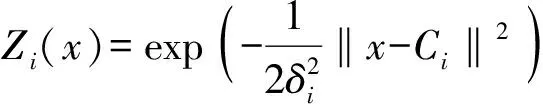
(5)
式中,x为输入的n维样本向量;Ci为第i个基函数的中心,与x维数相同;δi为高斯函数的方差,决定了基函数中心点的宽度.
RBFNN的输入与输出之间关系可表达为:
(6)
式中,ηi为第i个径向基函数的输出权重;Yi为第i个预测值.
1.3 最小二乘支持向量机
LSSVM是由SVM发展起来的新型支持向量机,它的基本思想是将SVM的二次规划问题转变为求解线性方程组,以减少模型计算的复杂性[22].具体模型构建原理如下:
将时间序列样本(xi,yi)i=1,2,…,N,定义为 1组对应的输入向量和输出变量,N是数据样本个数,通过非线性映射函数Ψ(x)=(Φ(x1),Φ(x2),…,Φ(xn))可将输入向量x映射到高维特征空间:
y(x)=wΨ(x)+u
(7)
式中,w为权重向量;u为偏差量,为常数.
按照结构风险最小化原则,将LSSVM优化问题定义为:

(8)
式中,γ为正则化参数,且大于0;ξj为误差项.求解以上优化问题时,可构造成拉格朗日函数,根据KKT条件,获得LSSVM回归函数形式如下:
(9)
式中,αi为拉格朗日乘子;K(x,xj)为满足Mercer条件的核函数,通常情况下有线性函数、径向基函数、多项式函数和Sigmoid函数[23]等形式.通过实证研究发现,RBF函数的泛化能力强,常被选用作为LSSVM的核函数:
(10)
式中,σ2为核函数的参数.当选用RBF函数作为核函数时,LSSVM的性能主要取决于参数组合(γ,σ2)的取值.
1.4 wavelet-RBFNN-LSSVM模型
高铁客流量的影响因素众多,导致其时间序列呈现出季节性、长短期变化. 除此之外,高铁客流量时间序列还具有周期项和趋势项的混合叠加特征. 单一模型只包含高铁客流时间序列的部分信息,难以全面反映各种规律的叠加影响,同时,短期规律对高铁客流量的影响也会被一定程度的削弱. 因此,可利用小波变换对客流量数据序列进行分解,使高铁客流量随时间变化的规律在不同频率上体现出来,再选取不同的方法进行预测,以实现高铁客流量预测精度的提高.
基于小波变换的高铁客流量组合预测方法(wavelet-RBFNN-LSSVM)的建模思路为:首先,通过小波变换技术将高铁客流量数据序列转换为2种序列:低频趋势分量序列与高频随机分量序列;其次,低频趋势分量序列具有周期性、线性特征,运用RBFNN进行建模与预测,高频随机分量序列具有随机性、非线性震荡的特征,通过LSSVM进行建模与预测;最后,将2组预测值叠加为最终组合预测值.
基于wavelet-RBFNN-LSSVM的高铁客流量预测步骤设计如下:
步骤1:数据预处理. 高铁客流量数据序列的波动变化幅度较大,若直接进行计算,将影响模型的运算速度和预测精度. 为了提高预测精度、加速模型收敛,先将高铁客流量数据序列进行归一化预处理,再采用边缘数据向外对称延拓法在高铁客流量数据序列的两端向外延拓2J个数据.
步骤2:小波分解与重构. 利用小波基对高铁客流量数据序列进行J尺度的小波分解及重构,去除高铁客流量数据序列数据前后延拓的数据,得到序列组{AJ,D1,D2,…,DJ}.
步骤3:单一预测. 设定RBFNN参数,选取LSSVM核函数并设定正则化参数与核数值;将全部数据样本分为两部分:训练样本集与检验样本集,基于训练样本集,构建RBFNN和LSSVM,利用RBFNN预测低频趋势分量序列{AJ},通过LSSVM分别预测高频随机分量序列{D1,D2,…,DJ}.
步骤4:组合预测. 将获得的低频趋势分量序列预测值和高频随机分量序列预测值叠加为预测值,再将预测值逆归一化为原始高铁客流量的最终组合预测值.
2 实例分析
2.1 小波数据分解
选取某高铁站的日客流量数据进行实证研究,将该高铁站2017年全年的365个日客流数据作为数据样本. 图1为某高铁站日客流量曲线图. 由图1可看出,某高铁站日客流量序列具有明显的随机性和波动性变动趋势.
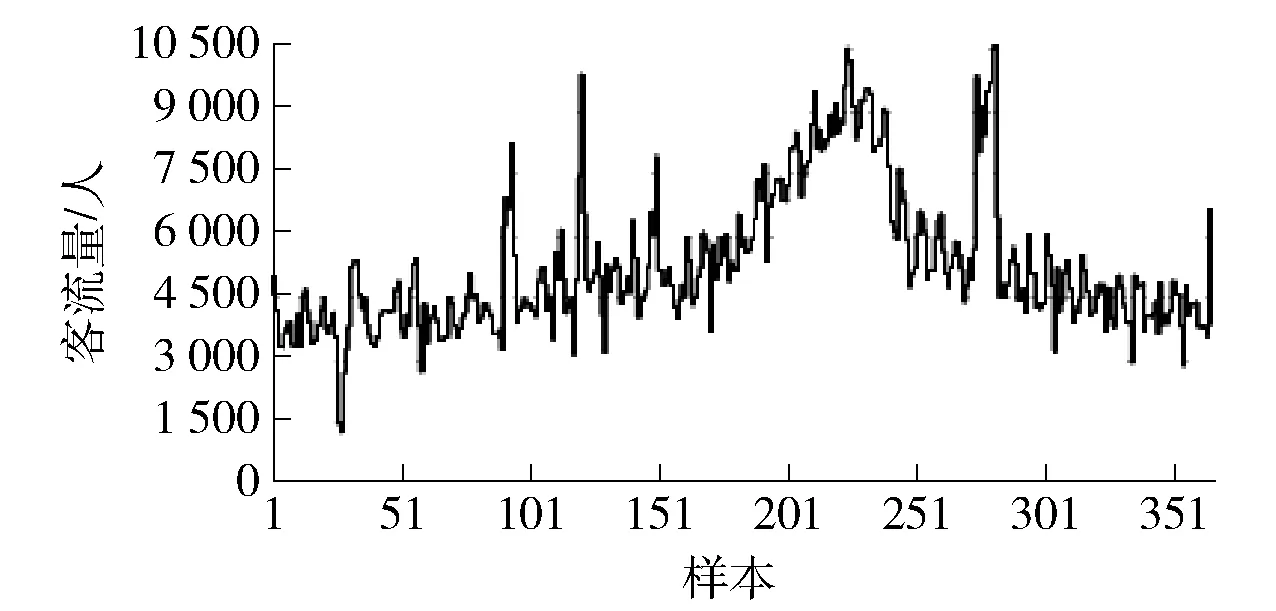
图1 某高铁站日客流量曲线图
将高铁日客流量数据序列看作一个复杂信号,利用小波分解进行复杂信号的频率分离. 首先确定小波基和分解函数. 由于高铁客流量数据序列具有明显的随机性与波动性,选择正交对称小波基以消除冗余. db小波具有正交性、紧支性、高正则性、高消失矩和具有Mallat快速算法等特点,db小波系列中,db4小波相对于其他小波具有更短的时窗和更高的时间分辨率,因此,本文采用时间序列敏感性高的db4小波基分解并重构高铁客流量数据序列. 基于小波变换能提取数据主要变化趋势和过滤随机信息的优势,通过Kolmogorov-Smimow方法确定高铁客流量数据序列分解与重构的尺度为3. 由于直接使用Mallat算法对高铁客流量数据序列作小波分解,会使得分解信号在边缘的数据产生失真,分解出的低频趋势分量序列与高频随机分量序列会产生交界,并且低频趋势分量序列与高频随机分量序列的预测值也会产生跳跃,最终导致预测结果的误差较大. 因此,在进行小波分解及重构之前,先利用边缘数据向外对称延拓法在高铁客流量数据序列的两端向外延拓8个数据,再使用Mallat算法的db4小波基对高铁客流量数据序列进行3尺度的分解及重构,最后去除高铁客流量数据序列前后延拓的8个数据,从而得到一个低频趋势分量序列{A3}和3个高频随机分量序列{D1,D2,D3},如图2所示. 小波分解的随机部分会和趋势分量会随着分解层数的增多而逐渐变的平滑,同时尺度部分规律性也在增强. {A3}已经比较光滑,保持了原高铁客流量数据序列的曲线形状. 因此,若先对原始高铁客流量数据序列进行小波分解,然后采用RBFNN预测{A3}、LSSVM预测{D1,D2,D3},再将上述预测值合成最终预测结果,从理论上可得到更加准确的预测结果.
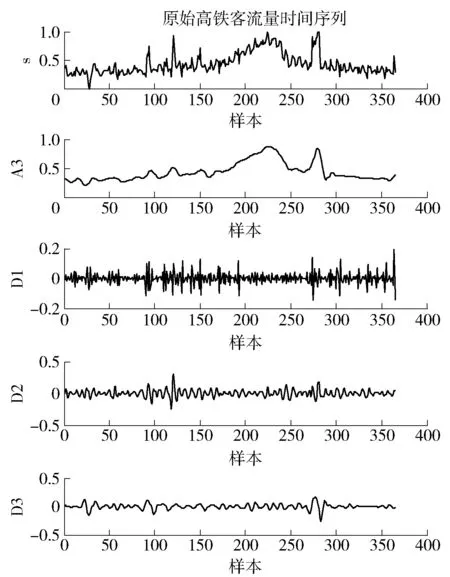
图2 某高铁站日客流量小波分解结果
2.2 神经网络与LSSVM预测
重构后的低频趋势分量序列和高频随机分量序列各有365个数据,分别将低频趋势分量序列数据和高频随机分量序列数据归一化到[0,1]区间. 并将2个分量序列划分成2组,前290个数据作为训练样本集,后75个样本作为检验样本集. 预测低频趋势分量序列{A3}时,基于训练样本集,构建RBFNN,RBFNN的最大节点数设为2,期望误差设为0.000 1. 利用训练好的RBFNN预测验证样本集. 预测高频趋势分量序列{D1,D2,D3}时,基于训练样本集,构建LSSVM,以RBF核函数作为核函数,通过5折交叉验证法确定参数组合(γ,σ2)的值. 运用训练好的LSSVM预测验证样本集. 最后,将得到的四组预测值相加获得高铁客流量预测值,并将得到的预测值逆归一化为原始高铁客流量预测值.
为验证wavelet-RBFNN-LSSVM的有效性,基本相同的数据样本集,利用RBFNN和LSSVM分别作为单一模型预测高铁客流量数据序列,再将两单一模型的预测结果与wavelet-RBFNN-LSSVM进行比较. 其中,RBFNN的最大节点数设为2,期望误差设为0.000 1;将LSSVM核函数选定为RBF核函数,采用5折交叉验证法确定参数组合(γ,σ2)的值.
2.3 预测结果分析
首先,利用均方根误差(root mean squared error RMSE)、平均绝对误差(mean absolute error,MAE)、平均相对误差(mean percentage error,MPE)、西尔统计量(Theil)、异方差调整的均方根误差(heteroskedasticity adjusted RMSE,HRMSE)对数损失函数(logarithm loss function,LLF)评价模型的预测性能. 表1列出了3种模型的预测性能比较. 由表1可看出,wavelet-RBFNN-LSSVM的RMSE、MAE、MPE、Theil、HRMSE、LLF值均小于RBFNN和LSSVM的对应值,说明wavelet-RBFNN-LSSVM的高铁客流量预测性能优于RBFNN和LSSVM,即本部分提出的组合预测法预测性能优于单一预测法. 另外,LSSVM的高铁客流量预测性能优于RBFNN,其6个预测性能评价指标均小于RBFNN的对应值.

表1 3种模型的预测性能比较
其次,采用M-Z回归检验评价模型的预测效果,回归方程如下:
yt=χ1+χ2t+randt
(11)
式中,yt为高铁客流量的实际值;t为高铁客流量的预测值;χ1和χ2表示回归系数;randt为随机项.回归方程的拟合优度R2值越大,表明高铁客流量的实际值与预测值越接近,则模型的预测效果越好.
表2列出了3种模型的M-Z回归检验结果比较. 根据表2,wavelet-RBFNN-LSSVM的拟合优度R2值为0.111 8,高于RBFNN的R2值1个数量级、高于LSSVM的R2值2个数量级,这充分证明,相比于RBFNN和LSSVM,wavelet-RBFNN-LSSVM对高铁客流量具有更好地解释作用,获得了更优的预测效果.
因此. 根据2种预测性能评价标准,基于小波分解的RBFNN与LSSVM智能组合预测模型相对于单一预测模型获得了更高的预测精度.
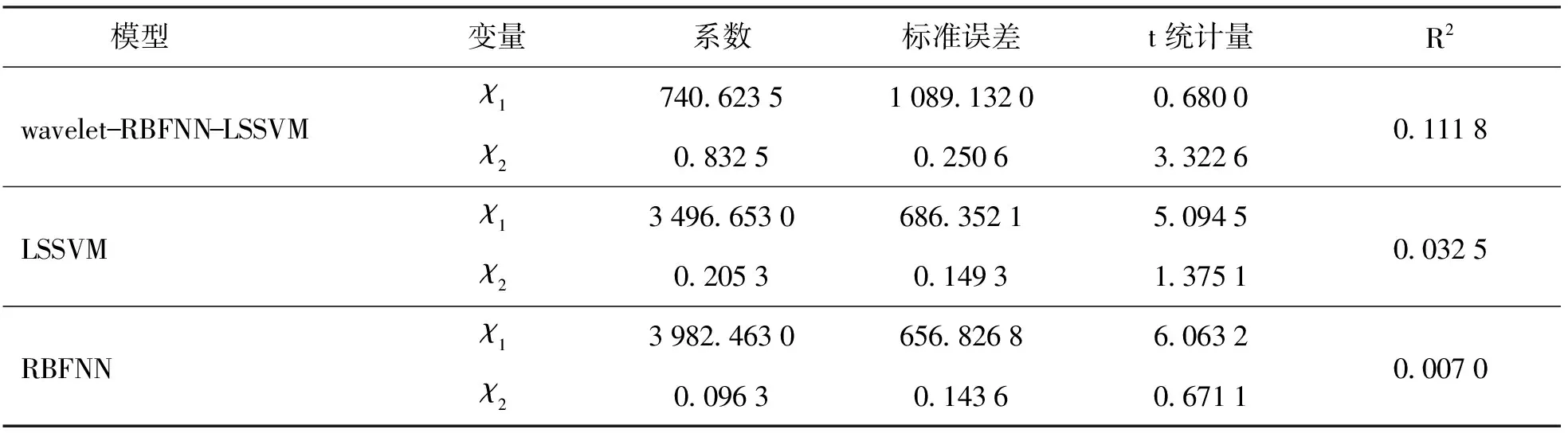
表2 3种模型的M-Z回归检验结果比较
图3为3种模型的预测值曲线图. 从图3可知,wavelet-RBFNN-LSSVM预测出了高铁客流量的长期变动趋势,RBFNN与LSSVM较好地预测出高铁客流量的波动变化规律. 在波动率变动幅度较小阶段,RBFNN与LSSVM预测效果相对较好,而在波动变动幅度较大阶段,wavelet-RBFNN-LSSVM的预测效果相对更优.

图3 3种模型的预测值曲线图
3 结束语
本文将小波变换、RBFNN、LSSVM相结合,提出基于小波变换的RBFNN与LSSVM组合预测法对高铁客流量进行预测. 先以小波变换分解出高铁客流量数据序列的2种分量序列,再分别利用RBENN和LSSVM预测2种分量序列,最后将这2种分量序列的预测值叠加为最终组合预测值. 根据2种预测性能评价标准,wavelet-RBFNN-LSSVM的RMSE、MAE、MPE、Theil、HRMSE、LLF值均小于RBFNN和LSSVM的对应值,且拟合优度R2值为0.111 8,高于RBFNN的R2值0.032 5和LSSVM的R2值0.007 0,相对于RBFNN和LSSVM的预测精度更高,适合于高铁客流量的短期预测.

