微网并入配网的双向灵敏度潮流置信评估算法

姚琪，纳燕钊，苏川，张浩然，曹宏飞，杨玉静

（国网宁夏电力有限公司吴忠供电公司,宁夏 吴忠 751100）

0 引言

大力发展新能源是实现能源可持续发展的有力举措。以光伏、风电为代表的新能源的发电功率受到环境影响，其输出功率具有一定的波动性与间歇性，大规模波动的功率并网会影响电网的潮流分布，并对电网的安全稳定运行带来一定的影响。微电网（以下简称微网）将多种分布式电源、储能、负荷等组合在一起，优先于本地消纳分布式发电单元的波动功率，因此，微网在一定程度上缓解了分布式电源发电功率的波动性对配电网的影响[1-4]。建立配电网的潮流灵敏度模型进而研究配电网中各个节点的功率变化对网络潮流分布的影响已经得到较多的研究[5-13]：文献[5]研究了一种宽适应性的潮流灵敏度分析模型，用于分析节点功率对配电网多种情况的影响；文献[6]基于多个灵敏度指标对电压稳定性进行评估；文献[7]基于灵敏度的方法对电网智能软开关进行分析；采用灵敏度分析也可以对新能源并入电网的各个状态进行建模与分析[8-10]，或者对配电网的运行模式等进行有效的计算[11-13]。在微网的潮流分析中，主要计及微网中的各个单元的运行模式，进而考虑微网中各节点的潮流分布情况[14]；另外，也有学者研究考虑微网中整体架构形式或者逆变单元的工作模式下的潮流计算方法[15-16]，以及微网中潮流的分布与微网的经济调度或者动态模式之间的联系[17-19]。有学者研究了将微网中可能发生变化的发电与用电单元作为不确定因素对微网功率潮流分布的影响，同时采用概率的方式建立潮流概率模型[20-21]。文献[22]引入全局灵敏度用于准确地分析影响微网运行的随机变量。关于新能源并入配电网后对潮流分布的影响，以及微网中功率潮流分布与不确定因素的影响在现有研究中已经取得了较多的成果，然而，当微网并入配电网后，微网中的各个单元的不确定性对配电网潮流分布的影响分析与概率评估，尚待进一步展开研究。

针对上述问题，本文考虚微网中的源网荷的各个不确定因素，对微网并网点的功率进行概率置信评估，建立配电网的双向灵敏度模型潮流置信评估算法。

1 微网的结构与原理

微网中含有多种形式的分布式电源，其中以分布式的光伏发电系统、风电系统为常见的发电单元，如图1所示。另外，在微网中一般设置储能系统用来平衡发电侧与用电侧，当微网并网运行时，若分布式发电单元的发电量小于负荷的用电量，则由储能系统或者公共连接点（point of common coupling，PCC）接入配电网，共同与分布式发电单元对负荷进行供电；若分布式发电单元的发电量大于负荷的用电量，多余电量则储存至储能单元或通过PCC点并入配电网。

图1 微网的结构

通过以上分析可知，微网内分布式电源的发电状态、负荷的用电状态、储能的荷电状态及其控制策略等可以看作微网内部的不确定性因素，其必然影响微网与配电网PCC点的功率流动，当PCC点的功率流动较大时，其对配电网内部的潮流分布造成的影响不可忽略。

2 基于置信区间的微网PCC点功率估计模型

微网中的各个分布式单元是微网中主要的发电单元，其输出功率受到气象因素的影响，具有波动性与间歇性；但其输出功率与负荷具有相同的可预测的特点，因此，基于对微网中分布式发电单元输出功率的预测与负荷预测，结合微网中储能系统的运行策略，可以得到微网与配电网并网点即PCC点的功率分布情况评估。

2.1 微网中分布式发电与负荷功率预测技术

对风电功率进行短时预测时，由于风电数据波动性较强且随机性大，因此，在风电功率预测中，首先对风电功率进行聚类处理，在不同的类别下，构建对应的预测模型。其中对风电功率数据按照波动程度进行聚类，风电功率波动程度提取方法如公式（1）所示[23]：

式中：k—功率波动趋势；

pwi、pwi-1—对应时刻twi与时刻twi-1的风电功率。

按照聚类算法对以上不同波动程度的风电数据进行聚类，聚类的距离公式为

式中：d ik—待聚类的第i个点的欧氏距离；

ki，kj—相邻的两个功率趋势数据;

n—功率波动趋势的个数。

采用Elman神经网络构建预测模型，并将各类功率数据对应的气象数据输入至预测模型中，对预测模型进行训练与预测，最终得到短时预测的风电功率Pw。

对于光伏功率与负荷功率进行预测时，由于光伏功率与负荷功率的波动性较小，其波动的随机性较弱，具有一定规律性，因此，直接采用深度学习模型等预测网络对历史的光伏数据与负荷数据进行训练与预测[24-25]，得到短时预测的光伏功率值为Ppv，负荷功率为Pload。

2.2 微网中储能系统的控制策略

微网中的储能系统对微网内部电源侧与负荷侧的功率起到平衡作用，储能系统在工作时，需要按照其自身的荷电状态决定是否充电或者放电，其荷电状态约束为

式中：Sstmin，Sstmax—储能系统放电与充电的下限与上限阈值。

微网内部的功率平衡，可以由以下公式表达：

式中：PPCC—PCC点的有功功率；

Pw—风电系统的有功功率；

Ppv—光伏系统的有功功率；

Pst—储能系统的有功功率；

Pload—负荷的有功功率；

QPCC—PCC点的无功功率；

Qw—风电系统的无功功率；

Qpv—光伏系统的无功功率；

QC—无功补偿装置的无功功率；

Qload—负荷的无功功率。

当微网内部的新能源发电量大于负荷用电量，且储能荷电状态允许充电时，则多余电量充入储能系统，此时Ppcc为零；当储能的荷电状态不允许充电时，多余电量则通过PCC并入配网中；当微网内部的新能源发电量小于负荷用电量时，储能系统可以放电，则由储能系统补充电量；当储能系统不放电时，则通过PCC从电网吸收功率，此时Ppcc大于零。

从以上分析可以看出，微网与配网PCC的功率分布情况与发电侧、用电侧、储能状态及其控制策略均有关系，因此，综合微网内部的功率流动状态，可以得到PCC点的功率变化情况。

2.3 基于功率预测的PCC点功率分布置信区间估计模型

由于风电功率预测值、光伏功率预测值、负荷预测值均存在一定的误差，单独考虑上述误差则不能统筹考虑系统内部多个系统的综合作用，且分析复杂；因此，本文功率预测按照微网中发电、用电、储能的运行特点，综合得到PCC点的功率分布估计值，如公式（5）所示：

根据历史测试集进行误差分析，得到误差的分布情况，以高斯分布进行拟合，并计算功率误差时间序列的平均值与方差，如公式（6）所示：

式中:ΔPi—PCC点的功率预测的绝对误差；

Δ—误差平均值；

n—功率序列长度；

σ—标准差。

在置信水平为（1-α）时，可以确定PCC点功率的值的置信区间为[26]

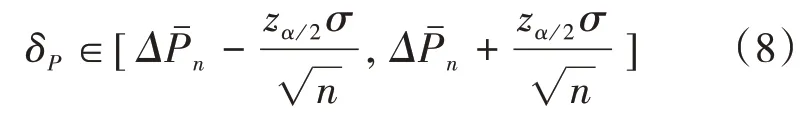
式中：—分位数。

把PCC点的功率预测值与预测误差区间结合，则可以得到功率预测的置信范围为

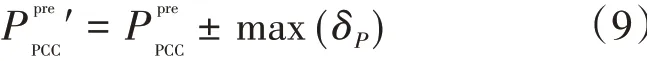
式中：—PCC处有功的置信功率；

th—某一时刻；

Δt—时间间隔。

进一步可以得到其他完整的灵敏度算法为

类似的，可以得到无功功率部分的灵敏度算法为

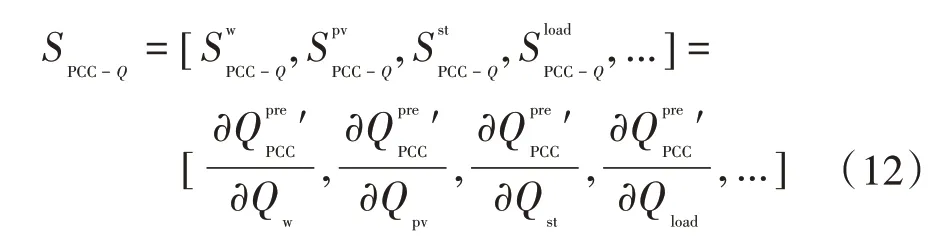
3 基于功率预测与置信区间的双向灵敏度模型

对于配电网，微网并入的节点是配电网中的一个特殊节点，节点的功率受到微网中不确定因素的影响，功率可能出现正与负，即对应于微网从配电网吸收功率与向配电网释放功率，该功率还可能随气候因素等方面的改变产生波动。

在对微网并入配电网的影响进行分析时，以潮流计算为基础，建立微网PCC点与配电网电压分布之间的灵敏度模型。对于微网并入配电网的i节点，节点功率与配电网节点电压的计算方程为[5-6,27]

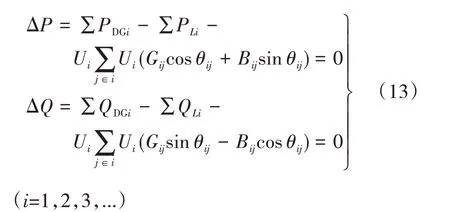
式中:PDGi—微网内部分布式电源发出的有功功率；

QDGi—微网内部分布式电源发出的无功功率；

PLi—负荷消纳的有功功率；

QLi—负荷消纳的无功功率；

Gij，Bij—线路参数；

Ui—电压幅值；

θij—电压相角。

经过级数展开并取线性项可以得到[27]：

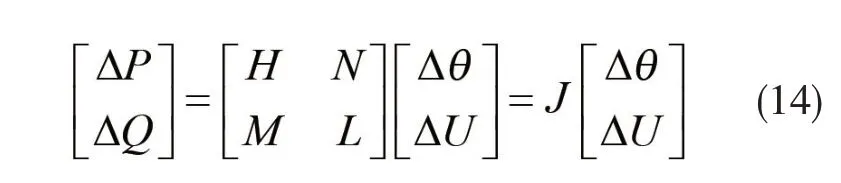
式中：H、N、M、L—雅克比矩阵的因素[27]。

如上节所述，Ppcc可以表征为置信区间的评估模型，这个功率受到微网内部的不确定因素的影响，同时又对配电网的各个节点造成影响，因此，基于置信度的配电网潮流灵敏度模型为

结合微网PCC点灵敏度模型，这个算法反映的是PCC点的功率波动对配电网各节点的潮流分布的影响，或者其表征了配电网中节点的潮流分布与PCC点的功率波动的灵敏度关系。结合上述PCC功率与微网中各因素的灵敏度关系，最终得到本文提出的基于置信度的微网与配电网双向潮流灵敏度算法为

4 算例验证

为了验证本文提出的双向潮流灵敏度模型，搭建了环形配电网模型，如图2所示。

图2 算例中配电网的结构

图2中的配电网为典型的环形配电网，其中包含3个节点，在配电网的拓扑形态上具有一定的典型性。在节点1处接入微网，即为微网与配网连接的PCC点。在微网中设置了50 kW的风电系统、50 kW的光伏发电系统、可变负荷等。在具体算例中，对微网中的风电系统、光伏发电系统、负荷的功率分别进行提前24 h的短期预测，预测功率曲线如图3所示。

图3 微网中典型12 h的功率预测曲线

如图3所示，微网中的新能源发电系统及负荷的功率均随着时间的变化发生波动，这种功率波动描述了微网中的不确定因素。在这种情况下，可以得到微网与配电网连接的PCC点功率波动，如图4所示。

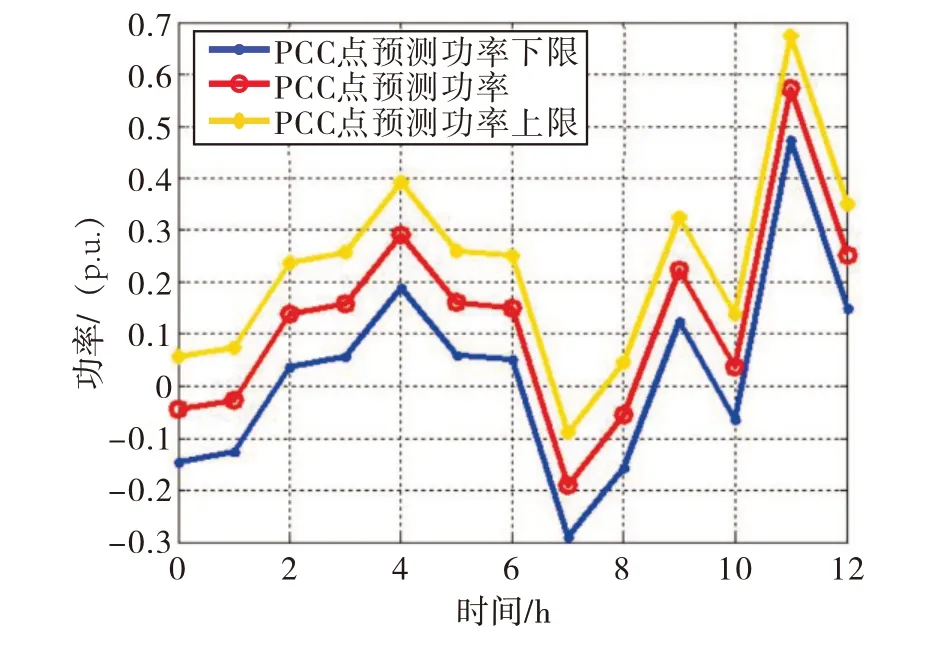
图4 PCC点典型12 h的功率置信区间评估

PCC点的功率波动主要是平衡微网内部发电侧与用电侧的供用电平衡。如前文所述，对风电系统、光伏系统负荷的功率进行预测时，均会有一定的预测误差，体现了微网运行工况的不确定性，但在微网内部运行时，由于发电侧与用电侧的融合，对误差具有一定的消解作用；因此，对PCC点的功率进行置信度估计，可以在一定程度体现微网中的不确定性。

图4体现了微网并入配电网的PCC点的预测功率的95置信区间，对PCC的功率起到概率评估的效果。在此基础上，根据本文提出的双向灵敏度模型，可以得到PCC功率对微网内各部分功率的灵敏度，此灵敏度体现了微网内部的不确定因素，对PCC功率概率评估的影响及对PCC点电压概率评估的影响，如图5所示。

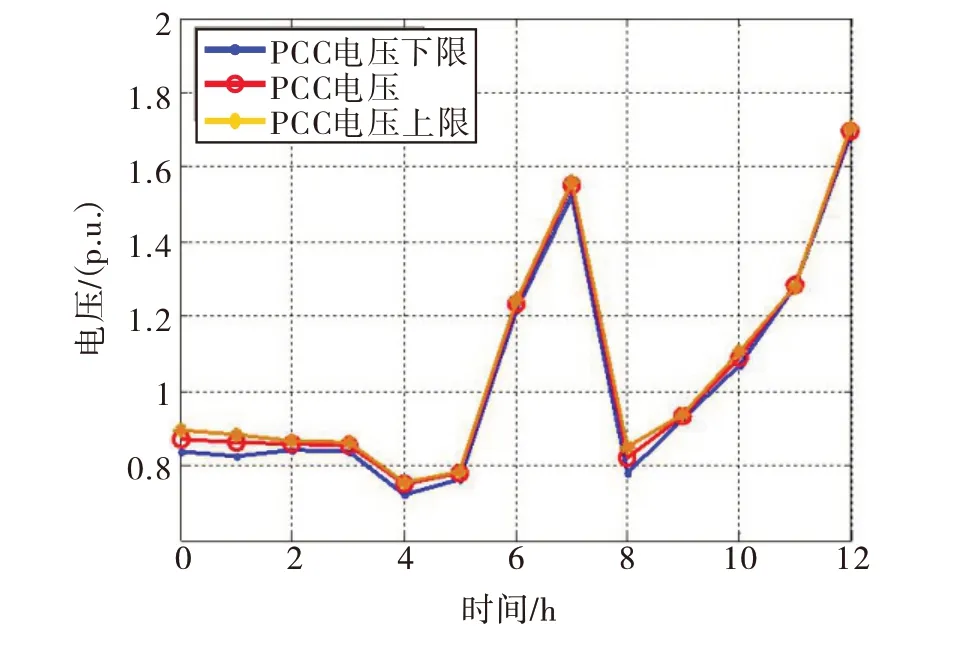
图5 PCC点置信区间电压波动评估曲线

根据本文提出的双向灵敏度模型，可以得到PCC功率对配电网中各节点的影响评估，如图6、图7所示。

图6 配电网节点1置信区间电压波动评估曲线

图7 配电网节点2置信区间电压波动评估曲线

各节点的电压变化，体现了配电网节点电压性能对P CC 点置信评估模型的灵敏度。

5 结论

提出了一种基于双向灵敏度的微网并入配电网潮流置信算法，其中包括基于预测的微网中源网荷侧及负荷的PCC点概率潮流置信算法，以及根据配电网结构建立的微网并入配电网的潮流评估算法。采用该双向灵敏度算法可以将微网中分布式电源发电与用电的不确定特征融入置信算法中，进一步通过微网并网的潮流评估算法反映在具体的配电网各个节点的潮流分布计算中，以置信区间的形式反映功率波动与节点电压波动情况，评估结果更为合理准确。该算法对微网及配电网的规划、设计具有较强的理论意义及实际应用价值。