设备间任务依赖的最佳卸载决策和资源分配
胡 恒,金凤林*,谢 钧,俞 璐,黄科瑾,孟繁伦,杨 涛
(1.陆军工程大学 指挥控制工程学院,江苏 南京 210007;2.陆军工程大学 通信工程学院,江苏 南京 210007;3.31121部队,江苏 南京 210018;4.61096部队,江苏 南京 210007)
0 引 言
随着物联网技术和5G技术的发展,产生的各种新型应用,对网络的时延和带宽提出了更高的要求。但由于终端设备的计算和存储能力的限制,无法处理和存储如此庞大的数据。因此移动边缘计算[1]应运而生,MEC能有效解决时延长、能耗高和数据不安全等问题。其中计算卸载技术[2]作为MEC的关键技术之一,通过合理的卸载决策和资源分配策略将终端设备上运行的任务卸载到边缘服务器,能够减少任务完成时延和设备的能耗,提高设备性能。而通过将D2D技术与MEC结合,可以更进一步降低数据传输时延和能耗。
对于计算卸载技术,目前已经出现了很多研究成果。文献[3]提出了一种低复杂度的启发式算法来最小化共享频谱中的任务执行延迟。文献[4]考虑了具有辅助节点的MEC系统,联合优化了用户和辅助节点的计算和通信资源分配,使总能耗降至最低。文献[5]基于一种低复杂度的算法来降低设备能耗。文献[6]使用线性规划的方法解决卸载决策、延迟和能耗联合优化问题。文献[7]为了最大程度地减少任务等待时间和能耗,提出了一种启发式算法,该算法保证了子任务之间的依赖性并提高了任务效率。文献[8]提出了一种基于Lyapunov优化的低复杂度的动态计算卸载在线算法,获得了最优的卸载策略。文献[9]考虑了包含多个忙碌智能设备和多个空闲智能设备的D2D与MEC协作系统,基于块坐标下降法和凸优化技术的两阶段迭代算法解决卸载决策和资源分配的联合优化问题,获得最佳卸载策略和资源分配策略,最小化系统的总能耗。文献[10]建立了一个具有通信资源和计算资源约束的混合整数非线性问题,开发了一种优化算法来解决此问题。文献[11-13]同样考虑了在MEC环境下引入D2D技术进行协作,来考虑任务的卸载情况。
然而以上文献都仅考虑了单个设备上任务的卸载情况。对于不同设备之间任务具有依赖性的研究非常少,几乎没有。实际上,在不同设备上执行的任务通常也是具有相关依赖性的。文献[14]虽然考虑了MEC系统环境下两个不同设备之间的任务相关性,但没有考虑与D2D技术进行协作来优化系统性能。虽然业内也在MEC环境中引入了D2D技术来优化系统性能,但是对于MEC与D2D技术协作网络环境中不同设备任务之间任务具有相关性的研究,就作者目前所知,还没有相关文献对此方面进行研究。因此该文针对此方面,同时在文献[14]的基础上进行了研究,联合优化了设备任务完成时延和能耗,在任务执行时延和设备能耗之间进行权衡,寻找一个平衡点使得系统性能最优。
1 系统模型
1.1 网络模型
考虑了两个设备的MEC与D2D协作网络。图1为MEC与D2D协作网络系统模型,其中d1和d2分别表示设备1、设备2与MEC服务器之间的距离,d3表示设备1和设备2之间的距离。
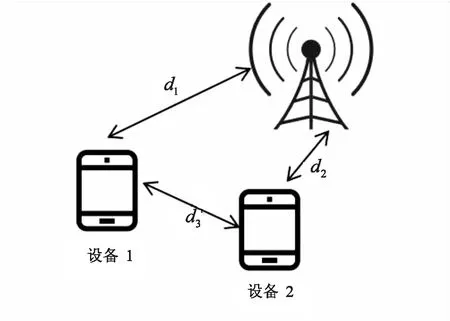
图1 MEC与D2D协作网络系统模型
设备1和设备2分别具有m和n个要执行的一系列任务,并将任务之间的依赖关系建模为顺序图,同时对每个设备引入两个虚拟任务,0为设备的输入任务,m+1和n+1为输出任务,如图2所示。其中设备2的第k个子任务的输入依赖于设备1第m个任务的输出和设备2第k-1个任务的输出。
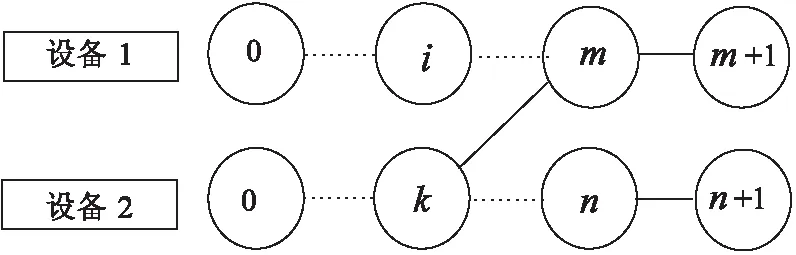
图2 不同设备间调用图模型
该文采用{Li,j,Ii,j,Oi,j}来描述每个设备的每个任务,其中j=1表示设备1,j=2表示设备2。i表示设备上的任务,i=0,1,…,m+1或0,1,…,n+1。Li,j表示任务的计算量,完成任务总共需要的CPU周期,Ii,j表示计算任务的输入数据的大小,Oi,j表示任务的输出数据的大小。对于设备1和设备2第0个和最后一个虚拟任务计算量为0。同时对于两个设备而言,第0个任务输入数据的大小为0,最后一个任务输出数据的大小为0。对于设备1和设备2第i个任务的输入等于上一个任务的输出:Ii-1,j=Oi-1,j,j={1,2},i=1,2,…,m,m+1或1,…,k-1,k+1,…,n+1。特别的是,对于设备2的第k个任务的输入依赖于设备2的第k-1个任务和设备1第m个任务的输出:Ii,2=Oi-1,2+Om,1。该文规定第0个和最后一个虚拟任务只能在本地执行。同时,用ai,j={0,1}表示卸载决策:ai,j=0表示在本地执行,ai,j=1表示在服务器执行。
1.2 通信模型
首先介绍了系统的通信模型。对于每个设备分配带宽相等的正交信道,用W表示,卸载和上传设备之间互不干扰。
上传速率为:
(1)
其中,pi,j表示设备j的发射功率,hi,j表示设备j到边缘服务器的信道增益,σ2表示设备的噪声功率。
下载速率为:
(2)
其中,p0表示边缘服务器的固定发射功率。
设备1与设备2之间的传输速率为(设备1第m个任务的输出与设备2的第k个任务有关):
(3)

信道增益为:
(4)
其中,g表示天线增益,Fc表示载波频率,dr表示距离,pl表示路径损耗指数。
1.3 计算模型
下面给出了执行和传输任务的时间和能耗。
本地执行任务i的完成时间为:
(5)
其中,fi,j表示执行任务i的CPU计算能力。
本地完成任务i所损失的能耗为:
(6)
其中,k是取决于芯片架构的有效开关电容参数,是固定常数。
服务器执行任务i的完成时间为:
(7)
其中,f0表示服务器的恒定CPU频率。
将任务i从设备传输到服务器的上传时间为:
(8)
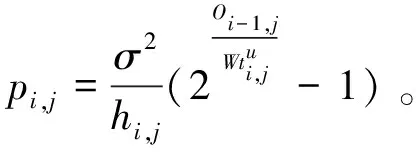
将任务i从设备传输到服务器的传输能耗为:
(9)
从服务器返回到设备的下载时间为:
(10)
将任务从设备1传输到设备2的传输时间为:
(11)
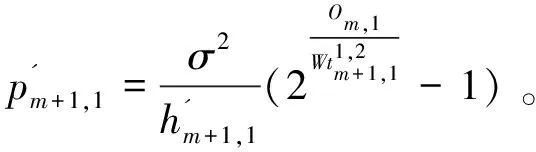
将任务从设备1传输到设备2的传输能耗为:
(12)
1.4 依赖模型
由于设备1的第m个任务的输出作为设备2第k个任务的输入,所以要综合考虑设备1第m个任务和设备2第k个任务的位置关系:当m任务和k任务都在本地执行时,由于两设备都支持D2D技术,所以设备之间可以直接通信,有传输时延和能耗;当m任务和k任务都在边缘服务器上执行时,此时没有时间和能耗的损耗;当m任务在本地执行,k任务在边缘服务器执行时,此时需要上传时延和能耗;当m任务在边缘服务器执行,k任务在本地执行时,此时需要下载时延。
1.5 问题公式化
由以上分析可知,设备1的任务完成时间为:
(13)
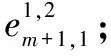
(14)
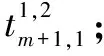
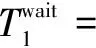
(15)
等待设备2第k-1个任务的输出时间为:
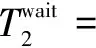
(16)
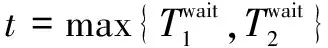
设备2的任务完成时间为:
(17)
设备2消耗的能耗为:
(18)
两个设备总性能指标为:
(19)
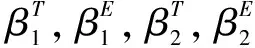
(20)
所以问题公式化为以下公式:
s.t.
(21)
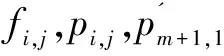
s.t.
(22)
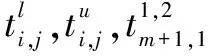
2 固定卸载决策的最佳资源分配
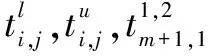
问题p(3)的拉格朗日表示为:
(23)
其中,λ和μ都是不小于零的表示与相应约束相关联的对偶变量,λ*和μ*表示最佳对偶变量,则能推导出每个设备的最佳CPU频率和发射功率的闭合表达式如下:

(24)
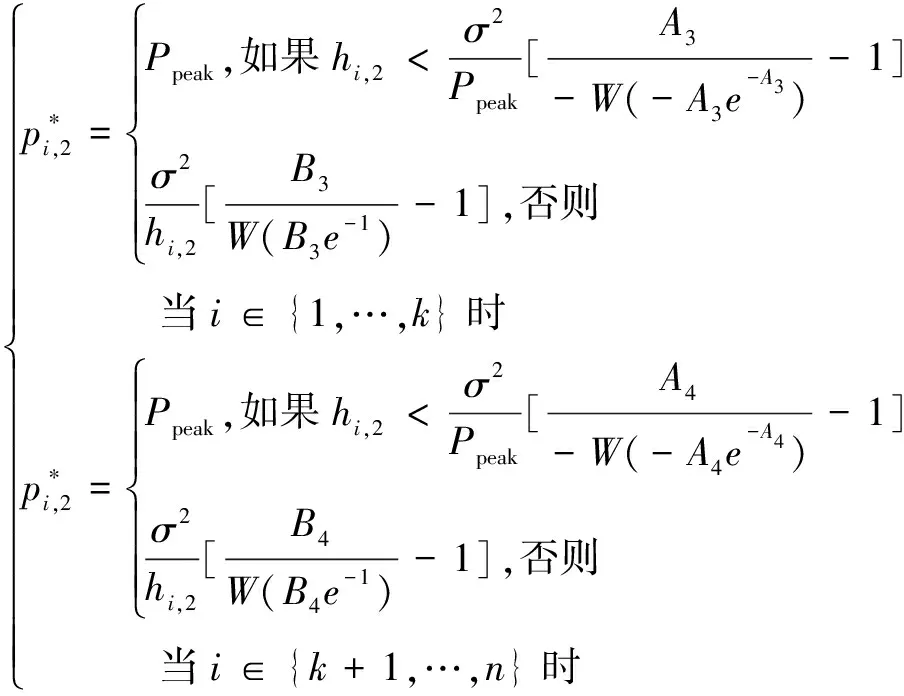
(25)
其中,
W(x)表示LambertW函数,应用梯度下降法迭代更新λ和μ,直到满足一定的停止标准。该方法的伪代码如算法1所示。由于P(3)是一个固定ai,j的凸问题,梯度下降法保证收敛。
算法1 :最佳资源分配算法。
1输入:给定大于0的λ和μ、步长α和精度值pre
2输出:p*,f*
3 while True:
4根据最佳CPU频率的闭合表达式(24)计算fi,j
5根据最佳发射功率的闭合表达式(25)计算pi,j
8根据梯度下降算法,分别更新λ和μ的值
10退出循环
11 End
3 优化卸载决策
在第2小节中,给定卸载决策,可以得出最佳资源分配,需要搜索2(m+n)次卸载决策,然后从中选择最小目标的卸载决策。但是随着任务m或n的增多,这种遍历搜索方法是行不通的,复杂度会很高。基于此提出了一种降低复杂度的在线任务卸载算法,可以在多项式时间内获得最优卸载决策。本节首先证明最优卸载决策具有连续性,然后在此基础上提出了一种降低复杂度的优化算法。
3.1 一次爬升策略
定理1:假设f0>fpeak,则最优卸载决策具有连续性(如果有任务要卸载),即对于最优决策,如果设备有任务需要卸载到边缘服务器,那么在整个任务的执行过程中,任务卸载到边缘服务器只会发生一次,它被称为一次爬升策略。
证明:略。
3.2 基于一次爬升策略的在线搜索算法
基于一次爬升策略,提出了低复杂度的在线任务卸载算法。通过此算法不必暴力遍历所有可行的卸载决策,只需在每个设备上寻找满足使得设备能耗和时间加权和最小这个指标要求的两个任务即可。如图3所示,找到满足指标要求的两个任务i和j,然后只需将i和j,以及中间的任务都卸载到边缘服务器即可。

图3 一次爬升策略
因此只需寻找这样两个任务,使得设备的能耗和时间的加权和η(i,j)最小。这里设定任务i*为入口任务,任务j*为退出任务,i=1,2,…,m,j=1,2,…,n,设备的能耗和时间加权和公式如下:
(26)
其中,eu为传输能耗,el为本地能耗,tu为传输时间,tc为在服务器上的执行时间,td为下载时间,tl为本地执行时间,βE和βT分别为能耗和时延权重,η(i,j)为加权和,ηmin为最小加权和。
算法2给出了寻找最优的入口任务i*和退出任务j*的算法,初始时,任务全部在本地执行。因此只需要枚举满足一次爬政策的卸载决策,而不必遍历所有2m+n个卸载决策,即只需在每个设备上寻找满足使得设备能耗和时间加权和最小这个指标要求的两个任务即可。对于设备1,根据算法2只需搜索m*(1+m)/2个任务组合。类似的,设备2也只需要搜索n*(1+n)/2个任务组合。因此搜索总数[m*(1+m)/2*n*(1+n)/2],即O(m2*n2)。随着m或n的增大,基于单爬策略的在线搜索算法的复杂度明显低于暴力搜索算法。
算法2:在线搜索算法。
1输入:给定βE,βT值
2输出:ηmin,i*,j*
3根据加权和公式计算η(1,1),令ηmin=η(1,1),i*=1,j*=1
4 Fori<----1 tom:
5 Forj<---itom:
6计算出最优f*和p*,然后计算设备的能耗和完成时间
7根据能耗、时间和加权和公式计算设备的加权和η(i,j)
8 Ifη(i,j)<ηmin:
9ηmin=η(i,j)
10i*=i
11j*=j
12 End
13 End
4 实验评估
在这一小节,将进行数值模拟来评估所提的卸载算法,关注的性能指标是两设备的总性能,用ET表示,其中每个设备的性能用设备完成任务所消耗的能耗和时间的加权和表示。为了方便与文献[14]算法进行比较,实验数据值的大小参考文献[14]进行了设置。接下来,将会用最优卸载算法和文献[14]中算法进行对比分析。
图4为每个设备的任务调用图,每个节点代表一个任务,节点权值为完成此任务的计算量,边权值表示输入和输出数据的大小。这里将设备的任务数量设置为m=3和n=5,服务器的发射功率固定p0为1 W,每个设备的发射功率峰值ppeak为0.1 W,边缘服务器的CPU频率fc和每个设备的CPU频率峰值fpeak分别为1010和108(cycles/s),噪声功率σ2为10-7W,k是取决于芯片架构的有效开关电容参数,是固定常数,这里设置为10-26。此外设置带宽W为2 MHz,对于每个设备上任务的计算量大小设置为Li,1=[0,65.5,40,3,96.6,0](Mcycles),Li,2=[0,70.8,95.3,86.4,18.6,158.6,0](Mcycles)。
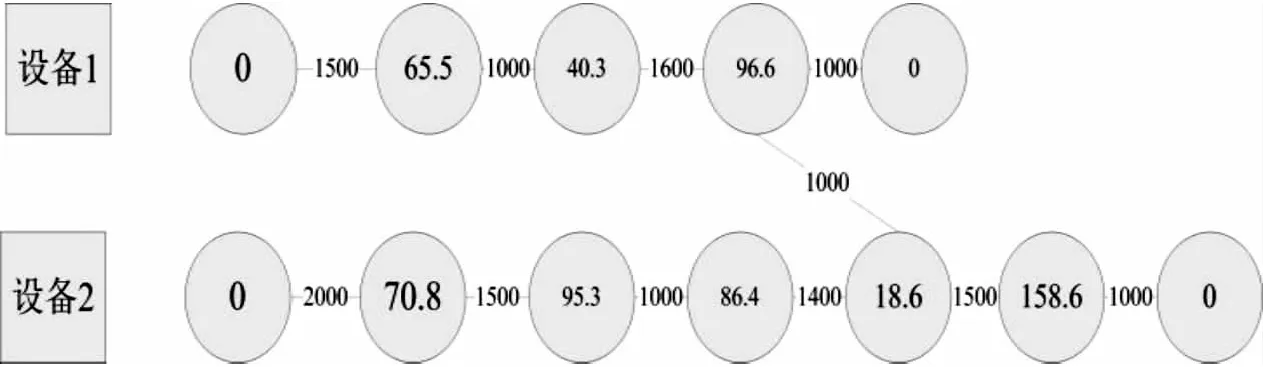
图4 实验模型和参数
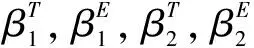
接下将与文献[14]算法下的系统性能做比较。在此次实验中由于文献[14]与本实验的最优卸载决策:设备1的第m个任务和设备2的第k个任务都是在边缘服务器执行,所以为了更好地对比最优算法和文献[14]中的算法,这里采用了相同的次优卸载决策,此决策中设备1的第m个任务和设备2的第k个任务都是在本地执行,这样能更直观地观察有无D2D技术支持系统性能的优劣。
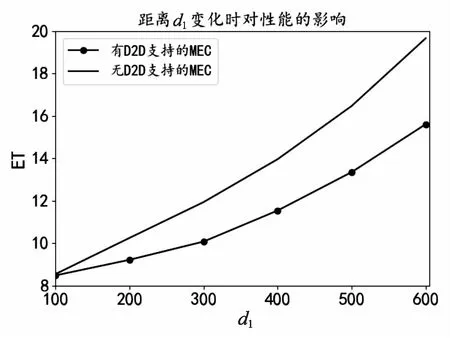
从图5中的(a)和(b)可以观察到,当固定d3和d2或固定d3和d1时,随着d1或d2距离的增大,该文提出的算法要优于文献[14]提出的算法,因为在支持D2D技术的MEC系统中,设备1的第m个任务和设备2的第k个任务都在本地执行,设备间之间可以直接通信,避免了在不支持D2D技术的MEC系统中需要先将任务卸载到边缘服务器,然后从边缘服务器下载到设备2上。所以可以得出支持D2D技术的MEC系统相比于文献[14]不支持D2D技术的MEC系统,节省了时间和能耗,系统性能更好
从图5(c)可以观察到,当d3增大时,文献[14]的算法不受d3距离变化的影响,是因为设备1的第m个任务和设备2的第k个任务都在本地执行,设备之间不需直接通信。虽然该文提出的算法受d3的影响,但是通过图(c)中曲线可以观察到,在两设备间的距离不大于设备到服务器之间的距离400 m时,该文所提的算法还是优于文献[14]所提的算法。而当两设备间的距离大于400 m时,任务卸载到边缘服务器上是较好的选择,因为边缘服务器的性能要比设备的性能好,将任务卸载到边缘服务器能节省能耗和时间。现实中也可以知道,当设备间的距离远大于设备到服务器之间的距离时,当然是卸载到服务器更好,但当设备间距离较近时,卸载到设备是更好的选择。
(a)
5 结束语
该文研究了MEC与D2D技术协作系统环境下不同设备之间具有任务依赖性的最优的资源分配和优化任务卸载决策问题。为了最小化设备的能耗和任务完成时间的加权和,首先固定卸载决策,推导出卸载发射功率和本地CPU频率的闭合表达式,运用凸优化方法求解出该问题的最优解,得到最佳资源分配策略。然后证明了最优卸载决策遵循一次爬升策略,在此基础上提出了一种降低复杂度的在线任务卸载算法,通过该算法获得了最优卸载决策。通过数值实验表明,提出的最优卸载策略明显优于其他算法。

