锁定已知 构建联系 设定未知 发展思维
——以“用一元二次方程解决问题”课堂教学为例
⦿江苏省无锡市江南中学 王 蕾
1 引言
“用一元二次方程解决问题”是苏教版九年级(上)第一章第四节的内容.在本章的前三节学生已经学习了一元二次方程的概念、解法,以及方程的解与系数的关系,对一元二次方程相关知识有了系统的认知.接下来通过探究实际生活中数量关系的过程,体会、体验一元二次方程解决实际问题的数学模型;同时,在运用一元二次方程解决现实生活中实际问题时,不仅要注意解方程的过程,还要检验所得的解是否符合问题的实际[1].
2 创设实际问题情境,引导学生进入课题
从字面上看“用一元二次方程解决问题”这一课题有两个方面的含义:一是运用的知识是一元二次方程,另一是解决的问题是现实生活问题.因此,把实际问题转化为数学问题,对现实生活问题进行数学建模,不仅仅是列出一元二次方程去求出问题的解,而且还要进行推理判断所得出的结果与生活实际是否相符,这是本课题的重点,也是本课题的难点.
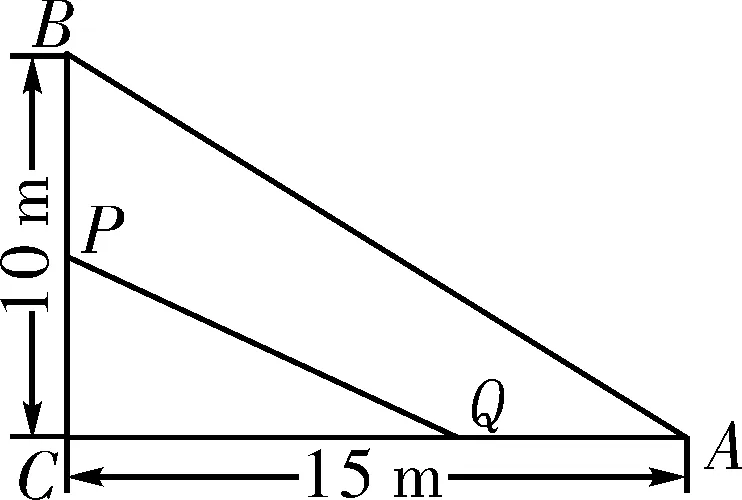
图1
导入情境(电子白板展示)如图1,Rt△ACB是一养鱼池的一角,∠C=90°,为了捕鱼,一渔网同时由A,B两点出发分别沿鱼池边缘AC,BC方向向点C匀速移动至点Q,P,它们的速度都是1 m/s,问多长时间后△QCP的面积为Rt△ACB面积的一半?
创设目的:为了让学生将实际问题具体化,在引入课题之时创设的问题情境用图象形式呈现,让生活问题具有“数学模型”化的特征,学生用数学方法建模就可以简单化.
3 引导探究解题过程,帮助学生对实际问题进行数学建模
“引导探究解题过程”“帮助学生进行数学建模”是帮助学生掌握应用一元二次方程解决实际问题的方法步骤,并且是提高分析问题、解决问题能力的关键.

教学案例1
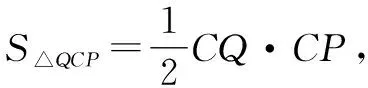
师:如何计算CQ,CP的值呢?
生:根据点A到点Q与点B到点P距离相等.(进行讨论、各抒己见.)
师:若点A到点Q的距离是xm,又怎样计算CQ,CP的值?
生:CQ=(15-x)m,CP=(10-x)m.
师:请同学们解决情境中的问题.
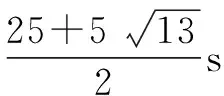
师:这两个数据都符合实际情况吗?
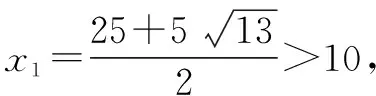
师:通过以上问题说明,利用一元二次方程解决问题不仅要求出具体数值,而且还要分析判断是否存在某种数量关系;同时,用一元二次方程解决实际问题时,不仅要注意方程求得的解是否正确,还要检验方程的解是否与问题的实际情境相符合.请大家思考上述解决问题的主要步骤.
学生:通过小组讨论,归纳总结出:
①从情境中找出存在的量的关系,列出等式;
②在列出的等式中发现未知量,设定未知数;
③将设定未知数代入列出的等式中进行求解;
④检验所得出的未知量与情境是否相符.
教学反思:通过案例分析不难发现,这是一种探究、讨论、启发式的教学过程.在此过程中,教师一直引导鼓励学生自主探究、合作交流,培养自觉思考的良好习惯,实现对实际情境问题的数学建模.
4 驱动内化解题的潜能,强化学生对数学建模的解题应用
对实际问题的数学建模,其作用之一是规范学生的解题步骤,形成一种抽象思维的定式.因此,在课题的导入情境中作出相应的变式,让学生在已经熟悉的情境中拓展思维是很有必要的.也就是说,对一节课的知识要巩固,通过变式练习达成“堂堂清”[2].
变式情境(电子白板展示)如图1,Rt△ACB是一养鱼池的一角,∠C=90°,为了捕鱼,一渔网同时由A,B两点出发分别沿鱼池边缘AC,BC方向向点C匀速移动至点Q,P,渔网的速度分别是1.5 m/s,1 m/s,若△QCP的面积为Rt△ACB面积的一半,则需经过多长的时间?
教学案例2
生:不能直接设点A到点Q的距离或点B到点P的距离了,应该设需要的时间为xs,这样AQ=1.5xm,BP=xm,于是有CQ=(15-1.5x)m,CP=(10-x)m.
师:这两个数据都符合实际情况吗?
生:当点Q,P在Rt△ACB的边上时,15-1.5x>0且10-x>0,即0 教学反思:这个案例是最初导入情境的变式,尽管情境涵盖的数学关系式的原理是相同的,但比原来的问题情境有了进一步拓展,即不能直接设定点Q,P走过的路程了,除非学生发现了AB∥QP,这需要独到的眼光才能察觉.所以,在用一元二次方程解决实际问题时,假设的未知量也至关重要. 总之,用一元二次方程解决实际问题时,问题情境的表达方式是实际情境的真实反映.当其中有些数量关系比较隐蔽时,在探究过程中假设未知量以及正确建立一元二次方程是学生的难点,需要教师恰当地引导.在课堂教学过程中教师要做到:创设现实生活中的实际问题情境,引导学生进入课题;引导探究解题过程,帮助学生对实际问题进行数学建模;驱动内化解题的潜能,强化学生对数学建模的解题应用.这样,就一定能够让学生弄清问题情境,锁定已知,构建联系,设定未知,发展思维.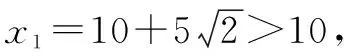
5 结束语

