学材再建构 促进学生深度学习
⦿江苏省海安市城南实验中学 周 澜
1 引言
一般来说,学材不仅仅包含教材还包含供学生学习的各种材料或者资源.学生的学习、体验、拓展、运用等都离不开学材.学材再建构是以学生为中心的重要理念,是让学生得到适切提升的重要方式.教学中教师可依据学生的最近发展区,以他们当前的迫切需要为出发点,以实现学习实效最大化为目的,对各种学材进行统筹安排,或增删、或调序、或拓展,进而打造最适切的教育[1].
2 学材再建构,注重相关认知的体系建构
学生在解决数学问题的时候经常会出现这样的现象,在教师的指导下能顺利地完成某一题目的解答,但是当遇到类似题目的时候,却解答不出来.这说明学生还没有形成举一反三的能力,还没能建立起相关认知的体系结构.这就需要教师对具体的题目进行学材再建构,以让学生悟出这一类型题目的特征,以及解决的方式,进而建立相关的知识脉络.
以人教版初中数学八年级下册“勾股定理”为例,就勾股定理的运用,教材上呈现这样的例题:一个门框的尺寸如图1所示,一块长3 m,宽2.2 m的薄木板能否从门框内通过?为什么?
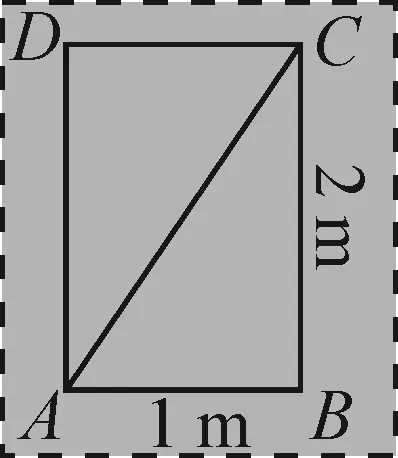
图1

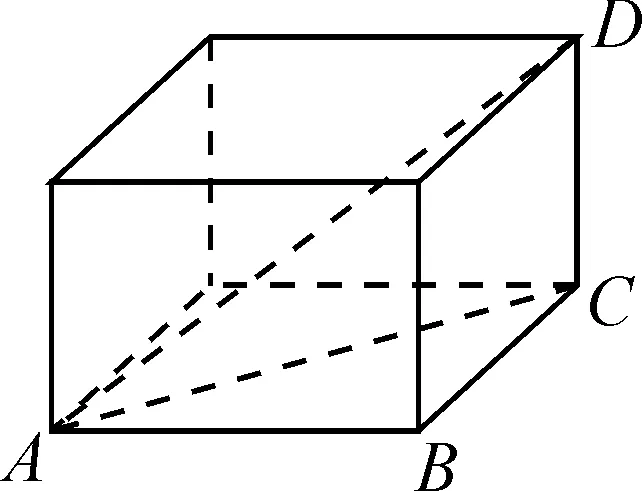
图2
3 学材再建构,促进深度学习的真实发生
当前,在数学教学中经常会出现这样的现象,教师不能满足学生的需求进行学材再建构,以促进他们深度学习的发生.深度学习是促进学生高阶思维的需要,也是提升核心素养的需要.教学中教师要依据学生的认知,以及学习时的情感态度,对学材再建构,以让深度学习在课堂发生.
还以人教版初中数学八年级下册“勾股定理”为例,教材中展示了中国古代数学家赵爽证明勾股定理的方法.学生自然想到有没有别的有趣的证明方法,思维顺着勾股定理的证明发散开来,这是深度学习的表征.相应地,教师建构这样的学材:美国第20届总统加菲尔德证明了勾股定理,大家想不想尝试.
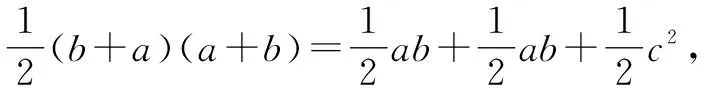

图3
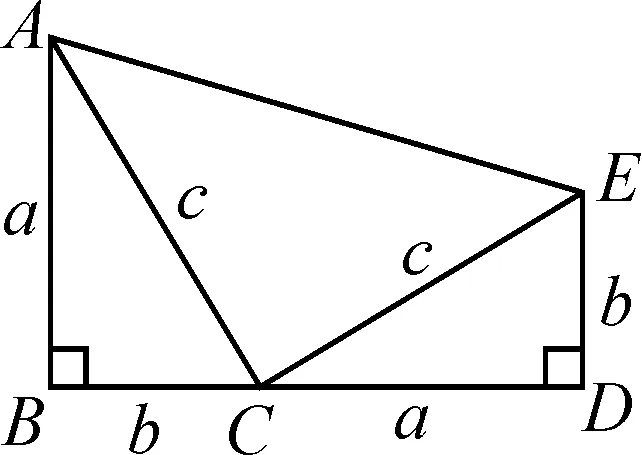
图4
4 学材再建构,提高学生学习的主观能动性
学材再建构能调动学生的学习兴趣,激发他们的主观能动性.教师可以依据学生的思维特点以及情感需要,建构他们喜欢的学材,进而让他们以积极主动的姿态,开展数学探究活动[2].
学生从课本的“赵爽弦图”感知到古人的智慧,同时也对古代的数学产生了好奇.教师顺势建构这样的学材,《九章算术》中有一题:今有竹高一丈,末折抵地,去根三尺,问折者高几何?学生先是饶有兴趣地去弄懂文言文的含义,通过小组讨论,发现原题可以这样表述:有一根竹子原高1丈(1丈=10尺), 中部有一处折断,竹梢触地面处离竹根3尺,请问折断处离地面多高?
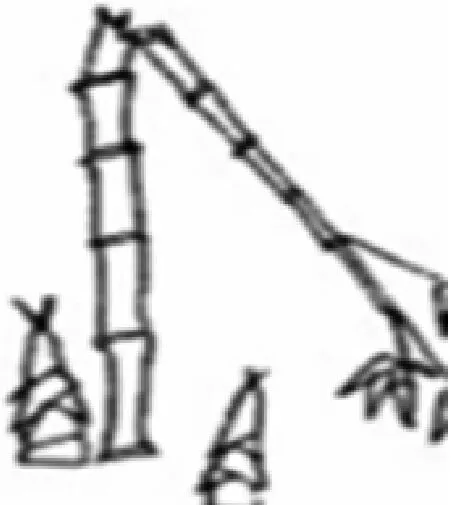
图5

图6
学生先是将原题转为图5的简笔画,将题目要表达的意思进一步明朗化.教师问能不能将图5进一步转化为数学图形,与今天的所学的知识对照.学生画出图6,用线段OA和AB表示竹子,用线段AB表示竹子折断部分,再用线段OB表示竹稍触地处离竹根的距离.这样的图建构好之后,依据题目的含义,设OA=x,则AB=10-x,再利用勾股定理得出最后的结论.显然,这样的学材再建构既开阔了学生的视野,又激发了探究的热情.提升学生的主观能动性,使其成为学习的主人,学材再建构是重要的路径.它引发学生思维自主地往纵深发展,进而落实学科素养的培育.因此在教学中,教师要基于学材再建构组织教学,给学生鲜活的学习材料,适宜的生长土壤,使他们成为学材再建构的主动参与者,同时也让“学材”发挥最大的效益.
5 结束语
总之,学材再建构能让教师更好地提升学生的思维能力,减轻他们的学业负担.同时,学材再建构也能让学生获得更系统化、结构化的认知,进而促进他们的深度学习.

