一元一次不等式组中参数取值范围的确定方法
⦿白银区武川新村学校 刘振琴
1 引言
含参数的一元一次不等式组中参数取值范围的确定是“一元一次不等组”这一节的重难点内容.从课堂教学情况来看,学生在该知识点上存在很大问题,出现了诸多错误.所以,笔者对一元一次不等式组中参数取值范围的确定方法进行了研究,希望对学生有更多帮助.
2 例题分析

分析:本题中的不等式组无需进一步求解,只需在数轴上将x
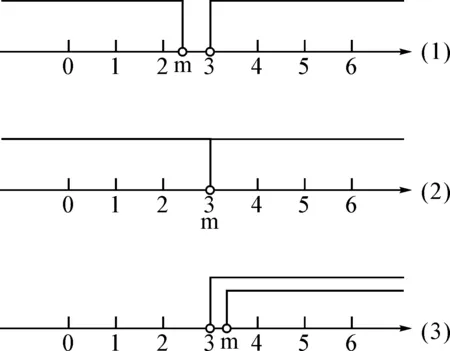
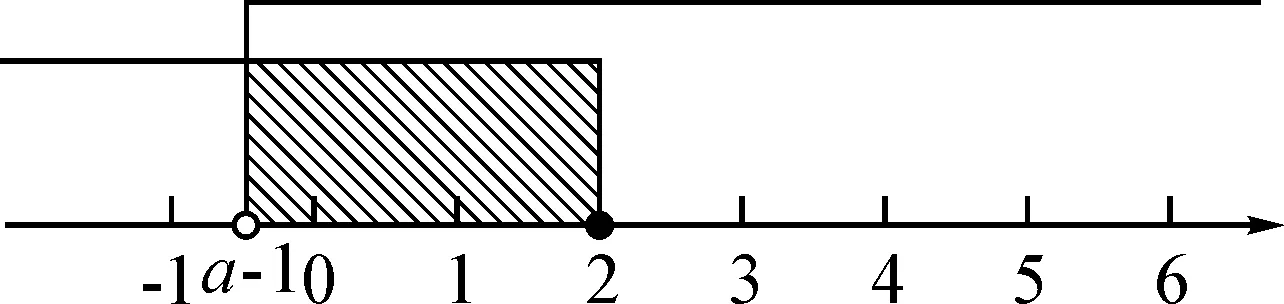
第一步,画出数轴,在数轴上表示出x>3的解集,将x 第二步,将x 第三步,观察符合题意的x 解:首先,将x 图1 然后,分析x 图2 再者,根据“无解”这一题意,可以确定(1)(2)两种情况符合.很明显,(1)中m<3,(2)中m=3. 最后,综上分析可得出m的取值范围为m≤3. 分析:本题与例1的不同点在于本题中不等式组需要求解及不等式组有解集两个方面,同样用数形结合和分类讨论的方法分析如下. 第一步,解出不等式的解集,分别是x>a-1和x≤2; 第二步,画出数轴,在数轴上表示出x≤2的解集,将x>a-1的解集表示图如图3所示画出; 第三步,将x>a-1的解集表示图在数轴上移动,直至找出符合题意的情况; 第四步,观察符合题意情况下的x>a-1解集表示图所在的位置,比较a-1与2的大小. 将不等式组的解集在数轴上表示,如图3所示: 图3 因为原不等式组有3个整数解,所以a-1一定小于2.因为x≤2确定了原不等式组中的一个解,又由于x>a-1,a-1处是空心,所以在满足原不等式组有三个解的前提下,a-1一定要在0的左边、-1的右边,即-1≤a-1<0,如图4所示. 图4 所以,a的取值范围是0≤a<1. 通过以上两道例题的分析可以发现,一元一次不等式组中参数取值范围的确定,不仅要利用数形结合的方法将之直观地在数轴上表示出来,还需要借助分类讨论思想,对符合题意的几种情况逐个分析[1].对于这类问题,大致可采用以下思路解决: 第一步,解.解出不等式的解集. 第二步,画.画出数轴,在数轴上分别表示出不等式组的解集.对于含参数的解集,可像例1,2中一样先画出其形状待用. 第三步,移.将含参数的解集表示图在数轴上移动,直至找出符合题意的情况. 第四步,比.观察符合题意情况下含参数的解集表示图所在的位置,比较对应数字的大小[2]. 另外,在操作第三步和第四步时,需注意以下几个方面的问题: 首先,为了让学生有更直观的移动体验,教师可以利用多媒体画图工具,先用一种颜色将不含参数的解集在数轴上画好,然后用另一种颜色将含参数的解集在数轴以外的地方画好,然后利用“平移”或“移动”工具移动该解集的表示图,让学生经历解集表示图移动的过程,更直观地感受符合题意的几种情况.这样操作,比教师包办效果更好. 最后,解、画、移、比是解这类问题的通用步骤,学生不仅要对这些步骤进行常规化练习,而且要进行变式训练,以不断激发思维和拓展解题思路[4]. 综上所述,虽然含有参数的一元一次不等式组会给人以疑惑感,但如果能在“解”的基础上一步步尝试探究和深入,学生可能会获得不一样的学习心得.这种心得不仅体现在学习本身,更体现在与学生全面发展有关的诸多素养方面.所以,作为一线教师不仅要重视解、画、移、比这四个步骤的不断训练,更要借助变式练习激发学生的思维,培养学生更好的学习品质,为学生更全面的发展奠定基础.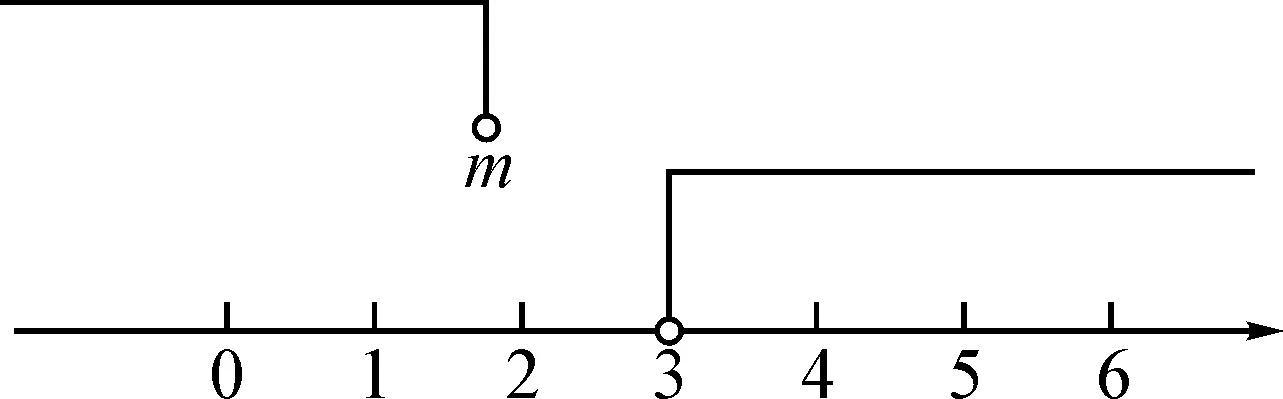
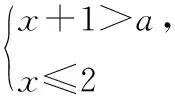


3 解法总结
4 结语

