基于非周期采样Takagi-Sugeno模糊系统的H ∞控制

沈宇凯夏建伟

(聊城大学 数学科学学院，山东 聊城 252059)

0 引言

近些年来，Takagi-Sugeno(T-S)模糊系统受到学者们的广泛关注与研究，因其在描述复杂非线性系统问题时成效显著。T-S模糊模型以线性子系统加权和的形式将非线性系统转化为理论相对完备的线性系统，借已有分析方法与控制技术之利刃解决现有问题。迄今为止，人们围绕T-S模糊系统进行的研究，正枝繁叶茂且硕果累累，如自适应控制[1]、保成本控制[2]、状态估计问题[3]等。T-S模糊模型也已在许多动态系统中得到应用，如网络控制系统、交换系统、随机系统等[4-6]。因此，植根于模糊系统的研究仍生机蓬勃，许多问题仍亟待解决。

同时，随着数字技术的快速发展，采样控制的研究也得到高度重视。该控制方法只需利用系统状态的瞬时采样信息，因而极大减少了信息传输，故在能保证系统更好性能的同时能降低系统运行成本。采样控制给我们的生活带来了诸多便利，相关的研究方法也纷至沓来，如输入延迟方法[7]、离散时间系统方法[8]及闭环函数方法[9]等。在实际控制中，周期采样虽简单可行，但是诸如外部环境的变化会影响周期采样过程，非周期采样的实现就显得尤为重要。在事件触发和网络化控制系统中，由于传输信道中可能会出现丢包、拥塞等情况，或是为了降低信道使用率及通信成本，仅以不满足给定阈值的触发状态作为控制器输入时，均将使得传输给控制器的输入无法进行周期性采样。以实际应用角度看来，当系统的运行轨迹比较平坦时，可以采用与状态轨迹剧烈抖动时不同的采样频率，即选择较大的采样周期更为合理。因此，非周期采样是一种比周期采样更普遍、更实用的反馈形式，对其研究具有重要的理论意义和实用价值。在周期及非周期采样控制中，如何有效增大采样周期是其重中之重，这方面的研究也有一些比较有意义的结果，例如，ZENG 等人[10]通过构造充分利用系统信息的李雅普诺夫函数、改进积分不等式，有效地增大了系统采样周期；WU 等人[11]通过李雅普诺夫方法，设计了期望的采样状态反馈控制器，有效地提升了系统性能。

另外，为了在保证系统性能前提下实现稳定，学者们研究了H2控制、H∞控制等多种方法来合成控制器。特别是H∞控制，能有效地抑制系统扰动，它已在各种实际系统中进行了研究，如电动地面车辆、电动列车的异步电动机控制问题[11-15]。基于上述分析，便启发了我们本文的研究。

本文基于非周期采样控制，研究了T-S模糊系统的H∞性能分析问题。创新之处在于:(1)构造了一个由双边闭环函数组成的李雅普诺夫泛函，该泛函能充分利用系统信息，极大地扩大了采样周期，降低了主要结果的保守性；(2)在稳定性条件基础上，设计了相关控制器，使系统在满足H∞性能条件下，能使系统保持稳定。

1 系统描述

考虑具有连续时间的T-S模糊系统，IF-THEN 规则描述如下

(1)规则i:IFφ1(t)isζi1 ，φ2(t)isζi2 ，…，φp(t)isζip，THEN

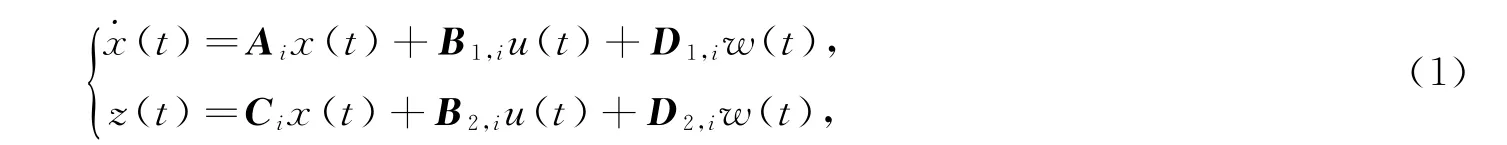
式中i∈R＝{1，2，…，r}，r是IF-THEN 规则的数量，φ1(t)，φ2(t)，…，φp(t)是前提变量，ζi1，ζi2，…，ζip是模糊集合。x(t)为系统状态，u(t)为控制输入，w(t)是在L2[0 ，＋∞) 上的干扰输入，z(t)∈R s是控制输出。

基于模糊推理方法，系统(1)可重构为

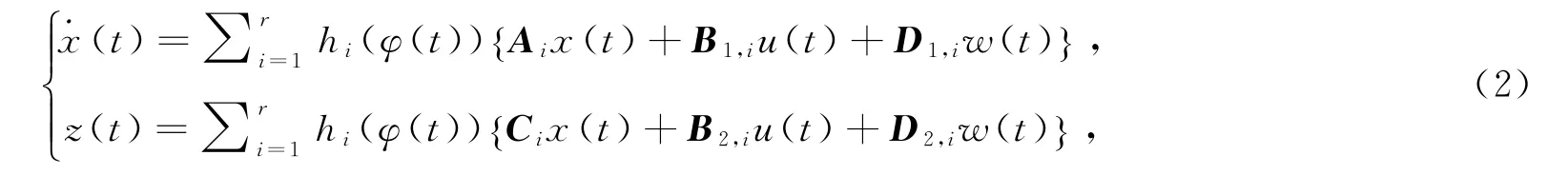
式中φ(t)＝[φ1(t)，φ2(t)，… ，φp(t)]，并且

ζiκ(φκ(t)) 是φκ(t)在ζiκ(κ＝1，2，…，p) 上的隶属度。我们可以知道，对于所有的t，，并且。然后，将得到的模糊系统模型作为该形式局部模型的加权平均值进行推导，我们有

(2)规则j:IFφ1(t)isζj1 ，φ2(t)isζj2 ，…，φp(t)isζjp，THENu(t)＝K j x t k( ) ，j＝1，2，…，r。基于模糊推理方法，上式可重构为u(t)＝K(t)x t(k) ，其中

将上述控制器代入(3)可得闭环系统

定义在零初始条件下，存在满足每一个非零向量w(t)∈L2[0 ，∞) 的控制律，系统(4)在H∞范数γ＞0有界条件下是稳定的，其控制输出满足以下不等式

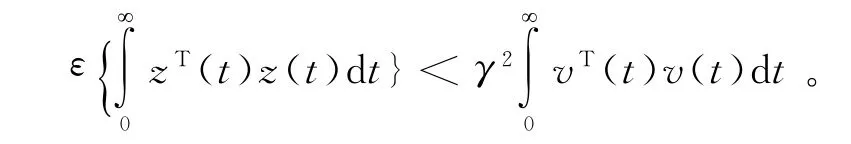
2 主要结果

在这一部分中，我们将获得解决上一节所描述的问题的一个充分条件。现在，我们考虑以下系统

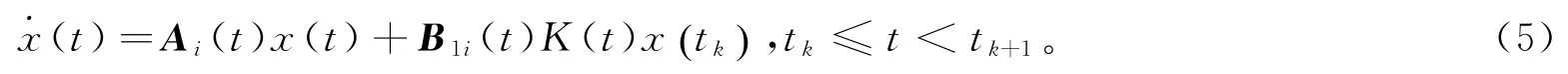
当控制器为常数时，给出下列稳定性条件。

定理1系统(5)是稳定的，若存在矩阵P＞0，H1＝HT1，H2，H3＝HT3，H4及具有相应维数的任意矩阵G1，G2，G3，对于任意的h k∈[h m，h M] 满足下列线性矩阵不等式

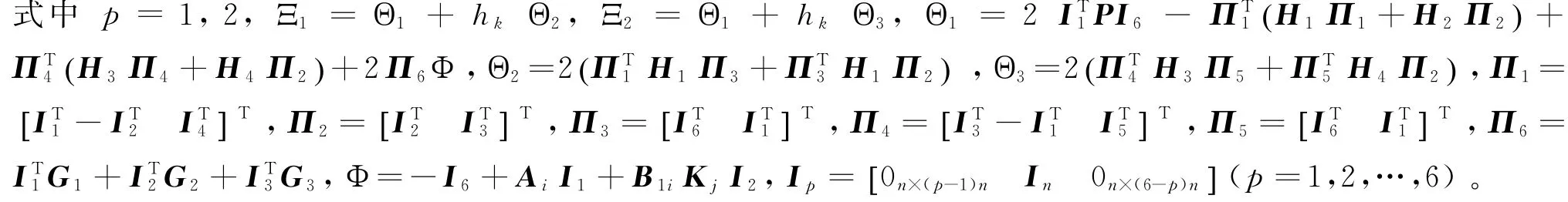
证明让我们考虑以下李雅普诺夫函数

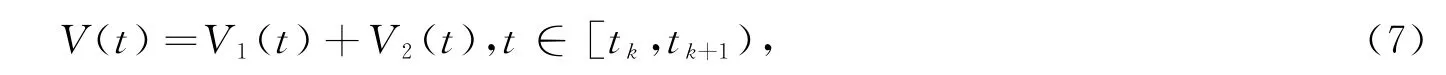
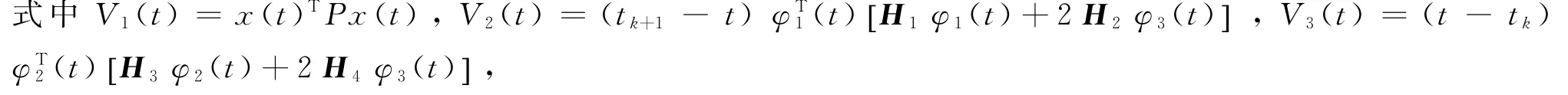
对上述李雅普诺夫函数(7)沿着方程组(5)的解求导得到

另一方面，根据系统(5)，对相应维数的任意矩阵G1，G2和G3，满足以下零等式

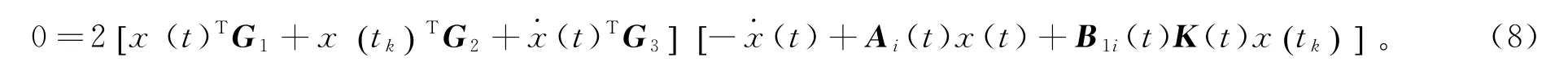
将(8)式的右端加到˙V(t)上去，对于t∈[t k，t k＋1)，我们得到

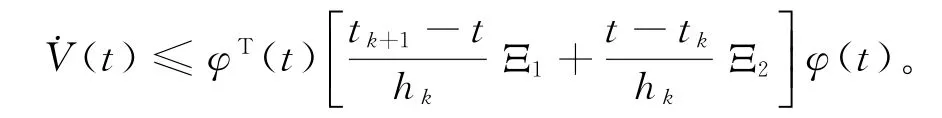
利用公式(6)，我们得到˙V(t)＜0。

因此，由稳定性定义可知，系统(5)是稳定的。

注1值得指出的是，我们在这里构造的李雅普诺夫函数V(t)由双边闭环函数组成。该函数充分考虑了区间[x(t k)x(t)] 和[x(t)x(t k＋1)] 上信息。注意V q(t k)＝V q(t k＋1)＝0，q＝2，3，因此V q(t)满足闭环函数条件。然而文献[15]中所构造的李雅普诺夫函数仅包含了信息，不包含信息，而我们构造的函数V(t)将两者都包含在内。因此，本文推导的结果具有较小保守性。

基于定理1，我们可以得到系统(4)在H∞范数有界条件下的稳定性定理。

定理2对于一个给定正标量γ，系统(4)在H∞范数有界条件下是稳定的，若存在矩阵P＞0，H1＝HT1，H2，H3＝HT3，H4及具有相应维数的任意矩阵G1，G2，G3，对于任意的h k∈h m，h M[ ] 满足下列线性矩阵不等式

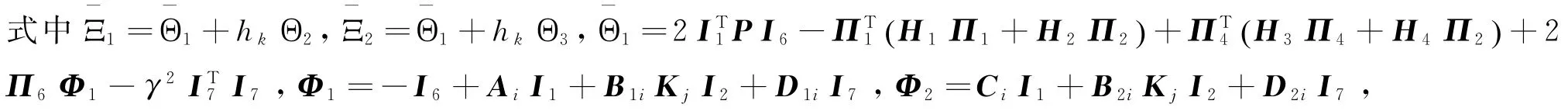
证明根据定理1，当w(t)＝0时，系统(4)是稳定的。接下来，我们将证明系统(4)在H∞范数有界条件下是稳定的。定义

类似于定理1的证明过程，对任意t∈[t k，t k＋1)，我们可以得到

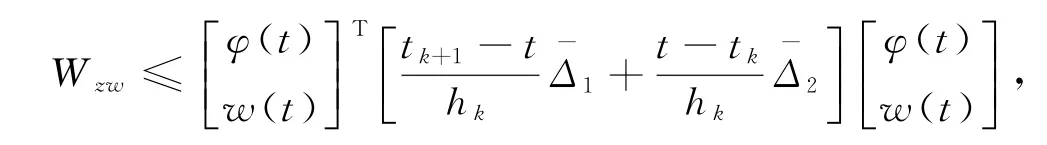
根据舒尔补引理，由式(9)，我们有

因此，对于任意τ≥0，存在一个整数α≥0满足tα≤τ≤tα＋1。我们可以由式(10)和式(11)得到

根据定理1的证明，可以得到V(t k)＝V(t－k)。故，对于零初始条件，我们有

所以，根据定义可以看出，系统(4)在H∞范数有界条件下稳定。

基于定理2，下面给出相应状态反馈采样控制器。

定理3对于一个给定正标量γ，系统(4)在H∞范数有界条件下是稳定的，若存在矩阵及具有相应维数的任意矩阵，对于任意的h k∈[h m，h M] 满足下列线性矩阵不等式

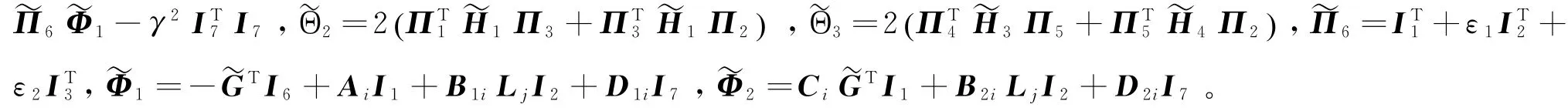
在这种情况下，给出以下所需控制器增益

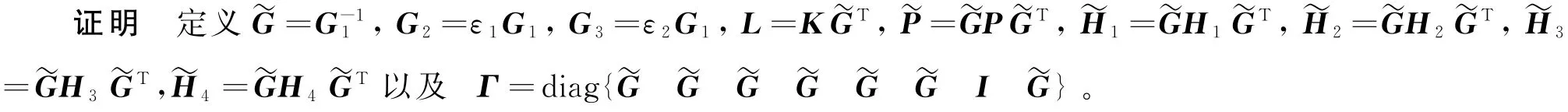
在式(9)的左边和右边分别乘以Γ和ΓT，我们可以得到式(12)。

3 仿真算例

在这一节中，我们提供了一个例子来证明本文所提出方法的有效性。

例1让我们考虑以下卡车-拖车模型

式中x1(t)表示卡车和拖车之间的角度差，x2(t)表示拖车的角度，x3(t)表示拖车尾部的垂直位置，w1(t)和w2(t)表示干扰输入，模型参数

并且h2(Θ(t))＝1－h1(Θ(t))，其中10－2/π。

上述非线性系统的T-S模糊模型描述如

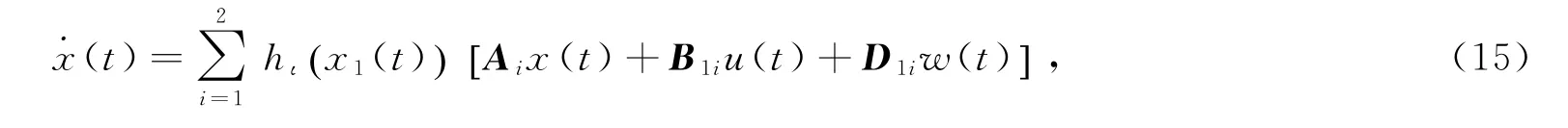
式中

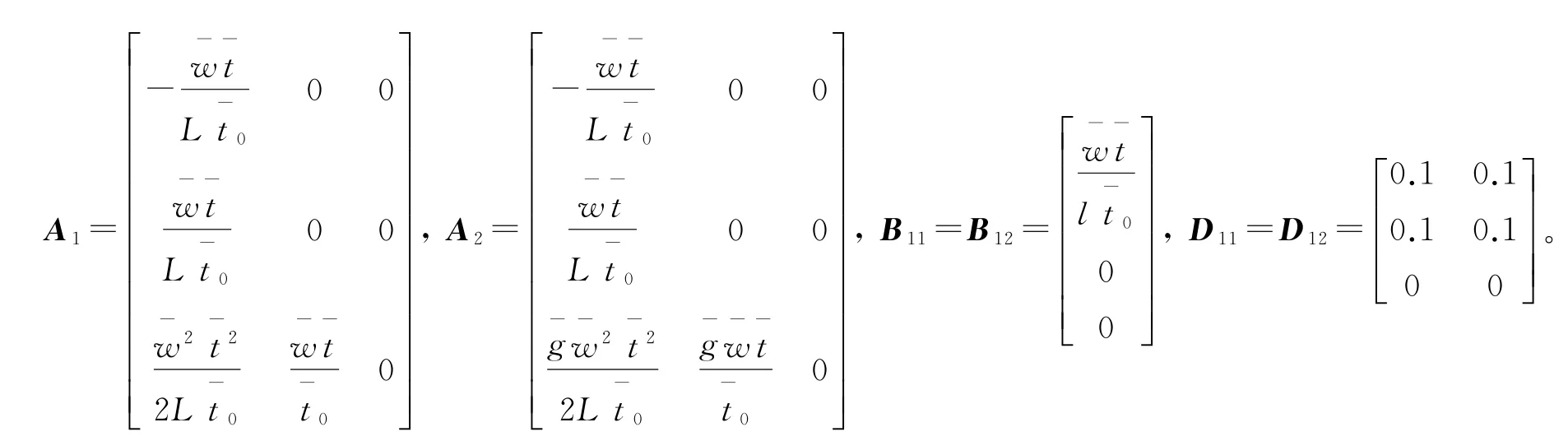
控制器输出z(t)选择如下参数

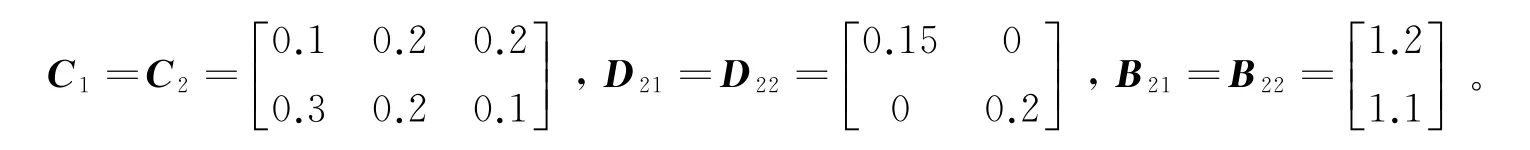
首先，考虑采样周期不确定的情况。基于定理3在ε1＝ε2＝0.5且h m ＝0时，表1给出了H∞性能γmin对不同采样周期的上界。

表1 当h m ＝0时,不同h M 所对应的性能指数γmin

接下来分析确定采样周期的情况，即h m ＝h M ＝h。

从表2中我们可以看出，当采样周期增大时，所对应的H∞性能指数也是随之增大的。换句话说，我们可以通过增加采样频次来提升系统的H∞性能。另外，我们选取γmin＝1.8，采样周期h m ＝0.1，h M ＝0.3时，求解定理3 我们可以得到如下控制器K1＝[7.6241－8.2589 1.3543]，K2＝[7.6128－8.0863 1.3863]。

表2 不同h 值所对应的性能指数γmin

基于上述控制器，选取系统的初始值x0＝[－0.5π －0.75π －6] ，我们可以得到系统的状态响应如图1所示，系统的输出响应如图2所示。

图1 系统的状态响应

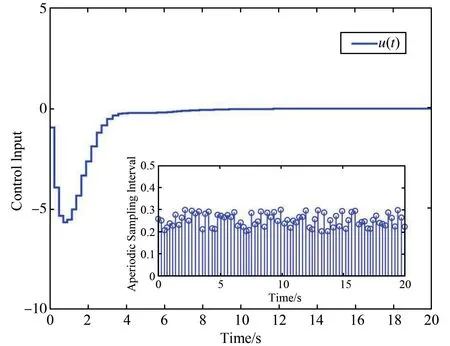
图2 系统的输出响应

从图1，图2我们可以看出，我们的方法行之有效。

例2考虑如下有两个模糊规则的系统[15]，参数如下

基于定理3，在不考虑时滞的情况下，我们可以得到当最大采样周期h M ＝0.30时，H∞性能指标γmin＝0.4160，而文献[15]中得到的H∞性能指标γmin＝0.9947；当我们取H∞性能指标γmin＝0.9947时，可得到最大采样周期h M ＝0.481，这比文献[14]中得到的结果提升60.33%。由此可见，本文得到的结果保守性更小。

4 结论

针对一类带有外部干扰的T-S模糊系统，本文构造了一种新的李雅普诺夫泛函，该泛函充分利用了系统信息，有效降低了实验结果的保守性。基于此泛函，本文提出了T-S模糊系统的稳定性条件，并设计了相关控制器，保证了系统在满足H∞性能条件下的系统稳定性问题。同时，仿真算例也说明了该方法的有效性。