磁悬浮径向轴承振荡电磁力控制仿真研究

赵青云，杨培林

(山西师范大学物理与信息工程学院，山西 临汾 041000)

1 引言

磁悬浮径向轴承利用其特有的电磁力，使物体悬浮于空中，最突出的特点就是转子的旋转过程与定子不接触，不会产生摩擦，可最大程度延长轴承的使用寿命。在航空、工业、轨道交通等领域起到了非常重要的作用。与常见的滚珠轴承有所区别的是，磁悬浮轴承的转子在运行状态下不接触传感器，而是直接悬浮于空中，极易受到振荡电磁力的影响，产生较大的振动，使转子偏离预先的位置。磁悬浮径向轴承在运行过程中存在振荡现象，会引发严重的安全事故，造成经济财产和人员伤亡，因此，需要对振荡电磁力进行有效控制。

参考以往研究内容，在各种控制方法中，由于磁悬浮轴承是一种强烈的非线性系统，很难实现对其进行精准建模，就此文献[1]深入研究转子与电磁铁之间的关系，并结合神经网络算法，寻找滑膜控制律；通过调整模型参数，控制误差权值，实现模型对转子的稳定性控制。但是该算法的模型参数需要反复测试才能得到合适的数值，过程较为繁琐；文献[2]则将分散PID与滤波交叉反馈法相结合，提出了一种数字化控制方法。通过对轴承中转子的特性进行深入分析，并以此构建了转子偏转动力学模型，实现对转子系统耦合特性的精准划分，引入PID控制器与滤波交叉反馈结合，消除模型中的陀螺效应；最后，构建数字控制系统，利用双线性变换实现对转子的稳定性控制。该方法有效克服了强陀螺效应对转子的稳定性影响，但是没有消除稳态误差的影响，不能满足精准度要求。

基于以上方法存在的问题，本文提出了一种高效的振荡电磁力自动控制方法。首先，对磁悬浮径向轴承的特性进行深入分析，确定电磁力的主要影响因素是电学系统和力学系统；利用模糊自整定PID控制器对一阶惯性环节的电磁力系统中三个参数实时调整，使值保持在合理范围内。通过与传统方法展开对比实验，结果验证了所提方法具有更为明显的优势，在有效控制振荡电磁力的同时保证了响应时间最快、超调量最小，具有非常优秀的静态/动态性能。

2 磁悬浮径向轴承特性分析

磁悬浮径向轴承的机械构成和控制系统非常复杂，属于高科技机电一体化产品，构成模块和实现过程如图1所示。

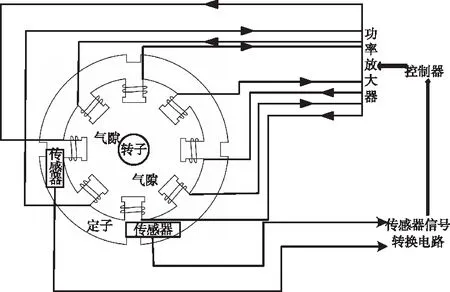
图1 磁悬浮径向轴承控制系统结构图

电磁铁产生的磁力对转子在运行状态下的稳定性会产生一定的影响，本文利用差动控制法实现转子的稳定悬浮。差动控制的基本原理主要分为两个部分：一是利用一个磁极对偏磁电流I0和控制电流i(t)进行相加运算，所得的和即为I0+i(t)；二是进行相减运算，所得的差即为I0-i(t)。在控制系统中功率放大器的作用下，调整电磁铁的电磁力大小，从而调节转子的悬浮点位置。

转子相对于电磁铁而言，自身刚度为无穷大，所以本文对研究过程中转子的形态变化和弹性振动忽略不计。将Φm1、Φm2定义为两个电磁铁的气隙磁通，F1、F2分别表示两个电磁铁产生的磁力大小，S表示电磁铁磁极所占的面积大小，μ0表示没有空气供应时电磁铁产生的磁导率，Ψ1、Ψ2分别表示两个电磁铁产生的磁链。

1)电磁力方程

在物理学理论的基础上，计算两个电磁铁的气隙磁通[3]

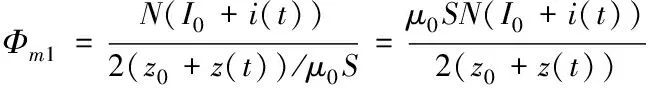
(1)

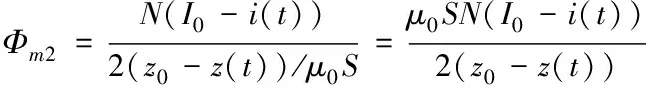
(2)

式中，N表示线圈的绕组匝数，z(t)表示转子与平衡位置之间的偏差程度，z0表示转子在指定悬浮点时的气隙。

电磁铁绕组产生的互感系数为

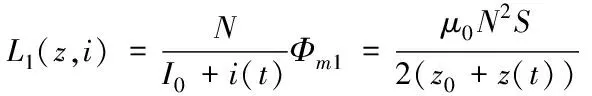
(3)

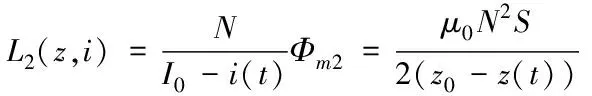
(4)

电磁铁绕组产生的瞬时电感为

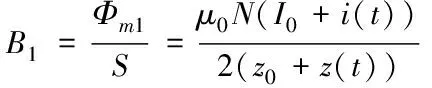
(5)

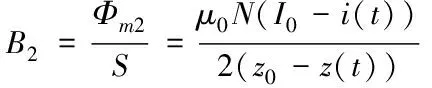
(6)

通过计算上式可以得出

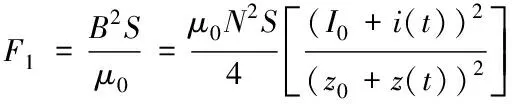
(7)

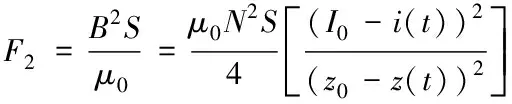
(8)

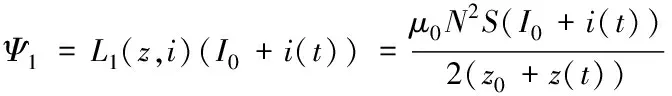
(9)

(10)

在某一时刻下，磁悬浮轴承所承受的电磁力F(z，i)为

F(z，i)=F1-F2

(11)

由式(11)可知，当i(t)≻I0时，只需要一个电磁铁产生磁力即可，此时可以计算得到最大回复力[4]，将式(11)进行转换可得到

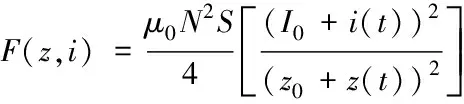
(12)

通过计算式(12)可知：电磁力F与电流I0+i(t)的平方呈正比例、与气隙z0+z(t)的平方呈反比例。由此可以得出结论，磁悬浮径向轴承属于一个非线性模型[5]。

2)电学方程

将R定义为绕组中的直流电阻，即可得到回路中的电压方程为

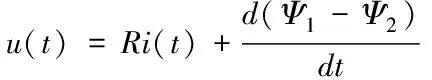
(13)

3)动力学方程

在径向轴承的方向上，电磁铁的动力学方程公式为

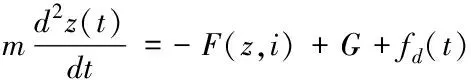
(14)

式中，fd(t)表示磁悬浮轴承在运行状态下所受的干扰力[6]，m表示转子的质量，G表示转子的重力。

通过式(15)即可计算得到磁悬浮轴承的数学模型为：

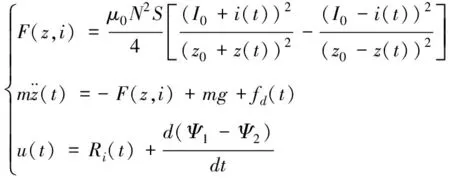
(15)

式中，u(t)表示磁悬浮轴承中的控制电压。

该数学模型由一组非线性方程组成，表示的是磁悬浮径向轴承的基本特性。

3 磁悬浮径向轴承振荡电磁力控制的实现

3.1 控制策略

通过上文对磁悬浮轴承的特性分析可知，磁悬浮轴承的电磁力系统主要由电学系统和力学系统构成。电学系统类似于一个一阶惯性环节，而力学系统中，电磁力F的大小由电流I0+i(t)和气隙z0+z(t)共同影响。在电磁铁中，由于线圈带有一定量的电感，所以电学系统的控制效率要远远小于力学系统的控制效率[7]。由于磁悬浮轴承数学模型为一个非线性方程，所得结果更接近于实际结果，而线性方程计算结果与实际结果相差较大，所以本文利用非线性方程组，控制电磁铁振荡，降低误差的影响。

由于磁悬浮轴承的特殊性，使其在运行状态下，气隙内不免进入其它杂质，产生不同程度的干扰影响。所以，本文在动力学理论的基础上，提出振荡电磁力控制策略。将力引入到控制器中，可以更加有效地处理外界干扰因素的影响，从而提高算法整体的稳定性和可靠性[8，9]。

磁悬浮径向轴承控制器的动态方程组如式(16)所示

(16)

利用拉普拉斯对式(16)进行变换，得到如式(17)所示的公式

mS2Δz(S)=-ΔF(S)+Fd(S)

(17)

控制策略状态方程为

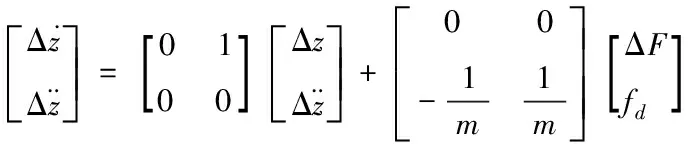
(18)

综上所述，磁悬浮轴承的传递函数为

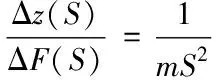
(19)

由此可得：磁悬浮径向轴承的特征方程式为

mS2=0

(20)

通过劳斯判据对式(20)进行分析可知：对振荡电磁力控制的过程属于二阶不稳定方程的计算过程，可以更好地控制系统中参数的变化，使其具有更强的兼容性。

3.2 模糊自整定PlD控制器结构

本文利用PID控制器(如图2所示)实现对振荡电磁力的自动控制。在电磁力系统内，输入误差e和误差变化率ec，在对其进行控制的过程中，通过e和ec实现对参数的自整定约束，并依照模糊准则，对参数进行合理的修改。

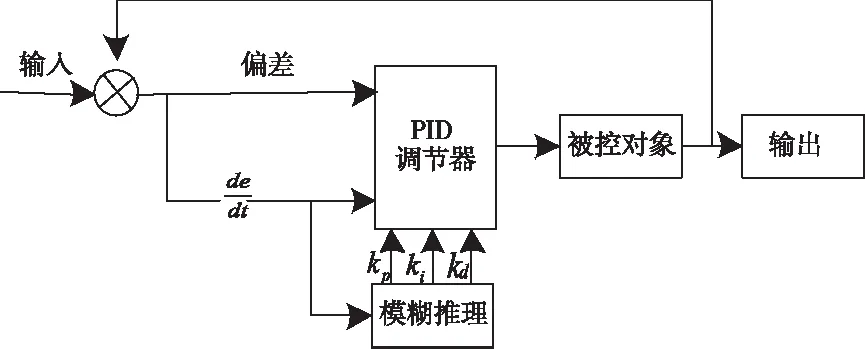
图2 模糊自整定PID控制器

PID控制器对参数进行自整定的过程，就是确定三个参数与e和ec之间关系的过程。在磁悬浮轴承运行状态下，通过模糊控制原理约束e和ec两个误差，实时调整三个参数的值，使其控制在合理的范围内，避免出现较大的振荡，保证磁悬浮径向轴承的静态/动态性能。

3.3 模糊自整定PID参数整定

综合考虑控制器的控制精度、稳定性以及其它方面的因素，对kp、ki和kd三者的作用和影响进行深入分析。

1)比例系数kp：kp的主要作用是使控制器具有理想的响应速度，同时保证控制器具有较高的控制精度。当kp的值较大时，控制器的响应速度也较快，控制精度也就越高，但是这种情况下极易出现超调现象，使磁悬浮轴承处于振荡运动状态下。当kp的值较小时，控制器的精度[10]也会相应降低，响应速度也较为缓慢[11]，降低控制效率，破坏控制器的动态/静态特性。

2)积分作用系数ki：ki的主要功能是检测[12]控制器中存在的误差并进行有效消除。当ki的值较大时，控制器的误差消除效率随之加快，当ki的值过大时，控制器在某一阶段就会出现过度饱和的情况，使得控制器出现较为严重的超调。当ki的值较小时，很难实现在较短的时间内消除掉控制器内的误差，使轴承转子偏离原始点位，产生较大的偏差。

3)微分作用系数kd：kd的主要作用是提高控制器的动态性能，确保电磁力在运行过程中不会产生较大的偏差，提前感知偏差并进行预防。当kd的值较大时，控制器提前被动响应，此时外界干扰对控制精度影响较大。

PID控制器在模糊规则的约束下，对e和ec进行模糊推理，并依照模糊矩阵表中所示的内容，对控制器参数进行合理的自整定修改。

4 仿真研究

为了验证本文方法在磁悬浮径向轴承振动电磁力自动控制方面是否有效，与上述所提文献神经网络和滤波交叉反馈进行了对比实验。实验在MATLAB仿真软件上实现，磁悬浮径向轴承的参数设定如表1所示。

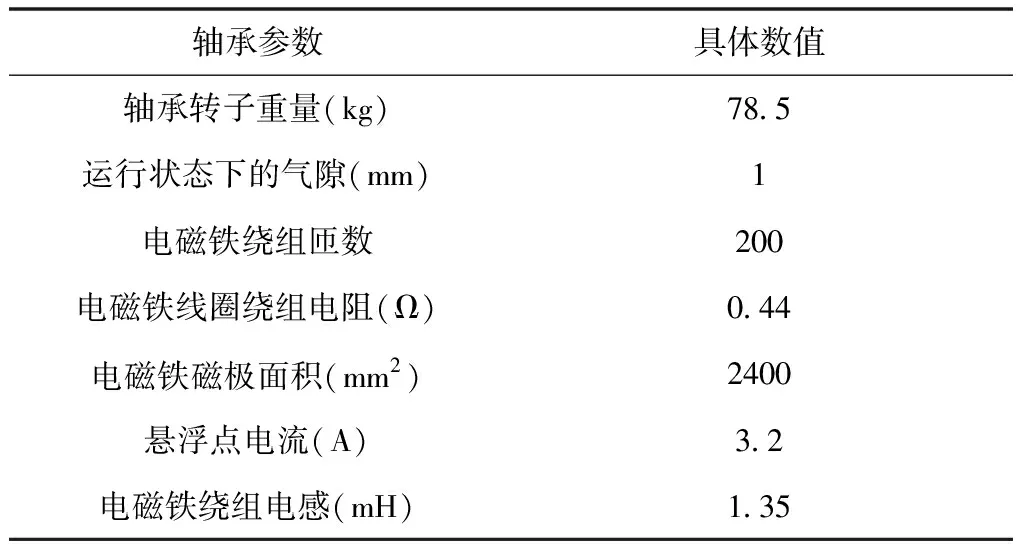
表1 磁悬浮径向轴承参数设定

对三种方法的振荡电磁力控制性能进行测试，实验环境为：从0s开始，气隙从初始位置移动到指定悬浮点1mm处，经过一段时间的振荡和调整，轴承逐渐进入工作状态。对三种方法在这个过程中产生的振荡电磁力控制进行性能测试，结果如图3所示。

图3 三种方法对于振荡电磁力的控制结果

从图3中可以看出，运用神经网络对振荡电磁力进行控制，从响应开始到气隙移动到悬浮点的时间大约为0.18s，而且可以很明显地看出振荡现象较为严重；滤波交叉反馈算法的响应时间较神经网络还要长，约为0.24s，振荡现象同样较为严重；而本文方法仅仅用了约0.08s就完成了位移，整个过程没有明显的振荡曲线，使磁悬浮轴承处于相对稳定的运行状态下。综上所述，本文方法在控制振荡电磁力方面性能最优。

接下来调整悬浮点的位置，从0s开始，经过0.5s的运行后，由原先的1mm突变为1.5mm，再经过0.5s后，悬浮点再突降为原先的1mm。测试三种方法是否能够稳定地控制振荡电磁力。图4为悬浮点突变时的气隙响应图，图5为控制振荡电磁力时电流变化曲线。

图4 悬浮点突变时气隙响应图

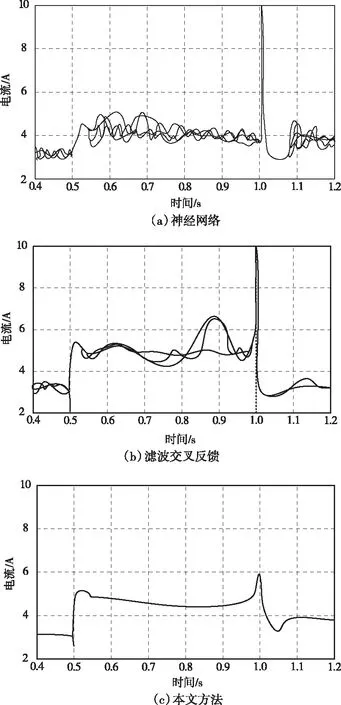
图5 振荡电磁力控制时电流变化曲线

从图5中可以看出，神经网络算法在控制过程中存在较大的超调量，电流振荡现象较为明显；滤波交叉反馈算法超调量有所减少，变化曲线较神经网络相比趋于平缓，振荡现象有所缓解；本文方法具有较小的超调量，并且电流没有出现明显的振荡现象，较其它两种方法相比性能最优。这是由于本文方法实时调整kp、ki、kd的值，使其在任意时刻下都满足磁悬浮轴承稳定性的要求。

5 结论

由于传统方法无法实现对磁悬浮径向轴承振荡电磁力的有效控制，常常存在控制偏差较大、响应效率过低等问题，为此，本文深入分析磁悬浮轴承特性，利用模糊自整定PID控制器，

修正传统方法中存在的缺点，提出了一种高效的自动控制方案。通过模糊自整定PID控制器对比例系数、积分作用系数、微分作用系数进行实时调整，防止其在运行过程中偏离原始位置，影响轴承的正常工作。在仿真中，也验证了本文方法具有较高的控制精度和较低的响应时间，总结如下：

1)模糊自整定PID控制器，使所提方法能够适应实际的磁悬浮轴承工作需要；

2)在动力学理论的基础上，将力引入到算法中，提高了算法整体的抗干扰能力。