星载陀螺数据的无阈值选用方法

毕成 于萍

(1 航天东方红卫星有限公司, 北京 100094)(2 北京控制工程研究所, 北京 100094)

陀螺是卫星姿态确定功能的重要部件，往往通过冗余配置来确保可靠性。长期以来，陀螺的选用方法，等价于陀螺的故障检测方法。如采用监测光纤陀螺的光功率[1]等物理量遥测来判断陀螺是否发生故障；采用平衡方程法[2]对冗余配置陀螺进行故障检测；利用其它敏感器的输出，进行滤波处理[3-6]评估残差来判断故障；和不依赖模型的信号处理方法[7-8]等。这些方法都需要设定合理阈值才能正确运行。

正常情况下，陀螺零偏可以通过地面或在轨标定进行补偿，其残差比较小。当按照陀螺噪声选取阈值时，只能在陀螺零偏较大变化时才能触发故障判据，不利于选择最佳的陀螺数据参与系统运算。

本文提出一种无阈值陀螺选用方法，综合平衡方程与星敏感器滤波，优选最佳陀螺组合。不仅可以去除较大故障陀螺(卡死、饱和等)，也可以在陀螺零偏缓变时选出性能最佳的陀螺组合。不仅适用于5个及以上的陀螺选取问题，也适用于4个陀螺的欠冗余选取问题。本文提出的方法可有效选取性能最佳的陀螺组合，能够有效提升卫星系统定姿精度；由于适用于陀螺的欠冗余选取，对于减少卫星系统陀螺配置，提升卫星系统的自主诊断能力具有积极意义。

1 平衡方程法

平衡方程[2]是工程上常用的陀螺故障检测方法。当有4个陀螺时(用下标i、j、m、l表示陀螺编号)，理想情况下它们的输出必然满足

(1)

式中：G*(下标*为陀螺编号)表示陀螺的安装矢量(列向量)；ω*表示陀螺输出的理想数据(不含误差)。当考虑到陀螺测量误差时，会有

(2)

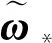
平衡方程具有非常好的工程应用经验，但当只有4个陀螺时，因只有1个平衡方程，无法通过平衡方程确定故障陀螺。这种情况对于陀螺诊断来说，属于欠冗余问题。欠冗余情况下，平衡方程诊断不再适用，需要开发新的方法选择可用陀螺。

此外，平衡方程法阈值受陀螺噪声影响较大，对于光纤陀螺、激光陀螺等噪声较大但零偏稳定性较好的惯性测量敏感器来说，为保证正常工作的噪声不误触发故障诊断，往往阈值需要设置较大，就很难诊断出不明显的缓变故障。

综上，为进一步适应陀螺数量少于5个的情形，并进一步提升陀螺组合性能优选的自主能力，有必要开发新算法。

2 基于星敏感器的无阈值陀螺选用方法

2.1 陀螺与星敏感器的误差模型

陀螺用于测量卫星的角速度。理想情况下，陀螺的输出表征特定方向的星体角速度，但实际陀螺输出都含有误差。陀螺的误差源主要包括常值零偏b*、测量噪声(即角度随机游走)nG*、刻度因子误差KG*、安装误差Kma*等[2，9]，其中KG*和Kma*是与星体角速度线性相关的。当发生故障时，可能是这几项误差的缓慢或突变。本文将这些误差项的非预期项，包含地面标定残差和在轨环境变化(含故障)引发的误差以f*表示。

nG*+f*

(3)

ωb表征星体实际角速度。将可标定误差项的和记为dω*后，陀螺误差模型可简化为

(4)

星敏感器误差模型：星敏感器误差[10]主要包括偏置、视场空间误差、像素空间误差、时域误差、热弹性变形误差、光行差等。其中偏置和光行差可通过校正基本消除，像素空间误差、时域误差表现为时域高频白噪声，而视场空间误差表现为时域低频有色噪声，热弹性变形误差为时域低频非随机误差。低频误差项的综合效果为数个角秒量级的误差，而高频误差项表现为白噪声，可以通过滤波进行抑制。

因此，可以将星敏感器的测量模型写为

qs=A(qvL)A(qvH)q

(5)

矩阵A为四元数乘法矩阵

(6)

式中：qs为星敏感器测量输出的四元数；q为理想测量值的星敏感器四元数；qvL为低频误差项和qvH为高频误差项[10]。

2.2 无阈值陀螺选用方法

本文提出的无阈值陀螺选用方法为2层结构，第1层为平衡方程检测，确定是否有显著的陀螺故障发生；第2层首先进行星敏感器比对，确认星敏感器数据的可用性，然后用滤波器依据星体运动学进行各个陀螺的零偏估计。当陀螺数量大于4个时，第1层检测出有陀螺故障发生时，剔除故障陀螺后选用残差最小的3个陀螺；当陀螺为4个的欠冗余情况时，由于平衡方程无法检测出故障陀螺，直接选用残差最小的3个陀螺。由于使用相对大小为检测原则，实现了无阈值的故障检测；方法的具体流程详见图1。

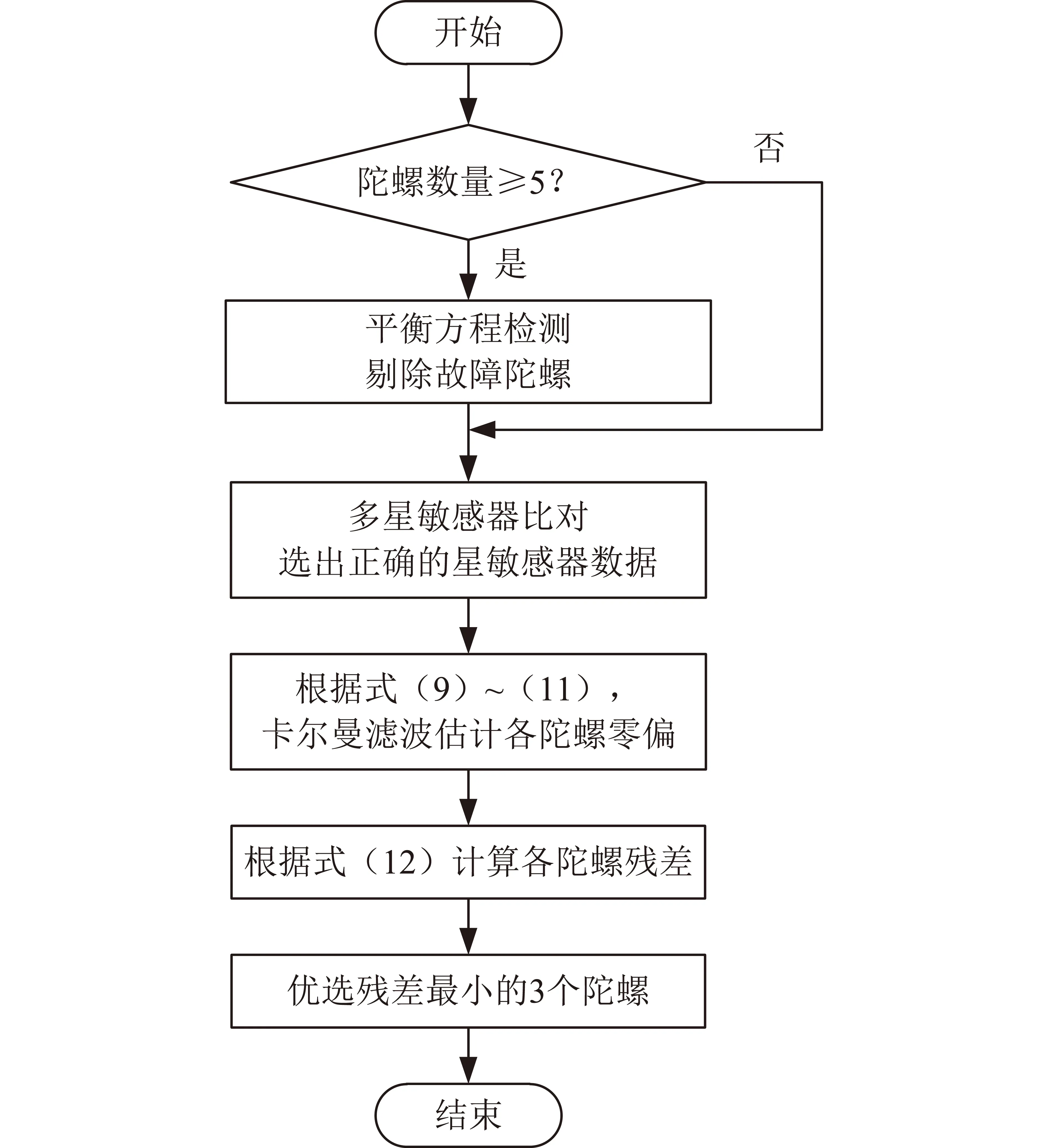
图1 无阈值陀螺选用方法流程图

1)陀螺零偏残差计算

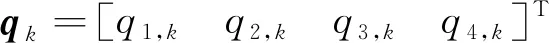
(7)

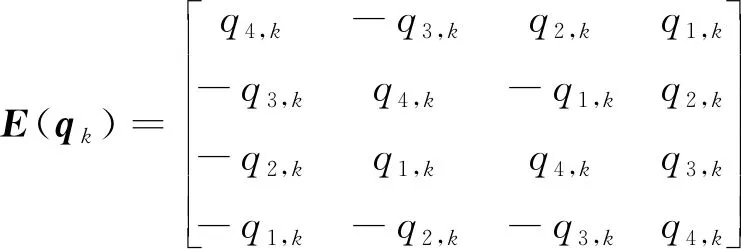
(8)

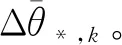
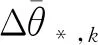
(9)

而陀螺零偏的状态方程与观测方程分别满足式(7)和(8)。

b*,k=b*,k

(10)

(11)

接下来使用残差进行陀螺选取，残差定义如下所示(陀螺零偏的初始装订值b0*)

(12)

注：由于滤波中使用星敏感器信息，星敏感器的输出正确性就尤为重要了。一般卫星上出于可靠性或寿命要求，都会安装多个星敏感器。在进行陀螺诊断前，可以通过多星敏感器数据比对来确定星敏感器数据的正确性。多星敏感器数据比对的基本思路就是将多个星敏感器的输出数据换算到同一坐标系下，通过容差比对，确认输出有效无异常，本文不做展开介绍。

2)陀螺选取

在满足平衡方程的陀螺中，优选r*,k最小的3个陀螺参与系统定姿运算。

3 验证情况

为说明方法的有效性，以装配有4个陀螺的情况为例，对不同故障情况、计算周期进行仿真。

设：4个陀螺中x、y、z三个陀螺正交并与卫星姿态本体坐标系平行，s陀螺斜装与本体坐标系三轴夹角均为54.73°。陀螺零偏标定后残差分别为0.03(°)/h、-0.02(°)/h、0.02(°)/h和-0.01(°)/h，陀螺的随机游走为0.005(°)/h1/2。星敏感器高频噪声3″(3σ)，低频噪声为幅值10″(3σ)周期2 h的正弦形式，星敏感器测量由式(5)产生。

1)例1

卫星工作在y轴角速度0.05(°)/s，在7200 s时z陀螺零偏突然增大到0.04(°)/h。该仿真用例说明了本文方法可以在4个陀螺且平衡方程无法诊断故障时，正确选择最优陀螺组。图2给出了不同计算周期时，陀螺残差的时间曲线及陀螺选取结果；其中标号234表示选用yzs陀螺，标号124表示选择xys陀螺。可以看出，随着故障发生后的时间增长，依据残差能够选出最佳陀螺组。图3给出了不同计算周期时，平衡方程的计算情况。

图3 陀螺平衡方程时间曲线

可以看出：随着计算周期的增加，由于数据统计效应，陀螺噪声减小；z陀螺零偏变化前后，噪声特性无明显变化，无法用平衡方程法诊断出有陀螺特性发生了变化。需要说明的是：在系统运行初始时段，因估值滤波需要时间才能收敛，应在系统滤波较为稳定后再根据估值情况选择陀螺。

2)例2

设卫星工作在y轴角速度0.05 (°)/s，在7200 s时z陀螺零偏突然增大到0.3 (°)/h或3 (°)/h。该仿真用例说明了本文方法可以在不同计算周期下，平衡方程可能无法诊断故障，但本文方法均可正确选出最优陀螺组。

图4给出了计算周期0.2 s时的两种故障情况的残差时间曲线，图5给出了陀螺的选取情况。对比图2(a)，可以看出：零偏变化越大，残差变化越迅速，也能越快检测出故障陀螺。尽管选取较小的计算周期，在陀螺零偏发生变化时，估值仍能够反映零偏的真实变化，当零偏变化量较大时，诊断会更快。

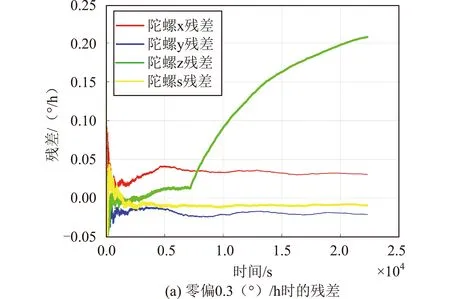
图4 零偏变化不同时残差曲线

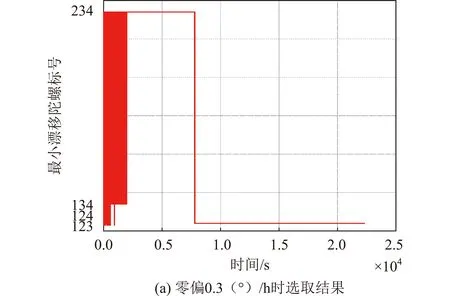
图5 陀螺选择情况时间曲线

图6给出了零偏变化到3 (°)/h时(突发卡死或停转故障时，陀螺输出变化更为剧烈，仿真情况与此相似)不同计算周期的陀螺平衡方程诊断情况时间曲线，可以看出，陀螺平衡方程只有在计算周期较大或零偏较大变化时才可能起作用。当计算周期较小时或零偏变化小时，平衡方程法无法对陀螺零偏的变化情况给出诊断。

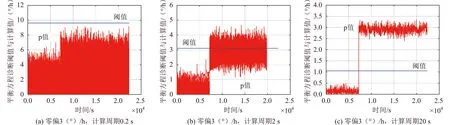
图6 平衡方程计算情况曲线

综上仿真情况，可以看出：①本文提出的基于估值的残差法可以实现无阈值的陀螺选取；②基于估值的残差法在陀螺选取的准确性及快速性上不逊于平衡方程，且能检测较小的零偏变化；③由于平衡方程法逻辑算法简单且具有较好的应用经验，选用平衡方程法与估值法构成二层检测法，既能保证算法的可靠性也能选用最佳性能陀螺组；④计算周期的选取与可检测的性能密切相关，应根据陀螺特性及系统设计期望综合选取。

4 结束语

本文提出的无阈值陀螺选用方法不仅可以用于较大故障的陀螺剔除，也可以在陀螺零偏变化较小时选出性能最佳的陀螺组合。不仅适用于5个及以上的陀螺选取问题，也适用于4个陀螺的欠冗余选取问题。由于方法中既继承了平衡方程法的可靠经验，也能显著提升陀螺组合的性能，对提高卫星在轨定姿精度具有积极作用。同时，该方法适用于陀螺数量小于5个的情况；对于减少陀螺配置数量、提升卫星系统自主诊断能力具有重要意义。