基于温度实验的永磁同步电机损耗分离方法
骆凯传 师 蔚 张舟云
基于温度实验的永磁同步电机损耗分离方法
骆凯传1师 蔚1张舟云2
(1. 上海工程技术大学城市轨道交通学院 上海 201620 2. 上海电驱动股份有限公司 上海 201806)
为了研究内置式永磁同步电机在不同工况及不同温度情况下永磁电机各部分的损耗,首先,基于运行参数及温度对永磁电机各损耗进行仿真,并建立基于运行参数及温度的损耗模型。在永磁电机定转子各部分预埋测温元件,采用变工况温度实验进行永磁电机温度及损耗实验。然后,结合电机导热特性及测温元件布置建立永磁电机等效热网络模型,通过永磁电机在不同工况下的温度及总损耗实验结果,采用扩展卡尔曼滤波算法对永磁电机进行各损耗的分离。最后,将分离出来的损耗与实测总损耗和计算损耗模型结果分析进行对比,验证损耗分离方法及基于工况和温度损耗模型的正确性。
永磁同步电机 热网络 扩展卡尔曼滤波 温度实验 损耗分离
0 引言
高密度永磁电机具有高效率、高密度、调速范围广等优点,因此被广泛应用于牵引领域。但由于损耗及散热条件相对较差,温升是主要的难题之一。过高的温升会造成定子绕组绝缘层失效、永磁体永久性退磁以及损耗变大等一系列问题,将直接影响永磁电机的电磁性能,甚至影响永磁电机的使用寿命[1-3]。因此,研究永磁电机的损耗对研究电机温升问题,进行优化设计改善温升,根据各部分损耗对电机进行各部分温度监测[4-5],特别对于永磁电机转子温度在线监测具有重要意义。
根据损耗产生的来源,永磁电机内部的损耗主要有铁心损耗、永磁体涡流损耗、绕组铜耗、机械损耗等几类。对于永磁电机损耗的计算和分离,国内外很多学者做了大量的研究。目前,常用的铁耗计算模型是由Bertotti提出的经典三项铁耗模型,现在铁耗模型也都是基于经典三项模型的改进模型。文献[6-8]采用考虑旋转磁场、高次谐波、趋肤效应、磁路饱和、小磁滞环路下的永磁电机铁心损耗模型。文献[9-10]则推导了考虑脉冲宽度调制(Pulse Width Modulation, PWM)逆变器供电高次谐波电流影响的气隙磁通密度和谐波损耗的解析计算模型。文献[11]则研究了定子铁心各部分的损耗分布及随负载变化的规律。
永磁体涡流损耗主要由齿槽、气隙等产生的空间谐波及电枢电流中的时间谐波造成,计算方法主要有解析计算法和有限元分析法两种。文献[12-13]考虑齿槽效应、槽口位置,推导了基于空间谐波引起的永磁体涡流损耗解析计算模型。文献[14]通过建立一个四维谐波扩散方程,用图像法和四维傅里叶变换相结合解析计算永磁体涡流损耗。由于磁场空间分布的不均匀以及饱和效应,解析法很难对永磁体涡流损耗进行精确的解算。文献[15-16]利用三维有限元分析法,考虑了斜极、永磁体分段等因素,仿真分析了电流的时空谐波分量造成的永磁体涡流损耗。但三维有限元计算量大、效率不高。文献[17]则提出结合有限元分析法和解析计算法,用于高效计算永磁体涡流损耗。文献[18]针对电机内部低频永磁体涡流损耗及永磁体中谐波损耗分别采用高效有限元分析和频域小信号分析结合永磁体涡流损耗模型进行高效计算。
基于以上永磁电机铁心损耗及涡流损耗的分析结论都揭示了无论铁心损耗还是永磁体涡流损耗都与电机内部电磁场时空分布直接相关。永磁电机工况变化、永磁体温度的变化导致永磁体工作点的变化是引起永磁电机磁场分布变化的直接因素,但鲜有文献直接建立考虑永磁体温度、运行工况的损耗模型。这一模型对永磁电机全域空间的优化以及温度的在线估计具有重要价值。
在永磁电机通过实验进行损耗分离验证方法研究中,多是通过电机空载和负载的实验对比,依据能量守恒定律进行损耗逐个分离。文献[19]根据功率和电流关于电压的双“V”曲线,对空载损耗和负载损耗分离实验进行优化来分离出各个损耗。然而该方法分离出绕组铜耗、机械损耗、铁耗和杂散损耗,没有分离出转子的损耗,且仅在额定负载工况下进行损耗分离。转子损耗包括永磁体涡流损耗和转子铁心损耗,其值相对较小且不易测量,但转子散热困难,易造成永磁体温度过高,从而增加了永磁体不可逆的退磁风险[12-18],严重影响电机的性能和寿命,因此,转子损耗分离是永磁电机损耗分离的难点。文献[20]在空载条件下把总损耗减去空气摩擦损耗、铁心损耗和铜耗得到转子涡流损耗。文献[21]通过原动机拖动永磁电机在不同转速下运行,根据反电动势、永磁体温升及其涡流损耗的关系得到永磁体涡流损耗大小,因此分离出的结果只符合空载条件。文献[22]则研制了一套闭环磁场测量系统,对永磁材料的损耗进行了变频测量,但这一闭环测量系统无法准确模拟永磁电机内部的磁场分布。文献[23]通过无线测温测得永磁体的温升,通过永磁体实验前后温差分离出永磁体的涡流损耗,再通过定制无磁性转子电机实验进行对比,分离出机械损耗、定转子损耗;但仅验证了一种工况下的损耗,且永磁体涡流损耗分离依据于实验过程的温升,未考虑永磁转子本身热量传递。
本文首先对永磁电机损耗提出建立基于运行参数及温度的损耗分析方向,针对基于运行参数及永磁体温度对铁心损耗、永磁体涡流损耗进行有限元仿真分析;针对线圈铜耗及机械损耗进行解析分析。并通过回归分析方法建立了永磁电机基于运行参数及温度的损耗模型。接着搭建永磁电机温升及损耗分析实验平台,根据电机热特性以及实验台温度测点分布,建立永磁电机的等效热网络浅灰箱模型。通过电机温升实验平台采集的节点温度结合热网络模型,采用扩展卡尔曼滤波算法对各种损耗进行分离,同时提高损耗分离系统的鲁棒性及准确性。此损耗分离方法不仅可以分离出较难分离的转子损耗且适用于变工况的损耗分离。最后用分离结果与电机总损耗测试结果和计算结果进行分析和对比,验证损耗分离方法的可行性和基于运行参数及温度损耗计算模型的准确性。
1 基于运行参数及温度的永磁电机损耗模型
本文以一台额定功率45kW、峰值功率90kW的内置式高密度永磁同步电机为研究对象,该电机为内置“V”型转子磁极结构,其1/8永磁电机模型如图1所示,永磁电机的基本参数见表1。
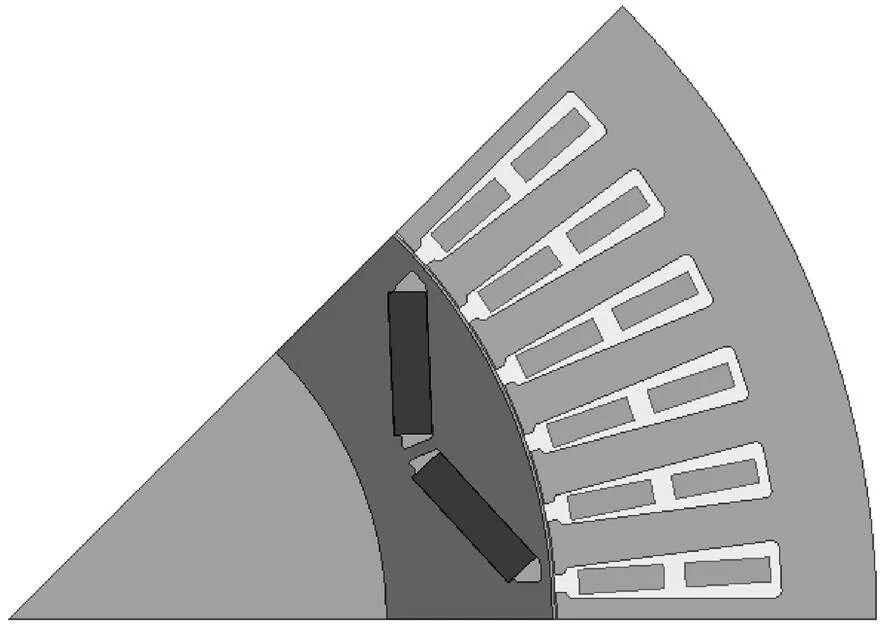
图1 永磁同步电机模型
表1 永磁电机的基本参数
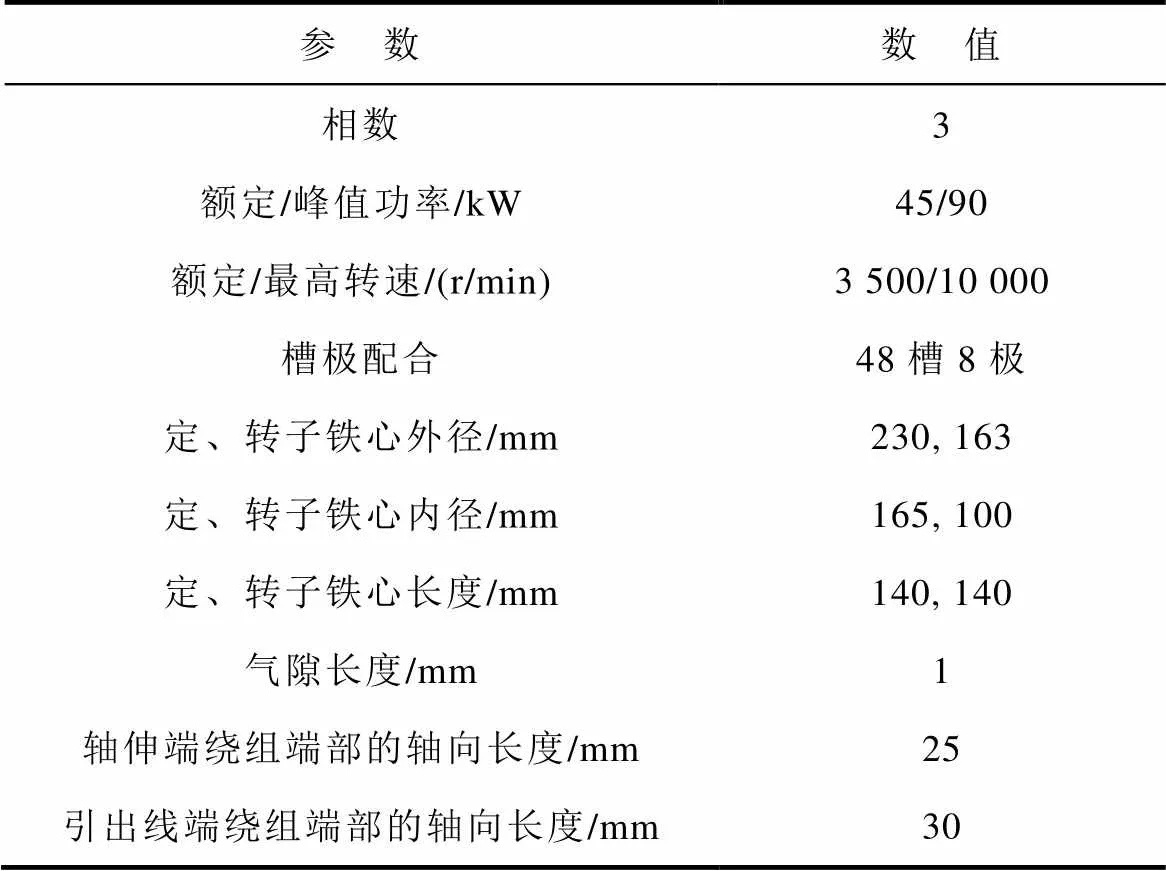
Tab.1 Basic parameters of the permanent magnet motor
为了考虑逆变器PWM波带来的高次电流谐波对电机各部分损耗产生的影响[9],通过对电机不同工况下的实验,测试逆变器供电下电机电流代替正弦电流,作为各损耗计算模型的输入电流。图2为逆变器在开关频率为10kHz,电机峰值功率运行时的电流波形。
1.1 铁心损耗
铁心损耗受高次谐波、磁路饱和、旋转磁化等因素的影响,目前常用的铁耗计算模型是由Bertotti提出的包含磁滞损耗、经典涡流损耗及异常损耗三项组成的铁心损耗模型,有
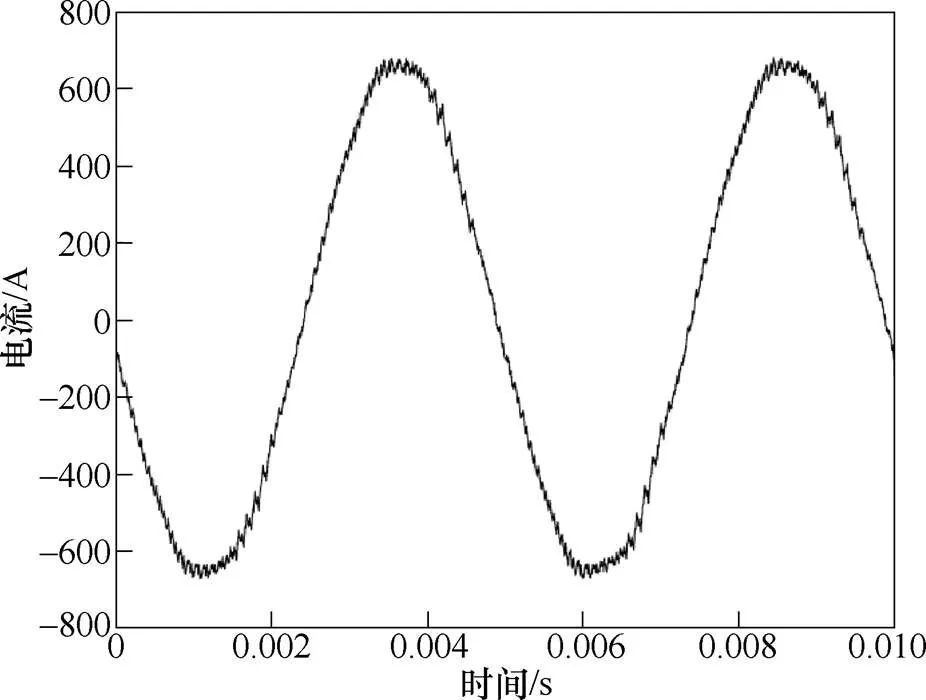
图2 变频器供电电流波形

式中,Fe为铁心损耗;h、c、a分别为磁滞损耗、涡流损耗和异常损耗;h、为磁滞损耗系数,通常为1.6~2.2;c、a分别为涡流损耗系数、异常损耗系数;m为磁通密度幅值;为磁场交变频率。
当以实测电流输入有限元电磁分析软件对铁心损耗计算并分析发现,硅钢片温度对铁心损耗产生影响很小,可忽略不计。图3为电机转速=3 500r/min,定子直轴电流d=-150A,定子交轴电流q=290A的定工况下,不同永磁体温度的定转子铁心损耗计算值。由图3可发现,定转子铁心损耗都会随着永磁体温度的上升而减小,其中定子铁心在20℃时计算值为627.6W,在180℃时为598.6W;转子铁心在20℃时计算值为55.4W,在180℃时为54.1W。分析发现,这主要是由于永磁体温度上升而造成工作点下降,铁心中的磁通密度有所减小,使损耗下降。其中,永磁体温度对转子铁心损耗的影响较小,可忽略不计。
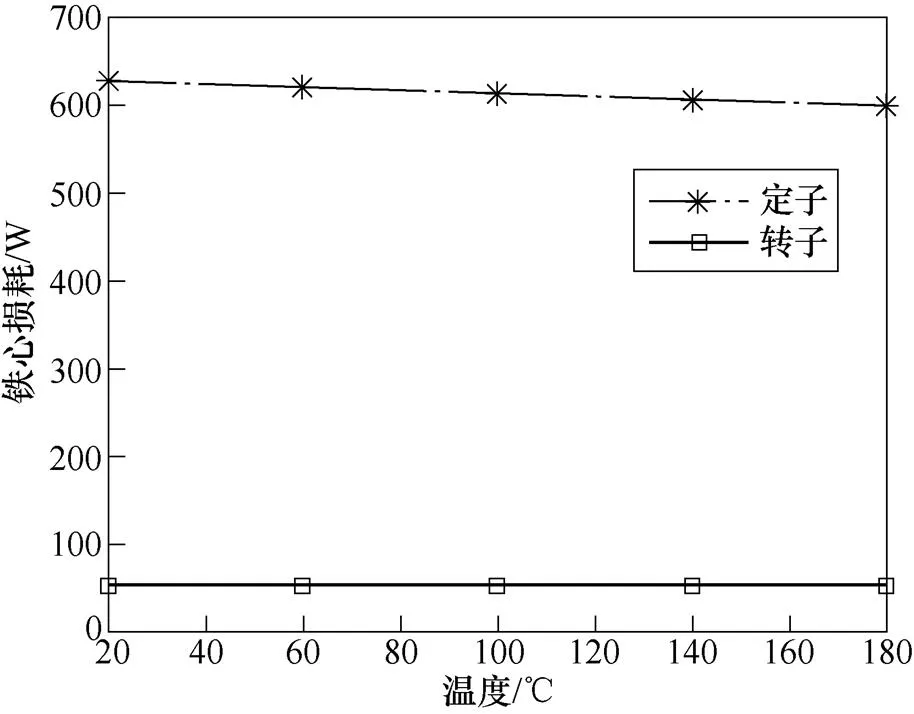
图3 定工况下不同永磁体温度的铁心损耗计算值
当输入永磁电机电流频率上升时,永磁电机转速不断上升,在相同负载情况下,铁心损耗不断上升。图4为永磁体温度在100℃时,d=-150A,q= 290A的定电流工况下铁心损耗随转速变化曲线。
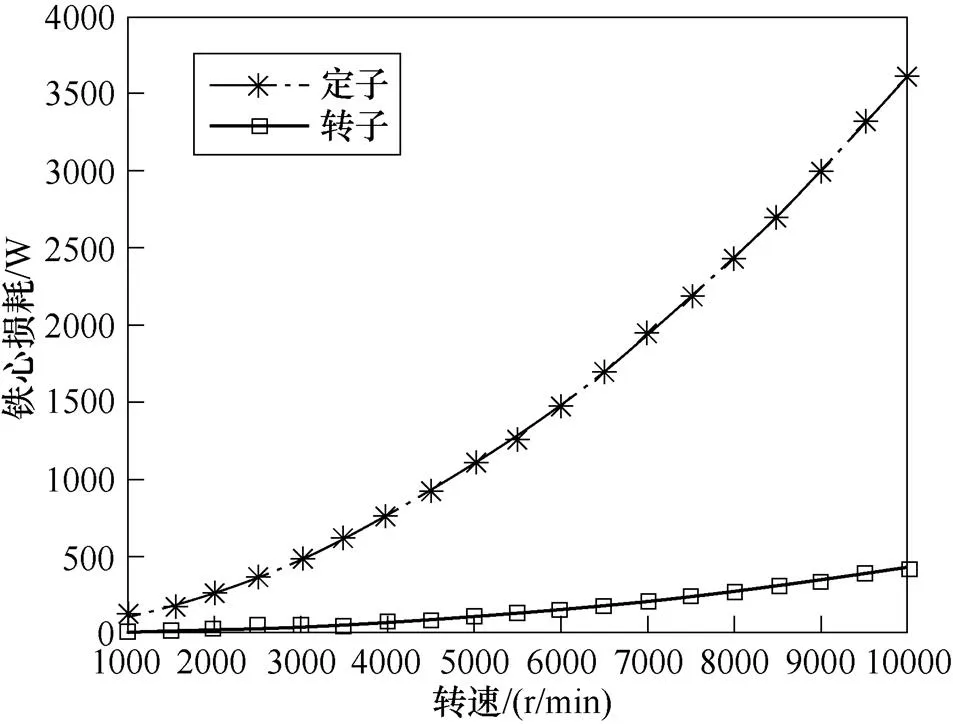
图4 定电流和温度下铁心损耗随转速变化计算值
同时,也可以得到定转速、定温度下不同输入电流下的定子、转子铁心损耗。图5为永磁体温度在100℃时,转速在3 500r/min定转子铁心损耗随d、q的变化曲面。
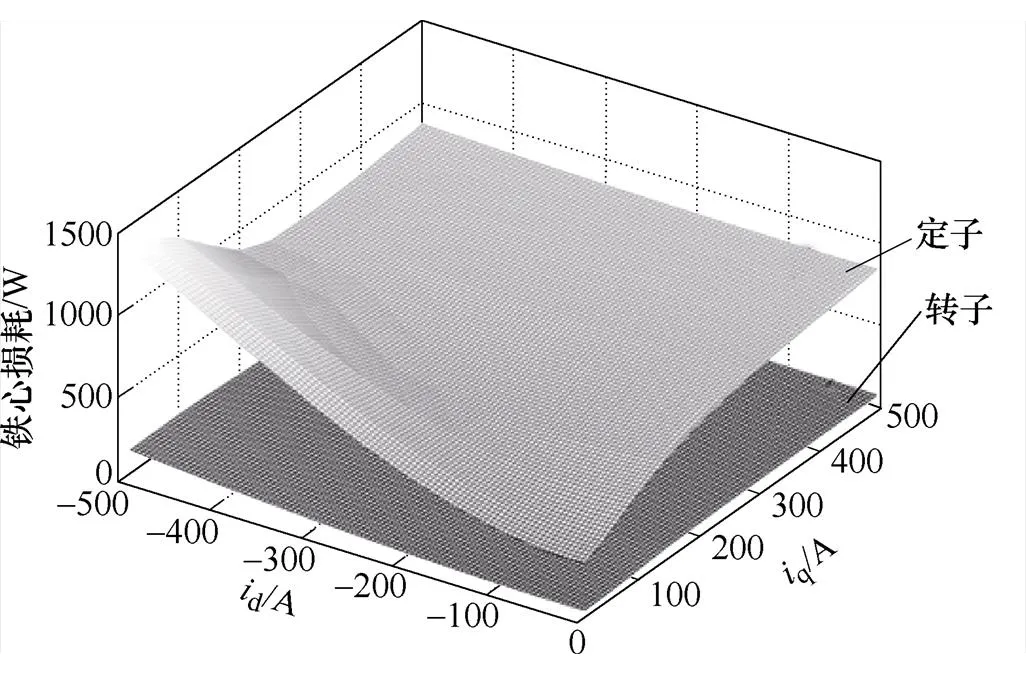
图5 不同输入电流下的铁心损耗分布
通过对不同永磁体温度、不同转速、不同输入电流的定子、转子铁心损耗及转子铁心损耗进行仿真,并对仿真结果进行二项式回归,即可得到基于运行参数d、q、及永磁体温度的定、转子铁耗计算模型分别为
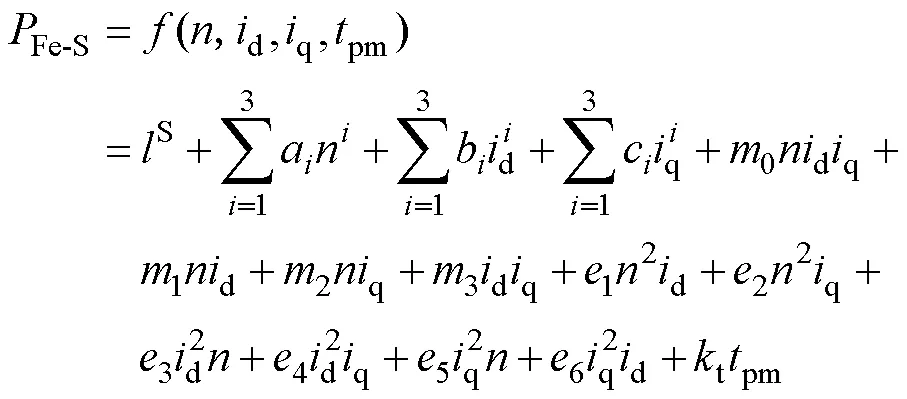
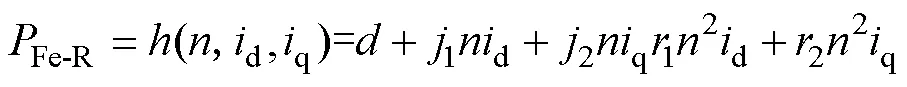
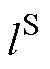
表2 铁心损耗回归参数

Tab.2 Regression parameter table of core loss
1.2 永磁体涡流损耗
永磁电机因电机齿槽的存在,定子磁动势的非正弦分布及定子绕组相电流有高次谐波等各种因素的影响,会在气隙磁场中产生空间和时间谐波分量,这些谐波成分会在转子永磁体产生涡流损耗[14-15]。永磁体涡流损耗具体计算模型为
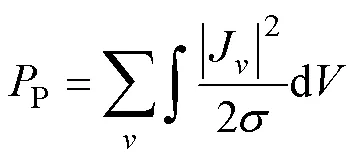
式中,P永磁体涡流损耗;J为第次谐波涡流幅值;为永磁体电导率;为永磁体体积。
对于永磁体的涡流损耗,通过不同工况下的实测电流输入有限元仿真模型后可得,转子永磁体在不同温度时,由于永磁体工作点的变化,导致永磁体内动态磁通密度变化,根据法拉第电磁感应定律可知,变化的磁通可以产生感应电流,使得感应电流趋于永磁体表面经过,进而使永磁体表面的电流增加及表面电流密度增加,从而对永磁体涡流损耗产生影响,图6为=5 500r/min,d=-150A,q=290A的定工况下,不同永磁体温度与永磁体涡流损耗计算关系曲线。
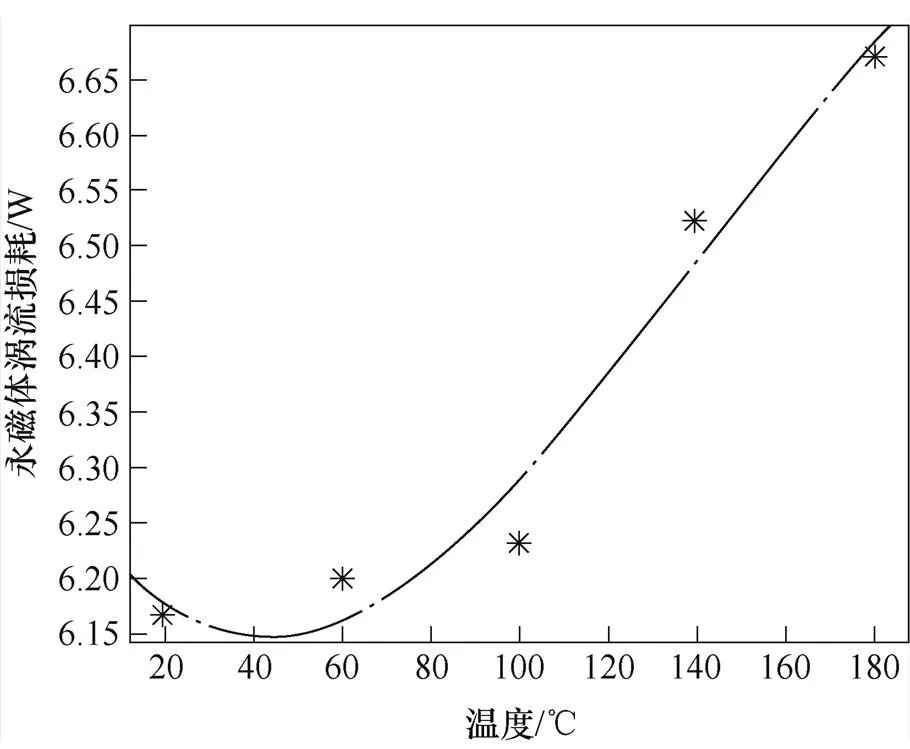
图6 定工况下不同永磁体温度与永磁体涡流损耗计算关系曲线
由于输入电机电流频率的上升导致永磁体涡流损耗随电机转速增大而增大,图7为永磁体温度在100℃时,d=-150A,q=290A的定电流工况下永磁体涡流损耗随转速变化曲线。
同时,可以得到定转速、定温度下不同输入电流下的永磁体涡流损耗。图8为永磁体温度在100℃转速在3 500r/min时,永磁体涡流损耗随定子直轴电流d、交轴电流q的变化曲面。
通过对不同温度、不同转速、不同输入电流的永磁体涡流损耗进行仿真,并对仿真结果进行回归,即可得到基于运行参数及永磁体温度的永磁体涡流损耗模型为
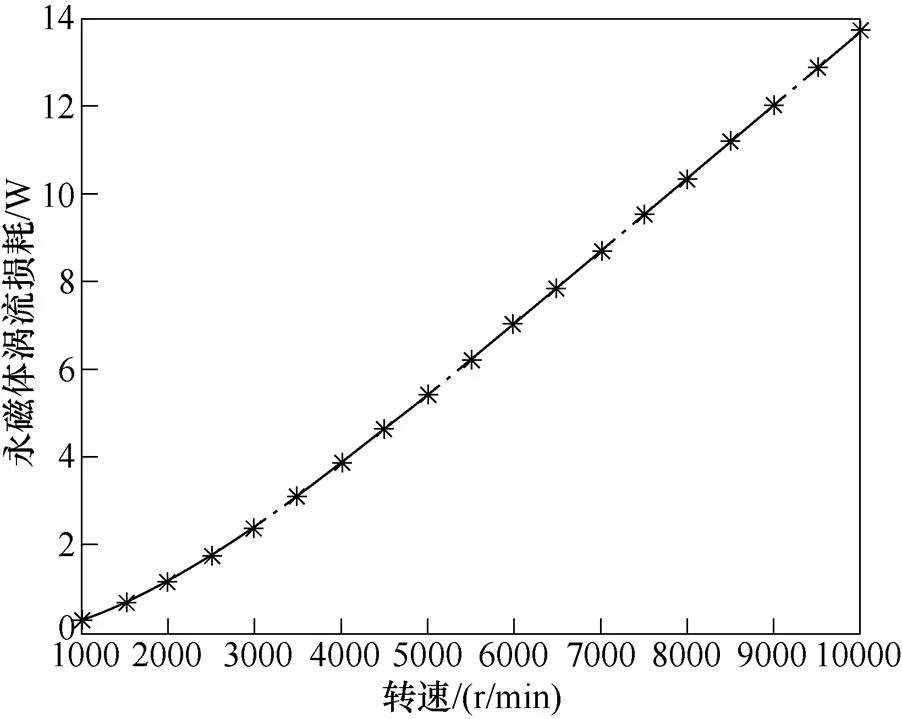
图7 定电流和温度下永磁体涡流损耗与转速关系
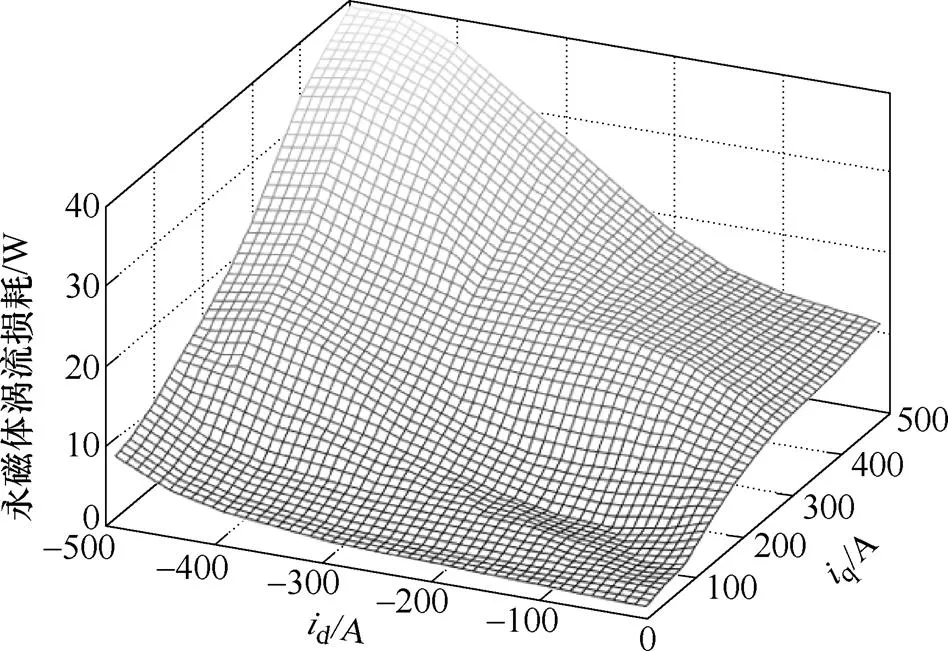
图8 定温度下永磁体涡流损耗与id-iq关系
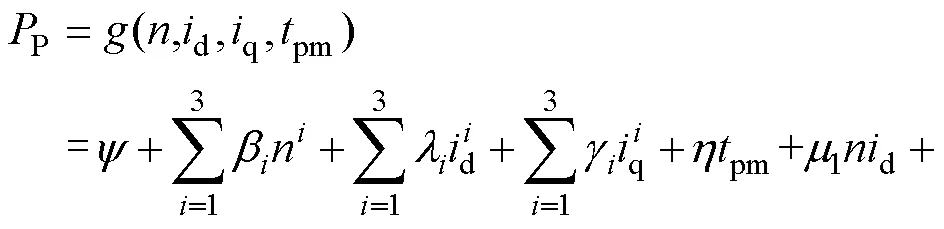

1.3 定子铜耗
绕组的铜耗是由于电流通过绕组产生的电阻损耗,相电阻对温度的依赖性极强,同时考虑绕组槽内和端部温升分布不同,将绕组铜耗分为槽内和端部两部分。建立基于运行参数及温度的槽内绕组和端部绕组的铜耗分别为
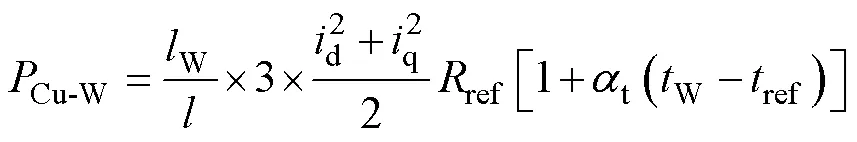

表3 永磁体涡流损耗回归参数
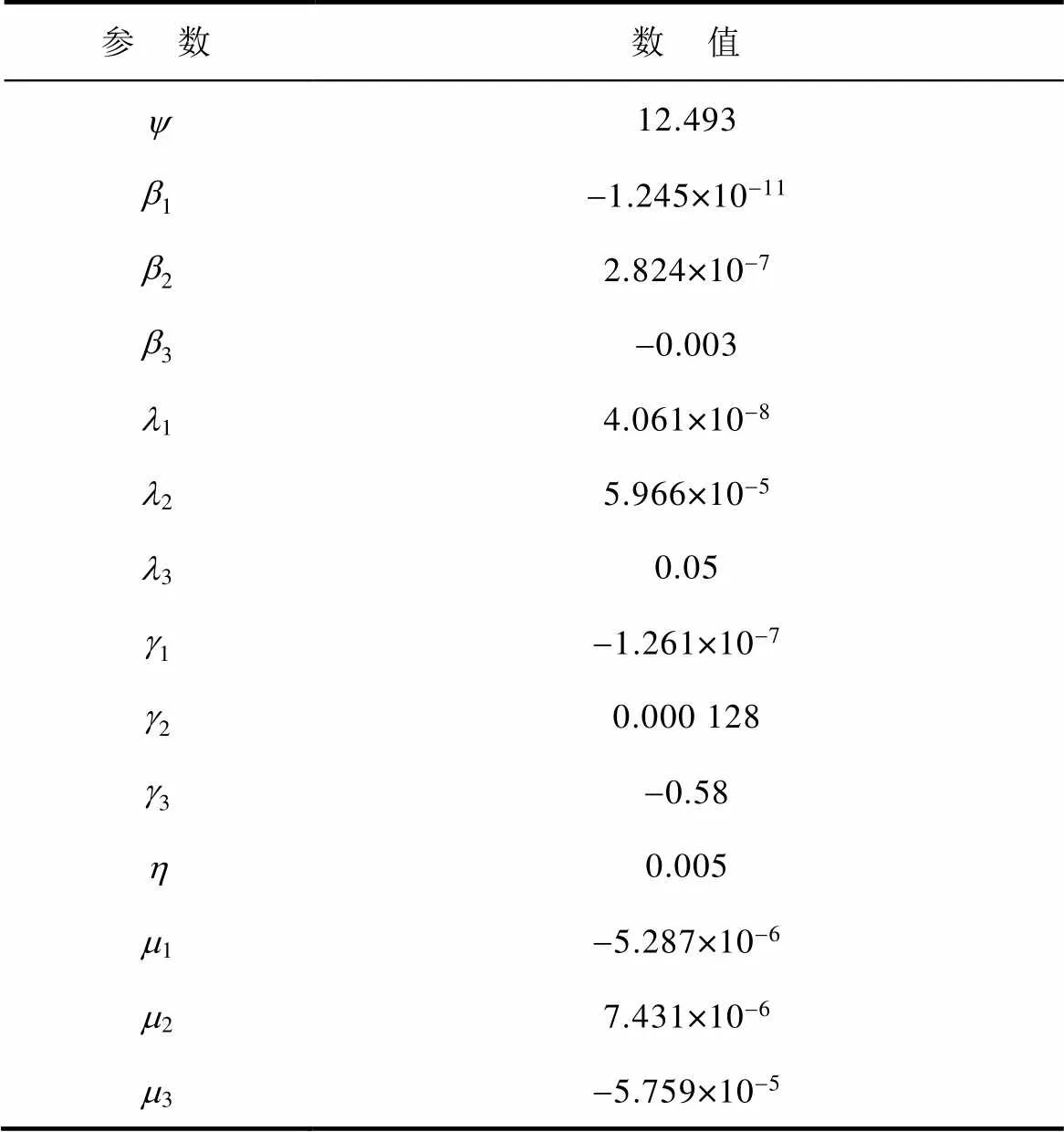
Tab.3 Regression parameter table of permanent magnet eddy current loss
式中,Cu-W为槽内绕组铜耗;Cu-EW为端部绕组铜耗;为绕组总长度;W为槽内绕组长度;EW为端部绕组长度;ref为参考绕组阻值;t为绕组的温度系数;W为槽内绕组温度;EW为端部绕组温度;ref为参考温度。
在电机运行过程中,磁场是变化的,绕组存在趋肤效应和邻近效应,其对铜耗也存在影响,但因电机线径而忽略绕组的趋肤效应和邻近效应。
1.4 机械损耗
电机机械损耗由轴承摩擦及风阻的轴承损耗和风磨损耗构成。轴承摩擦损耗为
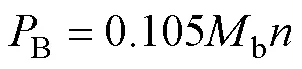
式中,B为轴承损耗;b为轴承的总摩擦力矩。轴承的总摩擦力矩分为四个部分,有

式中,rr为滚动摩擦力矩;sl为滑动摩擦力矩;seal为密封件的摩擦力矩;drag为润滑油润滑脂拖拽、涡流和飞溅等导致的摩擦力矩。
通过各种摩擦力矩的计算模型,可知轴承损耗主要与电机的扭矩、转速以及温度有关;而温度对轴承损耗的影响主要体现在滚动摩擦力矩上,当温度达到90℃影响到润滑脂低粘度时,损耗会急剧变大,电机轴承损耗可以忽略温度的影响。如图9所示为轴承全工作域下的损耗关系。
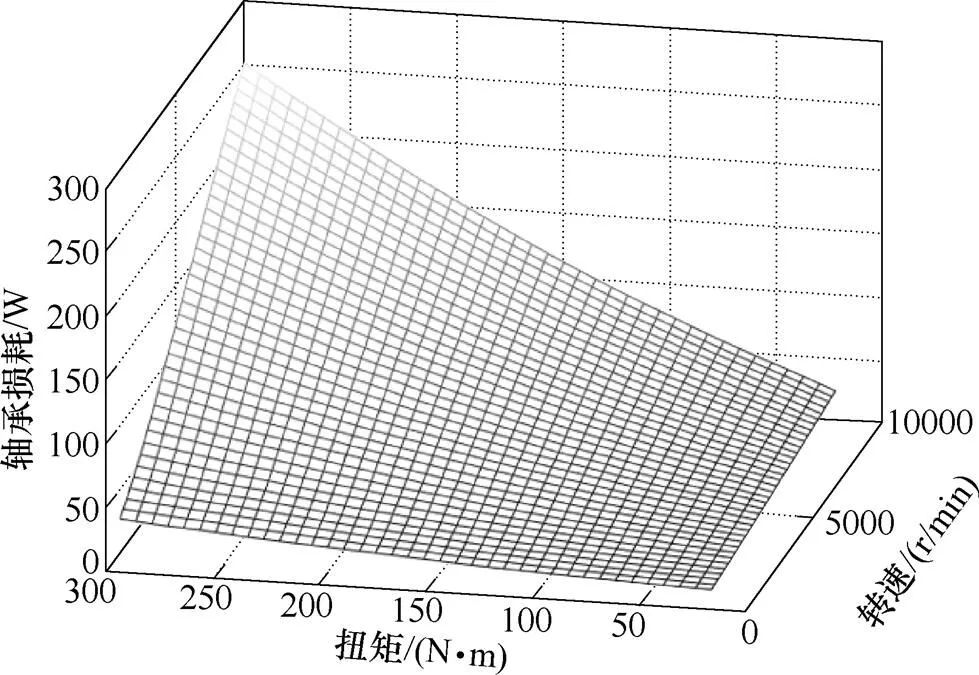
图9 轴承损耗与扭矩-转速关系
风磨损耗计算式为
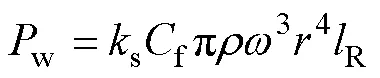
式中,w为风磨损耗;s为转子表面粗糙度,表面光滑时为1;f为流体的摩擦因数;为气体密度;为转子工作时的角速度;为转子半径;R为转子的轴向长度。风磨损耗主要受转速的影响,随着转速的增大而增大。
2 基于温度实验的热网络模型
2.1 温度实验台构建
根据研究的永磁电机,设计一个用于温度测量及损耗分离实验平台,其中温度测点主要包括永磁电机的定子绕组、机壳、进出水道、环境以及转子永磁体,全部采用接触式传感器直接测量,测试点布置示意图如图10所示。对于转子部分测温,通过在永磁体与转子铁心之间开槽安置温度传感器,转子开槽示意图如图11所示。
实验平台主要包括被测电机、发电机、逆变器、控制器、功率分析仪、温度处理及采集模块、直流电源和自动水冷控制箱。转子温度通过转子同步旋转的温度处理模块及发射模块将实时的温度数据传输至测温软件,模型电机实验平台如图12所示。
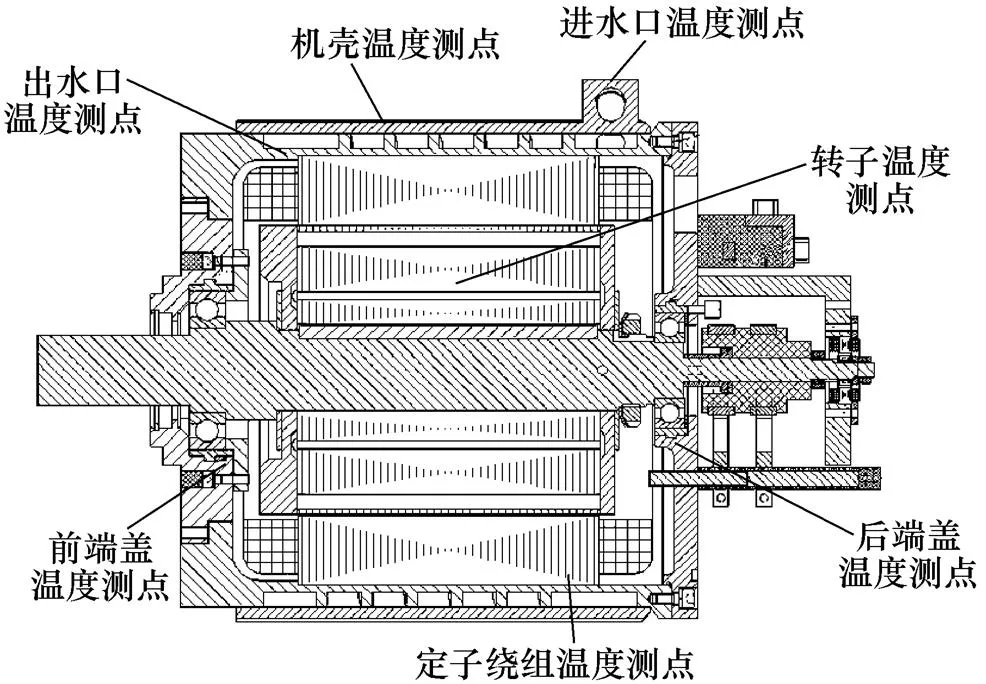
图10 电机温度测试点分布示意图
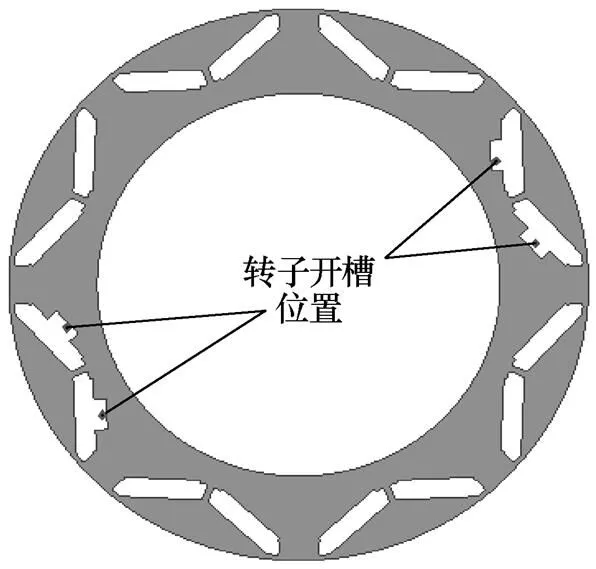
图11 转子开槽示意图

图12 模型电机实验平台
2.2 损耗识别热网络模型
根据研究电机的结构尺寸、热流方向、热源及测温元件分布和损耗分离的需要,建立5节点集总参数热网络(Lumped Parameter Thermal Networks, LPTN)模型。永磁体嵌入在转子铁心内部,且转子铁心损耗主要为铁心涡流损耗,因此将转子铁心和永磁体简化为转子区域。即将电机分为定子铁心、定子绕组槽内部分、定子绕组端部部分、转子、轴承5个区域模块,所建5节点等效热网络模型示意图如图13所示。
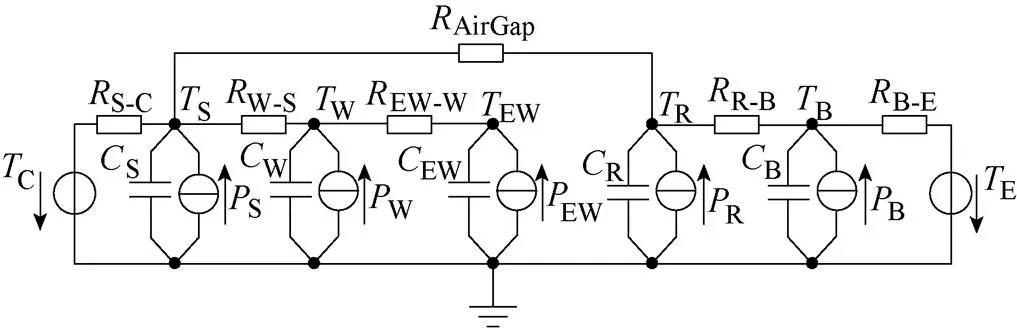
图13 等效热网络模型示意图
网络中5个节点分别代表模型电机5个区域的温度。定子铁心温度节点S通过热阻W-S和槽内绕组温度节点W相连,通过气隙热阻AirGap与转子温度节点R相连,通过热阻S-C与电机冷却水道入水口温度C连接。轴承温度节点B通过热阻R-B与转子温度节点R相连,通过热阻B-E与环境温度E连接。定子端部绕组温度节点EW通过热阻EW-W与定子槽内绕组温度节点W相连。S、W、EW、R、B分别为简化定子铁心热容、定子槽内绕组热容、定子端部绕组热容转子热容和转子轴承热容。永磁电机内部的热源主要为各种损耗,其中,S、W、EW、R、B分别为定子铁心损耗、定子槽内绕组损耗、定子端部绕组损耗、转子涡流损耗以及轴承损耗,其中转子涡流损耗包括转子铁心损耗和永磁体涡流损耗。
将图13所示LTPN模型建立热平衡方程,可建立状态空间方程,表示为
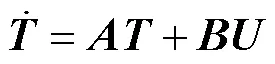
其中
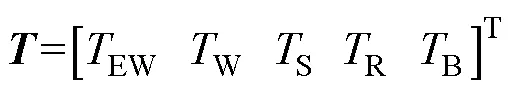
式中,为状态空间方程输入,包含各种损耗、环境及水道温度;为5节点温度状态变量;和分别为热阻和热容共同组成的状态转移矩阵和输入矩阵。
2.3 热容及热阻模型
2.3.1 热容
以上热网络模型中热容根据传热学理论进行计算,计算公式为

式中,为物体密度;P为物体体积;c为物体的比热容。通过计算得到热网络模型中的热容数值见表4。
表4 热网络定值热容

Tab.4 Thermal network fixed heat capacity[单位: J/(kg·K)]
2.3.2 热阻
忽略热辐射,根据热传递方式可将等效热网络中的热阻分为热传导电阻和热对流电阻,W-S、EW-W、S-C为热传导电阻;AirGap、R-B、B-E为热对流电阻。节点之间的热传导热阻为
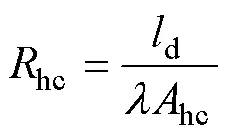
式中,hc为热传导热阻;d为两个节点之间的距离;为材料的导热系数;hc为传导区域的面积。
两个节点之间的热对流热阻为
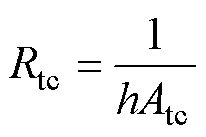
式中,tc为热对流热阻;为对流换热系数;tc为热对流区域的面积。
3 基于温度实验的损耗分离方法
根据5节点的LTPN模型、永磁电机热阻和热容参数,进行永磁电机不同工况电机实验,通过实验得到测试点温度即可分离不同工况下损耗值。为了提高损耗分离的鲁棒性及损耗分离精度,本文使用了扩展卡尔曼滤波算法来分离热网络模型中的各损耗。
3.1 扩展卡尔曼滤波算法的损耗分离模型
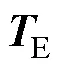
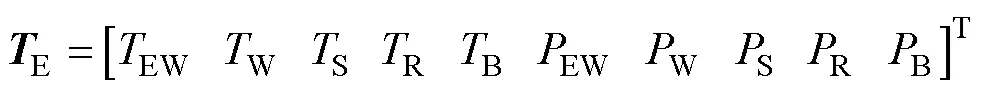
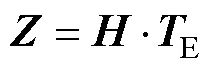
其中
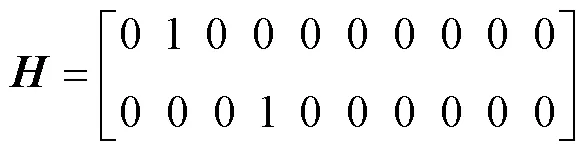
式中,为观测矩阵。
将状态空间方程离散化可表示为
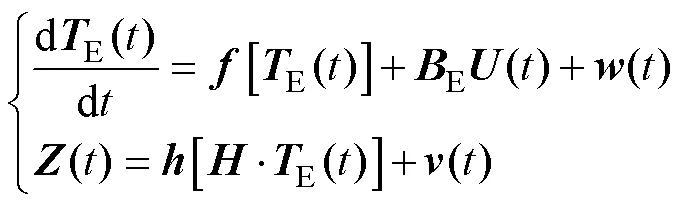
其中
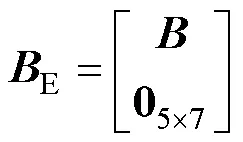
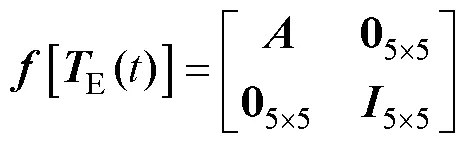
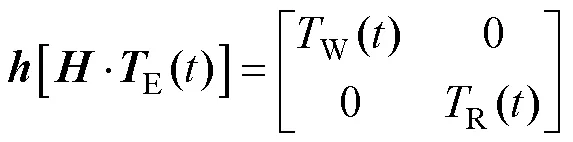
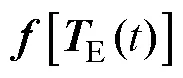
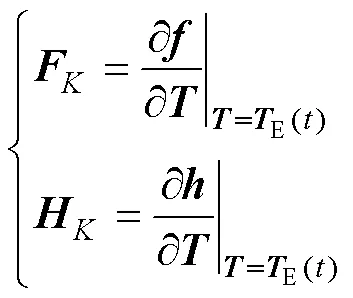
状态转移矩阵/K-1为
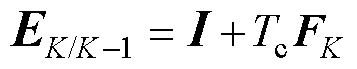
式中,为单位矩阵;c为采样周期,c=1s。
线性化后的数学模型为
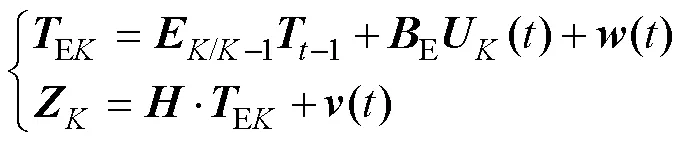
式中,EK为t时刻的增广状态矩阵;()为t时刻的输入矩阵;为t时刻的观测矩阵。
离散型扩展卡尔曼滤波方程包括每个运算周期状态预测和状态更新两个部分,状态预测如式(24)所示,状态更新如式(25)所示。
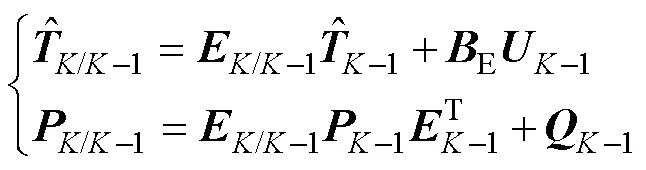
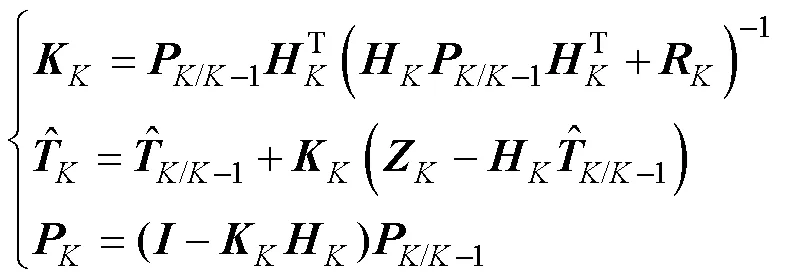
3.2 永磁电机损耗分离流程
通过永磁电机不同工况温度实验,使用扩展卡尔曼滤波方法即可进行永磁电机损耗分离,流程如图14所示。根据2.2节的LTPN网络模型,将电机实时冷却介质的温度C、外部环境温度E、电机定子绕组温度W以及电机转子温度R、交直轴电流d、q、电机转速输入网络模型,结合扩展卡尔曼滤波进行模型,从而分离出损耗值,具体分离流程如图14所示。
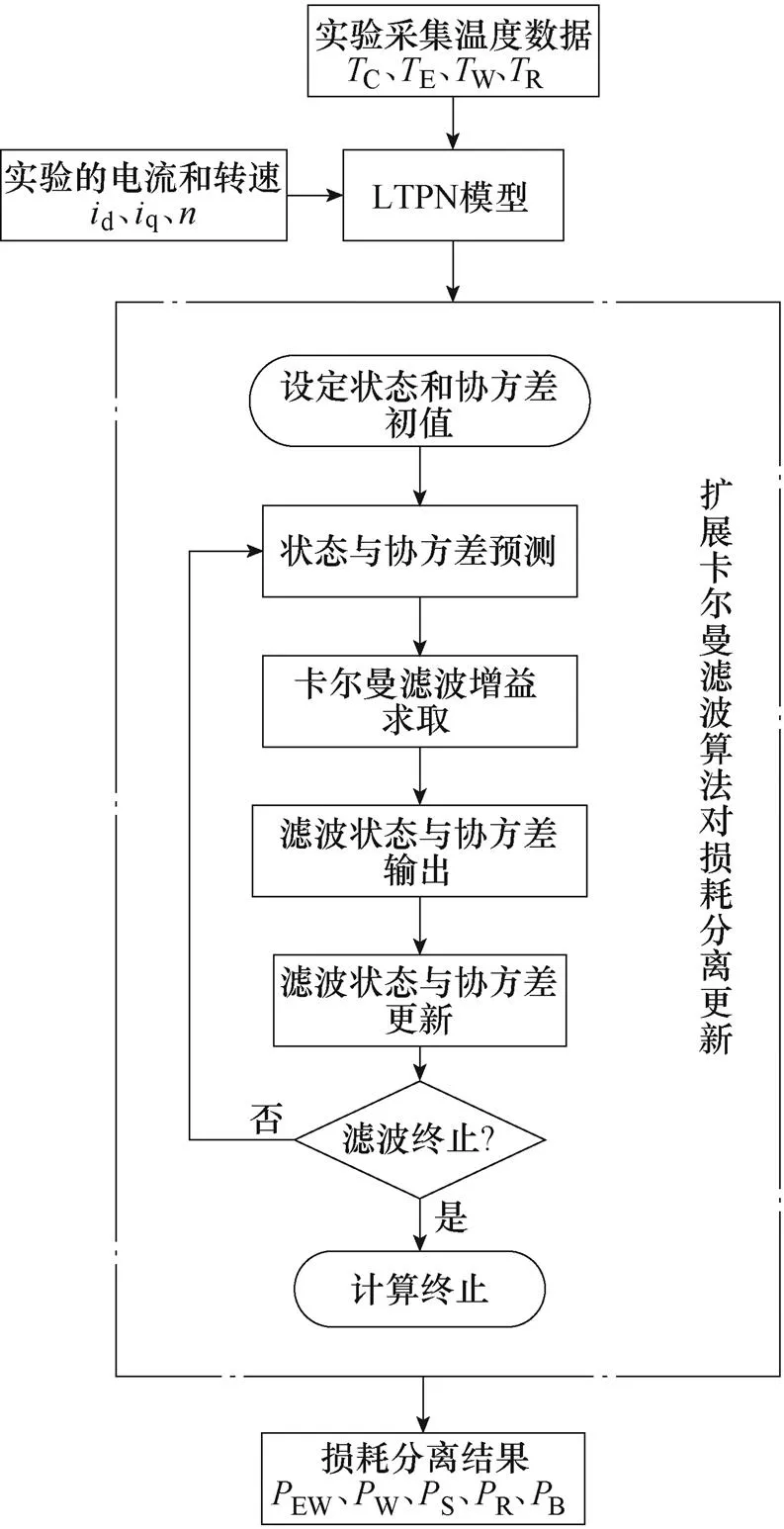
图14 损耗分离流程
4 基于温度实验的损耗分离
4.1 永磁电机损耗分离
通过永磁电机温度实验台可测量电机的输入、输出功率、交直轴电流d、q电机转速及电机各部分实时温度,即可获得在不同温度下电机的总损耗total。其中,电机的输入功率由功率分析仪获得,功率精度为0.1%,输出功率是通过速度和扭矩传感器间接获得的,其总精度为0.1%。
首先电机在其额定条件运行的情况下进行测试,然后在各种其他工作条件下重复测试,包括电机连续工作在功率为45kW,转速为3 500r/min、3 750r/min、4 000r/min、4 500r/min;功率为55kW,转速为1 000r/min、2 000r/min、3 000r/min、3 500r/min、4 000r/min、4 500r/min。将实验采集到的温度、热容以及各个工况的热阻输入热网络模型中,利用扩展卡尔曼滤波算法将各部分损耗进行分离,电机运行在45kW,4 000r/min,工况转子温度为86℃下的损耗分离结果如图15所示。将分离出的各个损耗相加,并实测总损耗进行对比,结果见表5。从表5中可知,分离总损耗与实测总损耗相对误差在5%左右。
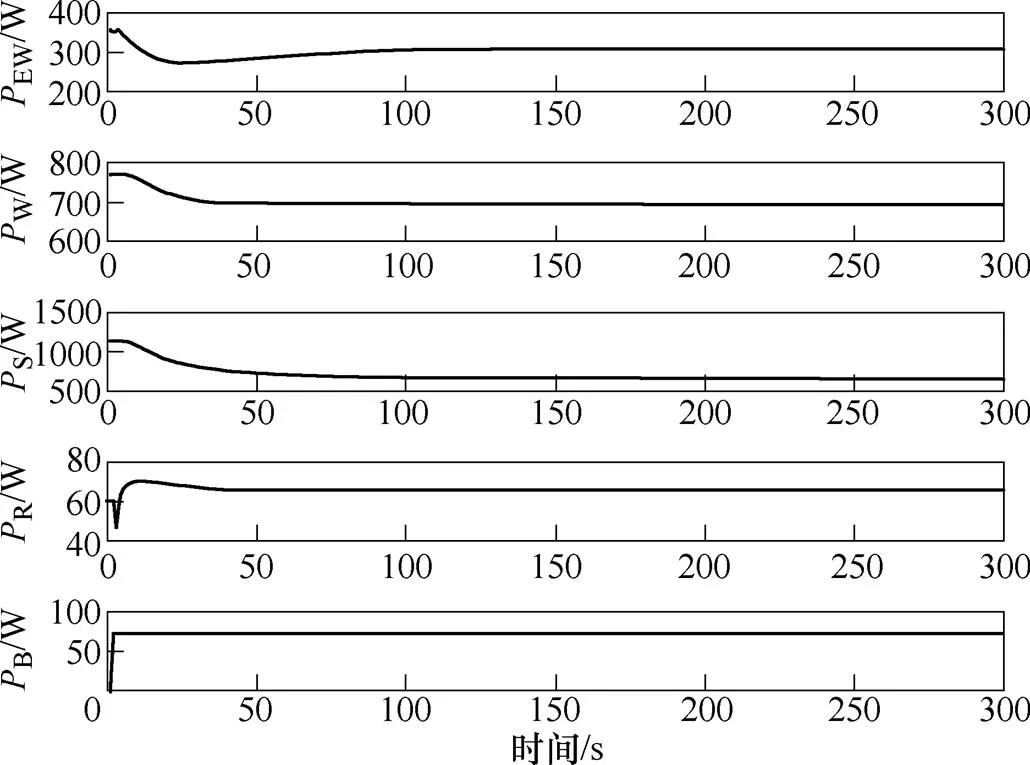
图15 TR=86℃, 45kW在4 000r/min工况下的损耗分离
表5 实测总损耗与分离结果总损耗结果
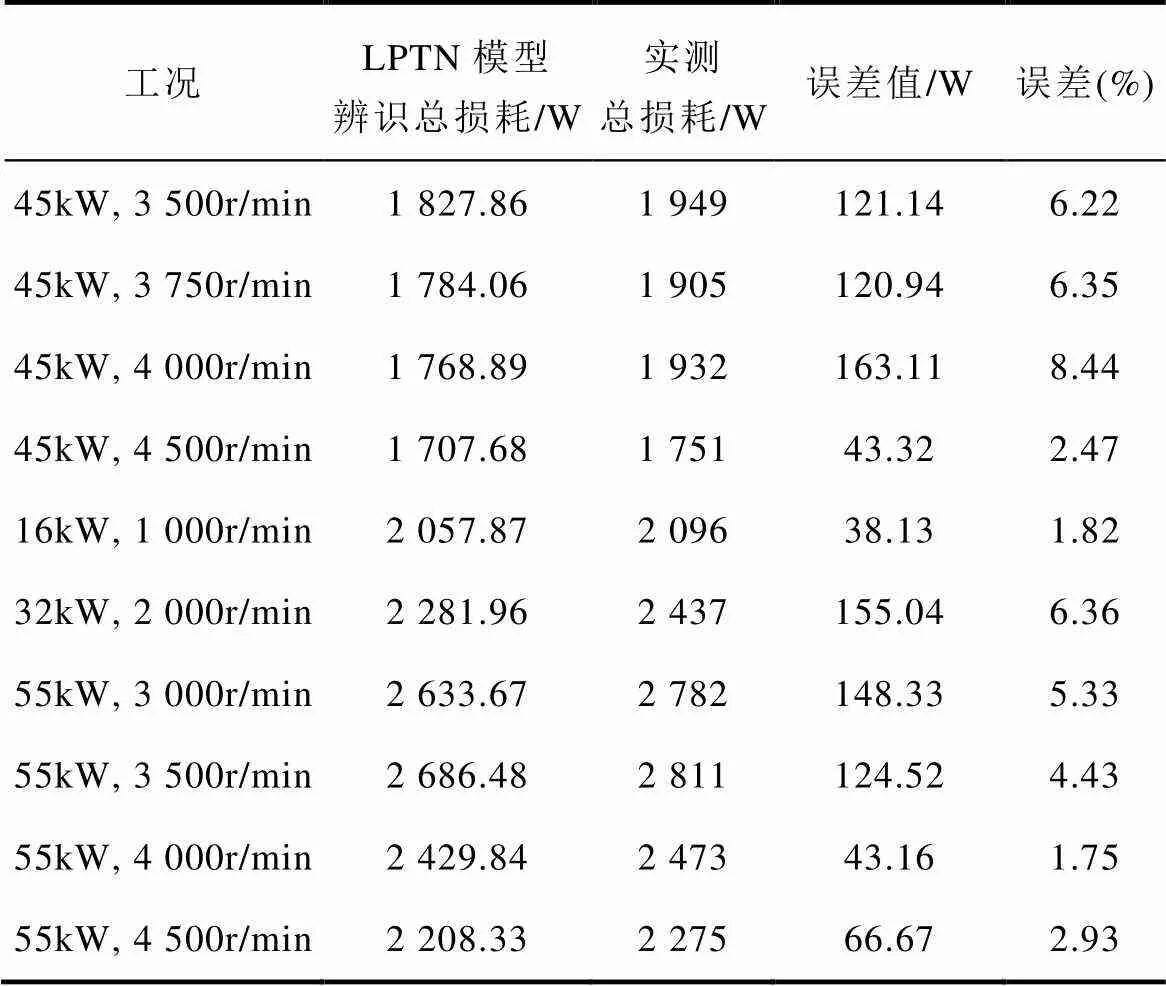
Tab.5 Measured total loss and separation result
通过对不同工况下,LTPN分离结果和基于运行参数及温度的损耗模型计算结果进行对比,分离法得到各个损耗值与计算值的相对误差在7%以内。对比损耗分离结果与计算结果,电机工作在45kW、55kW时不同转速下对比分别如图16、图17所示。电机工作在扭矩为154N·m的恒扭矩工况对比如图18所示。分析计算与实验分离损耗后,发现绕组铜耗方面端部绕组铜耗分离值比计算值略大,而槽内绕组铜耗分离值比计算值略小,总铜耗计算与实验保持一致,分析后认为计算模型属于集中模型,忽略槽内绕组与槽外绕组的热传导而造成一定误差。定子铁耗分离值比计算值大,分析主要是由于仿真计算忽略铁耗中异常损耗部分,但符合损耗计算模型中随着速度的增大定子铁心损耗增大,不同功率下及转矩下铁心损耗也符合随着交直轴电流的增大而增大。转子涡流损耗和轴承损耗的分离值也比计算值大4W左右,其误差值在合理范围之内,其中转子涡流损耗受转速影响较大,随着转速的上升持续上升,同时不同功率下及转矩下转子涡流损耗随着交直轴电流的增大而增大。
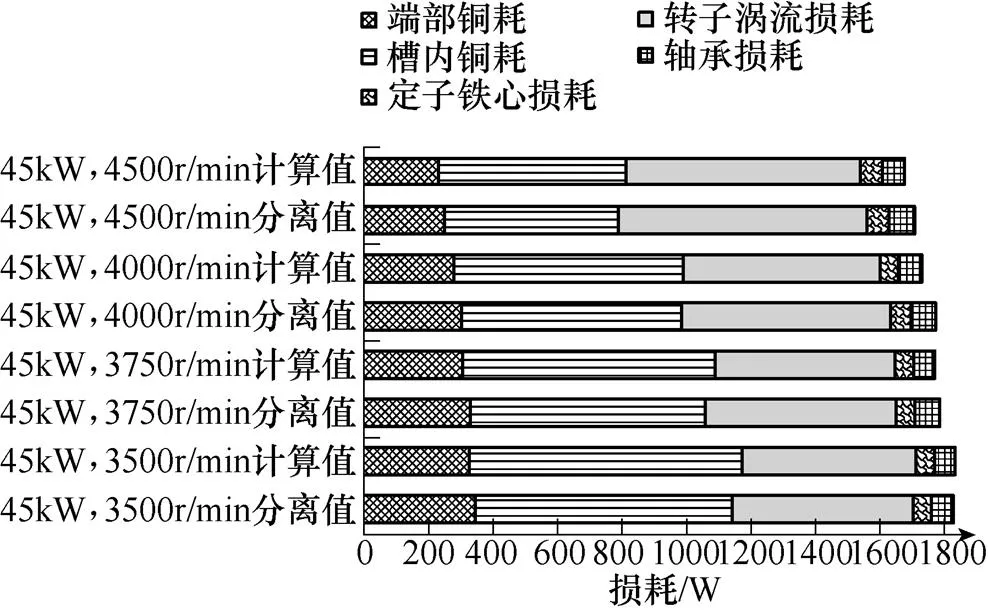
图16 45kW下不同工况的分离结果与计算结果对比
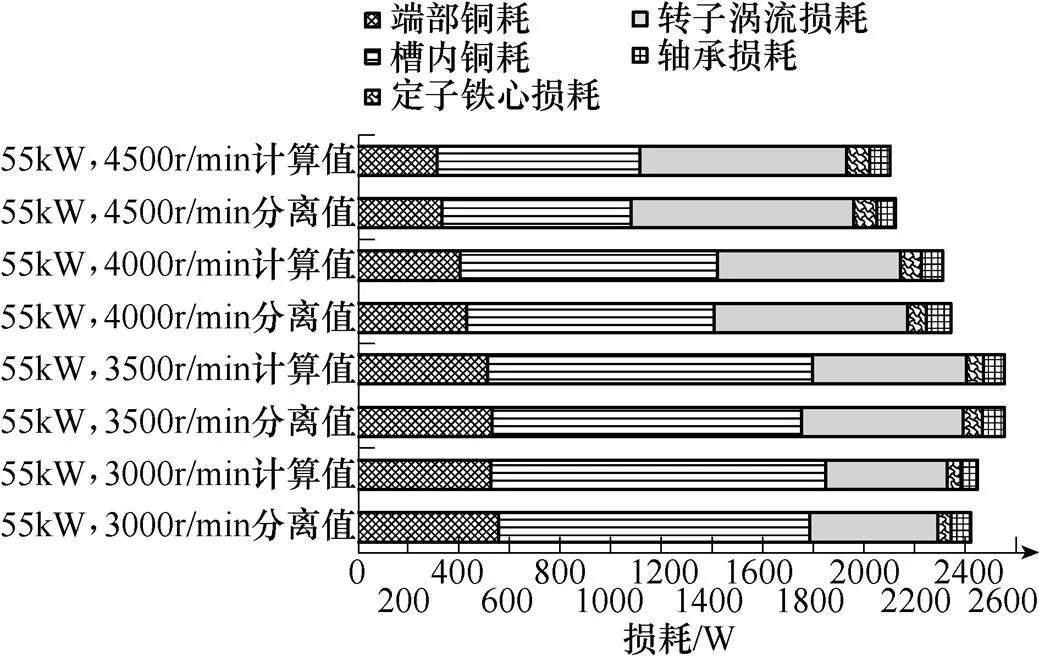
图17 55kW下不同工况的分离结果与计算结果对比
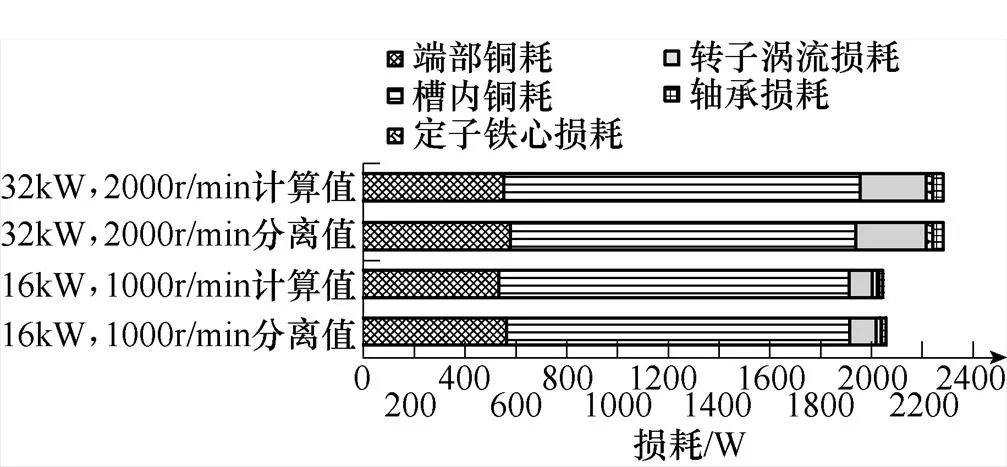
图18 恒扭矩下不同工况的分离结果与计算结果对比
4.2 损耗温度效应验证
同时为了验证损耗模型中的温度效应,对45kW,3 500r/min的工况下,从初始室温开始持续运行。通过对这一工况下的不同温度进行损耗分离,得到不同温度下损耗进行分离与计算值对比结果。对于绕组铜耗的温度效应,温度主要影响绕组阻值,随着温度的升高,绕组阻值不断变大,因此绕组铜耗不断变大。图19为不同绕组温度下绕组铜耗分离值与计算值比较。可以看出,铜耗随着温度的升高而变大。端部绕组铜耗的计算值比分离值小,而槽内绕组铜耗相反,绕组铜耗的分离值与计算值误差在5%左右,通过分析,主要是因为在电机运行过程中端部绕组及槽内绕组温度在LTPN网络中的简化,忽略了绕组本身的温差。槽内绕组计算误差分析主要是由于,实验中槽内绕组温度传感器放置于定子槽孔内,靠近绕组端部。由于槽内绕组与铁心硅钢片较好的热传导以及定子外的强制水冷,造成槽内绕组平均温度比传感器采集的温度要低,从而使槽内绕组铜耗分离值相较计算值低。
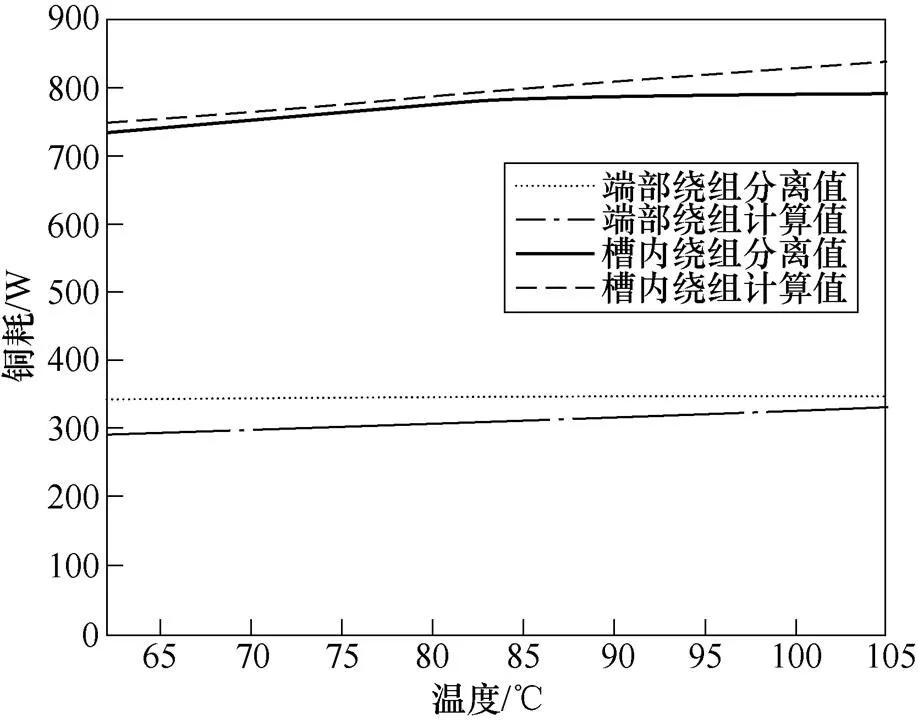
图19 不同绕组温度下绕组铜耗分离值与计算值
对于铁心损耗而言,永磁体温度主要影响电机的磁通密度,随着温度的升高磁通密度会变小,因此铁心损耗也会变小。图20为不同转子温度下定子铁心损耗的分离值与计算值比较。定子铁耗分离值与计算值的误差在3%左右。
永磁体温度的变化会导致永磁体内动态磁通密度变化,从而影响转子涡流损耗。图21为不同转子温度下转子涡流损耗的分离值与计算值比较,分离值与计算值的误差在4%左右。
对于轴承损耗,在实验的工况下轴承的温升在轴承润滑脂正常工作的范围内,因此可以不考虑温度对轴承损耗的影响。

图20 不同转子温度下定子铁心损耗分离值与计算值
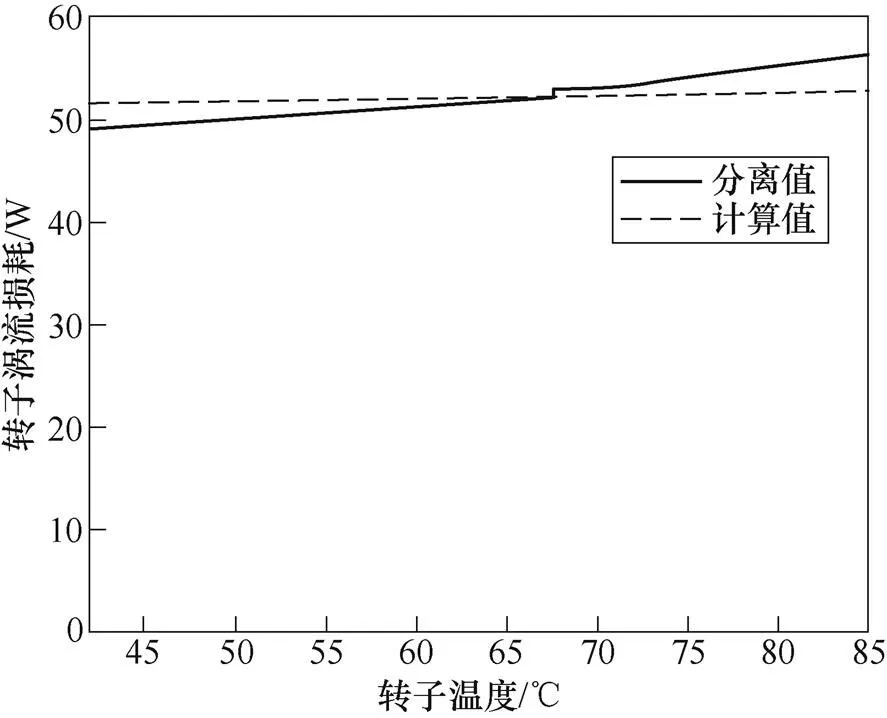
图21 不同转子温度下转子涡流损耗分离值与计算值
5 结论
为了研究永磁电机各部分损耗及实验验证损耗计算结果,本文提出了基于运行参数及温度的损耗模型,以及基于温度实验的永磁电机损耗分离方法。建立5节点浅灰箱电机热网络模型,通过电机温升实验平台采集的温度数据以及热阻和热容输入热网络模型中,利用扩展卡尔曼滤波算法对分离模型进行更新,并分离各部分损耗。
通过分离结果与实测电机总损耗和基于运行参数及温度损耗模型计算结果进行对比分析后,得出永磁电机工况及温度对永磁电机各部分损耗影响较大,在进行损耗模型中需考虑温度的影响。其中,定子铁耗受电机工况及永磁体温度的影响较大,在损耗模型中不能忽略;转子铁耗受永磁电机工况的影响较大,但受各温度影响较小,可忽略;永磁体涡流损耗随着永磁体温度的上升而上升。同时分离得出的各部分损耗与实测值及计算值比较误差较小,能够满足工程需求。表明损耗模型及分离方法的正确性,为永磁电机温度估计和优化提供基础。
[1] 王小飞, 代颖, 罗建. 基于流固耦合的车用永磁同步电机水道设计与温度场分析[J]. 电工技术学报, 2019, 34(增刊1): 22-29.
Wang Xiaofei, Dai Ying, Luo Jian. Waterway design and temperature field analysis of vehicle permanent magnet synchronous motor based on fluid-solid coupling[J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 22-29.
[2] 佟文明, 孙静阳, 吴胜男. 全封闭高速永磁电机转子结构对转子散热的影响[J]. 电工技术学报, 2017, 32(22): 91-100.
Tong Wenming, Sun Jingyang, Wu Shengnan. Effect of rotor structure on rotor dissipation for totally- enclosed high-speed permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 91-100.
[3] 吴柏禧, 万珍平, 张昆, 等. 考虑温度场和流场的永磁同步电机折返型冷却水道设计[J]. 电工技术学报, 2019, 34(11): 2306-2314.
Wu Boxi, Wan Zhenping, Zhang Kun, et al. Design of reentrant cooling channel in permanent magnet synchronous motor considering temperature field and flow field[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2306-2314.
[4] 师蔚, 靳荣华. 基于扩展卡尔曼滤波的永磁电机热网络参数辨识[J]. 电机与控制学报, 2020, 24(12): 106-112.
Shi Wei, Jin Ronghua. Thermal network parameters identification of permanent magnet motor based on extended Kalman filter[J]. Electric Machines and Control, 2020, 24(12): 106-112.
[5] Shi Wei, Zhou Xuan. Online estimation method for permanent magnet temperature of high-density per- manent magnet synchronous motor[J]. IEEJ Transa- ctions on Electrical and Electronic Engineering, 2020, 15(5): 751-756.
[6] 靳荣华, 师蔚. 多因素影响下永磁电机定子铁耗计算[J]. 微特电机, 2019, 47(6): 16-19, 23.
Jin Ronghua, Shi Wei. Calculation of stator iron loss of permanent magnet motor influenced by multi- factors[J]. Small & Special Electrical Machines, 2019, 47(6): 16-19, 23.
[7] Zhang Yue, McLoone S, Cao Wenping. Electro- magnetic loss modeling and demagnetization analysis for high speed permanent magnet machine[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1-5.
[8] 张立军, 徐杰, 孟德建. 基于Preisach模型的永磁同步轮毂电机损耗及温度场建模与分析[J]. 机械工程学报, 2019, 55(22): 33-40, 51.
Zhang Lijun, Xu Jie, Meng Dejian. Modeling and analysis of loss and temperature field in permanent magnet synchronous in-wheel motor based on Preisach theory[J]. Journal of Mechanical Engineering, 2019, 55(22): 33-40, 51.
[9] 朱龙飞, 朱建国, 佟文明, 等. PWM逆变器供电引起的轴向磁通非晶电机谐波损耗的解析计算[J]. 电工技术学报, 2017, 32(16): 115-123.
Zhu Longfei, Zhu Jianguo, Tong Wenming, et al. Analytical calculation of harmonic losses of an axial flux amorphous motor caused by PWM inverter supplying[J]. Transactions of China Electrotechnical Society, 2017, 32(16): 115-123.
[10] 王大朋, 马田. 两种转子结构的永磁无刷直流高速电机转子受力及损耗温度场分析[J]. 电气工程学报, 2018, 13(8): 12-17.
Wang Dapeng, Ma Tian. Loss and temperature field analysis of permanent magnet brushless DC high speed motor with two rotor structures[J]. Journal of Electrical Engineering, 2018, 13(8): 12-17.
[11] 杨江飞, 管华, 杨春华, 等. 负载变化对永磁同步电机性能的影响分析[J]. 电气工程学报, 2018, 13(9): 20-25.
Yang Jiangfei, Guan Hua, Yang Chunhua, et al. Influence of load variation on performance of permanent magnet synchronous motor[J]. Journal of Electrical Engineering, 2018, 13(9): 20-25.
[12] 孙权贵, 邓智泉, 张忠明. 基于齿槽效应的高速永磁电机转子涡流损耗解析计算[J]. 电工技术学报, 2018, 33(9): 1994-2004.
Sun Quangui, Deng Zhiquan, Zhang Zhongming. Analytical calculation of rotor eddy current losses in high speed permanent magnet machines accounting for influence of slot opening[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 1994- 2004.
[13] 朱龙飞, 祝天利, 于慎波, 等. 一种气隙磁导谐波引起的永磁体涡流损耗的解析计算方法[J]. 电机与控制学报, 2020, 24(5): 10-16, 25.
Zhu Longfei, Zhu Tianli, Yu Shenbo, et al. Analytical approach for calculation of eddy current losses in magnets caused by permeance harmonics in air gap[J]. Electric Machines and Control, 2020, 24(5): 10-16, 25.
[14] Sahu R, Pellerey P, Laskaris K. Eddy current loss model unifying the effects of reaction field and non- homogeneous 3-D magnetic field[J]. IEEE Transa- ctions on Magnetics, 2020, 56(2): 1-4.
[15] Koo M M, Choi J Y, Hong K, et al. Comparative analysis of eddy-current loss in permanent magnet synchronous machine considering PM shape and skew effect using 3-D FEA[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.
[16] 陈萍, 唐任远, 佟文明, 等. 高功率密度永磁同步电机永磁体涡流损耗分布规律及其影响[J]. 电工技术学报, 2015, 30(6): 1-9.
Chen Ping, Tang Renyuan, Tong Wenming, et al. Permanent magnet eddy current loss and its influence of high power density permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2015, 30(6): 1-9.
[17] Zhang Peng, Sizov G Y, He Jiangbiao, et al. Calculation of magnet losses in concentrated-winding permanent-magnet synchronous machines using a computationally efficient finite-element method[J]. IEEE Transactions on Industry Applications, 2013, 49(6): 2524-2532.
[18] 朱洒, 卢智鹏, 王卫东, 等. 基于CE-FEA和小信号分析快速计算逆变器供电下聚磁式场调制电机中永磁体涡流损耗[J]. 电工技术学报, 2020, 35(5): 963-971.
Zhu Sa, Lu Zhipeng, Wang Weidong, et al. Fast calculation of PM eddy current loss in FCFMPM machine under PWM VSI supply based on CE-FEA and small-signal analysis[J]. Transactions of China Electrotechnical Society, 2020, 35(5): 963-971.
[19] 张永平, 段小丽, 郭英桂. 永磁同步电动机损耗分离的应用研究[J]. 微特电机, 2016, 44(9): 46-49.
Zhang Yongping, Duan Xiaoli, Guo Yinggui. Research on loss separation of permanent magnet synchronous motor applied in engineering[J]. Small & Special Electrical Machines, 2016, 44(9): 46-49.
[20] Huang Ziyuan, Fang Jiancheng, Liu Xiquan, et al. Loss calculation and thermal analysis of rotors supported by active magnetic bearings for high-speed permanent-magnet electrical machines[J]. IEEE Transactions on Industrial Electronics, 2016, 63(4): 2027-2035.
[21] 王晓远, 刁剑, 王力新, 等. 电动汽车用ISG永磁电机在弱磁条件下的永磁体涡流损耗分析[J]. 机械工程学报, 2020, 56(12): 155-164.
Wang Xiaoyuan, Diao Jian, Wang Lixin, et al. Analysis of the eddy current losses of permanent magnets in permanent magnet synchronous motors for electric vehicles under weak magnetic conditions[J]. Journal of Mechanical Engineering, 2020, 56(12): 155-164.
[22] Yogal N, Lehrmann C, Henke M. Measurement of eddy current loss in permanent magnets with high- frequency effects of electrical machines for hazardous locations[C]//2019 IEEE 22nd International Con- ference on Electrical Machines and Systems (ICEMS), Harbin, China, 2019: 1-5.
[23] 佟文明, 王云学, 贾建国, 等. 变频器供电内置式永磁同步电机转子损耗计算与试验[J]. 电工技术学报, 2018, 33(24): 5811-5820.
Tong Wenming, Wang Yunxue, Jia Jianguo, et al. Calculation and experimental research on the rotor loss of interior permanent magnet synchronous motors with converter supply[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5811-5820.
[24] 李洪宇, 王群京, 李国丽, 等. 基于扩展卡尔曼滤波器的电机参数辨识算法[J]. 电气工程学报, 2015, 10(5): 34-42.
Li Hongyu, Wang Qunjing, Li Guoli, et al. Electro- magnetic parameter identification algorithm of AC motor based on extended Kalman filter[J]. Journal of Electrical Engineering, 2015, 10(5): 34-42.
[25] 刘芳, 马杰, 苏卫星, 等. 基于自适应回归扩展卡尔曼滤波的电动汽车动力电池全生命周期的荷电状态估算方法[J]. 电工技术学报, 2020, 35(4): 698-707.
Liu Fang, Ma Jie, Su Weixing, et al. State of charge estimation method of electric vehicle power battery life cycle based on auto regression extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(4): 698-707.
[26] 宫明辉, 乌江, 焦朝勇. 基于模糊自适应扩展卡尔曼滤波器的锂电池SOC估算方法[J]. 电工技术学报, 2020, 35(18): 3972-3978.
Gong Minghui, Wu Jiang, Jiao Chaoyong. SOC estimation method of lithium battery based on fuzzy adaptive extended Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(18): 3972- 3978.
[27] 潘海鸿, 吕治强, 李君子, 等. 基于灰色扩展卡尔曼滤波的锂离子电池荷电状态估算[J]. 电工技术学报, 2017, 32(21): 1-8.
Pan Haihong, Lü Zhiqiang, Li Junzi, et al. Estimation of lithium-ion battery state of charge based on grey prediction model-extended Kalman filter[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(21): 1-8.
Method of Loss Separation of Permanent Magnet Synchronous Motor Based on Temperature Experiment
112
(1. College of Urban Rail Transit Shanghai University of Engineering Science Shanghai 201620 China 2. Shanghai Electric Drive Co. Ltd Shanghai 201806 China)
In order to study the loss of each part of the permanent magnet synchronous motor (PMSM) under different working conditions and different temperatures, firstly, the losses of the PMSM are simulated based on the operating parameters and temperature, and the loss models are established. The temperature measuring components are embedded in each part of the stator and rotor of the PMSM, and the temperature and loss experiments of the PMSM are carried out by adopting the temperature test of variable working conditions. The equivalent thermal network model of the PMSM is established based on the heat conduction characteristics of the PMSM and the arrangement of the temperature measuring components. According to the results of temperature and total loss of the PMSM under different working conditions, the various losses of the thermal network model are calculated using the extended Kalman filter algorithm. Finally, the separated losses are analyzed and compared with the measured total loss and the calculated loss results to verify the correctness of the separation method and the loss model based on working conditions and temperature.
Permanent magnet synchronous motor, thermal network, extended Kalman filter, temperature experiment, loss separation
10.19595/j.cnki.1000-6753.tces.210332
TM351
国家“十三五”科技部重研发计划资助项目(2016YFB0100700)。
2021-03-12
2021-04-23
骆凯传 男,1996年生,硕士研究生,研究方向永磁电机损耗计算及温度估计。E-mail: 531370502@qq.com
师 蔚 女,1981年生,博士,副教授,硕士生导师,研究方向为永磁电机及其控制技术。E-mail: cane914@126.com(通信作者)
(编辑 崔文静)

