计及用户类型的电能质量区间评估方法

周宇鑫，石晶，陈红坤，丁同，夏渝昆

（1.武汉大学电气与自动化学院，武汉 430072；2.国网武汉市东湖新技术开发区供电公司，武汉 430000）

0 引言

随着电力电子技术的进步，含可再生能源的分布式发电系统高速发展，非线性、冲击性及波动性负荷的比例逐渐增加，使得电力系统遭受的电能质量污染日益严重[1-2]。由于电力企业希望提升运营效益，电力用户也十分注重自身的用电体验，所以电能质量逐渐成为供用电双方广泛关注的焦点[3]。对电能质量进行全面、合理的综合评估，既能帮助电力部门掌握电网电能质量的优劣程度，指导电能质量治理工作的有效开展，也能帮助用户更加了解电能商品的质量情况，为按质计价提供理论支持，促进电力市场的公平交易。因此，进行电能质量综合评估具有重要意义。

现有电能质量评估方法主要分为基于指标特性、权重分析和模型建构等几类[4]。在指标特性方面，文献[5]提出一种集对分析与可变模糊集的分析方法，利用集对分析法确定评估样本与指标标准等级的联系度，结合可变模糊集思想量化两者的隶属关系。文献[6]提出一种基于概率统计的方法，利用各项指标所处等级的概率去确定电能质量等级。在权重分析方面，主要通过对各项电能质量指标进行赋权，包括主观赋权法[7-10]，客观赋权法[11-12]及组合赋权法[13-15]等。在模型建构方面，文献[16]提出一种基于共轭梯度反向传播的、鲁棒性与适应性较强的人工神经网络进行实时的电能质量评估模型。文献[17]使用基于物元可拓理论的电能质量评价模型评价电能质量。上述方法对电能质量评估工作做出了重要贡献，为后续研究提供了宝贵参考。

然而，上述方法大多只根据单个测量点的电能质量数据进行综合评估，未考虑空间域电能质量的整体情况。现代电网中，各项电能质量指标均在时间域和空间域中体现出明显的随机性和波动性，单点采样数据不足以全面反映该项指标的时空变化趋势。此外，现有方法较少考虑不同类型用户的需求差异。在现行电力市场运行机制下，用户的不同响应信息对于电能质量的评估愈发重要。不同类型用户对电能质量有不同的需求，对各项指标的重视程度也存在差异，从而会根据自身偏好对电能质量优劣作出评价。忽视用户需求差异的评估结果往往缺乏合理性和参考价值。

为了解决上述问题，本文提出一种考虑用户类型的电能质量区间评估方法。首先利用区间数描述电能质量稳态与暂态指标。然后在考虑用户需求差异的基础上计算各项指标的主观权重，利用区间数据的变化情况以及指标的冲突性计算客观权重，根据博弈论的思想求解最优组合权重。最后，利用马田-TOPSIS 系统针对不同用户的多区域电能质量优劣程度进行排序，并通过实际算例分析验证了所提评估方法的有效性。

1 电能质量评估指标及数据描述

1.1 电能质量评估指标体系

电能质量指标包括稳态指标和暂态指标。其中稳态指标属于连续型指标，在空间及时间上不断变化；暂态指标属于事件型指标，发生频率具有偶然性，后果较严重[18]。现有评估方法大多将这两类指标分开考虑。但是，实际电网中连续型与事件型的电能质量问题往往同时存在，无论是只考虑稳态指标还是只考虑暂态指标，得到的评估结果都缺乏完整性。鉴于此，为了对电能质量作出更加全面、科学的评估，本文将稳态指标与暂态指标相统一。对于连续型电能质量问题，每一类问题选取一个对应的典型指标，可以较好地反映该类问题的特征；对于电压暂降这一事件型电能质量问题，由于其具有暂降幅值与暂降时间这两个典型特征参数，只选取其中任意一个参数都无法完备地描述电压暂降的特征，因此，对电压暂降问题，选取电压暂降幅值与电压暂降时间这两个指标进行描述。建立如图1 所示的电能质量综合评估指标体系。

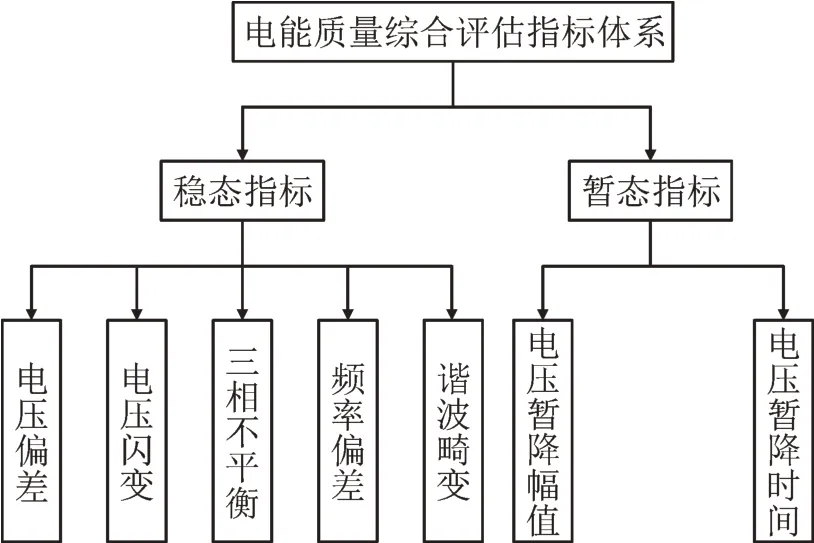
图1 电能质量综合评估指标体系Fig.1 Power quality comprehensive evaluation index system

1.2 电能质量指标数据描述

对于稳态指标而言，在时空域内，各项数据均体现出显著的动态特性。若采用一个确定值对其进行描述，显然不够准确，难以刻画其波动性与不确定性。而对于电压暂降的幅值与时间这两个暂态指标而言，由于其具有事件型的特点，以某一个时间断面的数据作为代表也较为片面。因此，为了刻画各项电能质量指标在时空域内的总体特征，同时避免传统单点评估的不足之处，本文采用区间数对各项指标数据进行描述。与确定数相比，区间数能够体现数据的变化范围，从而更好地反映时空域内电能质量的整体情况。

2 指标权重的确定

2.1 计及用户类型的主观权重

2.1.1 用户对指标的评价流程

不同类型的用户会根据自己的实际情况对电能质量指标提出具体要求。但用户对于指标要求的语言不会达到诸如国标要求那样的准确。为了实现用户对电能质量需求的精细化响应，本文选择指标排序的方式来描述用户需求信息。各类用户根据自身特征，按照对电能质量的偏好程度，对各项评估指标进行排序。顺位越靠前，代表对该项指标越重视。根据排序顺序，不同电能质量敏感类型的用户可以将自己要求较高的某些指标赋予较大的权重，使评估结果更加符合用户的要求，对电力用户选择不同品质的电能提供更加真实可靠的依据。

2.1.2 改进的层次分析法

在用户给出自己的排序顺序后，利用层次分析法计算考虑用户类型的主观权重。由于传统的分析方法利用九标度法进行判断，并且对于判断矩阵有着很严格的要求，必须要通过一致性检验，这就显得十分繁杂。为了避免九标度法过强的主观性，避免繁杂的一致性检验操作，本文采用改进层次分析法[12]进行主观赋权。该方法将九标度改为三标度，并利用拟最优一致矩阵避免一致性检验工作。其原理为：

1）根据指标的排序顺序进行两两比较，得到对应的标度值。为了充分考虑用户对各项电能质量指标的不同要求，标度值的选取见表1。

表1 标度值及其含义Table 1 Scale value and its meaning

2）通过标度值建立比较矩阵R=(rij)m×m，其中，m表示电能质量综合评估指标的个数，rij为比较矩阵R第i行第j列的元素。

3）根据式（1）计算重要性排序指标ki，并根据式（2）构造判断矩阵B。

式中：kmax为ki的最大值；kmin为ki的最小值；bij为判断矩阵B第i行第j列的元素。

4）根据式（3）构造传递矩阵C。

式中，cij为传递矩阵C第i行第j列的元素。5）根据式（4）构造最优传递矩阵D。

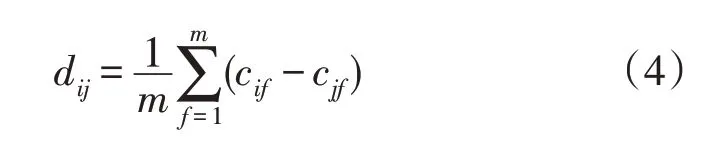
式中，dij为最优传递矩阵D第i行第j列的元素。6）根据式（5）构造拟最优一致矩阵B′。

7）最后，求出拟最优一致矩阵B′最大特征值所对应的特征向量，将其归一化后即可得到指标的主观权重向量。

式中，ωm为第m个指标的主观权重。

2.2 基于改进的区间CRITIC赋权法的客观权重

客观赋权法可以根据各项指标原始数据段波动特征，对其进行相应的赋权，具有很好的客观性。为了同时考虑指标数据的变化情况以及各项指标之间的冲突性，本文利用改进的区间CRITIC赋权法[20]进行客观权重的计算。该方法将原始指标的区间数据规范化，用变异系数代替标准差去体现数据的变异情况，消除了标准差带有量纲的影响。同时，考虑到用相关系数来表示指标之间的冲突性时会出现值为负的情况，因此，在计算时将相关系数取绝对值，这样能够避免负号带来的影响，使结果更加真实可靠。步骤如下：

1）根据实测的区间数据构造原始数据矩阵。

2）数据规范化。

由于本文所选取的电能质量各项指标均是越小越好，属于成本性指标，其规范化公式为

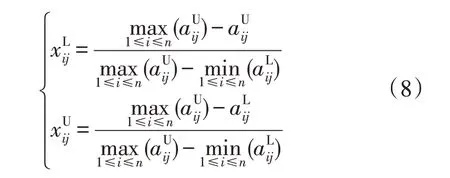
3）计算各项指标的平均值、标准差以及变异系数。

平均值为

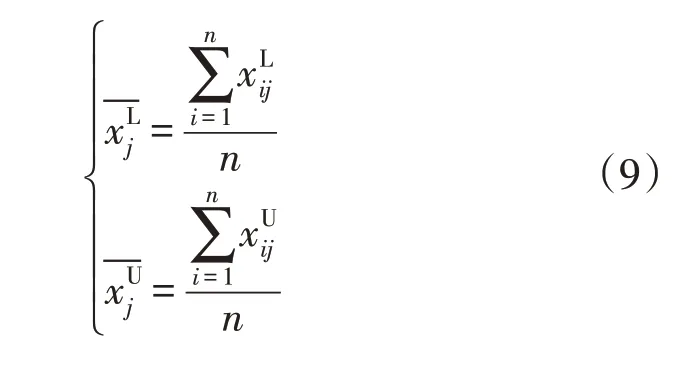
标准差为

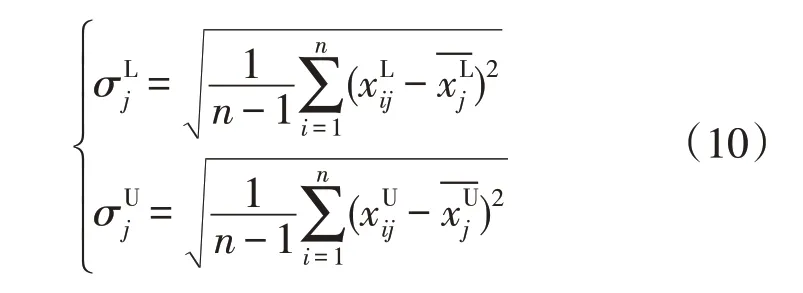
变异系数为

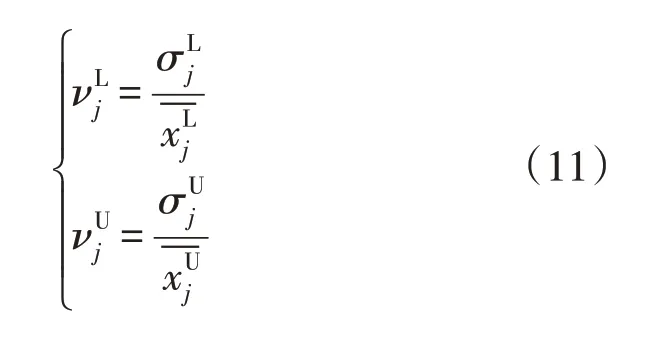
4）计算相关系数。

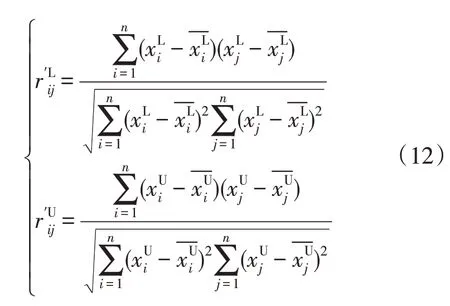
5）计算客观权重。

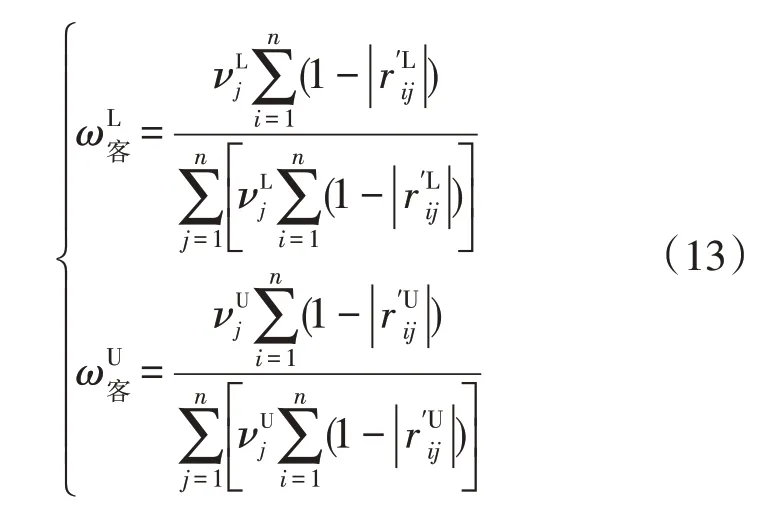
则客观权重为

2.3 基于博弈论求解组合权重

博弈论可以缩小主客观权重之间的偏差，寻找二者之间最优的线性组合，得到一个准确性较高的组合权重。其实现步骤如下[21-22]：

1）计算组合权重ω组。

式中：n为赋权方法个数；si为赋权方法所得权重的系数。

2）最优组合。

构造如下的目标函数，使ω组和ωi离差极小化。

3）最优化一阶导数条件。

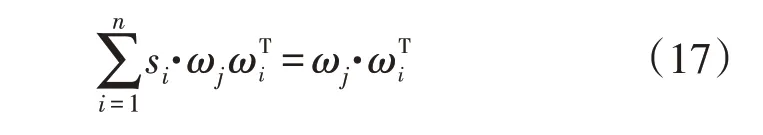
4）计算最优组合权重。

将最优的权重系数si进行规范化处理为

最优组合权重为

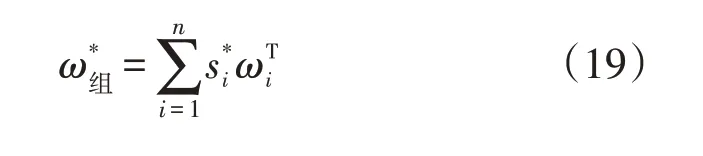
3 马田系统-TOPSIS综合评估方法

3.1 马田系统处理区间向量

目前，针对区间数排序问题，大致可分为两类解决方法[23]：第1 类是通过相关的数学公式，直接将两个区间数进行比较，如可能度矩阵法以及优势度法等。第2 类是将区间数转换为确定数，再根据到正负理想解的距离来进行排序操作，如TOPSIS 法、相对隶属度法等。但是，根据区间数的上下限来决定排名以及用确定的数来代替区间数均不能够真实准确地反映区间数所包含的信息，这样的处理必然会丢失相关信息，造成结果有误。因此本文采用马田系统来处理区间数[24-26]，其主要内容如下:

1）构造正交表。

正交表是用少量的实验来达到获取较全面信息目的的一套综合规范表格。正交表记为。其中，q为实验次数，α表示因素个数，t表示因素的水平个数，即一个因素含有的不同表征种类个数。在马田系统中，t取2 以达到降维目的。利用正交表可以选择较少的试验次数，见表2，3 个因素若是要全部实验需要8 次，而正交表则只需要4 次实验，也即在超长方体上均匀取多个点，以此作为决策信息。因此，正交表可以起到降维的作用，降低区间数信息的丢失。

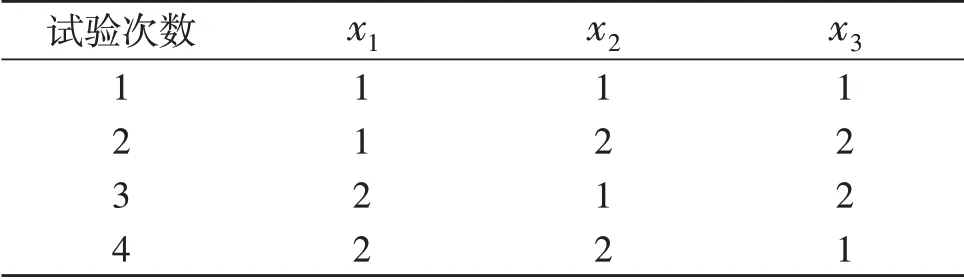
表2 L4( 23 )正交表Table 2 L4( 23 )orthogonal arrays

图2 也从空间上说明了正交表的原理，对于3个因素而言，在超长方体上均匀取A、B、C 和D 这4个分散点即可提高去除多余的实验，提高参与实验变量的优化。

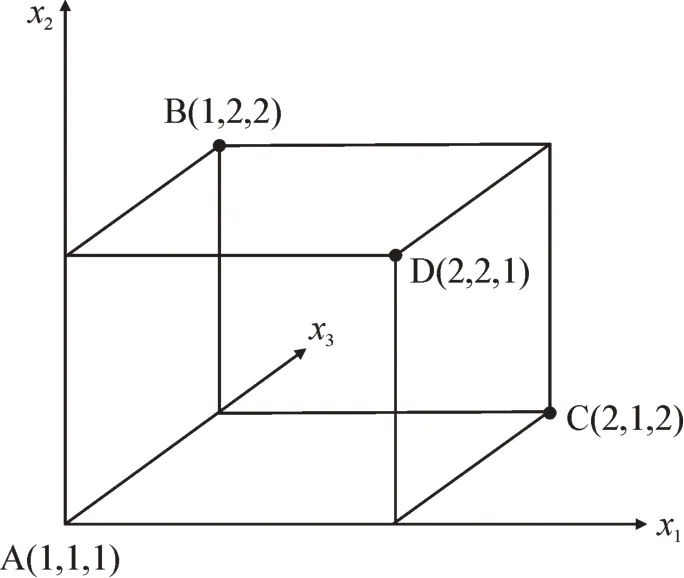
图2 L4( 23 )正交表Fig.2 L4( 23 )orthogonal arrays

2）马氏距离。

由于传统的TOPSIS 排序方法中采用的是欧氏距离，而欧氏距离不考虑指标之间的相关性，会产生模糊的决策结果，产生“逆序”等问题。所以，欧氏距离会因为电能质量指标间的线性关系而失效。因此，利用马氏距离来替代传统的欧氏距离，他不仅考虑指标间的相关性，有着更有效的决策信息表示能力，而且不受量纲的影响。

样品b 到总体A的平方马氏距离定义为

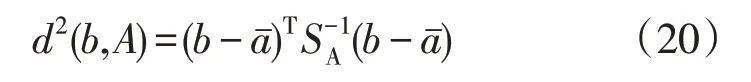
式中：aˉ为总体A的均值向量；SA为总体A的协方差矩阵。

但是，当SA的行列式为0，即其奇异时，上式失效。因此，在这种情况下重新定义马氏距离为

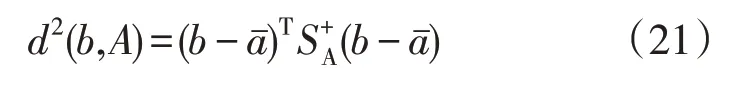
3）信噪比。

望小信噪比定义为

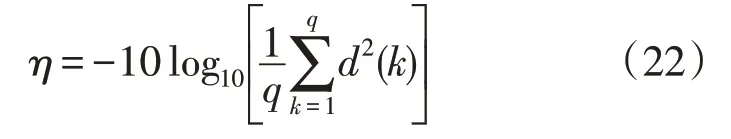
利用信噪比作为衡量指标代替传统的欧氏距离去求得决策方案与正、负理想解的贴近距离，可以保证决策信息的有效性，不会因为指标间的相关性造成干扰。

设样品中的m维区间向量b和总体A中的m维区间向量a在正交实验下得到的布点集分别为

则样品中的m维区间向量b和总体A中的m维区间向量a的望小信噪比定义为

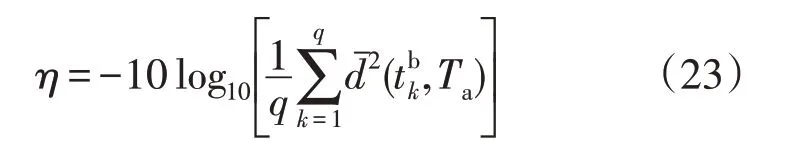
式中，

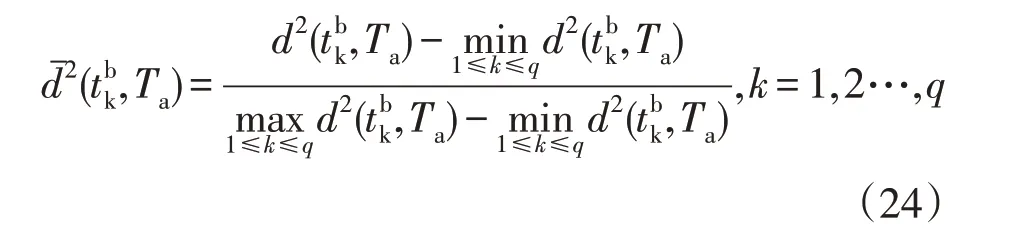
3.2 TOPSIS排序

设有n个不同的选择方案I={I1,I2,…,In}，每一个方案的评价指标有m个，J={J1,J2,…,Jm}。对规范化后的区间数矩阵X进行加权处理后得到加权规范化矩阵Y。区间数的正、负理想解定义为

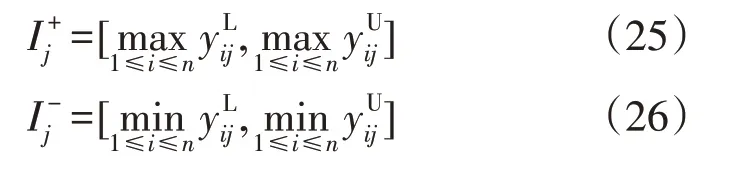
则决策方案与正、负理想方案的望小信噪比定义为

定义γi为方案i与正理想方案的相对贴近度为

方案i的相对贴近度越大，说明方案i与正理想方案越接近，方案i就越优，排名也就越靠前。

3.3 评估方法流程

本文所提电能质量综合评估方法流程见图3，具体步骤如下：

图3 电能质量区间评估流程Fig.3 Power quality interval assessment process

1）采集各项电能质量指标数据并利用区间数进行描述，建立电能质量指标原始区间数据矩阵A。

2）根据式（1）-（6）计算针对不同类型用户的各项指标主观权重向量。

3）根据式（8）-（14）计算电能质量指标区间数据的客观权重向量。

4）根据式（15）-（19）利用博弈论计算各项指标的组合权重向量。

5）利用马田系统构造电能质量指标正交表，计算每个布点集中的布点到正负理想方案的马氏距离。

6）根据式（27）-（29）利用TOPSIS 计算望小信噪比以及相对贴近度，得出电能质量优劣排序结果。

4 算例分析

为了验证本文所提评估方法的有效性，选择4 个不同区域的电能质量监测数据进行评估。采集数据时长为半年，用区间数描述所关注的时空域内各项电能质量指标数据，构造原始区间数据矩阵，见表3。针对每个区域，分别考虑四种不同类型电力用户的需求差异，对各区域的电能质量优劣情况进行排序[27]。

表3 电能质量指标原始区间数据Table 3 Power quality index raw interval data

4.1 电能质量综合评估结果

4.1.1 权重计算结果

首先，根据不同用户的电能质量需求差异，对各项指标的重要性进行排序。排序情况见表4。其中，A 类用户属于电压暂降敏感型用户，对于电压暂降幅值与电压暂降时间这两项指标尤为看重。B 类用户属于电动机类用户，对于三相不平衡以及谐波畸变要求更高。C 类用户对于电压的相关指标有明显的偏重，而D 类用户没有明显的要求，认为各项指标同样重要。

表4 不同类型用户的电能质量指标重要性排序Table 4 Importance rankingof power quality indicators for different types of users

根据式（1）-（6）计算4 种不同类型用户的电能质量指标主观权重，见表5。

表5 不同类型用户的电能质量指标的主观权重Table 5 Subjective weights of power quality indicators for different types of users

然后，利用改进CRITIC 区间赋权法计算客观权重。根据式（8）-（14）计算出各项指标客观权重为ω客=（0.312，0.177，0.057，0.136，0.086，0.108，0.125）。

最后，利用式（15）-（19）计算出每个用户的组合权重，见表6。

表6 不同类型用户的电能质量指标的组合权重Table 6 Combination weights of power quality indicators for different types of users

4.1.2 综合评估结果

将规范化后的区间数据矩阵X与用户权重向量相乘得到加权后的规范化区间数据矩阵Y。由于有7 个评价指标，因此选择L8(27)正交表，见表7。

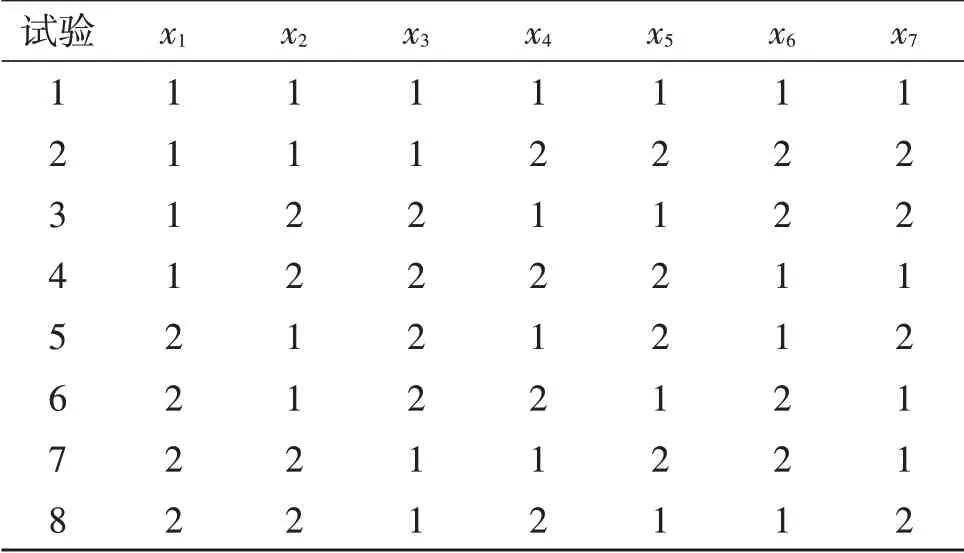
表7 L8( 27 )正交表Table 7 L8( 27 )orthogonal arrays

1 代表取电能质量指标区间数的下限，2 代表取电能质量指标区间数的上限。根据正交表，分别求出4 个数据采集点以及正、负理想方案的布点集。然后求出4 个数据采集点的每个布点到正、负理想方案的马氏距离，计算出望小信噪比，最后得到不同用户中4 个区域的相对贴近度，见表8。

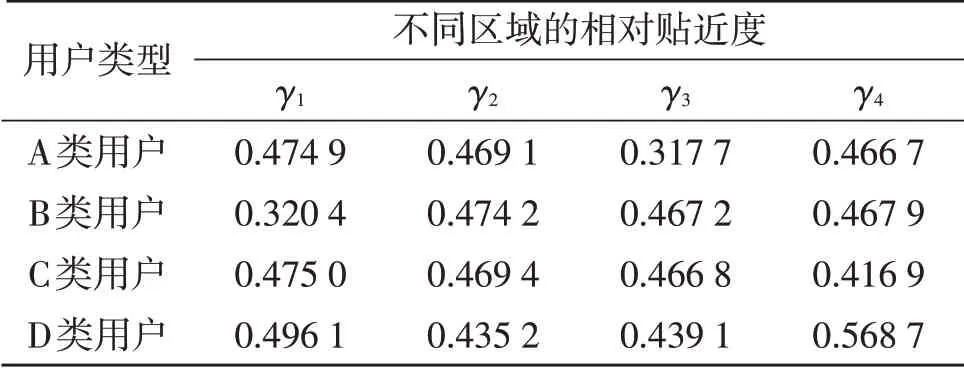
表8 不同用户的相对贴近度Table 8 Relative closeness of different users

由此对不同区域的电能质量优劣情况进行排序，如下所示：

A 类用户：区域1＞区域2＞区域4＞区域3

B 类用户：区域2＞区域4＞区域3＞区域1

C 类用户：区域1＞区域2＞区域3＞区域4

D 类用户：区域4＞区域1＞区域3＞区域2

由于A 类用户对电压暂降相关指标较为敏感，因此，电压暂降幅值与时间波动范围较大的区域3排名最后，而区域1 最优。B 类用户对于三相不平衡和谐波畸变有较高的要求，因此，这两项指标最劣的区域1 排名最后，而区域2 排名最好。同样的，C 类用户对于与电压相关的指标都有更高的需求，因此，4 项电压指标都较差的区域4 排名最后，而区域1 电能质量对于C 类用户而言最好。所以，从最终的结果中可以看出，本文提出的考虑用户类型的电能质量区间评估方法具有科学性与有效性。

4.2 与不考虑用户类型的方法对比

若评估过程中不考虑用户对某些电能质量指标的特殊要求，以C 类用户为例，对比结果见表9。

表9 针对C类用户的不同方法对比Table 9 Comparison of different methods for user C

不考虑用户类型的评估方法所得结果和D 类用户一样，认为区域4 的电能质量是最优的。但是，从结果中可以看出，对于电压指标比较看重的C类用户认为区域4 的电能质量是最劣的。这是因为区域4 虽然比其他指标变化趋势均较平稳，但是其电压偏差幅值大，电压闪变波动较大，对电压相关指标赋予更高权重的C 类用户会更倾向于选择电压指标较好的区域1，所以C 类用户认为区域1 电能质量最优，而区域4 电能质量最劣。由此可见，若在评估过程中忽略用户需求的影响，最终的评估结果会和用户所期望的结果有所偏差，不易与用户达成共识。

4.3 与单点评估的方法对比

针对目前大部分文献中的单点评估方法，以D类用户为例，若随机取区间数据内的某个值进行评估，不管是取区间数的上下限还是95%概率大值，取值不同，则相应的客观权重也会不同，评估模型也会不同，最终会导致排序结果有误差，最终的排序结果与本文方法对比见表10。

表10 针对D类用户的不同方法对比Table 10 Comparison of different methods for user D

可以看出，不考虑区间数的方法对于排序结果有明显影响。若不考虑电能质量指标在时空域内的波动特征，所得到的评估结果具有很大的不确定性。

5 结语

本文提出一种考虑用户类型的电能质量区间评估方法。建立含稳态指标与暂态指标的电能质量综合评估指标体系，并采用区间数对各项指标数据进行统一描述，保证了评估体系的完整性，且体现了电能质量数据在时间域和空间域中的动态特征。在权重分析中，考虑各类用户对电能质量的需求差异造成的影响，计算针对不同用户的相应指标主观权重。根据电能质量指标的冲突性以及数据变化情况计算相应的客观权重，再基于博弈论思想求出组合权重。利用马田-TOPSIS 系统对电能质量优劣程度进行排序。算例分析结果表明，该评估方法充分考虑了用户电能质量需求差异对评估结果的影响，同时有效避免了传统评估方法中取单点进行评估的缺陷，能够实现时空域内科学、合理的电能质量综合评估。