基于直接计数法的船舶横甩发生概率估计探究
曲德才 于立伟 王树青 马 宁
(1.中国海洋大学 山东省海洋工程重点实验室 青岛 266101; 2.上海交通大学 国家重点海洋工程实验室 上海 200030)
0 引 言
恶劣的尾随浪中,在螺旋桨推力、阻力和波浪力的共同作用下会存在船舶纵荡运动的平衡点。在一定的波浪和初始条件下,船舶可能处于波谷附近的稳定平衡点,此时船速加速到波速,这被称为“骑浪”。骑浪普遍被认为是横甩的先决条件,而横甩会导致不可控的大幅艏摇和横摇,甚至造成船舶倾覆。
骑浪横甩运动作为一种强非线性现象,其在不规则波中的概率统计分析无法适用线性叠加原理。GRIM最早开展了不规则尾随浪下骑浪运动的概率统计研究,并将骑浪的发生与航速超过临界速度的增速现象联系在一起。UMEDA基于规则波中确定性骑浪的临界值和波高/周期联合概率分布,提出了一种直接的理论方法,来估计不规则波中的骑浪概率。UMEDA等进一步将这种方法应用于不规则波中横甩的概率估计,并通过蒙特卡罗法验证。该方法采用了规则波中横甩的确定性阈值作为不规则波中的横甩判定条件。然后,UMEDA等开展了不规则波中的自航模实验,以进一步验证所提出的横甩概率估计方法,结果表明横甩概率估计与实验结果的差异处在95%置信区间内。
近年来,受规则波浪中骑浪发生时船速达到波速的现象启发,研究人员提出将不规则波浪中骑浪的发生与船速超过瞬时波速的现象联系起来,这种船速超过瞬时波速的现象称为增速(high run)。这就首先需要阐明不规则波中瞬时波速(也称为局部波速)的物理含义。SPYROU等和BELENKY等提出通过波浪的过零和恒定斜率点的速度来表征局部瞬时波速。同时,SPYROU等和THEMELIS等提出通过希尔伯特变换获得瞬时波速的方法,并对不同的瞬时波速计算方法进行了比较,证明了这些方法的相似性。BELENKY等进一步研究了不规则波中增速的概率统计结果。在此基础上,SPYROU等和THEMILIS等研究了横甩概率及其与增速的相关性。通过对大量数值模拟的直接计数,拟合了增速和显著艏摇累积时间直方图,研究了横摇对增速横甩相关性的影响,并对航向、舵控制增益以及运动阈值进行了灵敏度研究。由此可见,对增速现象的研究有助于骑浪和横甩发生概率的研究,而随着IMO二代完整稳性衡准的发布试用,不规则波中骑浪和横甩发生概率的研究至关重要。
因此,本文针对不规则波中的骑浪/横甩稳性失效模式开展研究,以ITTC A2拖网渔船为例,采用了六自由度数值预报模型,选取具有不同航速、浪向、波浪谱截断区域和值工况,进行大量密集重复模拟,再现了船舶发生骑浪/横甩现象的过程。通过使用希尔伯特变换计算的瞬时波速来识别增速状态,定量研究了船舶发生增速、横甩、显著艏摇和横摇的概率,为IMO船舶二代完整稳性衡准的应用提供技术支撑。
1 数学模型
本文中建立了六自由度操纵性运动模型开展不规则波中骑浪/横甩的数值模拟模型,模型中考虑了非线性的回复力和Froude-krylov(F-K)力以及舵力、螺旋桨动力的作用。
1.1 坐标系统
船舶的运动坐标系统中包含3个坐标系:地球坐标系O-xyz、参考坐标系-和船体固定坐标系O-xyz。各坐标系及运动正方向如图1所示。原点被选为船舶重心。
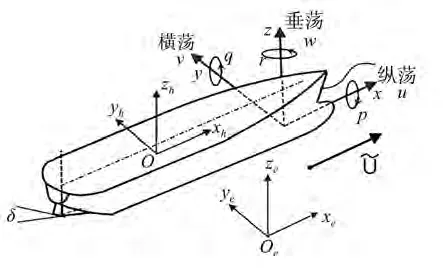
图1 坐标系与运动方向
位置、速度和力矢量定义如下:



式中:、、、、和是地球坐标中的速度;和是变换矩阵。
1.2 6-DOF操纵性运动模型
在六自由度操纵性运动模型中,基于弱耦合理论将横摇、垂荡与纵摇MMG模型和耐波性模型在同一坐标系下进行耦合,如式(3)所示。
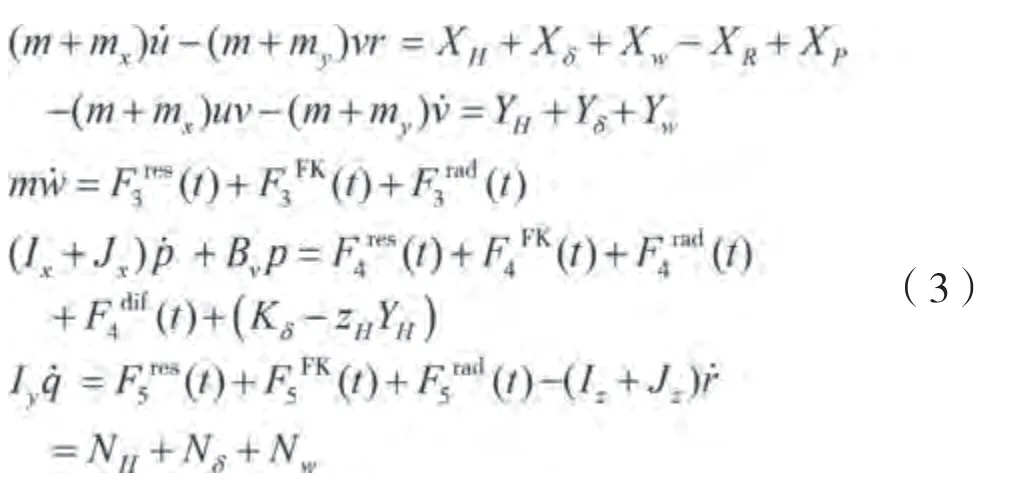
式中:为船舶质量,kg;m为附加质量,kg;I为惯性矩,m;J为附加惯性矩;(X,Y,N)为舵力,kN;X为纵荡波浪力,kN;X为阻力X为螺旋桨推力,kN;B是Ikeda半经验公式估计的横摇粘性阻尼,N·s/m;(X,Y,N)是船体力,kN;z是船体力Y作用点的垂向坐标;F()为非线性回复力,kN;F()为F-K力,kN;F()为辐射;F()为绕射力,kN。各力的计算方法如式(4)所示。

式中:、和是阻力曲线的拟合系数;Y为横荡力,kN;N为摇艏力矩一阶水动力导数;X为纵荡力;Y为横荡力,kN;N为摇艏力矩二阶水动力导数。根据脉冲响应函数(IRF)方法,将切片(STF)法得到的频域结果通过时延函数R和Q转移到时域,得到时域辐射和绕射力F(),F()。由于骑浪时遭遇频率很小,因此在此计算中忽略了垂荡和纵摇运动的绕射力。螺旋桨和舵力的计算方法可参见文献[15]中所示。
1.3 非线性回复力和F-K力
本文通过瞬时湿表面上的压力积分来计算船舶在波浪中所受到的非线性回复力和F-K力。在计算过程中,船体和上层甲板由几个非均匀有理B样条(NURBS)曲面组成,如图2所示。

图2 ITTC A2 渔船船体NURBS曲面
每个曲面的面积为A,在船体固定坐标系下,其形心坐标r=(x,y,z),曲面的法向量n=(,,)。因此,非线性回复力和F-K力的计算公式如下:



式中:吃水d(x,)和波幅()的计算公式如下:

式中:A和A代表规则波和不规则波中的波幅;S()是不规则的波谱;,,,ω分别是波数、浪向角、波频和波遭遇频率;N是波浪谱的离散分量数;θ是随机相位;上标()和()表示船体固定坐标-XYZ和地球坐标O-XYZ中的 矢量。
2 骑浪横甩数值模拟
2.1 船舶参数和计算工况
用于数值模拟的船模是 ITTC A2 渔船。船舶和舵的主尺度如表1所示。
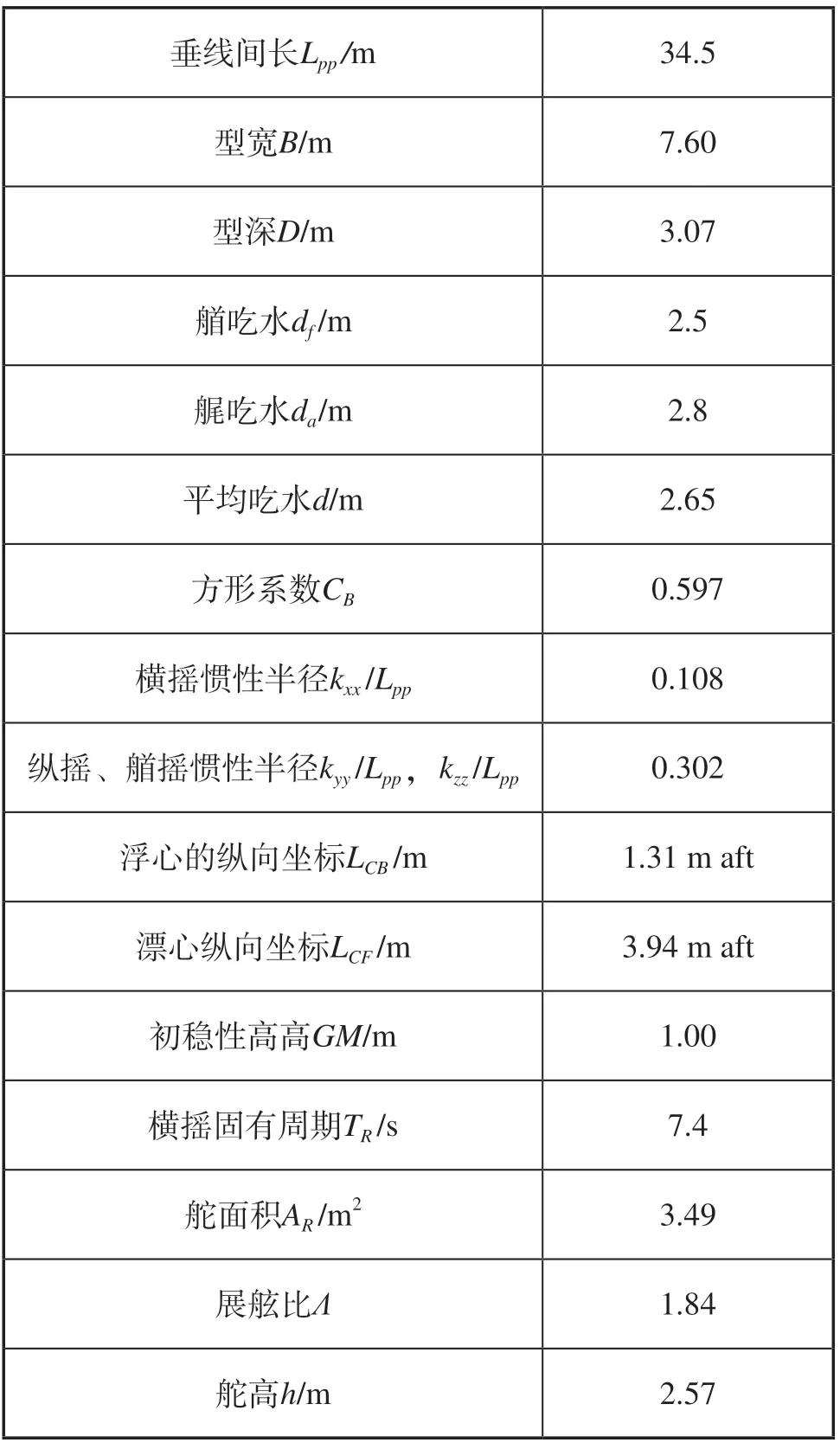
表1 ITTC A2 渔船主尺度
在数值模拟中,采用了JONSWAP波浪谱,其有义波高为H= 2.68 m,谱峰周期T= 5 s,如下页图3所示。在仿真过程中,以Δ=0.004 rad/s的间隔对频率范围进行离散,这样可以获得2π/Δ=1 570 s的不重复仿真时间。不规则波产生的参数如下页表2 所示。

表2 不规则波生成参数

图3 JONSWAP波浪谱与频率范围
在上述不规则波下,选取了具有不同波浪谱截断频率范围、值、标称弗劳德数()和浪向角的工况。对于每个工况,均进行了225次具有不同随机相位的独立重复实现。基于这些密集的重复模拟结果,采用直接计数法来研究不同工况下骑浪、横摇和显著横摇的概率。详细工况设置如表3所示。

表3 计算工况
2.2 瞬时波速的计算
在数值模拟过程中,为了判定不规则波中船速是否达到波速发生骑浪,需要计算不规则波中瞬时波速。本文中基于希尔伯特变换计算瞬时波速,这一方法类似于SPYROU描述的方法,其是使用希尔伯特变换得到瞬时相位,然后计算瞬时相位相对于位置和时间的偏导数,来获得瞬时波速。
对于任意数据序列(),其希尔伯特变换()可以导出为:

式中:..即principal value的缩写,是柯西主值积分;希尔伯特变换被定义为()和1/的卷积积分;()与()的相位差为π/2;此外,希尔伯特变换将真实数据序列传输到复数信号。复数信号定义为:
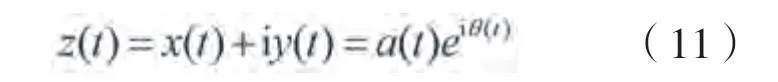
式中:()是瞬时振幅,即包络;()是瞬时相位。

因此,瞬时频率()可以定义为瞬时相位()的导数,如下所示:

将替换为式(10)、(11)和(12)中的,瞬时波数()可以计算如下:

最后,瞬时波速计算如下:

在本研究中,希尔伯特变换是使用快速傅里叶变换(FFT)实现的。
2.3 数值模拟结果
基于第2章中的数值模型,模拟了不同工况下船舶在不规则波中的运动。在每种工况下均进行了225次独立的重复实现。部分运动响应结果如图4~9所示。每个图包含有4个子图,从上到下分别为纵摇与垂荡、横摇、艏摇,以及船速与波速的时历曲线。
图4中,在低情况下,船速达不到波速,几乎未发生骑浪。如图5所示的高下,出现大量航速高于波速的情况。在不规则波下,航速高于波速的状态称为增速,增速现象与骑浪的发生密切相关;同时,在0°浪向角下,横摇和艏摇运动几乎 为0。

图4 Fr=0.3、浪向角为0°工况的模拟结果
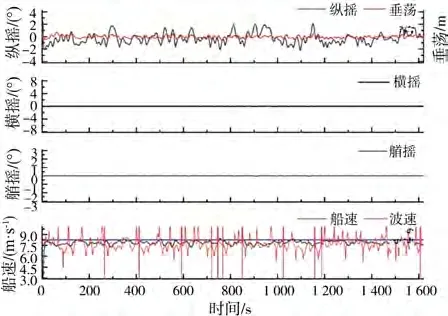
图5 Fr=0.45、浪向角为0°工况的模拟结果
图6~8显示了浪向角30°下的数值模拟结果。当浪向角较大时,可以观察到横摇和艏摇运动的不稳定性。对于某些工况,船舶在经历相对较长的增速后发生倾覆(如图8中的=100 s左右所示),这表明船舶倾覆和增速之间可能存在一定的相关性。在=0.45、浪向角为10°的图9中,横摇和艏摇运动的不稳定性也很明显,在经历较长时间增速后,倾覆发生在=364.74 s左右。
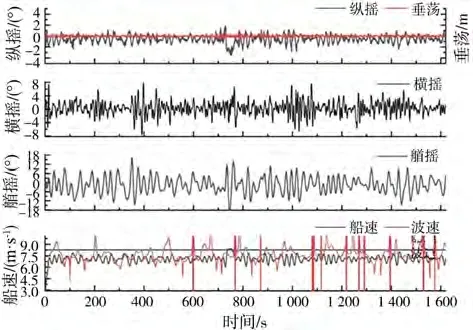
图6 Fr=0.40、浪向角为30°工况的模拟结果

图7 Fr=0.43、浪向角为30°工况的模拟结果
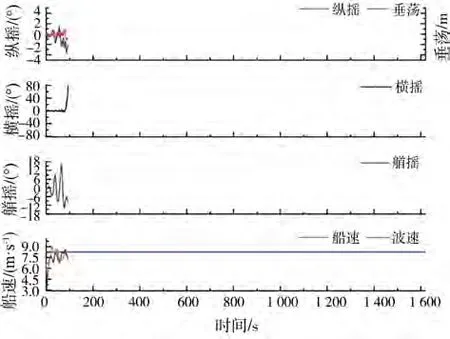
图8 Fr=0.43、浪向角为30°工况的模拟结果,船舶倾覆t =100 s

图9 Fr=0.45、浪向角为10°工况的模拟结果,船舶倾覆t =364 s
3 增速和横甩运动的统计分析
基于第2章中数值模型开展了大量重复数值模拟,本节中采用直接计数方法对数值模拟结果进行分析,开展不规则波下增速和横甩运动的统计评估。首先,根据THEMELIS等的定义,给出了增速、增速后横甩、显著艏摇和显著横摇的阈值和概率的估计方法:
(1)增速现象:当船速超过瞬时波速时,识别出增速发生,船速低于标称时,增速结束。其概率估计为增速的总持续时间与总模拟时间的比值。
(2)增速后横甩:当船舶的航向角超过指令航向±5°并且船舶正在经历增速时,认为其发生增速后横甩。其概率估计值定义为增速后横甩的总持续时间与增速的总持续时间的比值。在分析过程中还计算了总模拟时间内增速后横甩的概率估计值,其定义为增速后横甩的总持续时间与总持续时间的比值。
(3)显著艏摇:当船舶艏摇偏航的绝对值超过5°时,发生显著艏摇。其概率估计值定义为偏航的总持续时间与总模拟时间的比值。
(4)显著横摇:当船舶横摇角的绝对值超过5°和10°时,发生显著横摇。其概率估计值定义为横摇超限的总持续时间与总模拟时间的比值。
3.1 增速现象的概率估计
首先,为了验证独立模拟的数量是否足够,使用式(16)和(17)计算增速概率的标准差随重复实现样本数增加的变化情况。

式中:是同一工况下重复实现样本的数量;x是第个实现的概率估计值;μ为平均值;σ为标准差。0.40、0.45和浪向角=20的结果如图10和下页图11所示。从这两个图中可得,200次模拟后概率的标准差是稳定的。因此,同一工况下独立重复实现的数量足以获得具有统计意义的结果。

图10 Fr=0.40,浪向角为20°,骑浪集成概率的标准差

图11 Fr=0.45,浪向角为20°,骑浪集成概率的标准差
图13~18显示了不同工况下增速的概率估计结果,在这些图中,均采用了箱型图来表示增速的概率估计结果,见图12。
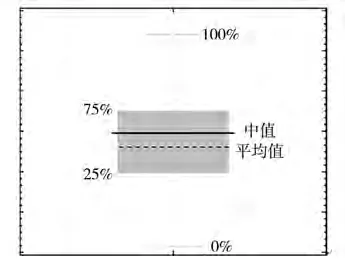
图12 箱型图
根据THEMELIS等,箱型图主要基于4分位数绘制。4分位数定义为将频率分布划分为25%、50%、75%和100%4个部分,如图12所示,概率的中位数和平均值以粗实心和虚线水平线的形式绘于图中。灰色区域下限表示第 1个4分位数的边界,而灰色区域的上限表示第 3个4分位数3的边界。此外,最高和最低的细实心水平线表示与中位数有最大偏差的值。
图13显示了不同下浪向角0°的增速概率估计结果。

图13 浪向角0°时,不同Fr的增速概率统计结果
可以发现:与规则波中的骑浪相似,随着船舶标称的增加,增速的概率也显着增加。因此,在不规则波浪中增速现象的概率与骑浪的概率高度相关。
图14~16显示了每个标称在不同浪向角下增速的概率估计结果。随着标称从=0.30的图14增加到=0.45的图16,所有浪向角的增速概率显著增加。对于每个标称下,不同浪向角的骑浪概率没有显示出很大的差异。在较大的浪向角下,骑浪的可能性往往会降低。
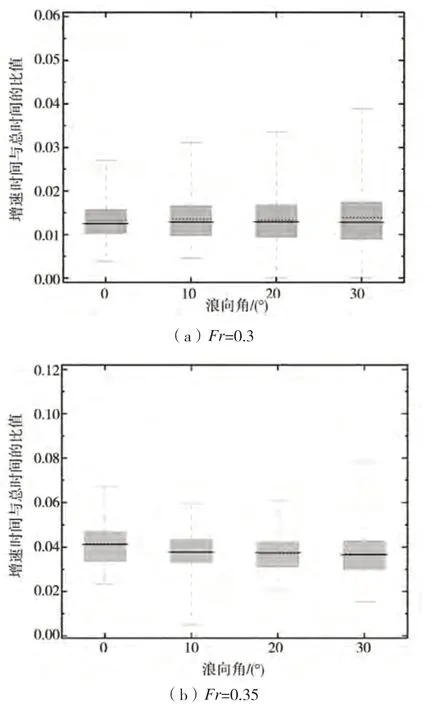
图14 不同浪向角时,Fr=0.3和Fr=0.35时的增速概率统计结果

图16 不同浪向角时,Fr=0.43和Fr=0.45时的增速概率统计结果
下页图17为不同波浪谱截断频率范围下的增速概率统计结果,从图中可以看出,当波浪谱截断频率范围增加到0.9时,增速的概率估计上升。

图17 不同波浪谱截断频率范围下,Fr=0.40和Fr=0.45时的增速概率统计结果

图15 不同浪向角时,Fr=0.38和Fr=0.40时的增速概率统计结果
3.2 增速后横甩的概率估计
图18~20显示了增速后横甩的概率估计。从图中可知,随着浪向角的增加,增速后横甩的概率估计明显增加。因此,可能横甩的概率与浪向角的大小密切相关。当浪向角为10°时,增速中可能横甩的总持续时间随着的增加而缓慢增加。当浪向角在20°时,其值大部分都在10%~25%的范围内。当浪向角达到30°时,增速中可能横甩的概率估计值先增加后降低。对于≥0.38的工况,可能横甩的总持续时间可占增速总时间持续时间的30%~50%。

图18 不同浪向角时,Fr=0.35和Fr=0.38时的增速后横甩统计结果

图19 不同浪向角时,Fr=0.40和Fr=0.43时的增速后横甩统计结果

图20 不同浪向角时,Fr=0.45的增速后横甩统计结果
3.3 显著艏摇的概率评估
图21 ~25显示了不同工况下增速后横甩和显著艏摇的概率估计值。在每个图中,(a)是在总模拟时间内增速后横甩的概率估计,而(b)是显著艏摇的概率估计。首先,造成显著艏摇有2个原因:一是波浪力引起的正常偏航,另一个是骑浪引起的艏摇不稳定。后者被称为横甩。因此,在总模拟时间内,所有增速后横甩事件都包含在艏摇角偏航事件中。也就是说,在总模拟时间(a)中,在增速后横甩的概率估计总是小于显著艏摇(b)的概率估计,这可以从图21~25中观察到。此外,(b)-(a)产生由波浪力引起的正常偏航的概率估计值。
从图21~25中发现,随着的增加,总时间(a)中增速后横甩的概率估计显著增加,而波浪力(b)-(a)诱导的正常偏航运动的概率估计值降低。对于≥0.43,增速后横甩事件可以占显著艏摇角事件的50%~80%,如图24和图25所示。此外,从这些图中可以看出,随浪向角的增加,增速后横甩和显著艏摇的概率估计均增加。

图21 不同浪向角时,Fr=0.35的总时间下,增速后横甩(a)与显著艏摇(b)统计结果
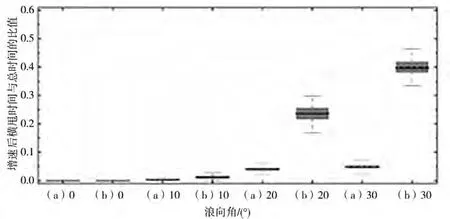
图22 不同浪向角时,Fr=0.38的总时间下,增速后横甩(a)与显著艏摇(b)统计结果

图24 不同浪向角时,Fr=0.43的总时间下,增速后横甩(a)与显著艏摇(b)统计结果

图25 不同浪向角时,Fr=0.45的总时间下,增速后横甩(a)与显著艏摇(b)统计结果

图23 不同浪向角时,Fr=0.40的总时间下,增速后横甩(a)与显著艏摇(b)统计结果
3.4 显著横摇概率评估
显著横摇阈值为10°时不同标称的显著横摇概率估计值如下页图26和图27所示。从中可以观察到,显著横摇概率降低至0.03以下,显著横摇的概率估计值均随浪向角增加而增加,这与增速后横甩的概率变化规律相同。不同值下的显著横摇概率估计值请参见下页图28和下页图29。可见,小值下,显著横摇概率估计值会增加。
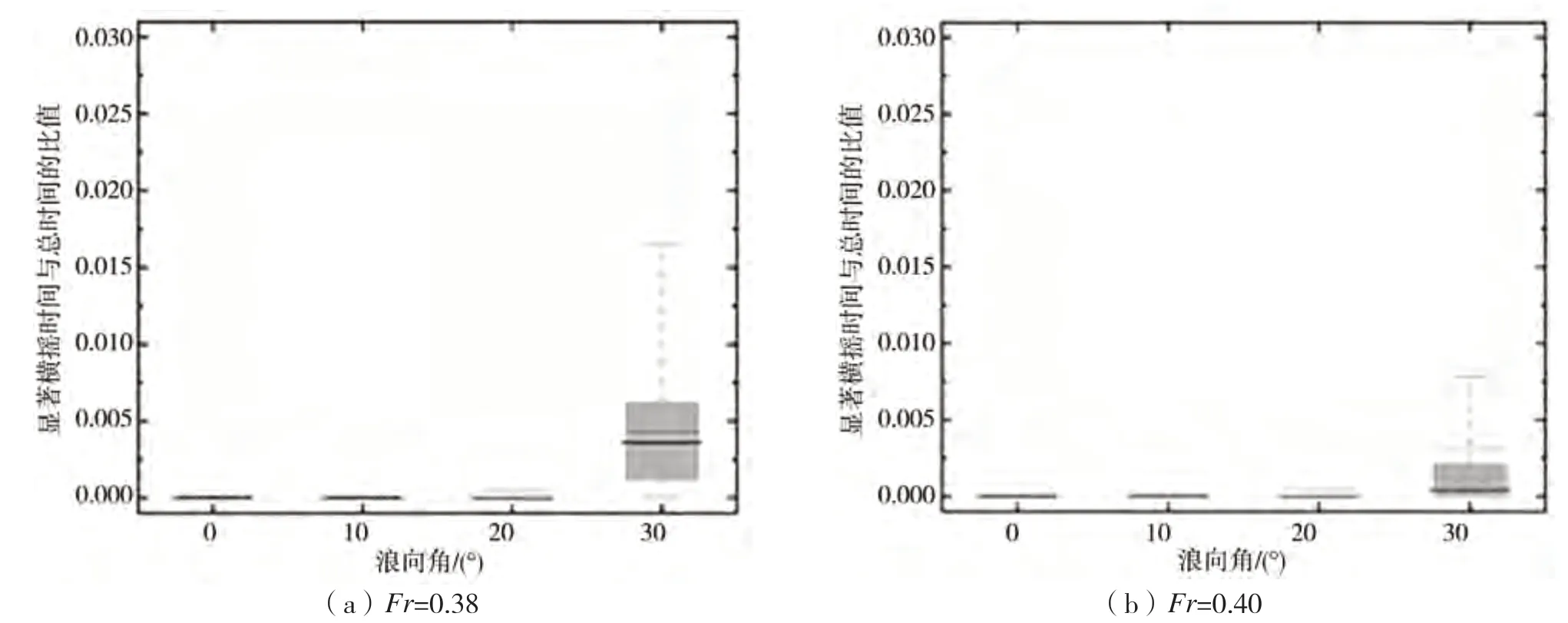
图26 不同浪向角时,Fr=0.38和Fr=0.40时的显著横摇(10°)统计结果

图27 不同浪向角时,Fr=0.43和Fr=0.45时的显著横摇(10°)统计结果
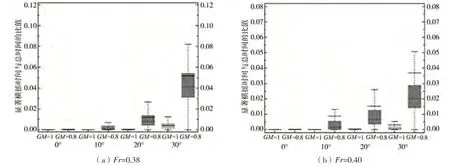
图28 不同GM值时,Fr=0.38和Fr=0.40时的显著横摇(10°)统计结果

图29 不同GM值时,Fr=0.43和Fr=0.45时的显著横摇(10°)统计结果
4 结 论
本研究中,基于不规则波中骑浪横甩六自由度数值预报模型,对不同浪向角、航速、波浪谱截断范围和GM值工况下的船舶骑浪横甩运动进行了密集的数值模拟。然后,在数值模拟结果基础上应用直接计数法,估计了增速、增速后横甩、显著艏摇和显著横摇的概率,并得出以下结论:
(1)使用希尔伯特变换计算的瞬时波速用于识别增速。在不同浪向角下,船舶经历长时间的增速后横甩倾覆,这表明倾覆和增速之间存在相关性。
(2)类似于规则波中的骑浪,增速的概率随着标称的增加而显着增加,可见不规则波中增速与骑浪的发生高度相关。同时,波浪谱频率截断范围对增速的概率估计有较大的影响。
(3)增速后横甩的概率随着浪向角的增加而显著增加。当浪向角达到30°时,横甩的总持续时间可占增速总持续时间的30%~50%,特别是对于高。
(4)显著艏摇包括增速后横甩和波浪力诱导的艏摇2部分;而在高下,在总模拟时间中,增速后横甩事件可以占显著艏摇角事件的50%~80%。
(5)显著横摇的概率估计值均随浪向角增加而增加,这与增速后横甩的概率变化规律相同。

