基于实验修正法的机舱温度场仿真方法研究
王梓宇,彭宇明,黄海波,罗 振
(1.西南交通大学机械工程学院,四川 成都 610031;2.西安交通大学机械学院,陕西 西安 710049;3.柳州龙杰汽车配件有限公司,广西 柳州 545000)
1 引言
在发动机在运行过程中,大部分热量通将过废气经排气管排出,部分热量会传递到排气管上。在热浸工况下其表面温度可高达800℃,隔热罩可以起到隔绝热量散失以达到保护机舱内其他零部件的作用[1]。
但由于机舱内部结构部件的复杂性,导致研究其换热现象变得更加的困难,难以得到准确的温度场分布。目前针对机舱热管理分析所采用的方法主要是实验与仿真相结合,由于实验成本高、周期长,工程上大多采用数值仿真的方式;但在考虑热辐射的情况下,传统的数值仿真占用硬件资源大、效率低。国内外学者采用1D(一维)-3D(三维)和3D-3D 的联合仿真方式[2-3],来提高仿真的效率,但一维仿真属于系统分析,无法获得较为全面的数据;传统的三维耦合仿真消耗资源大,且没有考虑热辐射的影响。
对流换热作为机舱热分析的难点,主要在于对流换热系数的不确定性。文献[4]利用发射率不同的材料,将对流换热热流密度与辐射热流密度分离出来的思想,通过实验测试研究了发动机舱内总热流密度与对流换热密度的关系;文献[5]通过简化发动机舱模型以及内部复杂的零部件,并结合仿真与实验数据对机舱内的温度场进行了研究。
2 传热计算及修正原理
机舱内散热器的散热原理主要是利用流体的流动性,将热量传递到外部环境中。其换热过程主要为对流、热传递以及热辐射,总传热过程的计算如下:

2.1 对流换热相似准则
对流换热系数的计算,目前主要有实验法和相似原理法,工程上大多采用相似原理,1947年,米海耶夫综合了大量的自由运动放热的数据,把横圆柱、平竖壁、竖圆柱和球的数据合并在一起处理,总结得出了适用于不同几何形状物体的准则公式[6]。

式中:g[ m∕s2]—重力加速度;av—气体的体积膨胀系数;Δt[K]—传热温差;l—特征尺寸[ m ];v[ Pa·s ]—运动粘度;tm[K]—特征温度,取介质在边界上的平均温度。针对隔热罩模型,其表面的对流换热系数计算采用米海耶夫公式,其中,tw由实验测得。
2.2 对流换热系数实验修正原理
机舱热分析的难点在于对流换热系数的获取,对流换热系数的影响因素较多。基于相似原理和量纲分析通过实验测量直接或者间接的获取对流换热系数,得到机舱内真实的流动信息,但实验测试所消耗额资源较大,且对于表面较为复杂的模型,采用相似准则误差较大,为此建立实验与仿真相结合的温度场分析方法,通过搭建温度场测试实验台架,为数值仿真提供准确的边界条件,并可通过实验测试结果对仿真结果进行校正,其对换热系数的修正方式如下:
实验测点温度的相对误差为:
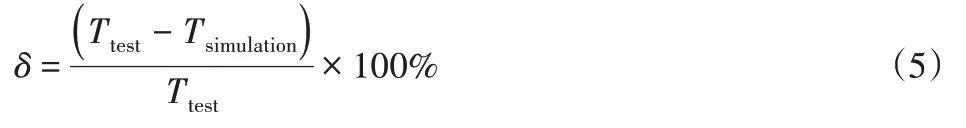
式中:Ttest—实验测试温度;Tsimulation—仿真计算温度。
对流换热系数修正公式:

3 机舱温度场算例分析
针对某车型发动机排气歧管隔热罩,建立简化的发动机舱模型,搭建温度场测试模拟台架实验;建立三维耦合数据仿真模型,利用实验数据修正数值仿真模型,使得仿真数据与实验结果误差较小,验证基于实验数据修正法的数值仿真结果的准确性。
3.1 机舱温度场简易测试平台
发动机舱内流场散热特性实验,主要目的是获取舱内各散热部件散热特性和舱内温度分布特性。针对某车型发动机排气歧管隔热罩,对发动机舱结构进行简化,建立简化的机舱模型,搭建一种适应于多工况下温度场测试的模拟实验台架。
实验台架利用规则几何体代替发动机、蓄电池、水箱等部件。实验台架,如图1所示。本实验台架其热源大小以及机舱内各部件的位置可根据研究对象进行调整,具有多工况的拟合适应性。

图1 发动机舱模拟实验台架Fig.1 Engine Room Simulation Bench
参考GB∕T12542-2009《汽车热平衡能力道路实验方法》相关的内容,进行工况和实验环境设计,实验工况,如表1所示。
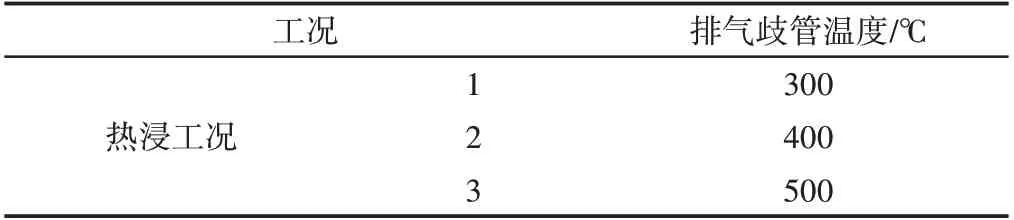
表1 实验测试工况Tab.1 Experimental Test Condition
机舱模型三维模型及其测点布置,如图3所示。在保持测点位置不变的情况下,进行3组热浸工况实验测试,即热源温度为300℃、400℃和500℃,实验测试的时间在5月份左右,实验室环境温度采用温度计标定,室内环境温度在23°左右。隔热罩表面测点及热流场测点布置,如图2所示。测点1-10为隔热罩表面测点,测点11-15位隔热罩前侧流场温度测点。

图2 实验温度测点布置Fig.2 Experimental Temperature Measurement Point Arrangement
3.2 数值仿真计算
对于机舱热管理的数值仿真分析,考虑到机舱内流体的对流换热影响,采用间接耦合的方式,即将流体域和固体域分开计算,通过搭建耦合仿真平台进行数据交换,基于间接耦合,并利用实验测试数据对换热系数进行修正的方式,进行机舱温度场的耦合仿真分析。
3.2.1 耦合计算方法
在仿真计算中,首先进行固体域的计算,设定各部件的热边界条件为对流换热,对流换热系数的指定通过台架实验所的到的测点温度,根据经验公式[6]计算得出的不同部件表面的对流换热系数,环境温度设定为300K,仿真计算机舱内温度场的分布,分析的到的温度场与实验测得温度进行对比,根据仿真结果与实验结果的误差,对换热系数进行修正,计算流程,如图3所示。
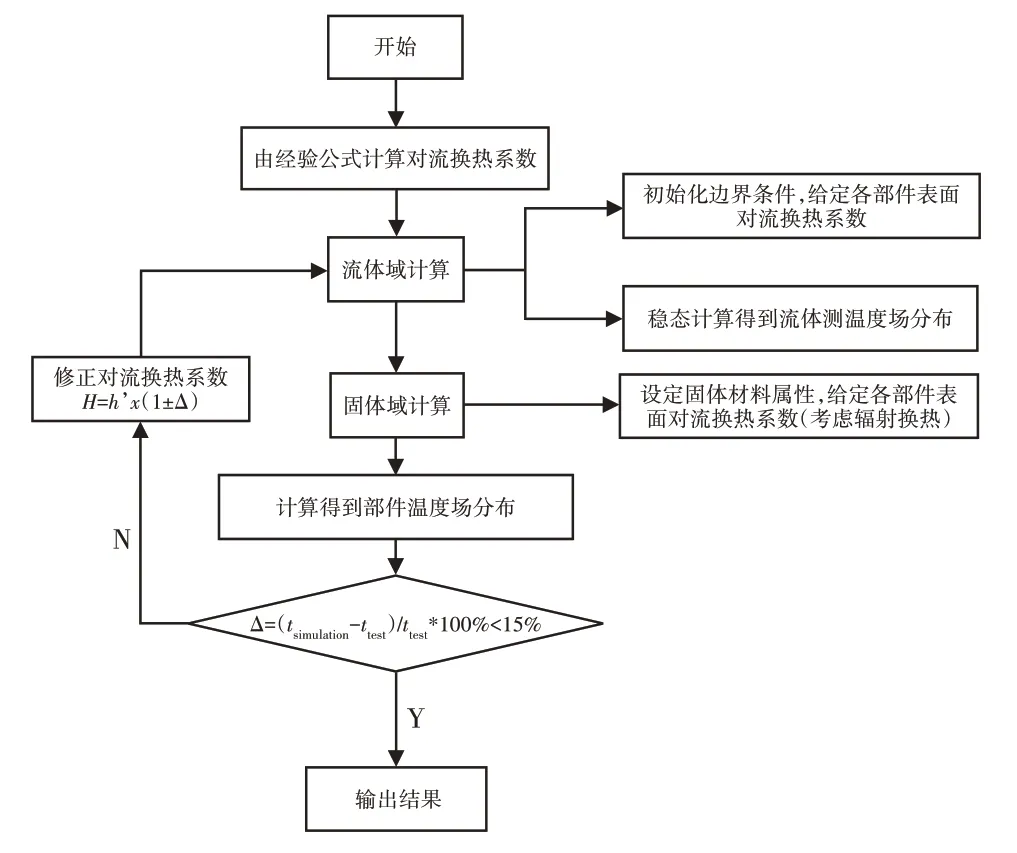
图3 耦合计算流程Fig.3 Coupled Computing Flow
3.2.2 仿真计算
计算域分为流体域和固体域,网格划分均采用多面体网格,流体域网格数量为500万左右,固体域网格数量为300多万。热浸工况下,采用层流模型;设置入口条件为停滞入口,出口条件为压力出口。其他部件表面均为壁面,环境温度为300K。考虑热辐射[7],辐射模型采用S2S。辐射角系数以及固体导热系数,如表2所示。
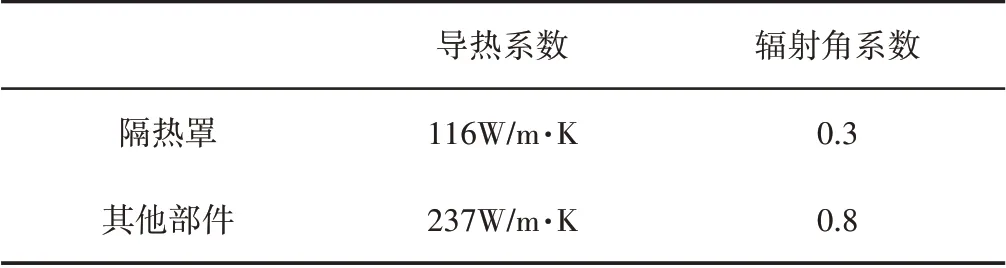
表2 机舱内各部件换热系数Tab.1 The Heat Transfer Coefficient of the Components
4 结果分析
4.1 隔热罩表面温度场分析
隔热罩表面布置10个测点,划分为10个区域,针对每个区域的换热系数利用实验数据进行修正,并对其进行数值仿真分析,结果,如表3所示。在300℃热源下,隔热罩表面温度数值仿真结果与实验结果最大误差为-12.4%(15.8℃),最小误差为3.0%(3.4℃);400℃热源工况下数值仿真结果与实验结果的最大的误差为9.7%(12.9℃),最小误差为0.6%(0.7);500℃热源下最大误差为16.9%(29.8℃),最小误差为0.5%(1.1℃)。综合对比隔热罩表面不同测点的温度值,相对误差平均值为5.1%,数值仿真结果与实验结果能够较好的吻合。
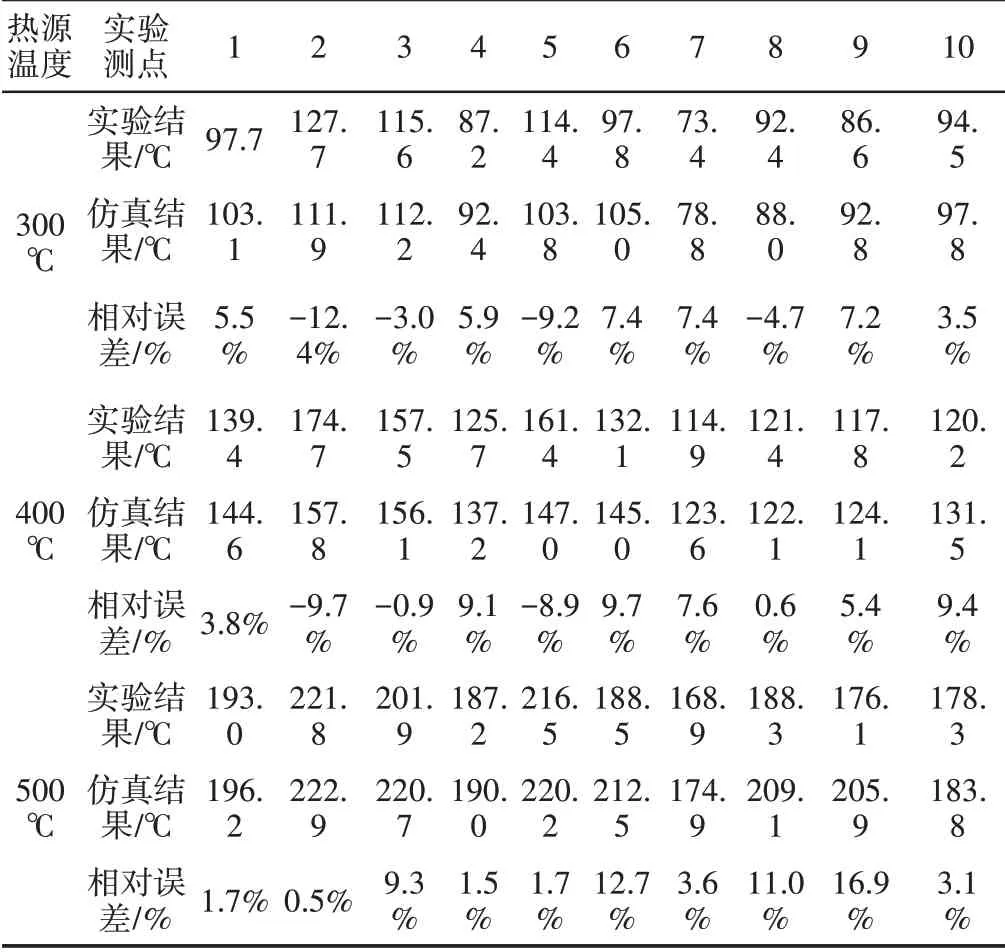
表3 隔热罩表面测点温度结果Tab.3 Heat Shield Surface Temperature Measurement Results
4.2 热浸工况下机舱内热流场温度分析
为了进一步验证仿真计算的准确性,对机舱内热流场温度分布进行分析。以上已经得出较为准确隔热罩表面的温度场分布,将隔热罩表面的温度映射到流体域,设置热边界条件为第一类热边界条件。由于热浸工况下,流体速度较低,仿真计算采用层流模型。
机舱内流场温度测点位于隔热罩前侧,即Y=1.25m截面,如图4所示。仿真结果与实验测试结果,如表4所示。可以看出,在不同热源下,热流场测点温度仿真值与实验值对比结果如下:300℃热源下平均误差仅为9.88%,且最大误差为9.68℃;400℃热源下平均误差为14.44%,最大误差为7.38℃;500℃热源下平均误差为13.63%,最大误差为9.58℃。表明仿真结果与实验测量的温度值能够较好的吻合,即可以认为采用此仿真方法的可行性。
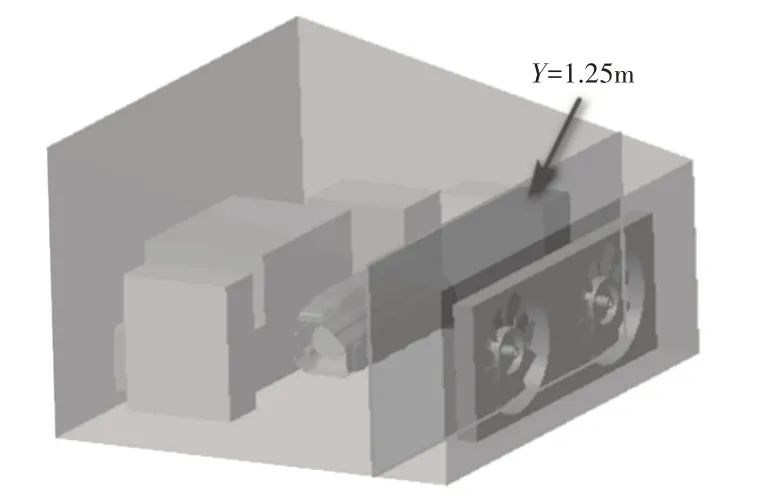
图4 Y=1.25m截面Fig.4 Y=1.25m Section
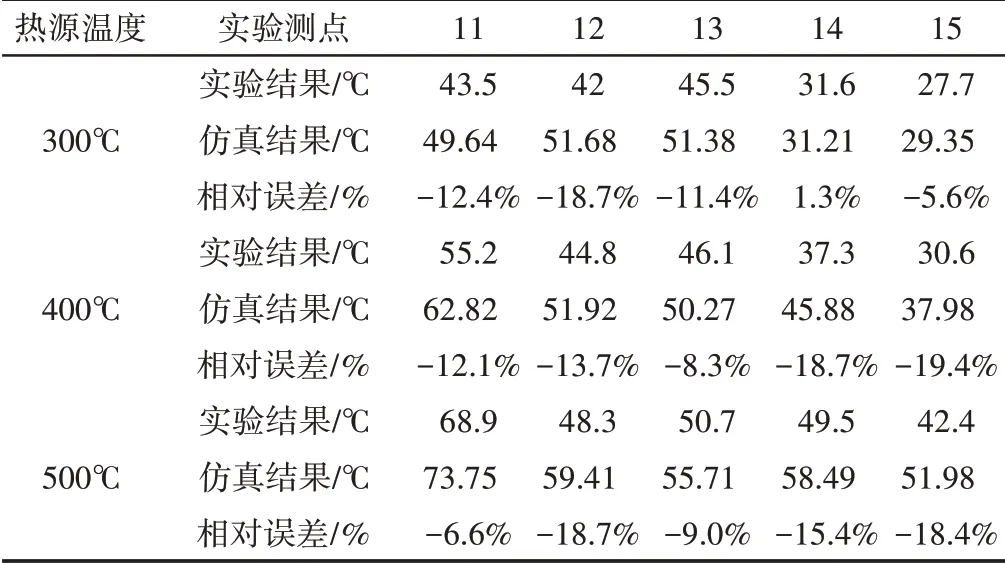
表4 流场测点温度结果(Y=1.25m截面)Tab.4 Flow Field Temperature Measurement Results(Y=1.25m)
以300℃热源为例,机舱内热流场及温度场分析,如图5、图6 所示。结果如下:热浸工况下,由理想气体状态方程可知,由于机舱内温度上升,压力升高,机舱内外存在压力差,会使机舱内的气体通过进气格栅以及出风口流出,同时由于存在重力的影响,其热空气密度小,热空气会向上流动,其流场的分布较强迫对流工况下稳定;热浸工况下流场中存在少量的涡,由图5可知,涡的存在会导致热空气在机舱内停留,不利于机舱内热量的散失。
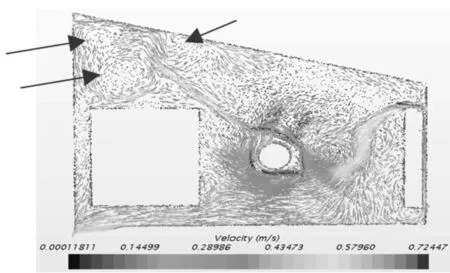
图5 热源300℃速度场截面云图Fig.5 Velocity Field Cross Section Cloud(300℃)
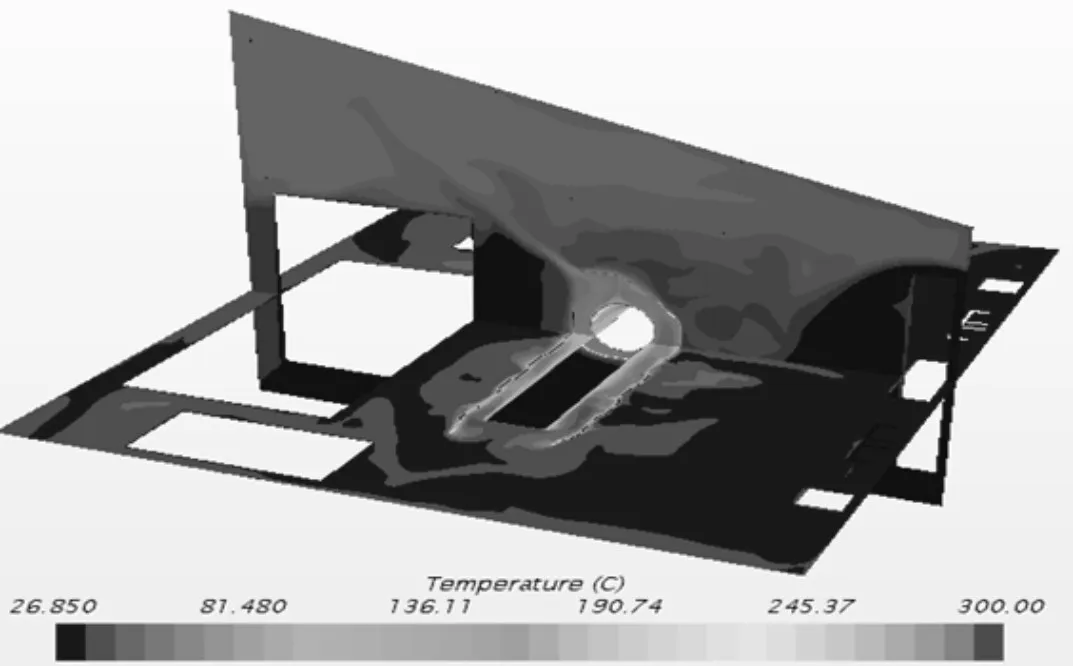
图6 热源300℃温度场截面云图Fig.6 Cross Section of Temperature Field(300℃)
4.3 对流换热系数分析
为了能够获得较为准确的机舱内温度场的分布,提出基于实验数据的修正方法,通过不断的修正对流换热系数,提高了数值仿真的效率和准确性。基于有限元的思想,对隔热罩表面测点进行分区,隔热罩表面分为10 个区域,每个区域有一个测点,根据实验测试结果对每一个区域内的对流换热系数进行修正。
由图7、图8可知,采用米海耶夫公式计算得到的对流换热系数进行数值仿真分析,三种热工况下,最大相对误差为69.5%,平均误差为30%左右;通过实验数据修正法,采用经过4次修正过后的对流换热系数仿真分析得出的隔热罩表面温度场测点误差最大为16.9%,明显降低,且平均误差仅为6%左右,有效的提高了分析结果的准确性。
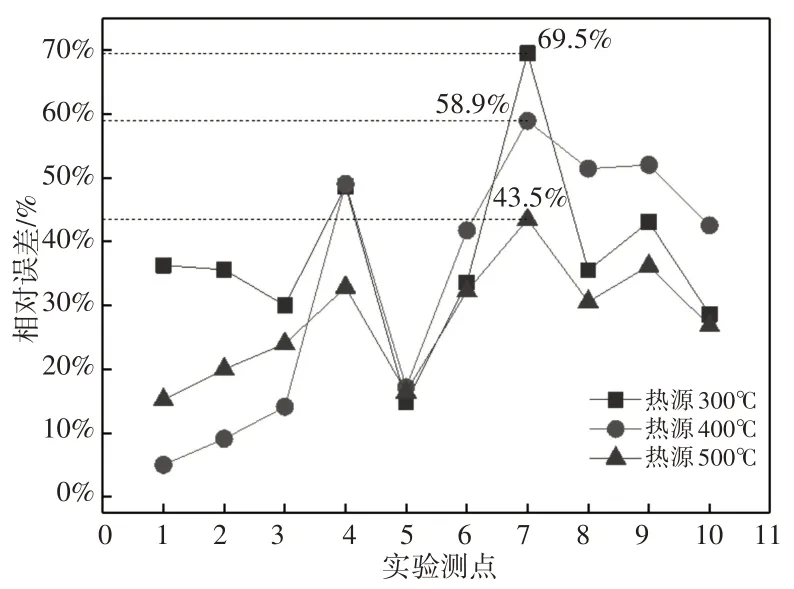
图7 初始h0a测点温度相对误差Fig.7 Initial Relative Temperature Error(h0a)
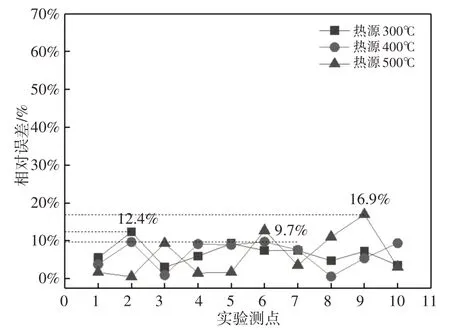
图8 修正h4a测点温度相对误差Fig.8 Correction of Temperature Relative Error(h4a)
5 结论
以发动机舱温度场为研究对象,建立简化机舱模型,搭建发动机舱温度场测试模拟台架。利用三维流体力学计算软件Starccm+,建立一种3D-3D的耦合仿真分析的方法,并通过实验测试数据验证了耦合仿真模型的可靠性,主要结论如下:
(1)通过对热浸工况下的机舱内温度场进行实验和仿真对比,采用米海耶夫相似准则关联式计算得出的温度场较实验数据误差较大;提出的基于对流换热系数实验数据修正法的思想,对比采用经验公式和基于实验数据修正法得到的结果,其经验公式有较大的局限性,而通过修正之后得到温度场结果与实验测试结果有良好的一致性,进一步验证了此方法的可行性,且此结果可对经验公式的修正有一定的参考意义;
(2)三维间接耦合仿真的方法提高数值计算的效率,且基于实验数据修正对流换热系数的方法克服了传统机舱热管理中对流换热系数的不确定性造成的困难。

