Adam优化CNN的滚动轴承多故障耦合诊断方法研究

韩 煜，张义民，张 凯，王一冰

（沈阳化工大学装备可靠性研究所，辽宁 沈阳 110142）

1 引言

滚动轴承是旋转机械的重要组成部分之一，在实际工程中滚动轴承的应用面非常广泛，轴承在运行过程中出现故障会引发很多潜在的损失和隐患，其任何意外故障往往会影响整个系统的稳定性和安全性。由于在实际工程中滚动轴承在面对不同复杂工况时，其产生的故障往往不是单一故障而是多种故障同时存在。因此针对这种多故障耦合情况，需要我们对滚动轴承进行更加准确的故障诊断。

智能故障诊断首先要从滚动轴承中采集到原始的数据，这些数据包括振动信号、脉冲信号、电流信号等诸多特征信号。振动信号是原始的时间信号，包含了滚动轴承的有用信息，无用噪声和扰动。常见的故障诊断方法有：从原始振动信号中提取和筛选有用的特征，这些特征包括峭度值、裕度值、均方根、最大值、峰值等，然后基于这些特征利用人工神经网络、支持向量机等浅层分类器进行故障分类。根据研究表明分类的结果准确度在很大程度上取决于特征的提取。目前常用的人工特征提取方法有EMD［1］、小波包分析［2］、VMD［3］、傅里叶变换等。常用的分类器模型有：DNN［5］、DBN［6］、PNN［7］等。

然而对于滚动轴承在实际工况下多种故障同时存在的问题，运用现有的特征提取后分类器训练的智能故障诊断方法还存在一些不足：特征提取方法的设计需要人工完成，这对于工作人员的专业技术和知识量要求很高；针对多种故障耦合的情况，特征提取方法很难提取到准确的特征信息；某一类特征提取方法往往只针对某一类信号适用，在实际复杂工程中效果相对较低。

深度学习最早由文献［4］作为一种新的特征学习理论提出。因此为了解决多故障耦合情况下故障诊断准确率较低的问题，这里使用Adam算法［9］和WDCNN［8］相结合的模型。该模型的两大特点：其不需要任何的人工提取特征，可以直接从原始振动信号中自主学习到分层特征信息；此外，该模型也不依赖于任何的自适应算法，也不需要任何目标域信息，同时在高扰动和强噪声情况下依然能取得良好的分类精度。经过试验验证，该方法成功解决了多故障耦合情况下故障诊断率较低的问题。用于替代深度学习神经网络的误差反向传递方法的优化算法有SGD［10］、Momentum算法［11］、RMSProp算法［12］等。

2 滚动轴承实验介绍

2.1 实验装置

本此实验所使用的实验装置为振动仪，该振动仪由交流感应电动机、电机速度控制器、支撑轴、气动轴向压力装置和气动径向压力装置等组成。振动仪，如图1所示。

图1 气动振动仪Fig.1 Pneumatic Vibrator

2.2 测试参数

该测试实验在不同工况下对滚动轴承进行振动试验。测试所用参数包括不同转速（900rpm、1400rpm、1800rpm）；轴向空载和径向空载；采样频率为40kHz；所使用轴承为6306型深沟球轴承，采集该轴承多种故障耦合和单种故障情况下的振动数据。

2.3 实验步骤

图1中1处为滚动轴承安放位置，3和4分别为轴向负载和径向负载。本次实验在空载和不同转速情况下依次对14种故障轴承和正常轴承进行测试，本次测试获取的15类故障数据，如表1所示。

表1 滚动轴承15类故障类型Tab.1 Rolling Bearing Faults of 15 Categories

表中：B—滚子表面故障；I—内圈表面故障；O—外圈表面故障；1，2，3—0.2mm，0.4mm，0.6mm的滚动轴承表面故障尺寸；N—正常。

3 卷积神经网络模型

卷积神经网络模型有两大特点：局部感受野和权值共享。这些特点减少了参数值，大大节省了训练成本，并且能够更好的挖掘原始振动数据中的特征信息。其通过卷积、池化和激活函数生成输出特征映射来分层自主学习提取特征信息，并通过全连接层和Softmax层完成最后的分类。

卷积层是卷积神经网络提取数据中特征信息的关键步骤，卷积层主要通过不同的卷积核，来获取输入信息的特征。这里我们假设和分别表示为第l层中与第i个特征映射相对应的第j个卷积核的权重和第l层中与第j个卷积核相对应的偏置，设为第l-1层中的第i个特征映射的输入。

卷积操作的公式：

式中：*—局部区域输入与卷积核进行卷积运算；—第l层中生成的第j个卷积核的输出；f(·)—一个激活函数，目前常用的激活函数有Sigmoid函数、Tanh正切函数等。

在这里我们使用了整流线性单元函数（ReLU）作为卷积神经网络的激活函数，该激活函数能够加快卷积神经网络的收敛过程，使学习到的特征具有更强的可分性。

卷积层之后都有一个池化层，称为降采样层，用于降低输入特征映射的分辨率，使卷积神经网络具有更强的鲁棒性。

公式如下：

—上一层卷积层的输出特征映射；

S—池化层的尺寸范围。

全连接层是将进过若干卷积，池化操作后的特征映射依次按行展开，连接成一维向量。然后运用Softmax函数获得15中不同滚动轴承健康状况的概率分布。

Softmax表达式：

式中：qj—卷积神经网络的分类输出结果；

zj—第j个输出神经元的对数。

本次实验运用了WDCNN［8］模型，该卷积神经网络在第一层卷积中设置一个较大的卷积核，主要是为了过滤掉大部分的噪声和扰动。然后在后面的卷积层设置几个较小的跟随卷积核。神经网络中层的深度增加，步长的减小会使神经元的数量增加，使模型的信息挖掘能力更强，性能更好，但是也可能会发生过拟合现象。因此面对大样本训练数据，我们需要更深的卷积神经网络模型和合适的参数设置去实现准确的滚动轴承故障诊断。实验采用Tensorflow 工具箱来实现，该神经网络模型，如图2所示。

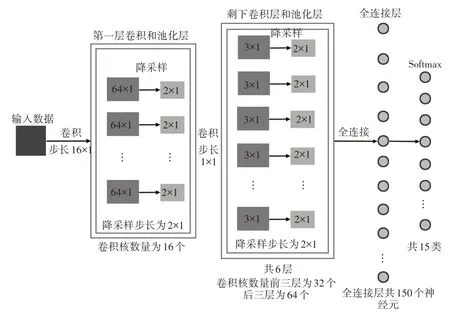
图2 WDCNN模型Fig.2 WDCNN Model

4 Adam算法

Adam［9］算法是深度学习的一种误差反馈优化算法，用Adam算法替代WDCNN模型在深度学习中传统的梯度下降方法，优化WDCNN中的交叉熵损失函数（5），由于Adam算法优化的WDCNN神经网络模型的损失函数是非稳态目标，所以在该算法中对没有设置约束条件。使深度学习的性能得到了提高。Adam算法的实现原理：对梯度的累积量和平方累积量进行初始化后，Adam算法的参数更新公式如下：

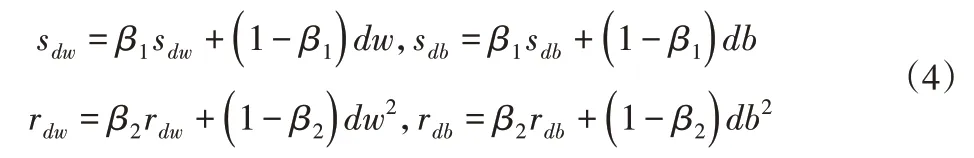
式中：sdw—一阶矩估计的权重更新量；sdb—一阶矩估计的偏置更新量；rdw—二阶矩估计的rdb权重更新量，为二阶矩估计的偏置更新量；β1，β2—超参数控制移动均值的衰减率，一般分别设为0.9和0.999。

交叉熵损失函数为：

交叉熵是两个概率分布之间的距离，式中：p—正确答案；q—预测值，交叉熵越小，两个概率的分布约接近。

在迭代开始的初期由于移动指数平均会导致与初始值有较大偏差，所以需要对更新的参数进行偏差修正：

式中：t—迭代次数—修正后的一阶矩估计权重和偏置的更新量—修正后的二阶矩估计权重和偏置的更新量。接下来通过修正后的权重和偏置结合进行更新，更新公式：

式中：α—学习率，在深度学习中初始设为0.001，然后进行微调；

ε—一个平滑项，一般取值为10-8。

5 实验验证

5.1 实验系统

为了验证使用的Adam-WDCNN 模型对滚动轴承多故障耦合诊断的效果，使用支持向量机SVM［13］、和SGD-WDCNN［8］模型这两种最常见的经典模型进行比较，参数设置与原文献相同。本次实验采用这里第2 部分的测试数据。每种工况下获得（2×40）k个数据点，使用数据类型为正负2048个数字量的数据进行测试，本次实验一组数据选取10000 个数据点，为了增加样本数，利用重叠法增加后每类故障为1000组数据，重叠法原理，如图3所示。重叠部分大小为470个数据点。15类故障共获取了15000 组数据。选择其中80% 为训练样本，10% 为验证样本，10%测试样本进行测试。

图3 重叠法Fig.3 Overlap Method

本次实验所用的卷积神经网络模型，如图2所示。该模型使用的损失函数为交叉熵函数，采用了ReLU激活函数、Softmax分类器和用Adam算法替代卷积神经网络中的随机梯度下降方法。

5.2 实验结果分析

滚动轴承原始振动数据分析结果，如图4所示。图中分别对15类故障数据截取30个数据点进行分类分析。

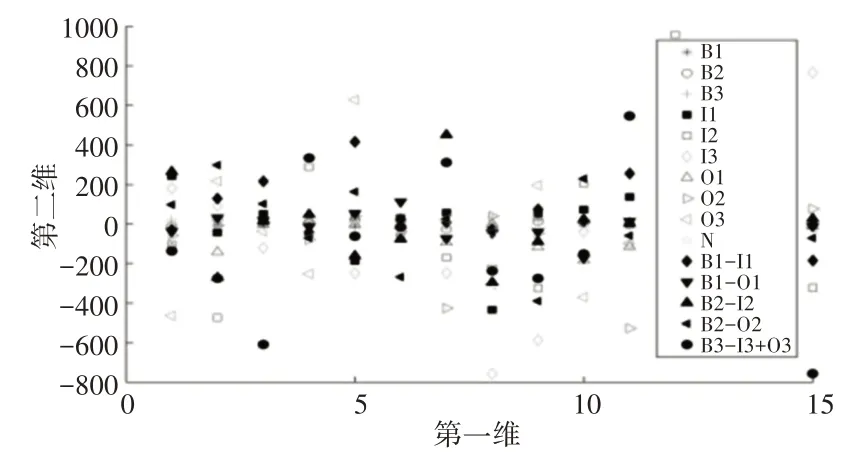
图4 故障类型分类Fig.4 Fault Type Classification

在本次比对实验中，训练过程迭代200次，神经网络模型故障诊断比较结果，如表2所示。

表2 诊断准确率对比结果Tab.2 Comparison of Diagnostic Accuracy

表2中使用的Adam-WDCNN模型运用了深度为7的卷积池化层，学习率为0.001，迭代200次，分类准确度为100%，用SGDWDCNN当学习率为0.011，准确率上升到了84.80%，支持向量机使用人工提取特征进行分类，准确度为69.534%，所以这里提出的Adam-WDCNN 模型的故障诊断效果显著优于其他故障诊断方法。

在图5中能够清楚的看到这里提出的Adam-WDCNN模型进行故障诊断时的损失函数实时变化情况。

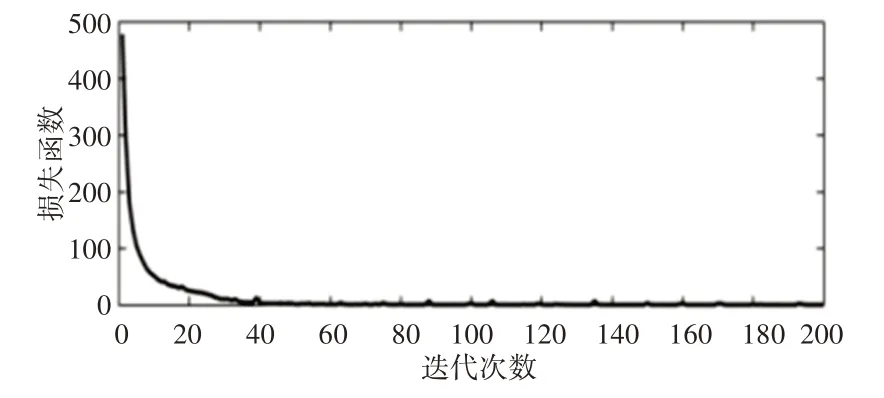
图5 损失函数收敛曲线Fig.5 Loss Function Convergence Curves

神经网络故障诊断中，损失函数的值越小意味着该模型在故障诊断中具有更高的准确率和拟合性，图4中Adam-WDCNN模型的损失函数在迭代20次左右就下降到了最优值附近，证明该模型的收敛速度比其他的一些模型更加优良，同时损失函数最终值稳定在0.041左右，非常接近于0，证明该模型准确率和拟合性非常好。

该模型利用了Dropout 方法，设置Dropout=0.5，在训练神经网络时验证集随机关闭50%的神经元，解决了神经网络训练过拟合的问题，所以当验证集的测试准确率为50%时，就相当于100%准确率。能够看到Adam-WDCNN 模型的验证集分类准确率的迭代过程，如图6所示。

图6 验证集精度Fig.6 Verification Set Accuracy

从图5中我们能够看出该模型验证集的准确率从迭代25次开始在0.413左右浮动，最终值在（0.45～0.5）之间浮动，证明Adam-WDCNN模型的验证集分类准确率很高，该神经网络模型的训练效果良好。

6 结论

（1）在处理多故障耦合轴承故障诊断问题时，实验证明Adam-WDCNN模型对于复杂情况下振动信号特征的提取效果要优于人工特征提取方法。

（2）Adam-WDCNN模型方法诊断准确率达到100%，而用随机梯度下降法替代卷积神经网络的误差反向传递过程的SGDWDCNN 模型诊断准确率为84.80%，SVM 方法的诊断准确率为69.534%。试验结果证明这里采用的Adam-WDCNN模型对多故障耦合情况故障诊断效果最优。