基于探索群策略鸽群优化的高超声速飞行器飞/发一体化控制

向宏程，邓亦敏，段海滨

（北京航空航天大学 自动化科学与电气工程学院，北京 10008）

高超声速飞行器是指速度比声速大5 倍以上的飞行器，具有飞行速度快、作战射程远、突防能力强、攻击范围广和打击效能好等优点，在军事和民用方面都有一定的应用价值[1]。2004 年，美国国家航空航天局研制的X-43A 试飞成功，标志着吸气式高超声速飞行器从实验室过渡到工程阶段[2]。

近些年来，随着世界各国的高超声速飞行器的相关技术不断发展[3-4]，越来越多的研究开始指向高超声速发动机系统和高超声速飞/发一体化控制系统[5-7]。文献[8]通过研究冲压发动机在高超飞行器工作剖面，对冲压发动机的压气系统配置进行了分析；文献[9]提出了一种高超声速飞行器发动机的供电和冷却系统，飞/发一体化的工程进展提供了一种新颖的方案；在飞/发一体化控制系统方面，文献[10]提出了具有不同发动机安全边界的高超声速飞行器飞/发一体化模型，并通过与通用高超声速飞行器的比较，验证了其模型的有效性和实用性。

然而，除了高超声速飞行器本体具有飞行环境复杂、空间环境变化剧烈、内部参数及结构不确定性强等特点[11]外，气流一体化、结构一体化等耦合作用也使得高超声速飞行器飞/发一体化控制系统设计具有一定挑战[12]。因此，提出一种满足强耦合控制系统的参数整定方法具有相当重要的研究价值。

受自然界中鸽子归巢行为启发的鸽群优化算法（pigeon-inspired optimization,PIO）在控制参数优化方面具有较高收敛速度[13]。自Duan 等[14]提出以来，鸽群优化算法及其改进模型已广泛应用于众多领域[15-17]。文献[15]提出了拟仿射变换鸽群优化算法，这种改进的鸽群机制为无线传感器网络提供了一种有效的解决方案。文献[16]提出了一种紧密鸽群优化算法，并应用于评估水电站短期发电模型的最大值。在针对狭窄区域内多无人机路径规划性能的研究方面，文献[17]提出了一种柯西变异鸽群算法，比传统方法具有更好的鲁棒性。

针对高超声速飞行器飞/发一体化控制问题，本文首先建立了高超飞行器飞/发一体化系统模型，并针对该系统设计了纵向控制律。针对高超飞行器飞/发一体化控制系统难以调试的问题，本文基于基本鸽群优化算法，提出了一种新型的探索群策略鸽群优化算法，该算法基于探索群的辅助搜索，可有效解决基本鸽群优化算法容易很快陷入局部最优的问题。最后，针对所设计的飞/发一体化控制系统，通过探索群鸽群优化算法对其控制参数进行优化，并与基础PIO 算法、粒子群优化算法(particle swarm optimization,PSO)进行了仿真对比验证，实验结果验证了本文所提探索群鸽群优化算法在解决飞/发一体化控制参数整定问题方面的可行性和优越性。

1 高超飞行器飞/发一体化系统模型

本文在对高超飞行器本体进行建模时[18]，将飞行器视为刚体，忽略弹性耦合及质量变化。其纵向运动学及动力学方程为

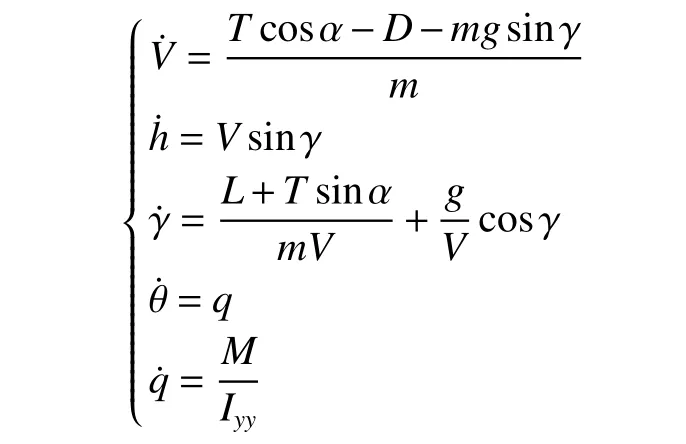
式中：[T,L,D,M]为飞行器的动力输入，分别为飞行器推力、升力、阻力、俯仰力矩；[V,h,γ,θ,q]为飞行器的状态量，分别为飞行速度、飞行高度、航迹角、俯仰角、俯仰角速度；α为飞行迎角，以式α=θ −γ 计算；[m,Iyy]为飞行器的惯性参数，分别为飞行器质量和转动惯量。

升力、阻力、俯仰力矩的计算公式为

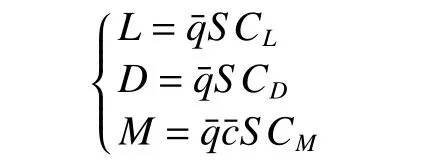
式中：为动压，以式计 算；[S,]为飞行 器几何参数，分别为参考机翼面积、平均气动弦长；[CL,CD,CM]为飞行器气动导数，计算公式为

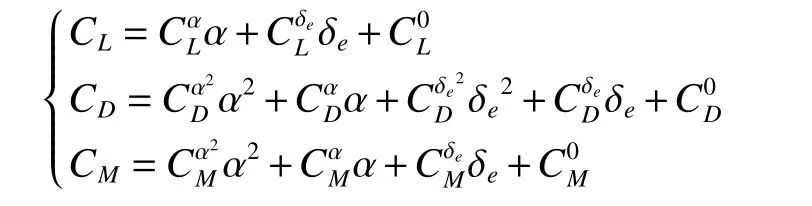
式中 δe为飞行器控制量，表示升降舵偏角。

飞行器惯性参数、几何参数、气动参数见文献[18]。飞行器推力由发动机模型提供，认为发动机本身的动态响应可以忽略，在发动机的计算中不考虑时间项，将发动机模型按照稳态计算。

一维简化冲压发动机模型由进气道、燃烧室、尾喷管3 个部分组成[19]。进气道、燃烧室、尾喷管特性的计算公式分别如式(1)～(3)所示。

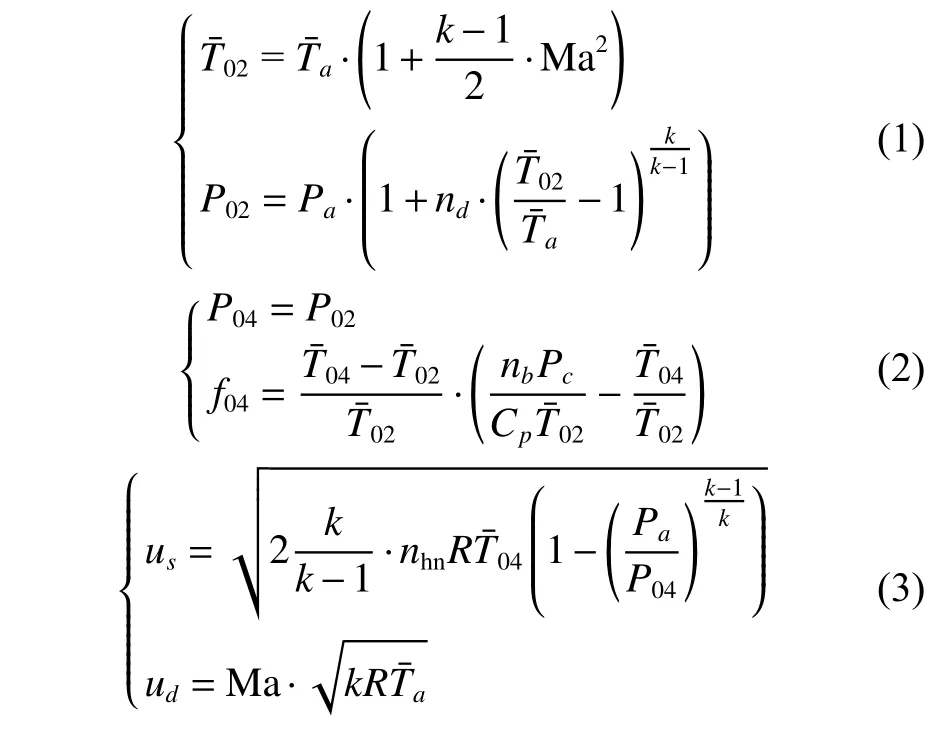
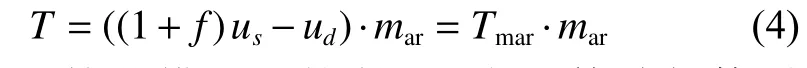
式中：mar为简化模型的控制量，表示等效气体质量流量。

2 飞/发一体化系统纵向控制律设计

本文重点研究高超飞行器爬升过程中的飞/发一体化高度控制，即自主爬升、降落过程中，保持飞行速度基本稳定，通过升降舵及发动机协调工作，对航迹角进行控制从而达到高度控制的目的。首先设计高超飞行器纵向多回路高度控制，由高度指令href经控制律求解出升降舵 δe偏角变化量 Δδe，由内至外为俯仰角速度q、俯仰角θ、高度h的控制回路。俯仰角速度控制回路目标为俯仰角速度指令qdes的跟踪控制，其控制律计算公式为

俯仰角速度控制回路的输入指令由俯仰角控制回路得到，其目标为俯仰角指令 θdes的跟踪控制，其控制律计算公式为

俯仰角控制回路的输入指令由高度控制回路得到，其控制目标为高度输入hre f的跟踪控制，其控制律计算公式为

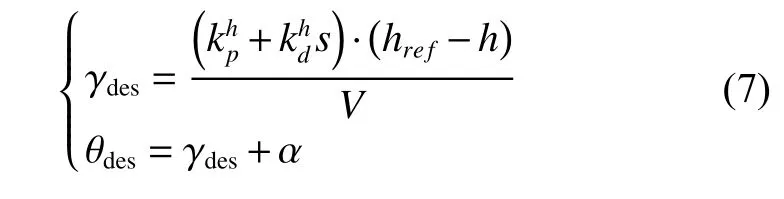
由式(5)～(7)可实现高超飞行器升降舵对高度输入的响应，为实现高度爬升过程中的速度稳定，还需设计推力通道的速度及迎角稳定控制回路，以求解稳定推力Ts基础上的推力变化量 ΔT，由速度及迎角控制分别得到其分量 ΔTV及ΔTα。

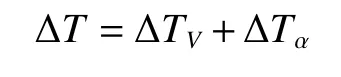
速度控制目标为由初始稳定速度Vs的稳定控制求解出推力变化量 ΔTV，其控制律计算公式为

迎角控制目标为在具有较大高度爬升需求时稳定住迎角以获得较大纵向航迹倾斜角，从而获得较大爬升速率。由于迎角控制与速度稳定为互斥过程，因此在高度爬升需求较小时需要去掉对迎角的控制以保证速度的稳定。由初始稳定迎角αs的输入求解出推力变化量 ΔTα控制律的计算公式为

由式(1)～(4)可知：

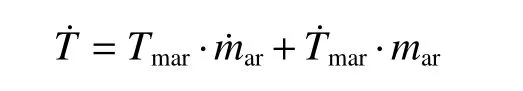
式中：Tmar随飞行高度和马赫数变化，可视为慢变量，本文忽略其变化率，从而推导出推力控制律公式为

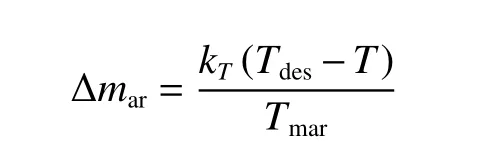
高超飞行器飞/发一体化系统整体控制结构如图1 所示。

图1 飞/发一体化控制系统结构Fig.1 Diagram of flight engine integrated control system

3 探索群策略鸽群优化算法

3.1 基本鸽群优化算法

基本鸽群优化算法受启发于鸽群归巢机制[14]，根据鸽群归巢的不同阶段的行为特点，PIO 算法由两部分组成，分别为地图和指南针算子，以及地标算子。

在PIO 算法中，假定鸽群数量为N,每只鸽子有D维位置坐标Xi=[xi1,xi2,···,xiD] 及速度坐标Vi=[vi1,vi2,···,viD]。

1) 地图与指南针算子

鸽群归巢行为的第一阶段，鸽群凭借太阳高度及方向判断方位，作为PIO 算法的地图与指南针算子，其更新公式为

式中：R为地图因子，Xgbest为全局最优位置。

2) 地标算子

鸽群归巢行为的第二阶段，鸽群凭借地标进行导航，作为PIO 算法的地标算子，其更新策略为

式中：NN(t) 为t时刻的鸽群个体数 目；Xcenter(t)为t时刻鸽群中 心位置；fitness(Xi) 为第i只鸽子的适应度值。

3.2 探索群策略鸽群优化算法

为提高基本鸽群优化算法在复杂控制系统参数优化过程中的全局搜索能力，本文提出了探索群策略鸽群优化算法(exploring swarm pigeon-inspired optimization,ESPIO)，具体介绍如下。

初始化阶段，将基本鸽群划分为两个子群，分别记为主群与探索群。搜索阶段，主群负责进行常规搜索，其搜索方式与基本鸽群一致；探索群负责对新区域进行探索，其搜索方式为

式中：Re为探索群的地图因子，其值受前一轮迭代的结果影响；Xm为每轮迭代中最优的两只鸽子的平均位置。Re更新方式为

式中：Rmin、Rmax分别为地图因子设定的最小值、最大值，本文中分别取0.01、0.03；pi表示第i只鸽子的适应值，pmax为 适应值的最大值；定义 ζ为迭代进度指数，当全局最优有更新时将其值设置为1，此时Re小 于主群地图因子R，探索群鸽子更偏向于保持当前搜索速度值；反之，全局最优没有更新时，将 ζ设置为0，此时Re大于主群地图因子R，探索群鸽子更偏向于更新当前搜索速度值；此外，无论ζ为何值，适应值越小的鸽子其位置越优，Re越小，更趋近于保持原本速度。

Xm计算方式为

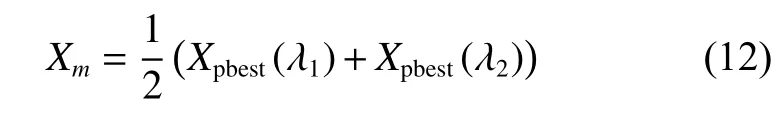
式中：以 λ1和 λ2分别记录适应度最优的两只鸽子，则Xpbest(λ1)和Xpbest(λ2)分别表示适应度最优的两只鸽子的历史最优位置，因此保证Xm是接近问题的优化方向的；同时由于两只鸽子可能出现在不同的局部最优点，因此其平均值具有一定随机性，体现出一定的探索能力，可降低主群陷入局部最优的概率。

3.3 飞/发一体化系统优化策略

高超飞行器速度、高度跨越较大，以常规的时间加权积分绝对误差(integral time-weighted absolute error，ITAE)准则作为控制系统参数优化的适应度函数时[20]，由于高度指令href跳转时与初始值的偏差过大，导致其掩盖动态过程中及稳态时的性能。因此在ITAE 的基础上，将时间加权改为时间的平方项，更能侧重控制的稳态性能，即

本文所提ESPIO 算法，以基本鸽群算法为基础，为解决其容易陷入局部最优的问题，设置探索群为主群提供额外搜索信息。以探索群策略鸽群优化算法进行飞/发一体化控制参数整定的具体实现流程如图2 所示。

图2 探索群策略鸽群优化算法流程Fig.2 Flow of exploring swarm pigeon-inspired optimization

算法具体步骤为：

1)选择飞/发一体化系统配平状态，包括飞行器平衡状态及对应发动机的控制量mar；

3)随机分配1/4 鸽子为盘旋群；

4)运行飞/发一体化控制仿真系统，并计算该组控制参数适应值；

5)对于主群的鸽子，以式(8)更新其速度与位置；对于盘旋群鸽子，首先以式(11)更新探索群地图因子，再以式(12)计算两只最优鸽子的平均位置，最后以式(10)更新速度与位置；

6)满足地图及指南针算子迭代次数后，以式(9)更新鸽子数量及位置。否则，返回4)；

7)满足地标算子迭代次数后，输出优化结果。

4 飞/发一体化优化控制仿真及分析

采用MATLAB/Simulink 作为仿真软件，搭建高超飞行器飞/发一体化模型及控制系统，将ESPIO 算法用于控制系统参数优化，并与基本PIO 算法、PSO 算法的优化结果进行对比。优化参数包括推力控?制系数kT，高度控制回路参数迎角控制回路参数速度控制回路参数

3 种智优化算法的迭代曲线如图3 所示，最终适应度函数值如表1 所示，由探索群鸽群优化算法优化后的变量如表2 所示。

表2 优化后变量Table 2 Optimized parameters

图3 参数优化迭代曲线Fig.3 Parameter optimization iteration curve

由图表可得，对于高超飞行器飞/发一体化控制系统，其各个控制通道、各个控制回路之间耦合较强，在参数整定时极易陷入局部最优，本文所提出的ESPIO 算法在全局最优的探索方面表现突出，最终得到的适应值最好。

以优化结果作为控制参数，在20 000 m 初始高度、885 m/s 的初始速度（马赫数3）的平飞状态下进行高超飞行器的高度控制仿真，给定2 000 m高度阶跃指令，高超飞行器高度跟踪曲线如图4所示，速度保持曲线如图5 所示。

由图4 可知，在高超飞行器高度控制的仿真结果中，3 种算法得到的结果均无超调量；以ESPIO 算法参数得到的结果调节时间最短，而以PSO 算法参数得到的结果调节时间最长。由图5 可知，在高度控制的同时进行速度保持控制，3 种算法得到的结果均能使速度误差不超过0.045%，其中ESPIO 算法参数得到的误差最小，其值为0.037%。而在34 s 处，ESPIO 得到的结果具有最高的误差，因为此时对应的高度控制具有最快的收敛速度，由于高超飞行器飞/发一体化系统各个通道的强耦合特性，其速度波动会更剧烈，但速度波动的最大值不超过当前稳定速度的0.01%。因此，以ESPIO 优化得到的控制参数，在高超飞行器飞/发一体化控制器参数整定方面有最好的优化效果。

图4 高度控制曲线Fig.4 Altitude control curve

图5 速度控制曲线Fig.5 Velocity control curve

5 结束语

1）本文针对高超飞行器飞/发一体化系统设计了纵向控制器，包括升降舵通道的各个回路及推力通道的速度回路及迎角回路，另外还包括发动机的推力控制。最后对高度跟踪控制进行了仿真，其结果表明所设计的控制器能够满足一定的控制精度与稳定性。

2）本文所提出的ESPIO 算法与基本PIO、PSO 相比具有更好的收敛性，通过对高超飞行器飞/发一体化控制器参数整定并进行控制仿真，得到仿真结果对比，其结果表明，本文所提出ESPIO 算法在高超飞行器飞/发一体化控制器参数整定方面有最好的优化效果，即在保持速度基本稳定的同时，具有最好的高度控制性能。