基于随机响应面法的斜坡基桩水平承载可靠性分析

尹平保，王杰，张建仁，王康

（1.长沙理工大学土木工程学院，湖南长沙 410114；2.桥梁工程安全控制教育部重点实验室（长沙理工大学），湖南长沙 410114）

为守护“绿水青山”、实现“碳中和、碳达峰”，在我国西部山区修建高速公路和铁路时，主要采用高架桥的方式跨越江河、峡谷或空洞等特殊地区.为此，不可避免地将桥梁基桩设置在高陡斜坡上.现有研究表明，对位于斜坡上的桥梁基桩，其水平承载特性与常规的平地基桩差异显著［1］，为确保斜坡段桥梁基桩的安全与稳定，很有必要对其水平承载机理及可靠性展开深入系统的研究.

有关斜坡基桩水平承载特性，已有部分学者对其展开了一些有益的研究，如：赵明华等［2-3］根据高陡斜坡上桥梁基桩的受力特点，通过基桩水平承载极限分析，研究了斜坡坡度、地基抗力折减系数对桩身水平位移及承载力的影响；Zhuang 等［4］基于抗剪强度折减法，分析了斜坡坡度对基桩安全系数的影响；Sivapriya 等［5］通过室内模型试验与有限元分析，研究了斜坡坡度对基桩水平承载力的影响.上述研究均表明，斜坡坡度的存在对基桩水平承载特性的影响非常显著，很有必要对其展开深入研究.实际上，桩、土参数的不确定性对基桩水平承载性能的影响也不容忽视，因此，基于水平变形和材料屈服等失效模式，开展基桩水平承载可靠性研究非常重要.Chan 等［6］结合响应面法与神经网络法，分析了桩、土参数的相关性对基桩水平承载可靠性的影响；Kozubal 等［7］将气候作为随机变量，采用响应面法与多项式回归相结合的方法，开展了复杂环境下基桩水平承载可靠性分析；赵明华等［8］克服极限状态方程无法收敛等难题，提出了改进响应面法，并将其用于倾斜荷载桩的可靠性分析；Chan和Low［9］基于挠度和弯矩两种破坏模式，分析了桩长和桩径对水平受荷桩可靠性的影响.综上所述，目前有关基桩水平承载可靠性的研究多针对平地桩，而对斜坡基桩的分析显然不够.因此，为确保斜坡基桩的安全与稳定，进一步考虑斜坡坡度的影响，对其水平承载可靠性开展深入研究显得尤其重要.

鉴于此，本文在现有研究基础上，首先分析斜坡效应对基桩水平承载特性的影响，建立基桩简化受力模型及挠曲微分方程，导得相应的理论解答；其次，基于随机响应面法，建立斜坡基桩水平承载可靠性分析极限状态函数，并通过编程求解可靠度指标；最后，结合已有算例，对比分析理论方法及程序的合理性，进而探讨参数不确定性和斜坡效应对基桩水平承载可靠性的影响.

1 考虑斜坡效应的基桩受力分析

1.1 简化受力模型及挠曲微分方程

对位于斜坡上的桥梁基桩，为研究斜坡坡度对其受力特性的影响，可沿桩身轴心方向将基桩划分为斜坡影响段（l1）和嵌固段（l2）.在桩顶水平荷载H和偏心弯矩M的共同作用下，可建立如图1 所示的简化受力模型［10］.

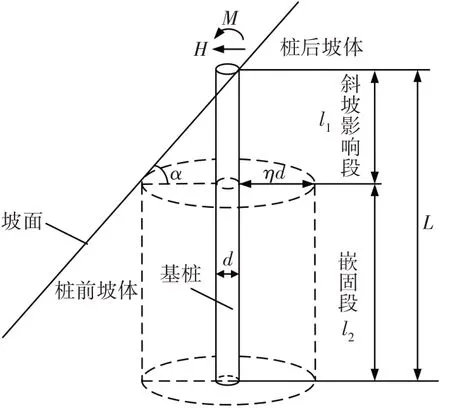
图1 斜坡基桩简化受力模型Fig.1 The simplify model of piles in sloping ground

图1 中，因存在斜坡坡度，桩前l1深度范围内出现一临空面，使得基桩两侧岩土体不对称，桩前坡体一定深度范围内的岩土体水平抗力有所减弱，此即所谓的“斜坡效应”［11］.其中，l1为斜坡效应影响深度，其计算表达式为：

式中：η为斜坡效应折减系数，现有研究表明［10］斜坡效应影响范围为3～5 倍桩径，即η可取3～5；d为桩径；α为坡度.

根据图1 所示的简化受力模型，通过受力分析，可建立考虑斜坡效应的基桩挠曲微分方程：

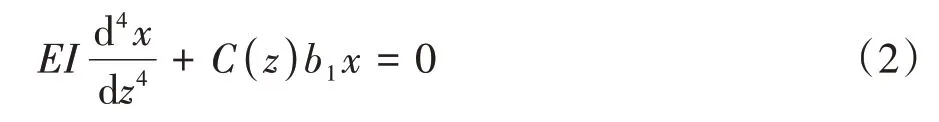
式中：EI为桩身抗弯刚度；x为桩身水平位移；z为计算点到桩顶的距离；C（z）为桩侧地基抗力系数；b1为桩身计算宽度.

根据m法，并综合考虑斜坡效应的影响，假定桩侧地基抗力系数C（z）表达式为［10］：

式中：m为地基抗力比例系数，其他参数同前.

1.2 基桩受力分析的有限差分法

为求解基桩挠曲微分方程式（2），根据中心差分原理，可将基桩斜坡影响段（l1）和嵌固段（l2）共划分为段长均为h的N段，并在桩顶和桩端分别增加两个虚拟节点，即共生成（N+5）个节点，各段间的差分节点布置如图2所示.

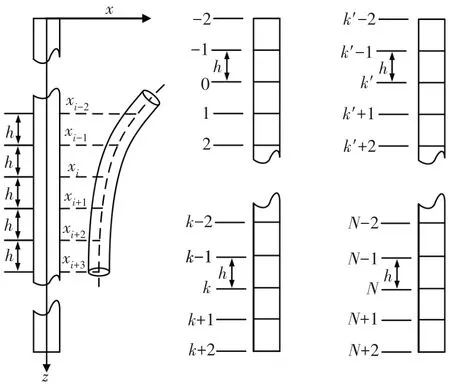
图2 基桩差分点布置Fig.2 Differential point arrangement of the pile

实际工程中基桩边界条件可分为自由、弹嵌、嵌固和铰支4 种情况［12］.本文假定桩顶自由、桩端嵌固，其对应的边界条件差分格式为：

1）桩顶自由

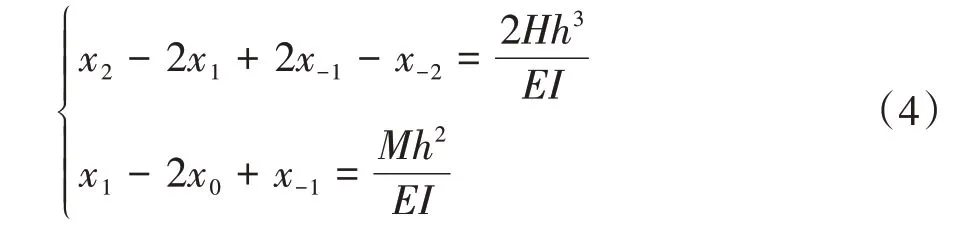
2）桩端嵌固

对于基桩斜坡影响段（0＜z＜l1），节点i（i＜K=l1/h）处的控制差分方程为：

基桩桩身转角、弯矩和剪力的差分格式为：

式中：xi为节点i处的水平位移；φi为节点i处的转角；Mi为节点i处的弯矩；Hi为节点i处的剪力.

由式（6）可得桩顶（i=0）处的控制差分方程为：

将式（4）代入式（8）可得：

联合式（4）和式（6），并令i=1，2，3，…，K，可得基桩斜坡影响段（0＜z＜l1）各节点的位移递推式：

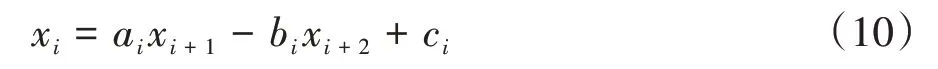
根据i=0 和i=-1 时对应的a-1，a0；b-1，b0；c-1，c0等值可得各节点参数的表达式为：

对于嵌固段（l1＜z＜L），节点i（K≤i＜N=L/h）处的控制差分方程为：

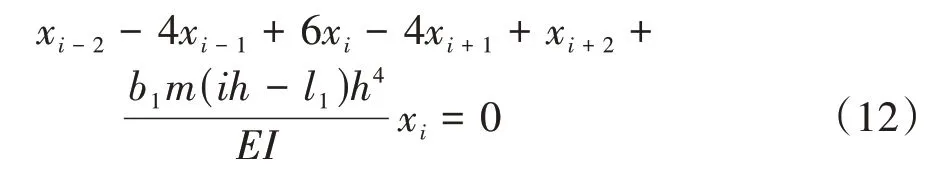
联合式（5）和式（12），并令i=K，K+1，K+2，…，N，可得嵌固段（l1＜z＜L）各节点的位移递推式：

根据i=N-1 和i=N-2 时对应的aN-1，aN-2；bN-1，bN-2等值，可得K≤i≤N-3时的参数表达式为：

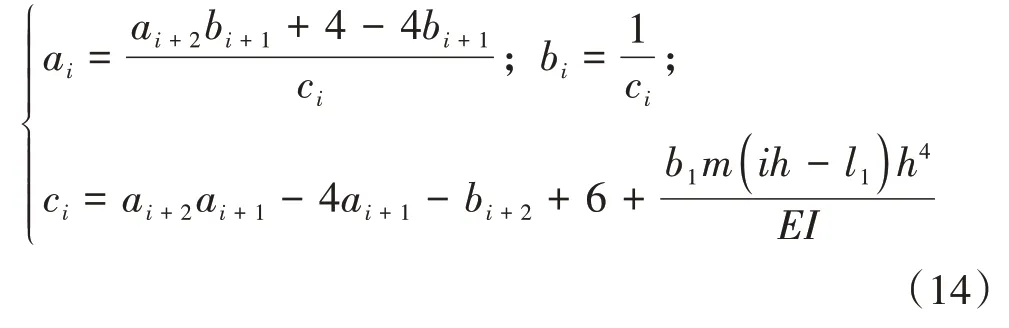
由节点位移递推式（10）（13）以及节点参数表达式（11）（14），即可求得交界点K及其邻近节点的位移；然后，通过节点位移递推式（10）（13）求得各节点位移；进而将各节点位移代入式（7）即可求得各节点的转角、弯矩和剪力［13］.

2 斜坡基桩可靠性分析

构件截面抗力的随机性主要体现在材料性能、几何参数和计算模式等方面.现有研究表明，水平受荷桩的失效模式主要有桩顶水平位移过大和桩身材料屈服（桩身内力超过材料屈服强度）［8］.通常情况下，对于变异性较小的参数，可将其作为确定性参数，而将变异性较大的参数当作随机变量.假设随机变量为y1，y2，y3，y4，…，yn，则对应的随机向量Y=（y1，y2，y3，y4，…，yn）.因此，相应失效模式下基桩极限状态函数可表示为：

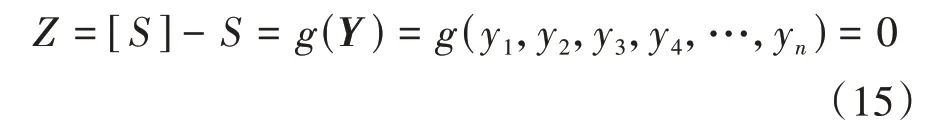
式中：［S］为相应失效模式下参数容许值；S为计算得到的最大值；Z为安全余量.

2.1 极限状态函数的建立

关于基桩可靠性分析，目前主要有蒙特卡罗法（MCS）、一次二阶矩法（JC）以及响应面法（RSM）等［14-15］.对于高阶非线性函数或隐式函数，蒙特卡罗法的计算量较大，实用性不强；一次二阶矩法无法求解隐式函数；响应面法和改进响应面法均是利用显式响应面函数拟合较复杂的极限状态函数，两者虽可求解可靠度指标，但收敛性很难保证，且二者对高阶非线性极限状态函数的计算精度并不高［15］.为解决以上问题，可采用随机响应面法（SRSM）拟合出相应的极限状态函数.随机响应面法是通过展开的Hermite 随机多项式来拟合随机变量之间的函数关系，再根据隐式的极限状态函数，利用一次二阶矩法（JC 法）求解可靠度指标及失效概率［16-19］，具体过程如下.

1）首先根据需要展开的Hermite 随机多项式阶数p和随机变量个数n确定待定系数个数Na、配点值W和选择的配点总数Nb，其计算表达式为：

式中：Nb＞＞Na，可采用线性无关原则选取所需的配点.配点值W为p+1阶一维Hermite多项式的根.

2）将随机变量yi转换成服从标准正态分布的随机变量Xi，其转换关系为：

3）利用Hermite 随机多项式将极限状态函数（15）展开，可得安全余量Z为：

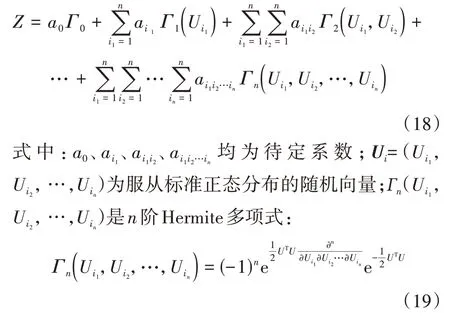
4）将步骤1）中选取的配点值W与步骤3）中的安全余量Z分别代入式（18），求解等待定系数，即可得到显式的极限状态函数.

2.2 可靠性分析

根据得到的极限状态函数，采用一次二阶矩法（JC 法）求解基桩水平承载可靠度指标及失效概率.具体求解过程为：

1）假定初始验算点Y*，一般可取Y*=μY.

3）确定新的设计验算点Y*：

4）重复步骤2）至4），直至前后两次||Y*||之差＜允许误差ε，ε通常为0.001.

5）根据可靠度指标β计算失效概率：

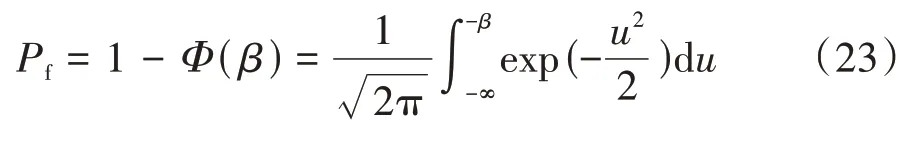
式中：Φ（·）为服从标准正态分布的累计分布函数.

3 工程实例及可靠性分析

3.1 工程概况

湖南省张（家界）花（垣）高速公路泗溪河一桥采用桩柱式基础，基桩设置在坡度为30°～60°的斜坡上.该基桩采用C25混凝土，桩长为25 m；桩径d均值为2 m，标准差为0.04 m；桩身弹性模量E均值为28 GPa，标准差为0.56 GPa.各土层地基抗力比例系数m均值为60 MN/m4，标准差为12 MN/m4.基桩纵筋为46ϕ25 的HRB335 钢筋，通长配置.桩顶弯矩M为1 200 kN·m；水平荷载H均值为150 kN，标准差为30 kN；桩顶容许水平位移为6 mm；桩身抗弯承载力为4 561 kN·m.

3.2 基桩水平承载可靠性分析

1）取等量差分段长h=0.05 m，斜坡效应折减系数η=5，坡度为45°，则斜坡效应影响深度l1=10 m.

2）将桩身弹性模量E、桩径d、桩顶水平荷载H、地基抗力比例系数m值作为随机变量，并假定各随机变量均服从正态分布，且相互独立［8］，则随机变量的个数n=4、其对应的随机向量为：

3）根据式（17）（18）及（24），即可建立随机变量的个数n=4、最高阶数为3 的Hermite 随机多项式，即将其按最高阶数展开得到基桩水平承载失效模式下的随机响应面函数为：

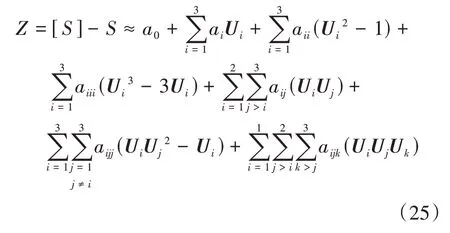
式中：a0、ai、aii、aiii、aij、aijj、aijk为35 个待定系数；Ui、Uj、Uk均为服从标准正态分布的随机向量（i、j、k按式（25）进行取值）.

4）采用概率配点法选取4 阶一维Hermite 多项式，并将其根作为配点进行正态分布转换，经计算得到256个安全余量Z.

5）选取35 组配点及对应的安全余量Z可解35个待定系数，并将其代入式（25）.

6）根据式（25）求解桩顶水平位移和材料屈服失效模式下的可靠度指标β和失效概率Pf.

利用蒙特卡罗法（MCS）模拟1×106次、改进响应面法（RSM）和随机响应面法（SRSM）计算得到的可靠度指标及失效概率如表1所示.

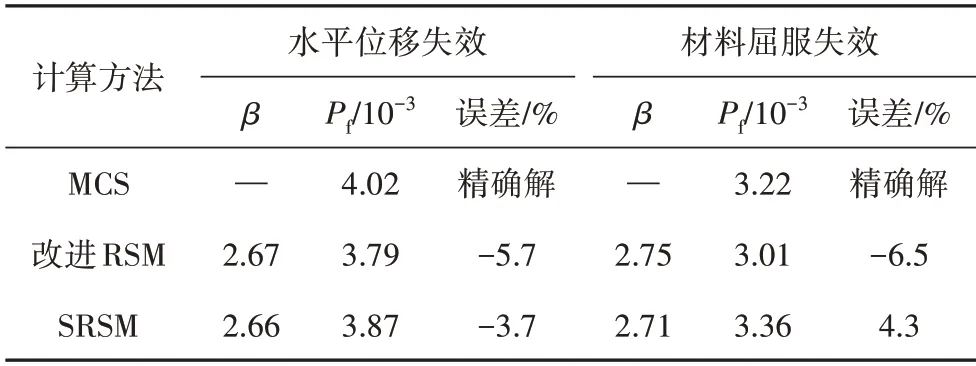
表1 计算结果对比Tab.1 Comparisons of calculation results

由表1 可以看出，以MCS 作为精确解，由改进RSM 计算得到的失效概率明显偏小.相对而言，SRSM 的计算结果与MCS 更接近，从而可以验证SRSM方法及计算程序的合理性.

3.3 参数不确定性分析

以上述工程为例，进一步分析了地基抗力比例系数m、水平荷载H、桩身弹性模量E以及桩径d等参数的不确定性对基桩可靠性的影响.相应失效模式下，各参数变异系数与基桩失效概率的关系曲线如图3和图4所示.

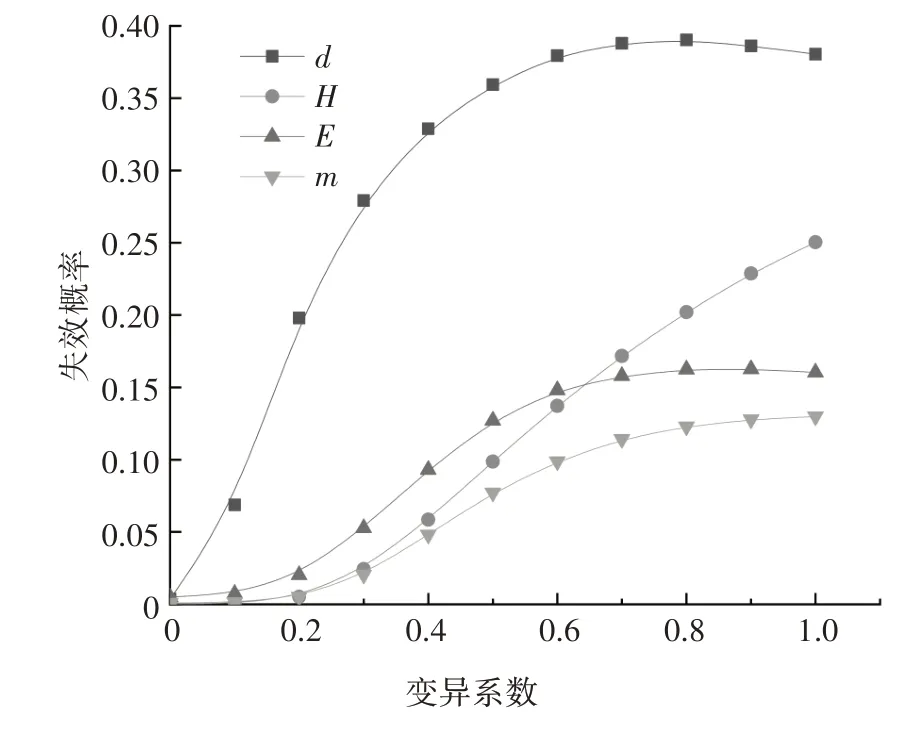
图3 水平位移失效下变异系数对失效概率的影响Fig.3 Influence of variation coefficient on failure probability under horizontal displacement failure

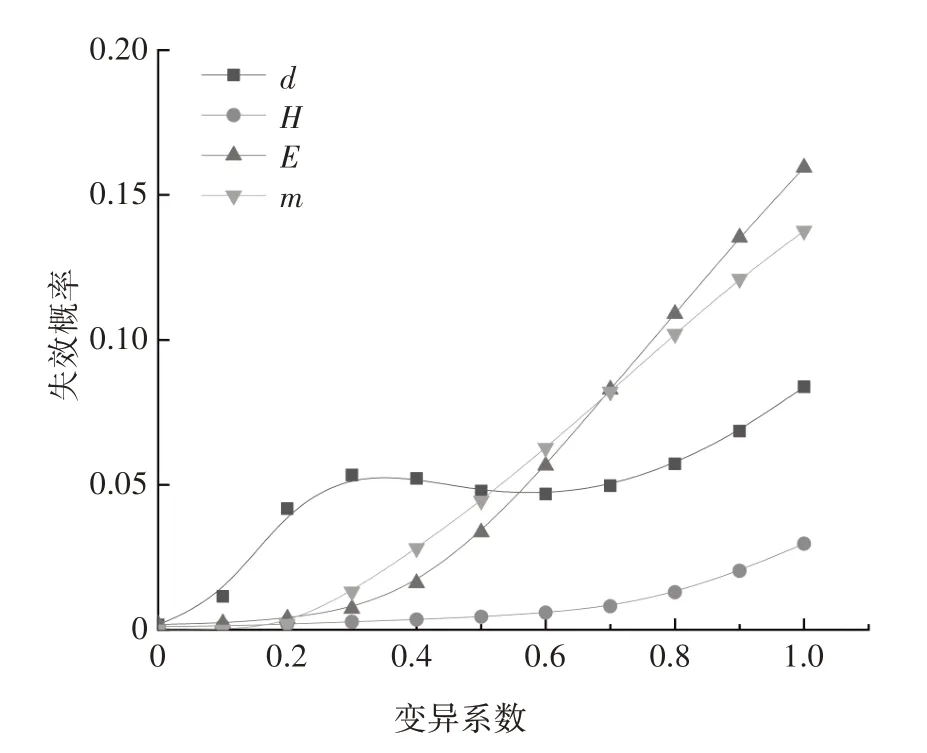
图4 材料屈服失效下变异系数对失效概率的影响Fig.4 Influence of variation coefficient on failure probability under material yield failure

由图3和图4可以看出，在水平位移和材料屈服两种失效模式下，基桩失效概率均随变异系数增大而增大.在水平位移失效模式下，参数变异性对基桩失效概率的影响大小依次为d、H、E和m.当变异系数为0～0.6 范围内时，d、E及m对应的失效概率均随变异系数近似呈非线性关系增加；而当桩径变异系数大于0.6 后，d、E及m对应的失效概率几乎保持不变，即对应的参数变异性对基桩可靠性的影响不明显.在材料屈服失效模式下，基桩失效概率受参数变异性的影响大小依次为E、m、d和H.当桩径d和横向荷载H的变异系数均匀增加时，对应的基桩失效概率几乎不再随变异系数增加而有显著增大.综上可知，参数不确定性对基桩可靠性有较大影响，基桩水平位移失效主要受桩径d和桩顶水平荷载H控制，而桩身材料屈服失效主要受桩身弹性模量E和地基抗力比例系数m控制.

3.4 斜坡效应对基桩失效概率的影响

考虑桩顶水平位移和材料屈服两种失效模式下的容许值［S］，可进一步分析斜坡效应（斜坡效应折减系数η=3、η=4 和η=5）对基桩水平承载可靠性的影响，相应失效模式的容许值［S］与基桩失效概率间的关系曲线如图5和图6所示.

由图5和图6可知，两种失效模式下基桩水平承载失效概率均随容许值［S］增大而减小.在相同的容许值［S］和失效模式下，若不考虑斜坡效应的影响，即不对l1深度范围内地基抗力比例系数m值进行折减而按平地桩计算斜坡基桩的桩身内力与位移，由此得到的基桩失效概率均比考虑斜坡效应（对l1深度范围内地基抗力比例系数m值进行折减）的小.

图5 水平位移失效下的失效概率Fig.5 Failure probability under horizontal displacement

图6 材料屈服失效下的失效概率Fig.6 Failure probability under material yield

图5 显示，在水平位移失效模式下，当桩顶容许位移值［S］介于3.0～4.5 mm 之间时，考虑与不考虑斜坡效应对基桩失效概率的影响比较大，如：当［S］=3.5 mm 时，考虑斜坡效应（η=5）与不考虑斜坡效应（η=0）对应的基桩失效概率差值为0.84.在相同的容许值下，基桩失效概率随折减系数增加而增大.图6显示，在桩身材料屈服失效模式下，斜坡效应对基桩可靠性的影响较小，在相同的桩身材料容许弯矩下，基桩失效概率差值均小于0.12.可见，在水平位移失效模式下，斜坡效应对基桩水平承载可靠性影响较大，尤其是对变形较敏感的高墩桥梁基桩，忽略斜坡效应极有可能给基桩带来安全隐患.

3.5 斜坡效应对基桩安全余量的影响

为探讨斜坡效应对安全余量Z频数分布的影响，根据极限状态函数中随机向量U的分布类型，抽取4×104组服从标准正态分布的随机向量U，分别代入极限状态函数表达式，得4×104组安全余量Z，相应失效模式下其频数分布曲线如图7和图8所示.

由图7和图8可知，水平位移安全余量频数分布受斜坡效应的影响较大，而桩身弯矩安全余量频数分布则受斜坡效应的影响较小.在水平位移失效模式下，对比考虑斜坡效应（η=5）与不考虑斜坡效应（η=0）的PDF 曲线，其峰值对应的安全余量差值为1.3 mm，考虑斜坡效应时，基桩安全余量随斜坡效应折减系数增加而减小；对比两条CDF曲线发现，不考虑斜坡效应会导致位移安全余量更多地集中在较大区域，基桩失效概率明显偏小.类似地，在桩身材料屈服失效模式下，基桩PDF 曲线和CDF 曲线发展规律接近，斜坡效应对基桩失效概率的影响较小.总之，基于随机响应面法得到的极限状态函数，其安全余量频数分布规律与前述结论相符，再次验证理论模型及求解方法的合理性.

4 结论

根据斜坡段桥梁基桩的承载特性，导得了基桩内力与位移计算的有限差分解答；基于桩身水平位移和材料屈服两种失效模式，将随机响应面法与基桩水平承载可靠性分析相结合，并编制了相应的计算程序；据此结合工程实例，进一步分析了地基抗力比例系数、水平荷载、桩身弹性模量及桩径等参数的变异性、斜坡效应对基桩水平承载可靠性的影响，得到的主要结论如下.

1）分别利用蒙特卡罗法（MCS）、二次函数响应面法（RSM）和随机响应面法（SRSM）求解斜坡基桩水平承载可靠度指标和失效概率，验证了随机响应面法及计算程序的合理性.

2）参数变异系数越大，基桩水平承载可靠性越差.在水平位移失效模式下，基桩失效概率随桩径、地基抗力比例系数及桩身弹性模量的变异系数先增大而后趋于稳定，相对而言，桩径对基桩水平承载可靠性的影响最大.而在材料屈服失效模式下，当变异系数小于0.3 时，桩径的影响最大；当变异系数大于0.3 后，桩身弹性模量和地基抗力比例系数对失效概率的影响更显著.

3）斜坡效应对水平位移失效模式下基桩可靠性影响较大，当桩顶容许位移为3.5 mm时，考虑与不考虑斜坡效应对应的基桩失效概率差达0.84，基桩失效概率随斜坡效应折减系数增加而增大；若不考虑斜坡效应，基桩位移安全余量会集中在较大区域，从而导致基桩失效概率偏小.相对而言，斜坡效应对材料屈服失效模式下基桩水平承载可靠性的影响较小.对变形较敏感的高墩桥梁基桩，忽略斜坡效应极有可能给基桩设计带来安全隐患.