考虑地层空间变异性的岩溶区基础可靠度分析

吴高桥，聂建国

（清华大学土木工程系，北京 100084）

我国喀斯特地貌占地约344 万平方千米，广泛分布于我国西部地区.随着近年城市化进程加速，土地紧缺问题日益严重，因此越来越多建筑将无可避免地选址在岩溶发育地区.然而近年来，因地层中空洞失稳引起的上部构筑物沉降和倾斜等灾害时有发生，据2020 年中央级媒体、部委网站、公开出版物、中央重点新闻网站及地方重点报网等报道的数据，2020 年地下空洞相关灾害与事故共237 起，数量与2019 年持平［1］，造成巨大的人员伤亡和经济损失.因此，对含溶洞地层上基础的可靠性进行分析，将有利于上部构筑物的安全性，并为上部施工提供指导，具备重要理论意义和实际工程价值.

国内外有众多学者通过理论分析、模型试验和数值模拟等手段针对空洞-基础体系稳定性开展研究.在理论分析方面，Wang 和Hsieh［2］基于传统上限分析法研究了圆形空洞正上方条形基础的稳定性问题，提出基础稳定性理论计算框架和基础极限承载力计算公式，并总结3 种典型破坏模式.随后Wang等［3］继续研究了空洞与条形基础水平距离对体系破坏模式的影响，将典型破坏模式扩展至10 种，并归纳了不同破坏模式之间的演化规律.刘辉等［4］通过极限分析上限法合理构造速度场，进而通过剪切耗散和基础功率的关系推出溶洞上方条形基础的极限承载力计算方法，并详细分析了不同参数对体系破坏模式的影响.赵明华等［5］考虑自然溶洞形成过程中溶洞顶板的空间形态特征，采用结构力学分析理论建立了溶洞顶板最小抗弯厚度的计算公式，并揭示了该厚度随空洞跨度、地层物理力学性质以及基础所受荷载改变而变化的规律.在模型试验方面，Wood 等［6］和Al-Tabbaa 等［7］基于模型试验分析了下伏空洞对上部浅基础承载力的削弱作用.Kiyosumi等［8］研究了溶洞-基础体系的稳定性问题，通过对基础失去承载能力后溶洞周边岩体的破坏情况，总结了多溶洞工况下，不同排布位置的溶洞对上部基础极限承载力的影响.刘铁雄等［9］和王革立［10］将溶洞上方地层视为梁板，通过一系列试验分析了溶洞跨径、溶洞上覆岩土体厚度等对基础稳定性的影响.赵明华等［11］通过模型试验，研究了上部基础荷载作用下的岩溶顶板的承载机理，对诸如顶板厚跨比、地层力学性能等参数开展了参数分析，并总结了溶洞安全埋深的计算公式.

上述研究使研究工程人员对空洞-基础稳定性问题有了更深入的认知，但使用理论分析时，通常要事先对问题进行一定假设以降低求解难度，因此仅能分析相对简单的问题.而模型试验受限于时间成本和经济成本，无法开展大规模研究以进行参数分析.随着计算机算力的发展，数值模拟成为了一种被广 泛 使 用 的 岩 土 工 程 分 析 方 法.Baus 和Wang［12］在1983 年采用有限元法（finite element method，FEM）研究了粉质黏土中空洞上方条形基础的稳定性问题，并总结出能够反映空洞尺寸、空洞位置及条形基础埋深对基础极限承载力影响的设计图.Badie 和Wang［13］采用三维有限元程序对基础-空洞体系稳定性进行分析，结果表明基础下方存在某临界区域，只有当下伏空洞处于该区域范围内时空洞才会对基础造成显著影响，且该临界区域的范围取决于土体物理力学性质以及空洞大小和位置.Jao 等［14］使用有限元法研究了条形基础荷载作用下的有衬砌隧道稳定性问题，对不同地层类型、隧道大小、隧道位置以及衬砌厚度的影响进行了详细探讨.孙映霞等［15］采用有限差分法（finite difference method，FDM）研究下伏空洞埋深以及距基础距离对体系失稳机理的影响.随后在其基础上，Kiyosumi 等［16］使用有限元软件PLAXIS 率先对多空洞上方条形基础的极限承载力进行研究，分析了不同位置空洞对基础造成影响强弱的关系，结果表明靠近基础的空洞对基础承载力造成的影响远大于较远处空洞.基于Kiyosumi 的研究，Lavasan 等［17］分析了位于两个平行圆形空洞上方的条形基础的极限承载力，深入研究了空洞的破坏机理并归纳了数种典型破坏模式.随后Zhou 等［18］和Lee 等［19］分别采用局部不连续优化法（discontinuity layout optimization，DLO）和有限元法分析了下伏双空洞对条形基础稳定性的影响.

上述研究基本全部假设空洞所处地层为均匀材质，然而现实中地层往往具有一定的空间变异性，这将导致基础承载机理发生改变，进而增加基础承载力的不确定性，因此有必要在基础稳定性分析中充分考虑土体空间变异性的影响.鉴于此，本研究结合随机场理论和Karhunen-Loeve 展开构造实现随机场土体强度的随机分布，进而通过有限元极限分析和蒙特卡洛模拟（Monte Carlo simulation）对含溶洞地层上基础进行可靠度分析，着重分析下伏溶洞位置及土体空间变异程度对基础稳定性及失效概率的影响，以期为工程设计提供参考，并进一步确保岩溶区基础的安全性.

1 问题描述

1.1 基本假定

图1 为待研究问题的平面模型示意图，问题关键影响因素已标示于图中.具体为：地表存在宽度为D的条形基础，在其中心位置施加有竖直集中荷载qu.基础下方地层存在边长为D的正方形溶洞，溶洞中心到地表及基础中垂线的垂直距离分别为H和S.空洞周围的土体遵循特雷斯卡屈服准则（Tresca yield criterion）且存在一定空间变异性，其重度γ=20 kN/m3，平均剪切强度su=40 kPa.

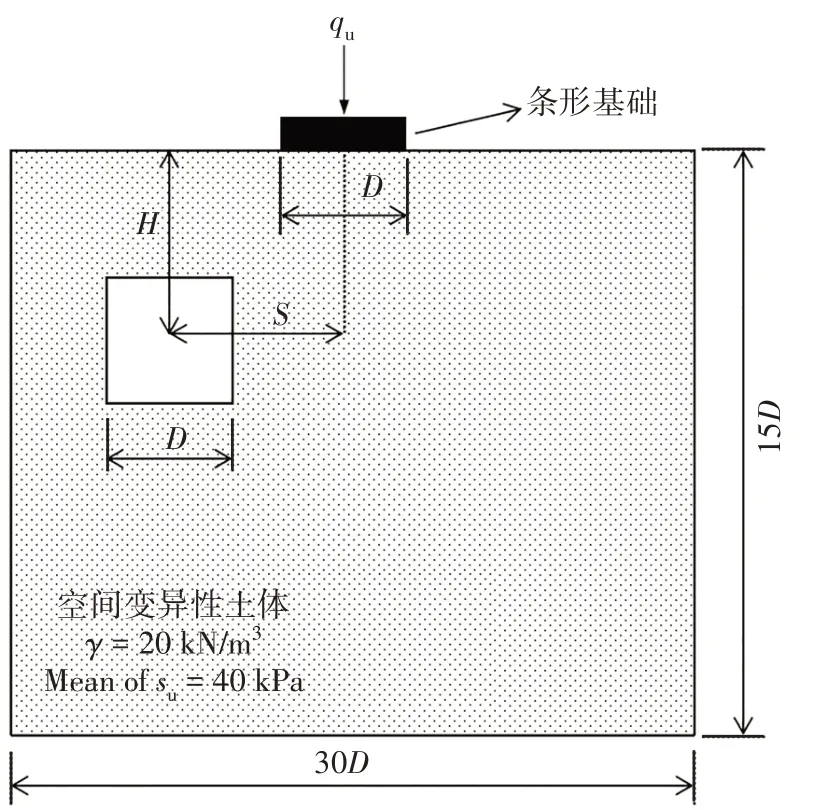
图1 平面模型示意图Fig.1 Sketch of plain strain model

1.2 数值模型建立

为了尽量规避边界效应，需要建立尺寸足够大的数值模型，以保证在所有工况中塑性破坏区不会延伸至模型的侧面边界以及下边界.经测试，当模型尺寸宽度为30D、高度为15D时既可满足上述要求，也能保证较高的运算效率.此外，基于已有研究［19-21］，本文在模型底部边界设置完全约束，左右两侧边界设置水平约束，在地表边界则不设置约束.由于本文拟采用蒙特卡洛法分析基础失效概率，所以对每组工况均需开展上千次模拟以获得准确结果，这将耗费大量时间.因此为了尽可能提高分析效率和精度，采用网格自适应迭代技术基于分析域内能量耗散情况对网格进行重分布优化.针对本文数值模型，将网格初始数量和最终数量分别设置为1 000和10 000，自适应迭代次数设为3 次，经过重分布优化后的效果图如图2所示.

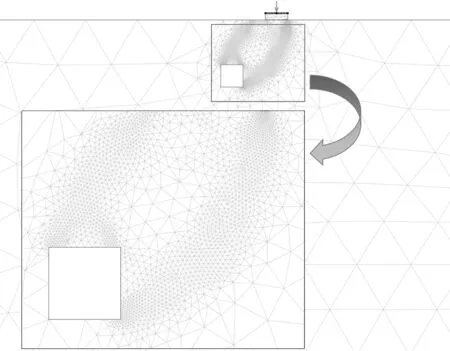
图2 网格自适应分布效果图Fig.2 Sketch of mesh re-arrangement

1.3 随机场实现

本文假定地层土体遵循Tresca 屈服准则，其中对基础稳定性影响最大的参数为不排水剪切强度su，因此在本文的随机分析中主要考虑土体剪切强度的空间变异性.为实现土体空间变异性，将土体不排水剪切强度在分析域内模拟为对数正态分布，其具体表达式为：

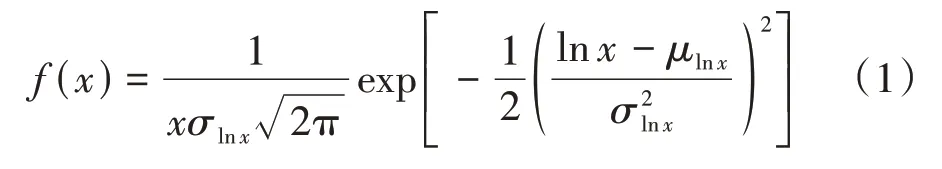
剪切强度的均值和标准差可以通过一种能简洁描述随机场土壤固有变异性的无量纲变异系数（coefficient of variation，COV）表示.该参数能够帮助设计者对土体中固有变异性的可能范围进行评估［22］，具体表达式为：

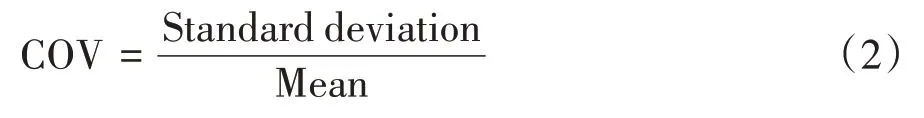
上述表达式中的对数正态分布参数可表示如下：

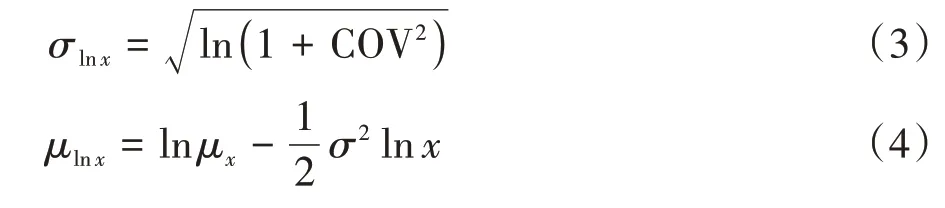
对式（3）和式（4）进行转换可得：

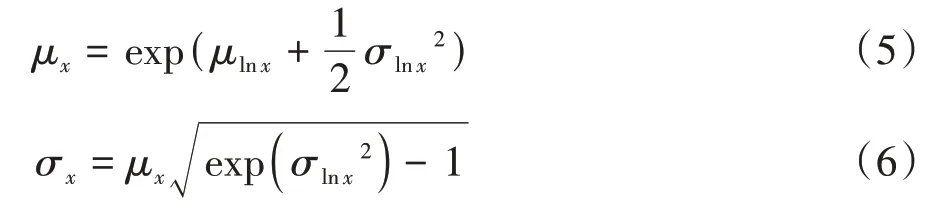
则对数正态分布的累积分布函数（cumulative distribution function，CDF）可表示为：

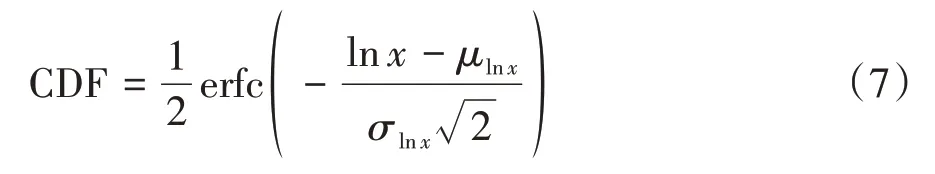
式中：erfc为互补误差函数.需要注意的是，CDF是随机分析中概率密度函数（probability density function，PDF）的积分形式.

除了上述对数正态分布参数，还有两个重要参数在随机场理论中至关重要，即用于描述空间变异性土体不同方向波动程度的水平相关长度（CLx）以及垂直相关长度（CLy）.相关长度被定义为土体中一临界距离，若土体中任意两点间距离小于该距离，则两点的剪切强度趋于密切相关，且相关长度越大则随机场中剪切强度的过渡越平滑；相反，相关长度越小则土体中各点剪切强度的关联性越弱，随机场趋于参差.由其定义可知当相关长度趋于无穷大时，分析域可视为均匀土体；而当其趋于0 时，随机场中各点之间无任何关联.为了更直观地反映相关长度与随机场平滑度的关系，将水平、竖直相关长度不同的土体剪切强度分布模拟情况列于图3.对比图3（a）和图3（b）可以看出，当竖直相关长度较大时，土体剪切强度在竖直方向过渡较均匀；而当水平相关长度较大时，则土体剪切强度在水平方向过渡较均匀.由图3（c）可知若各向相关长度均较小，土体的剪切强度分布较离散且无规律.Phoon 和Kulhawy［22］经过大量调研总结出土体在水平方向的随机性通常较弱，CLx范围在46 m 到60 m 之间；而土体在竖直方向的随机性通常较强，CLy的范围在0.8 m 到6.1 m 之间.基于上述结论，本文中的CLx固定为50 m，仅考虑CLy对基础稳定性的影响.为了方便表述，对相关长度进行无量纲化处理如下：

图3 不同相关长度对应的土体剪切强度分布云图Fig.3 Shear strength distribution of soil domain with different correlation lengths

本研究选择通过能够提供指数协方差函数解析解的Karhunen-Loeve 展开式生成随机场.由于该展开式的项数将随着随机场相关长度的减小而大幅增加［23］，因此为了保证随机分析结果的可靠度，将展开项数设置为1 000.此外，本研究采用蒙特卡洛模拟分析基础失效概率，若模拟次数不足，将严重影响所得结果的准确性，因此在后续随机分析中各工况模拟次数均设为500次.

2 确定分析

通过随机分析研究基础失效概率问题的原理是先不考虑土体空间变异性，对各工况进行传统确定分析（deterministic analysis）；随后再通过多次模拟随机场并总结小于经安全系数换算过的确定性分析基础承载力的次数，进而得出基础失效概率.则失效概率的表达式为：

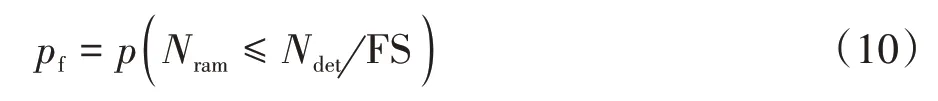
式中：pf为基础失效概率，在本文中具体定义为500次蒙特卡洛模拟所得极限承载力中小于确定性承载力Ndet与安全系数比值的比例；FS为设计中选取的安全系数（factor of safety），一般来说安全系数越大，则设计越保守；Nram为每次蒙特卡洛模拟所得基础极限承载力因子；Ndet为确定分析中的基础极限承载力因子，其具体定义为：

式中：qu为基础极限承载力；su为土体剪切强度.

基础极限承载力与下伏空洞所处位置密切相关，参照已有研究，在本节中对H/D=1、2、3、4 以及S/D=0、0.5、1、2、3、4 对应的工况进行确定分析，所得结果为上限解及下限解的平均值，基础极限承载力因子总结于图4 以及表1.由图4 可知基础极限承载力将随着S/D以及H/D的增加而提升，这是因为下伏溶洞离基础越远，则其对基础造成的负面影响越弱.同时，H/D越大则对应的承载力曲线越平缓，这说明溶洞埋深越大则水平位置的改变对基础的影响越弱.此外，图4 中有多个工况基础极限承载力因子集中在5.20 附近，该现象说明此时溶洞由于距离过远不再对基础产生影响.

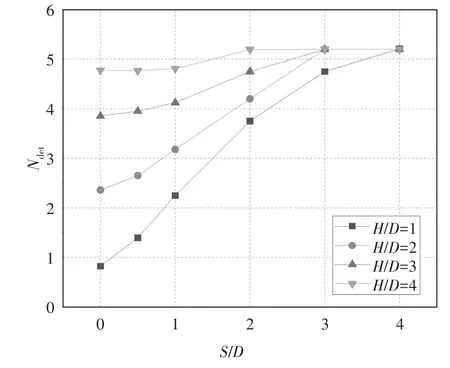
图4 不同H/D条件下S/D对Ndet的影响Fig.4 Effect of S/D on Ndet with different H/D

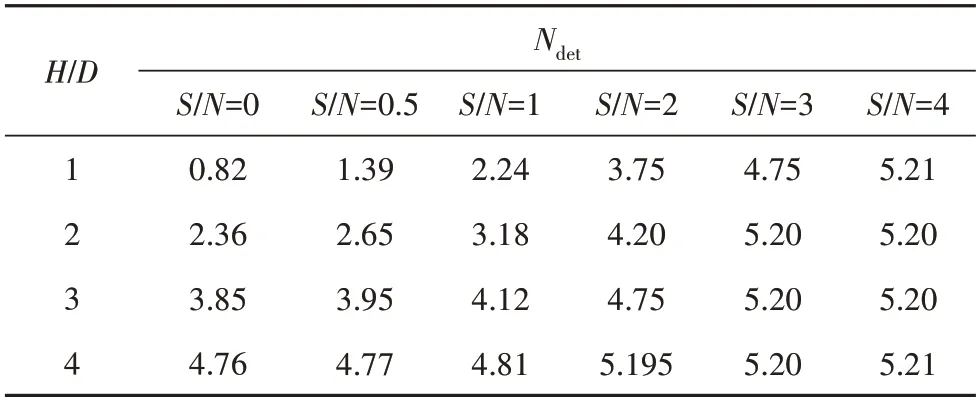
表1 H/D和S/D对Ndet的影响Tab.1 Effect of H/D and S/D on Ndet

3 随机分析

本节将基于确定性分析结果开展随机分析，以期全面探究空洞埋深、空洞水平偏移距离以及土体竖直相关长度对基础平均承载力因子以及失效概率的影响.其中基础平均承载力因子为每个工况500次蒙特卡洛模拟所得极限承载力因子的平均值.由于随机分析中每个工况均需构造500 个不同的随机场并计算相应的基础极限承载力，导致运算量巨大，因此对所有影响因素进行排列组合再开展全面分析是不现实的.鉴于此，本文参考正交试验设计原理，在探究某些参数的影响时固定其他参数，以达到减少运算量且不影响所得规律的目的.本文随机分析所考虑工况的具体参数见表2.

表2 待研究影响因素Tab.2 Influential factors to be investigated

3.1 空洞埋深的影响

为了探究空洞埋深对基础稳定性的影响，对S/D=0，Θy=1以及H/D=1，2，3，4对应工况开展蒙特卡洛模拟，所得基础平均极限承载力因子和失效概率分别总结于图5 和图6.由图5 可以看出随机分析所得的平均承载力因子变化趋势基本和确定分析一致，但由于土体存在空间变异性，导致蒙特卡洛模拟所得的大部分基础极限承载力因子小于确定分析，所以平均承载力因子会小于确定分析所得结果.

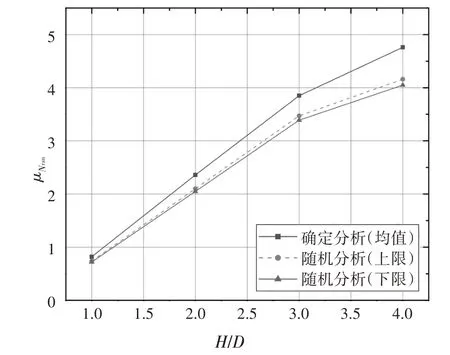
图5 S/D=0，Θy=1，COV=25%时H/D对μNram的影响Fig.5 Effect of H/D on μNram with S/D=0，Θy=1，COV=25%

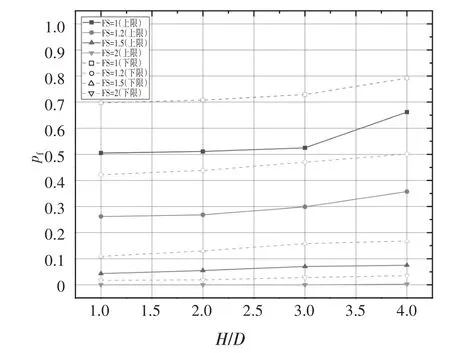
图6 S/D=0，Θy=1，COV=25%时H/D对pf的影响Fig.6 Effect of H/D on pf with S/D=0，Θy=1，COV=25%

图6 为各工况通过上、下限分析所得的基础失效概率.可以看到对几乎所有工况而言，基础失效概率都随空洞埋深的增加而增加，该结论似乎与实际情况不符，因为通常认为下伏溶洞距离基础越远则其对基础承载能力造成的负面影响越小.实际上确如图5所示，基础的极限承载力因子随着H/D的增加而单调增加.但本文中的失效概率是指采用确定分析所得基础极限承载力进行设计时，由土体空间变异性引起失稳的概率，与基础极限承载力的绝对大小无必然联系.值得一提的是，在实际工程设计中一般会通过增加安全系数的方式以保证安全性，因此有必要在失效概率分析中考虑安全系数的影响.由图6 可以看出随着安全系数的增加，基础失效概率显著下降，当安全系数为2 时基础的失效概率将趋于0，同时由曲线上升幅度可知安全系数越小则空洞埋深对基础失效概率的影响越显著.此外，通过对比上、下限分析对应的失效概率，可以看出使用上限分析进行蒙特卡洛模拟时所得基础失效概率较低.为了进一步探究基础失效概率变化机理，将某次蒙特卡洛模拟所得溶洞-基础体系破坏模式总结于图7，可以看出当空洞埋深较浅时，破坏线较集中，说明体系的破坏模式较单一.而随着溶洞埋深的增加，主破坏线逐渐向周围发散且发散程度越来越明显，而这些较为发散的破坏线可能导致土体中失稳路径（failure path）增加，进而引起破坏模式的复杂化并导致失效概率的增加.

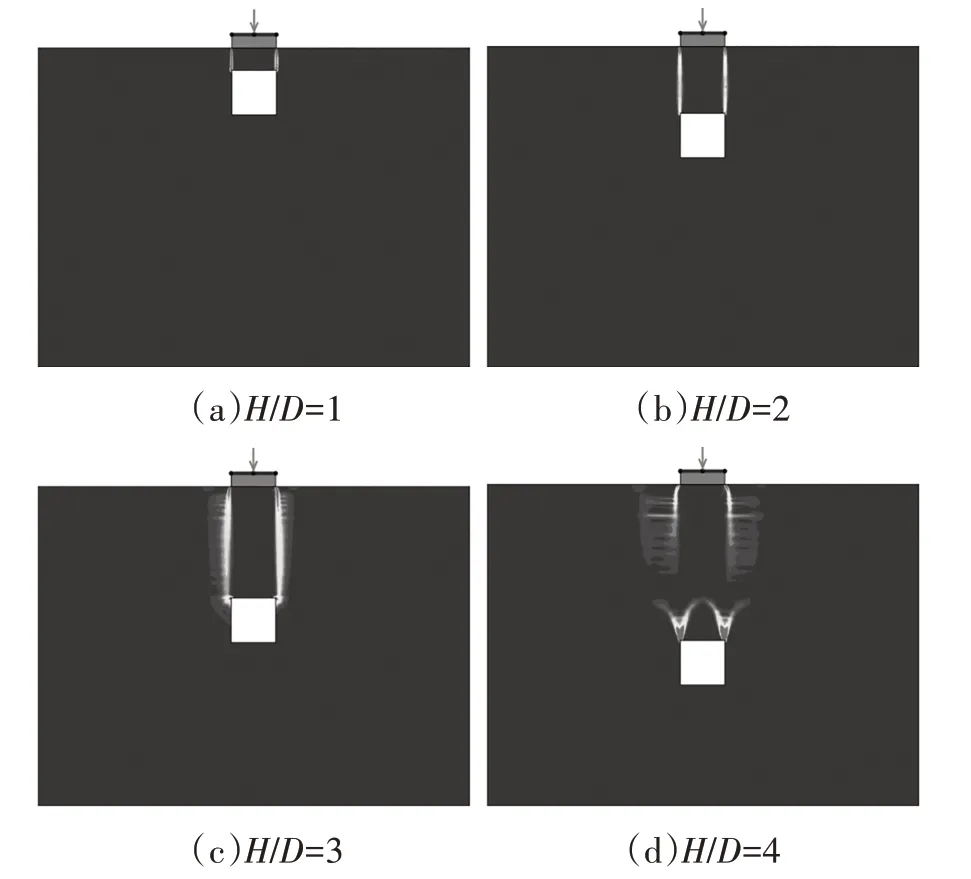
图7 S/D=0，Θy=1，COV=25%时H/D对体系破坏模式的影响Fig.7 Effect of H/D on failure pattern with S/D=0，Θy=1，COV=25%

3.2 空洞水平偏移距离的影响

为了探究空洞水平偏移距离的影响，将H/D=2，Θy=1 以及S/D=0.5，1，2，3，4 工况对应的平均承载力因子和基础失效概率总结于图8 和图9.由图8 可以看出随机分析所得的平均承载力因子变化趋势与确定分析基本一致，这与图5 所展示的规律基本一致.由此可以认为只要蒙特卡洛模拟次数达到一定数量，那么土体空间变异性几乎不会对随机分析中的平均承载力因子变化趋势造成影响.

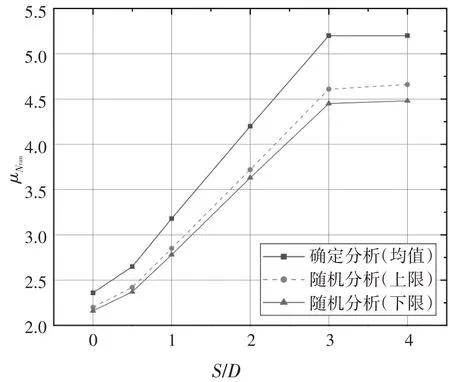
图8 H/D=2，Θy=1，COV=25%时S/D对μNram的影响Fig.8 Effect of S/D on μNram with H/D=2，Θy=1，COV=25%

从图9可看出除FS=1的下限分析以及FS=1.5的上限分析在S/D=0 时失效概率略高于S/D=0.5，其余工况的基础失效概率随溶洞水平偏移距离的增加而增加.图10 为各工况对应的体系破坏模式，可以看出当溶洞水平偏移距离较小时，破坏主要集中在洞顶，且破坏线较细.随着空洞偏移距离的持续增加，破坏模式逐渐变为洞顶-洞侧联合破坏，且溶洞顶部将受到来自其正上方土体的挤压.此外可以看到S/D=0 和S/D=0.5 时破坏线离散度较低，因此其所对应的失效概率接近.而随着溶洞水平偏移距离的增加，破坏线发散程度加剧进而导致基础受荷时土体中可能发展出的失稳路径增多，引起失效概率的增加，这与图9 所展示的规律相吻合.结合3.1 与3.2 节的研究，可以认为对大部分工况而言，除了溶洞水平偏移距离极小的工况，下伏溶洞与基础的间距（包括埋深及水平偏移距离）越大，则对应的基础失效概率越高.此外结合图6和图9可知采用极限分析下限法进行随机分析时，所得基础失效概率相对于上限法明显偏高，而承载力偏低，亦即采用下限法进行施工设计时总体偏于保守.

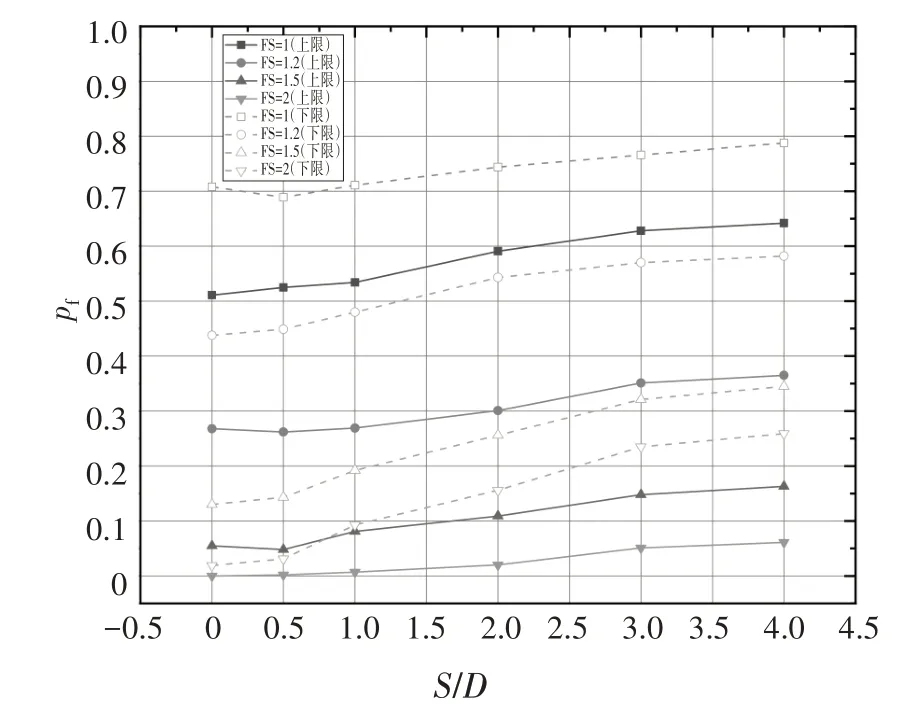
图9 H/D=2，Θy=1，COV=25%时S/D对pf的影响Fig.9 Effect of S/D on Pf with H/D=2，Θy=1，COV=25%

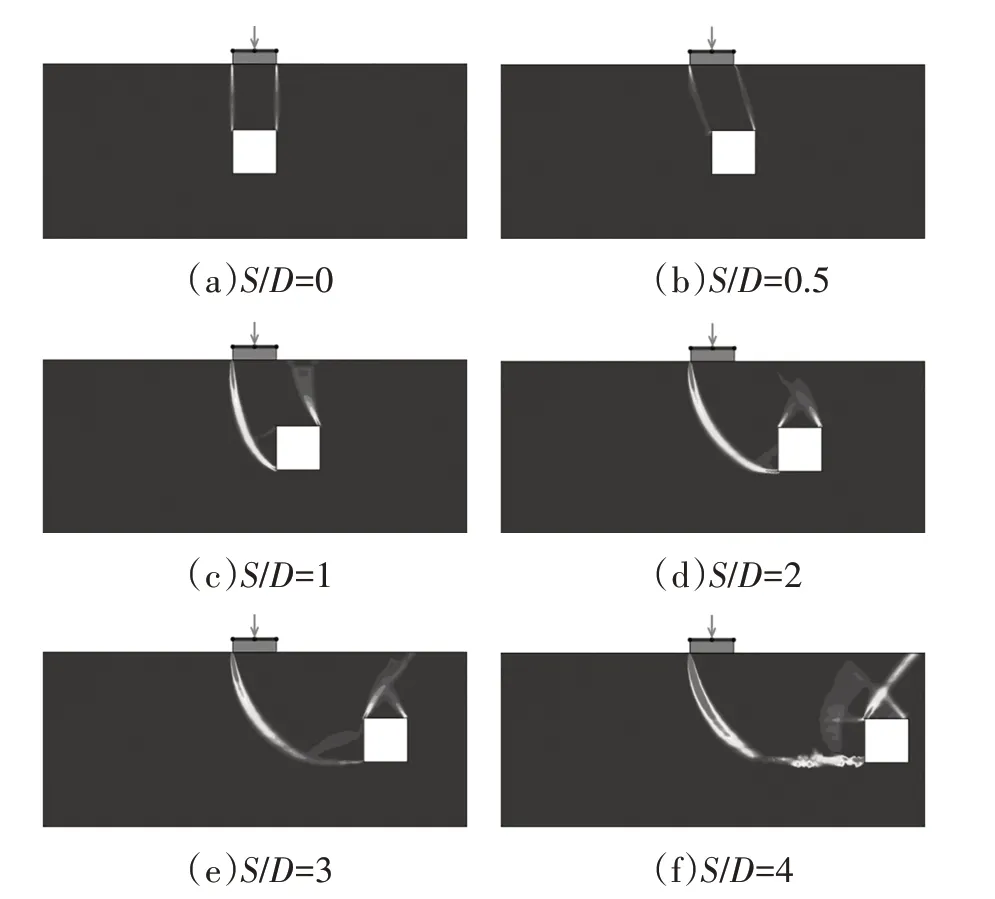
图10 H/D=2，Θy=1，COV=25%时S/D对体系破坏模式的影响Fig.10 Effect of S/D on failure pattern with H/D=2，Θy=1，COV=25%

3.3 土体空间变异性参数的影响

为了探究土体空间变异性参数对基础稳定性的影响，在本节对H/D=2、S/D=1 时不同Θy和COV 对应的基础平均承载力因子和失效概率进行分析.由图11可知基础平均承载力因子随竖直相关长度的增加而单调递增，这是因为土体强度相关性越高则地层中剪切强度的过渡更平滑，从而使得由于土体强度分布不均导致的极低承载力工况数量减少.且承载力增强速度将逐渐平缓，当Θy=4 时平均承载力因子已与确定性分析所得结果（图中水平虚线所示）相差无几，这说明此时土体空间变异性的影响较弱，已趋近于均质土.此外，COV 越大则平均承载力越低，这是因为土体变异系数越大则土体空间变异性越强，这将导致蒙特卡洛模拟中低承载力工况数量的增多，进而引起平均承载力因子的下降.

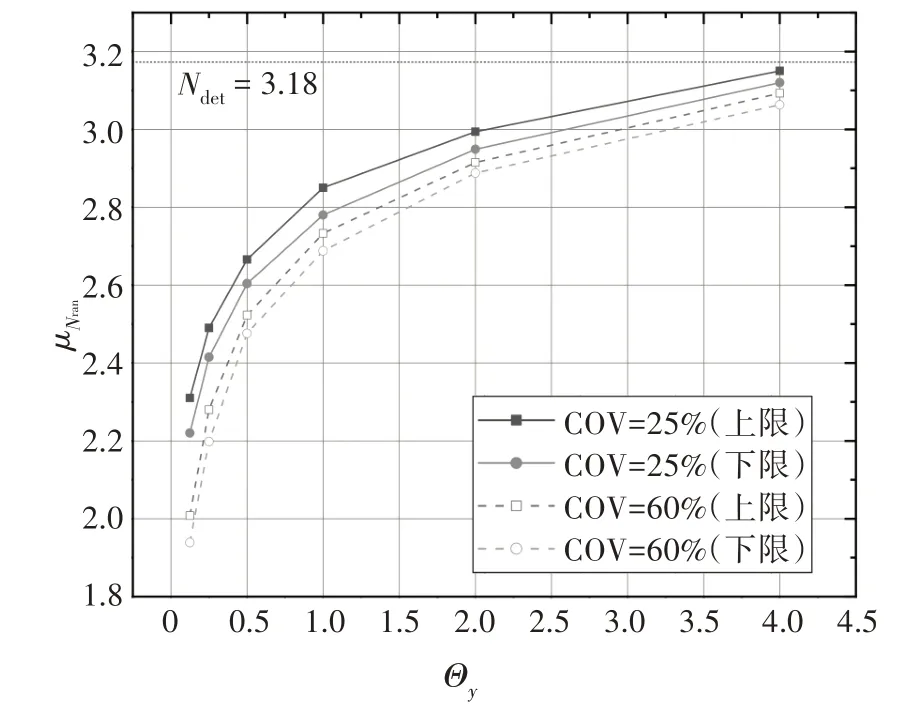
图11 H/D=2，S/D=1时Θy对μNram的影响Fig.11 Effect of Θy on μNram with H/D=2，S/D=1

图12为Θy和COV对基础失效概率的影响.可以看到失效概率随Θy的增加而单调递减，且当Θy很小时，失效概率相对很高，此时Θy只需略作提高则基础失效概率将大幅降低，而随着Θy的进一步增加，失效概率的降低速度减缓.结合上文所得结论，可知空间变异性较强时，空间变异性参数对基础承载力以及失效概率的影响较显著，而当空间变异性较弱时，空间变异性参数的改变仅对基础产生微弱影响.

图13为不同Θy和COV对应的破坏模式图.对比图13（a）（c）（e）（g）和图13（b）（d）（f）（h）可以看到当Θy较小时，破坏线的离散度很高，因此所对应的基础失效概率很高；而当Θy从2 增加到4 时，体系破坏模式及破坏线几乎没有变化，说明此时基础失效概率趋于稳定，与图12 所示规律相吻合.而对比COV=25%（左侧纵列）和COV=60%（右侧纵列）对应的破坏模式，可以看出COV=60%对应的地层空间变异性强度明显高于COV=25%时.以图13（b）为例，在基础和溶洞间的主要破坏线之外还发育有多条破坏路径，这将导致基础失效概率剧增及承载力下降，因此COV 越大则基础失效概率越高，平均承载力因子越低，与图11和图12所示规律一致.

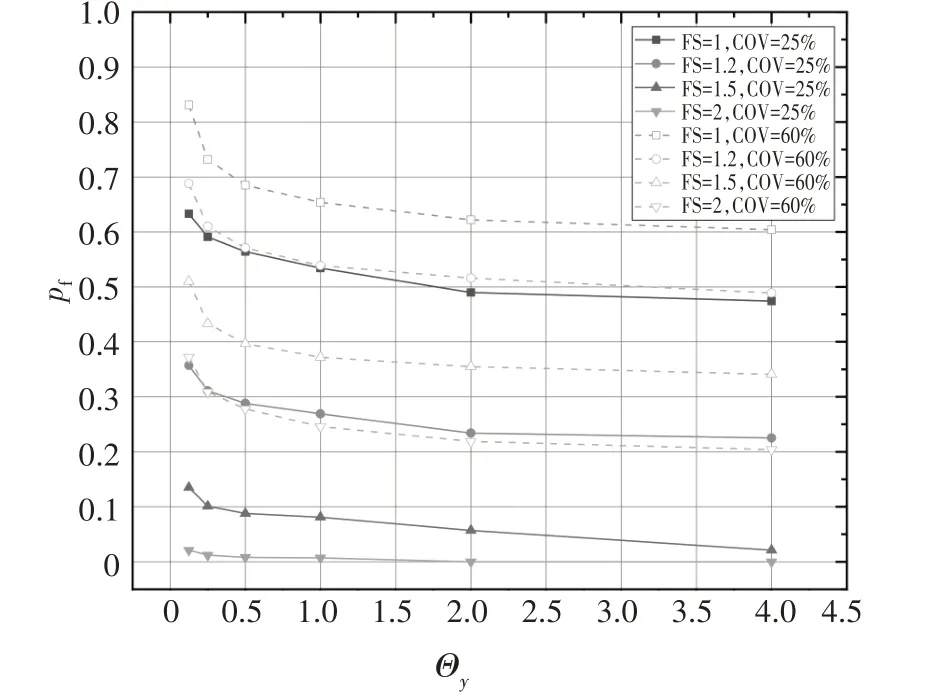
图12 H/D=2，S/D=1时ΘY对pf的影响Fig.12 Effect of Θy on pf with H/D=2，S/D=1

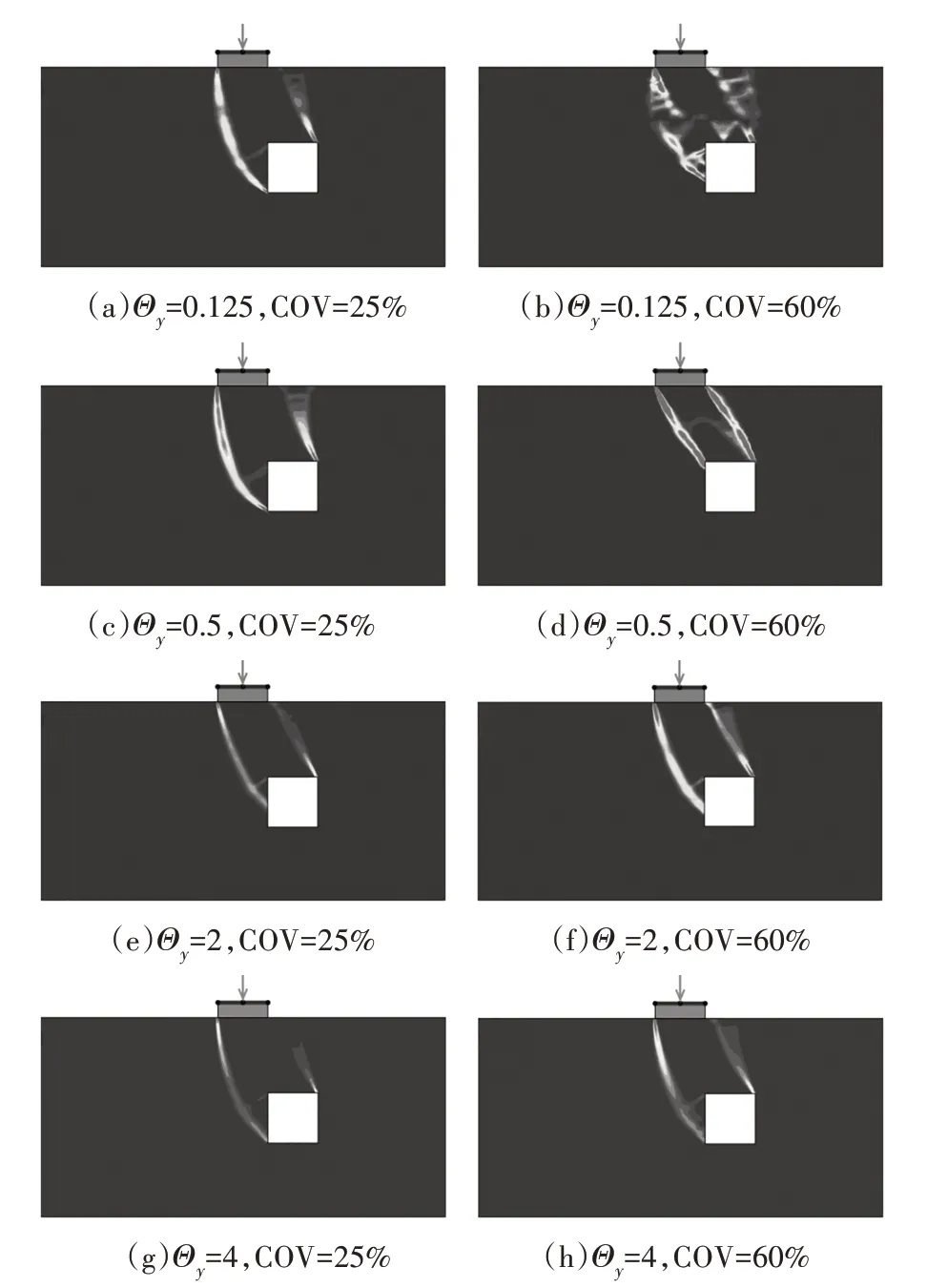
图13 H/D=2，S/D=1时Θy和COV对体系破坏模式的影响Fig.13 Effect of Θy and COV on failure pattern with H/D=2，S/D=1

4 模型验证

为了验证有限元极限分析模型的可靠性，将本文确定分析的结果与已有有限元法［19］和不连续局部优化法结果［18］进行对比，如图14 所示.通过对比可以发现本文上限分析结果略高于已有研究结果，下限分析结果则略低于已有研究结果，但总体变化趋势基本吻合，且最大误差小于5%.此外，有限元极限分析的真值是介于上、下限分析结果之间的，因此可以认为本文数值模型所得结果是准确可靠的.

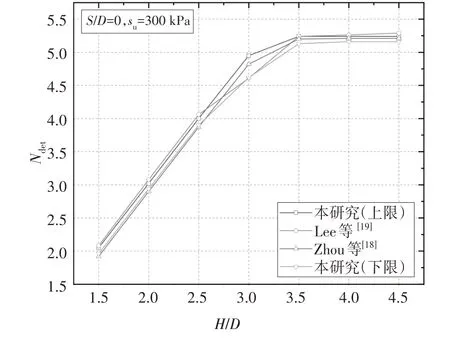
图14 本研究结果与不同数值方法结果对比Fig.14 Comparisons between the present results and results from other numerical methods

5 结论

本文通过随机场理论和Karhunen-Loeve 展开的方式构建随机场，对岩溶发育地层上基础开展了一系列随机分析.采用有限元极限分析法以及蒙特卡洛模拟全面探究了溶洞埋深、溶洞水平偏移距离、土体相关长度以及土体变异系数对基础稳定性以及失效概率的影响，并结合可视化体系破坏模式深入分析基础失效概率变化机理.本研究所得结论如下：

1）在随机分析中，若蒙特卡洛模拟样本数足够，则随机分析所得基础承载力变化趋势与确定分析所得趋势几乎一致；

2）基础的承载力将随溶洞埋深、溶洞偏移距离、土体相关长度的增大以及土体变异系数的减小而提升，且上述参数较小时对基础的影响更显著；

3）溶洞与基础的间距越远，则基础的失效概率越高.且基础的失效概率随土体相关长度的增大而降低、随土体变异系数的增大而升高；

4）在施工设计时采用极限分析下限法对基础稳定性进行随机分析时将偏于保守，所得基础失效概率偏高且极限承载力偏低，且基础失效概率将随所取安全系数的增加而大幅降低；

5）破坏模式中离散度较高的破坏线将导致基础受荷后可能发生破坏的失稳路径增多，从而导致更高的失效概率.